中美股票市场流动性相依结构的动态特征研究
汤 芮
(安徽财经大学 金融学院,安徽 蚌埠 233000)
中美股票市场流动性相依结构的动态特征研究
汤 芮
(安徽财经大学 金融学院,安徽 蚌埠 233000)
金融市场间存在着某种相依结构,并呈现复杂性和加强的趋势,特别在金融市场出现极端情况时,这种加强使得暴涨暴跌在若干金融市场内同时出现。研究采用沪深300与标普500指数的流动性时间序列为样本,利用时变Copula函数研究了中美股票市场的流动性动态相依结构特征。研究结果表明:中美两国股市流动性相依结构较稳定,尾部相关性水平较低;金融危机爆发时,两市总体相关系数波动减小,而尾部相关性轻微增加;相依结构存在明显的“政策效应”,这种效应将减弱相关性水平,但是寿命短暂。
相依结构;Copula函数;政策效应;流动性
流动性是衡量金融市场健康有序的关键标准,是金融市场和众多金融工具生存的前提。随着金融全球化、一体化程度的加深,金融市场间呈现出复杂和日益加强的关联性,这种关联性造成了不同金融市场间的流动性呈现出不同的相依结构。众多的研究结果表明,在金融危机或极端情况中,金融变量间的相关性、特别是尾部相关性显著增强。面对复杂、波动剧烈的全球金融环境,我国的金融市场已不能独善其身,因此,研究我国与主要发达国家金融市场之间的流动性相关结构,对于有效应对外部流动性冲击,合理调控流动性水平,保持我国金融市场健康发展具有重要的现实意义。
金融市场间存在相依结构已被理论界所认可和接受,这种相依结构对资产风险管理具有重要意义,也是理论界研究的热点。胡秋灵和于婷婷(2013)研究了不同时期我国股票市场和债券市场的联动性,发现国内因素对两市场的影响较大,国际因素的影响程度相对有限[1]。朱为玉(2014)从收益率角度,研究了股票市场中与债券收益率高度相关的股票投资组合的特征[2]。范原源(2014)利用DCC-MVGARCH模型实证研究了股票市场和债券市场间收益率的联动关系,发现两市场间的流动仍存在较大的摩擦[3]。杨宝臣和赵亮(2015)研究了我国股票和债券市场流动性之间的溢出效应,表明了两市间存在双向的非线性Granger因果关系[4]。陈学彬和曾裕峰(2016)基于多元分位数研究了中美股票指数和债券指数的尾部风险溢出效应,研究结果表明:我国股票市场和不同债券市场的尾部风险溢出关系完全一致,而美国的企业债和股票的尾部风险溢出关系要明显强于国债[5]。龚玉婷等(2016)从月度宏观和日度微观角度出发,研究了通货膨胀率、货币供给量等一系列因素对股债两市场流动性和相关性的影响[6]。陈九生和周孝华(2017)基于条件在险值,结合单因子MSV模型分析股票市场和ETF市场间的风险溢出效应,发现两市间存在双向溢出效应,但股票市场对ETF市场的影响更强[7]。
早期的相依结构研究主要采用相关系数检验法,如King和Wadhwani(1990)通过分析1987年美国股市崩盘前后相依性水平的变化,发现危机后欧美股市间的联动关系加强[8]。随着上世纪90年代金融市场波动加剧,学者们开始关注金融市场间的动态相依结构,特别是极端情况下的相关性问题。Lai.Y等(2009)采用GJR-GARCH模型进行实证分析,结果显示我国汇率与股票市场间存在不对称的门限协整关系[9]。张兵等(2010)运用Johansen协整检验分析了中美两市是否存在长期均衡关系,并运用分位数回归研究极端条件下市场的联动性[10]。陈云(2013)构建AG-DCC-MVGARCH 模型,实证研究中美股市收益率之间的动态相关性[11]。自从 Copula 函数被引入到金融领域后,便得到了广泛应用,成为研究金融市场相关性的主要方法之一。梁朝晖(2004)利用Copula函数对流动性风险与市场风险的尾部相关关系进行研究[12]。Patton(2006)提出四种时变 Copula模型,进行了两国股票市场动态相关性研究[13]。吴吉林和张二华(2010)运用具有状态转换特征的时变Copula函数,研究了国际金融危机中上海股票市场与美国股票市场之间相关性的变化[14]。Chen和Poon(2011)基于时变 Copula 研究了中国证券市场与国际上其他证券市场之间的相依关系[15]。刘桂梅等(2013)和江红莉等(2013)利用时变Copula函数,研究上证地产股指数和金融股指数收益率的尾部相关性[16-17]。
目前,关于流动性相依结构的文献中,要么围绕流动性和收益率、波动性展开,要么以某一国内的股票与债券、基金市场、现货与期货市场为对象,针对不同国家金融市场间流动相依结构的研究相对较少。笔者认为研究不同国家金融市场间流动性相依结构的意义在于:(1)流动性指标包含价量时空因素,能够综合反映金融市场的活跃性和健康状况;(2)诸如宏观经济走势、调控政策、突发事件等因素将对一国金融市场的流动性产生影响。与研究一国内金融市场不同,这些因素可能只影响本国,也可能影响包括本国在内的若干国家金融市场的流动性。不同国家间的流动性相依结构能够刻画这些因素影响效应的动态特征,有助于分析外部流动性冲击效应和提供金融市场政策调控的决策参考。研究金融市场间相关结构的主要方法为协整分析、格兰杰检验、以GARCH簇为基础的多元相关性模型和copula函数。与copula函数相比,其他方法要么在样本数据中存在非线性、条件异方差或呈现非正态、尖峰、厚尾等性质时检验结果可能出现偏差,要么具有待估参数难以准确估计、假设分布确定等局限性。基于连接技术的时变copula函数,可以较好地刻画金融市场变量间的微观的、动态的非线性关联性和尾部特征,较适应金融市场变量分布难以确定的实际。股票市场是资本市场的核心,也是经济运行的“晴雨表”,对宏观经济走势、调控政策、突发事件等较敏感。考虑到美国的金融地位以及我国的贸易依存结构,本文将采用时变Copula函数研究我国与美国股票市场间流动性的相依结构特征。
一、时变Copula函数
利用时变Copula函数进行相关结构研究的关键在于选择合适的时变Copula函数。本文采用Patton( 2006)提出的时变正态copula(N-Copula)、时变 T-Copula、时变 rotated-Gumbel Copula (RG-Copula)和时变Symmetrized Joe-Clayton Copula(SJC-Copula)作为研究备选的模型。与常数copula的区别是:时变copula函数的参数是动态变化的,而常数copula函数的参数是固定的。因此,时变copula函数能够刻画金融变量的微观、动态特征,尤其是捕捉变量的尾部动态特征。
1.时变N-Copula
N-Copula的分布函数与时变相关系数方程为:
N-Copula:C(u1,u2,…,uN;ρ)=Φp(Φ-1(u1),Φ-1(u2),…,Φ-1(uN))
其中,Φp(·)为标准正态分布,Φ-1(·)为标准正态分布的逆分布;为使ρN,t∈(-1,1),引入修正的Logistic变换Λ(x)=(1-e-x)/(1=e-x)。时变N-Copula适合刻画对称相关性,但是对上、下尾均不敏感,当ρN,t<1时,上下尾相关系数均为零,当ρN,t=1时,下尾相关系数均为1。
2.时变T-Copula
T-Copula的分布函数与时变相关系数方程为:


3.时变RG-Copula
通过对Gumbel-Copula进行变换可以得到RG-Copula的分布函数:
RG-Copula:C(u,v|ρ)=exp(-((-ln(1-u))ρ+(-ln(1-v))ρ)1/ρ)
其中,修正的Logistic 变换Λ'(x)=1+x2使得ρRG,t∈(-1,1)。刻画不对称相依性,对下尾相关敏感而对上尾相关不敏感:λU=2-21/ρ,λL=0,适合研究上行行情中的相关性问题。
4.时变SJC-Copula

其中,CJC为Joe-Clayton Copula的分布函数,方程为:




二、实证分析
1.流动性指标选取与描述性统计分析
在指令驱动市场中,流动性指标主要包括Amihud非流动性指标、Amivest流动性比率和Hui-Heubel流动性比率。由于Amivest流动性比率由股票价格波动与成交量构成,可以消除汇率因素的影响,因此,本文将采用一种修正的Amivest流动性比率作为衡量股票市场流动性的指标。


文本采用沪深300(hs300)和标准普尔500(sp500)指数流动性代表我国与美国股票市场总体流动性,利用Wind数据库获得自2005年1月4日至2012年12月25日的日间数据样本,共 1896 个,数据处理和相关检验采用Matlab2012b。
描述性统计结果如表1所示。hs300与sp500指数流动性序列峰度均高于3,偏度分别为1.4639和1.6780,具有较长的右拖尾,具有显著的尖峰后尾现象。J-B检验结果表明,两个流动性序列不服从正态分布,从图1、2可以明显看出流动性时间序列存在波动聚集的特性,即大的波动之后往往跟随大的波动,反之亦然。ADF检验结果表明,所有序列不存在单位根,都是平稳的。ARCH检验结果表明,滞后10阶,在5%的显著性水平下数流动性时间序列存在条件异方差。lbq检验(Ljung-Box Q)结果显示,两市的流动性序列均存在自相关性。从上述描述性统计结果可以看出,沪深300与标普500指数流动性时间序列具有尖峰后尾、条件异常差、自相关性,故考虑用AR(q)-GARCH模型建模。

表1 hs300与sp500描述性统计特征
注:()表示参数估计伴随的p值

图1 沪深300指数流动性时间序列
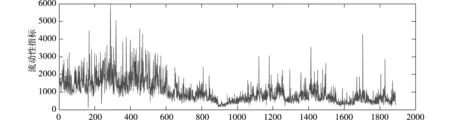
图2 标普500指数流动性时间序列
2.边缘分布建模
根据表1的描述性统计结果,本文选择AR(q)-GARCH(1,1)-N、AR(q)-GARCH(1,1)-T和AR(q)-GARCH(1,1)-SkewT模型分别对liQhs和liQsp建模。
利用matlab2012b,根据AIC信息准则在滞后1-20阶范围内搜索最优滞后阶数,并选择最优拟合的AR(q)-GARCH(1,1)模型进行边缘分布建模。表2的搜索结果表明,在三种AR(q)-GARCH(1,1)模型中,两序列分别在滞后9阶和5阶时AIC准则最优;而在滞后9阶和5阶时AR(q)-GARCH(1,1)-SkewT的AIC准则最优。从分布的性质看,SkewT分布区别于传统的正态分布、学生-t分布,除了具有厚尾特征之外,还引入了偏斜特征。AR(q)-GARCH(1,1)-SkewT模型表述如下:
liQi,t=liQi,t-1,liQi,t-2,…,liQi,t-q)+ei,t
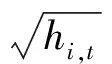


表2 liQhs和lioQsp的AIC值比较
利用matlab2012b分别对AR(9)-GARCH(1,1)-SkewT和AR(5)-GARCH(1,1)-SkewT模型进行参数估计,结果见表3。

表3 AR(q)-GARCH(1,1)-SkewT模型参数估计与检验

β0.8705(0.016)0.8414(0.026)ν5.4217(0.469)5.5775(0.473)λ0.3864(0.029)0.4455(0.033)LL-15543.839-13889.283K-S检验h=0h=0
注:()表示参数估计值的标准差
表3中参数估计结果中,各参数的t统计量均明显大于2,估计结果显著。结合表1和表3统计结果分析,沪深300和标普500指数流动性的自由度较小,均存在明显的厚尾现象,表明我国和美国股市的流动性具有较高的不稳定性。对残差序列进行标准化和概率积分变换并进行K-S检验。检验结果(h=0)不能拒绝原假设,流动性序列残差经过积分变化后服从[0,1]分布,可采用Copula函数进行拟合。
3.时变Copula函数的参数估计
本文分别对时变N-Copula、时变 T-Copula、时变 RG-Copula和时变SJC-Copula进行参数估计,根据AIC 信息准则和对数似然估计选择拟合优度最高的时变Copula模型。见表4。

表4 时变copula参数估计
表4参数结果显示:时变 T-Copula的AIC准则最小,对数似然的值最大,拟合效果最优,时变N-Copula拟合效果次之,但是两者差别较小;时变 RG-Copula和时变SJC-Copula拟合结果较差,两者差别也较小。沪深300与标普500指数的流动性总体和尾部相关性应呈或接近于对称分布。本文将采用时变T-Copula的估计结果对沪深300和标普500指数流动性相关结构进行分析。图3和图4的横坐标从左向右对应的日期分别为:2005年1月、2005年10月、2006年8月、2007年6月、2008年4月、2009年1月、2010年10月、2011年6月、2012年3月、2012年12月。
4.时变相关结构估计结果分析
时变 T-Copula的β参数估计值为-0.3035,表明相关系数之间具有微弱的“矫正”效应,相关系数演化过程表现为较密集的波动性,不存在记忆性,从图3和表5的lbq检验结果(h=1)也可看出。自由度参数DoF较大,值为18.1418,说明沪深300与标普500指数流动性的联合厚尾特征不明显。动态相关系数均值为0.5803,我国与美国股票市场流动性的联动概率水平一般,即一市场流动性变化引起或源于另一市场同方向变化的概率为0.58左右;总体相关系数波动幅度较小(相最高与最低绝对差小于0.1,标准差0.0081),相关结构总体比较稳定。由图3和表5也可看出,总体相关系数分布具有尖峰和左偏尾部特征,演化过程中,相关系数主要在距离均值较近的区域波动,呈现不对称特点,即向下震荡幅度较大(相关性突然减弱)。这种相关性突然减弱主要发生在样本点150-190、650-840和1400附近;而在样本点850至1100区域附近则出现波动减弱。根据样本点与时间对应关系,笔者将深入研究相关系数波动加剧和减小的原因。2005年4月至2005年9月5日《上市公司股权分置改革管理办法》正式出台之前,投资界对股权分置改革持怀疑态度,同期我国股市尚未完全复苏,投资者较多采取观望策略,股市交易低迷,总体流动性较低,波动趋势不明显;同期,美国股市行情较好,连创新高,流动性呈震荡上行态势。因此,这段时期两市流动性相关系数向下震荡较频繁;2005年11月,随着我国迎来大牛市行情后,相关系数波动幅度减弱。2007年5月30日,财政部宣布上调印花税至0.3%,我国股市经历了5.30大跌行情,随后我国股市快速反弹,2007年10月两市市值达到历史最高,随后受美国次级债务、股市频繁再融资以及下调印花税和上调准备金的综合影响,我国股市价格震荡下行,成交量呈现先升后降的趋势。同期美国次级债务危机开始显现,股市价差波动较为剧烈,成交量震荡下降。受政策性因素干扰和次级债务危机共同影响,此期间,两市流动性相关系数波动较大,并出现短暂性减弱。2008年下半年,次级债务危机全面爆发并引发欧债危机,导致世界性经济萧条,我国股市受其影响显著。两市成交量迅速萎缩,流动性下降,相关系数波动显著减小。其后,我国和美国先后发布了4万亿和7000亿刺激经济计划,效果不同的是我国股市反弹明显,而美国股市仍然低迷,流动性相关系数回复平均波动水平。图3中1400样本点附近相关系数出现了最大一次波动,对应时间位置,我们发现 2010年11月12日,双边上调印花税传闻使得我国股市大跌,而同期美国股市较平稳。总体而言,在正常情况下,宏观经济走势对中美两国股市流动性相关系数的影响不明显;极端情况下,总体相关系数波动性减弱,流动性相依结构的稳定性明显增强。一国的政策调控或突发事件对本国股市流动性的影响是显著的,具有明显的“政策效应”,而对别国的影响效果微弱。“政策效应”造成了相关系数的显著减弱,但是寿命明显小于极端情况下宏观经济走势对相关系数的影响。

表5 总体与尾部相关系数特征

图3 总体相关系数演化过程
虽然学术界在关于金融市场收益率相关性的研究中,普遍地认为下尾相关性强于上尾相关性,但是本文的研究表明,我国与美国股票市场流动性上下尾部相关性差异不大。通过表5可知:我国与美国股市流动性尾部相关系数较小均值为0.222,说明两市流动性的同长同跌的概率较低;标准差为0.0478,相关系数波动幅度较总体相关系数为大;峰度和偏度分别为2.7508和-0.2568,不存在明显的尖峰现象,具有轻微的左偏尾部。从图4可以看出,尾部相关性仅表现出微弱的趋势:样本点600之前,轻微的震荡下行;600—1000轻微的震荡上行;1000以后水平震荡。次级债务危机全面爆发之前,我国股市指数处于震荡上升趋势,交易量逐步增加,则流动性指标也是震荡上升,而美国股市则表现出先升后降趋势,成交量下降速度较快,流动性表现出轻微的下降趋势,两者的尾部相关性趋弱。次级债务全面爆发以后,两市场流动性迅速下降,尾部相关系数震荡上升,随后水平波动。较低的相关系数均值和较大的标准差表明:一般情况下,美国股市的流动性主要与美国宏观经济走势有关,而国内外经济环境和存款准备金调整、再融资、印花税率调整等政策性因素是引发我国股票市场流动性升降的主要原因;极端情况下,宏观经济环对两市流动性升降的影响效力增加,但是这种影响产生的相关性增强特征较微弱,可能的原因是国内政策或突发事件对流动性尾部相关性产生干扰。

图4 尾部相关系数演化过程
三、研究结论
本文采用2005年1月至2012年12月沪深300与标普500指数的日流动性数据,利用GARCH、时变copula模型对我国与美国股票市场流动性相关结构进行了研究,得到以下结论:
(1)分别基于时变N-Copula、时变 T-Copula、时变 RG-Copula和时变SJC-Copula函数对沪深300和标普500指数日间流动性时间序列数据进行建模。模型参数估计结果表明:时变T-Copula函数拟合效果最好,两市总体和尾部相关性近似对称分布。总体相关系数均值为0.5803,波动幅度落在[0.5132,0.5934]内,尾部相关性均值为0.222,波动幅度落在[0.0742,0.3488]内。
(2)我国与美国股市流动性总体相关性演化过程表现出波动较密集,波动幅度小的特征,总体相依性强度一般。β参数估计值为-0.3035,具有微弱矫正效应,lbq检验表明不存在显著的自相关,总体相关系数在均值周围上下波动,没有明显趋势形态产生。总体相关系数分布偏度为-0.4021,具有左偏尾部特征,表明相关系数减弱的概率较大。当宏观经济走势出现极端情况时,我国与美国股市流动性相关性结构的稳定性明显加强。一国内的调控政策和突发事件显著影响本国股市的流动性水平,而对别国的影响微弱。影响效果的差异使得“政策效应”将显著地弱化相关性水平,并且这种弱化是短暂的。
(3)参数估计结果表明,我国与美国股市流动性尾部相关性近似对称分布,尾部相关性均值为0.222,两市同时出现流动性急涨急跌的概率较低。政策因素和宏观经济走势是两国股票市场出现极端情况的主要影响因素。不同的是,极端的宏观经济走势将增强尾部相关系数水平;而一国的政策因素或突发事件的“政策效应”将减弱尾部相关性。两种因素的综合作用,使得我国与美国股票市场的尾部相关性结构变化趋势不明显。
以上结论说明,我国与美国股票市场流动性总体相关性结构较稳定,尾部相关性较低。“政策效应”将弱化两国股票市场的流动性相关性水平,但是这种弱化效果时间较短;而极端的经济走势(如次债危机爆发)将减小相关系数波动程度。因此,为了有效应对外部流动性冲击,保持合理的流动性水平,涉及股票市场的调控政策应是长期的,具有一定的连贯性,以弱化我国与其他国家股票市场间的流动性相关性,特别是尾部相关性。
[1]胡秋灵,于婷婷. 我国股票市场与债券市场联动的国内外因素分析[J].上海金融,2013 (1):74-81.
[2]朱为玉. 债券市场和股票市场相关性分析[J]. 金融发展研究,2014 (12):3-11.
[3]范原源. 关于股票市场和债券市场收益率联动特征的研究[D]. 成都:西南财经大学,2014.
[4]杨宝臣,赵亮. 中国股票市场与债券市场间流动性溢出效应的非线性动态特征[J]. 技术经济,2015(9):61-67.
[5]陈学彬,曾裕峰. 中美股票市场和债券市场联动效应的比较研究[J].经济管理, 2016(7):1-13.
[6]龚玉婷,陈强,郑旭. 谁真正影响了股票和债券市场的相关性[J].经济学, 2016(3): 1205-1224.
[7]陈九生,周孝华. 基于单因子MSV-CoVaR模型的金融市场风险溢出度量研究[J]. 中国管理科学, 2017(1): 21-26.
[8]King M A, Wadhwani S. Transmission of volatility between stock markets[J]. Review of Financial studies. 1990, 3(1): 5-33.
[9]Lai Y, Chen C W, Gerlach R. Optimal dynamic hedging via copula-threshold-GARCH models[J]. Mathematics and Computers in Simulation. 2009, 79(8):2609-2624.
[10]张兵,范致镇,李心丹. 中美股票市场的联动性研究[J]. 经济研究, 2010(11): 142-151.
[11]陈云. 中外股市收益率的非对称动态相关性研究[J]. 管理科学,2013(4).
[12]梁朝晖. 上海股票市场流动性风险与市场风险的极值相关分析[J]. 中国地质大学学报 (社会科学版), 2004, 4(8): 49-52
[13]Patton A J. Estimation of multivariate models for time series of possibly different lengths[J]. Journal of applied econometrics. 2006, 21(2): 147-173.
[14]吴吉林,张二华.次贷危机、市场风险与股票市场间相关性[J].北京: 世界经济,2010(3).
[15]Wang K, Chen Y, Huang S. The dynamic dependence between the Chinese market and other international stock markets: A time-varying copula approach[J]. International Review of Economics & Finance. 2011, 20(4): 654-664.
[16]刘桂梅,赵丽. 基于 Copula—GARCH 模型的上证地产股与金融股的相关性研究[J]. 浙江大学学报 (理学版), 2013, 40(2).
[17]江红莉,何建敏,庄亚明. 基于时变 Copula 的房地产业与银行业尾部动态相关性研究[J]. 管理工程学报, 2013(3): 8.
AnalysisofDynamicLiquidityDependenceBetweenChineseandAmericanStockMarket
Tang Rui
(Anhui University of Finance and Economics, Bengbu, Anhui 233000, China)
There are Some dependence structure amoug different financial markets, especially in the case of price fluctu ation. The connection between financial markets both at home and abroad is becoming closer and closer along with the economic integration and globalization. This paper analyzes liquidity dependence between Chinese and American Stock Market based on time-varying copula. The results show that liquidity dependence is stable and tail dependence level is relatively low, the overall fluctuation of correlation coefficient in the two markets reduced and the fluctuation of tail dependence increase slightly in the financial crisis; the dependence structure has obvious ‘policy effects’, which reduced the level of correlation.
dependence; time-varying Copula function; policy effects; liquidity
ClassNo.:F830.91DocumentMark:A
宋瑞斌)
汤芮,学生,安徽财经大学。
2096-3874(2017)12-0087-08
F830.91
A

