基于载荷转移距离和有效宽度的煤柱稳定性评价方法
崔希民,逯 颖,张 兵
(1.中国矿业大学(北京) 地球科学与测绘工程学院,北京 100083; 2.石家庄学院 资源与环境科学学院,河北 石家庄 050035)
基于载荷转移距离和有效宽度的煤柱稳定性评价方法
崔希民1,逯 颖1,张 兵2
(1.中国矿业大学(北京) 地球科学与测绘工程学院,北京 100083; 2.石家庄学院 资源与环境科学学院,河北 石家庄 050035)
煤柱稳定性评价是房柱式开采设计的主要研究内容之一。在分析煤柱强度、煤柱载荷和从属面积法煤柱稳定性评价的基础上,定义了煤柱有效宽度为煤柱横截面内最大内切圆直径,引入采动载荷转移距离LTD,建立了基于载荷转移距离和煤柱有效宽度的煤柱稳定性评价方法。通过对规则煤柱和不规则煤柱稳定性的对比分析,表明新方法能有效改进传统从属面积法评价煤柱稳定性的局限性。为验证基于载荷转移距离和有效宽度的煤柱稳定性评价方法的可靠性,采用3DEC数值方法进行了模拟分析,模拟计算的煤柱载荷分布规律与理论计算一致,相对误差多在10%以下,最大相对误差为12.68%,验证了基于载荷转移距离的煤柱载荷计算的合理性。表明新方法不仅适用于规则煤柱,也适用于不规则煤柱,具有较好的普适性。
煤柱;有效宽度;载荷转移距离;稳定性评价;从属面积法
煤炭生产中不可避免地留设大量的保安煤柱、边角煤柱、隔离煤柱等,煤岩柱是煤矿地下结构的重要组成部分,起着支撑上覆岩体、维护巷道、保证安全和隔离危险的作用。对于建(构)筑物下、铁路下和水体下压煤开采,往往采用部分开采法,根据煤柱强度和煤柱载荷,留设一定尺寸的煤柱支撑上覆岩土体,达到既减小地表沉陷和采动损害又尽可能多的回收地下煤炭资源的目的。
尽管影响煤柱稳定性因素很多,包括煤柱强度、煤柱承受的载荷、矿井环境、时间过程以及煤柱与顶底板的相互作用等,但目前研究较多的是基于煤柱强度和煤柱载荷关系的稳定性评价方法[1-4]。传统的从属面积法计算煤柱载荷只考虑煤柱及其四周宽度相当于煤房一半区域之上的岩土体质量[1],是一种纯静态计算法[2],且无法顾及采动岩体的载荷转移过程;同时对于不规则煤柱,如何确定其宽度也同样制约着煤柱强度计算的可靠性。本文通过定义煤柱的有效宽度,引入载荷转移距离,尝试对规则煤柱和不规则煤柱稳定性进行较为客观的评价。
1 煤柱稳定性评价的从属面积法
1.1 煤柱强度公式
自1960年南非Coalbrook煤矿房柱式开采煤柱失稳破坏诱发矿井塌陷灾害以来,国外学者对煤柱强度开展了大量理论与试验研究。研究表明煤柱强度受煤柱尺寸、形状、不连续面、微结构和外部环境等影响;随着煤柱尺寸的增加,煤柱强度按指数规律减小,直到达到煤柱强度的下限;且按煤柱最小边长平方根除以煤柱高度的规律而变化[1],其一般表达式为Sp=Kwa/hb,其中,Sp为煤柱强度,MPa;K为井下煤柱中有代表性的立方体煤柱强度,MPa;w和h分别为煤柱的宽度和高度,m;a和b为常数。
基于南非和澳大利亚的实测结果,得到了多个煤柱强度估算公式[2]。
上述煤柱强度公式主要考虑了煤柱的宽度和高度,且随煤柱宽高比的增加而增大,如图1所示。
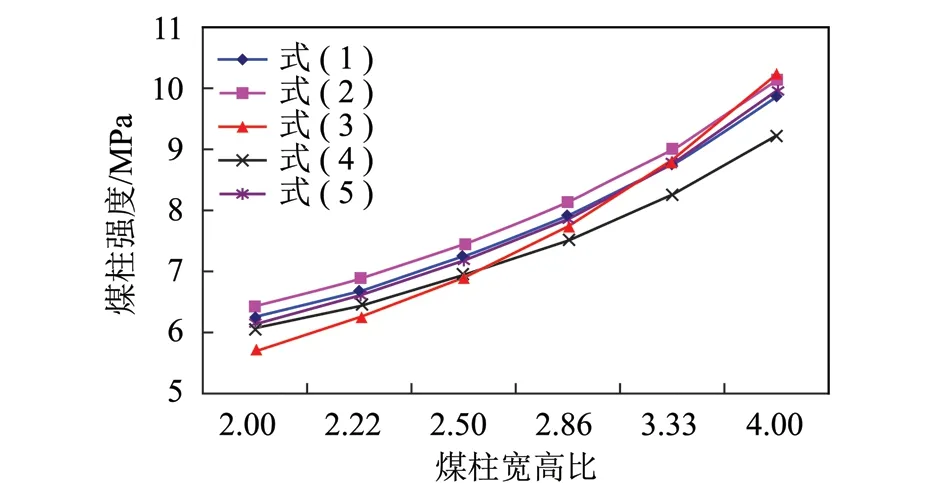
图1 煤柱强度与煤柱宽高比关系Fig.1 Pillar strength related to width height ratio
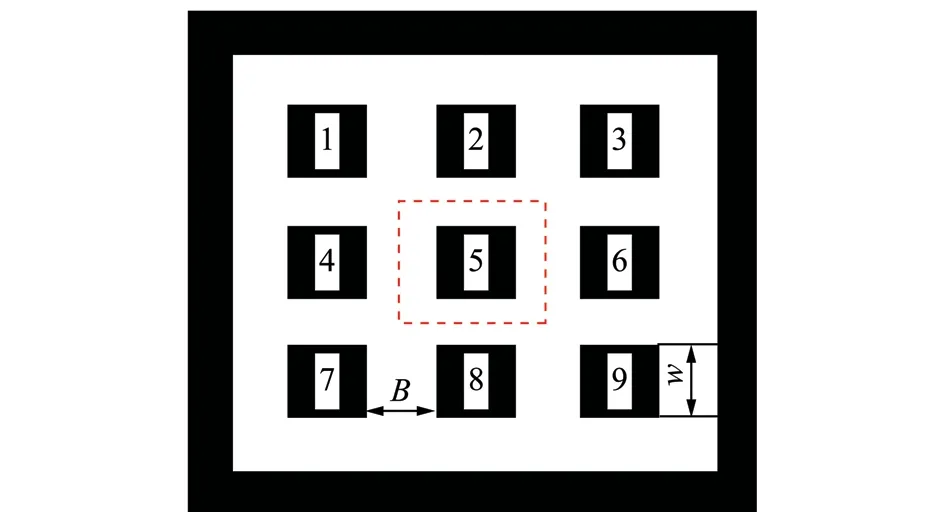
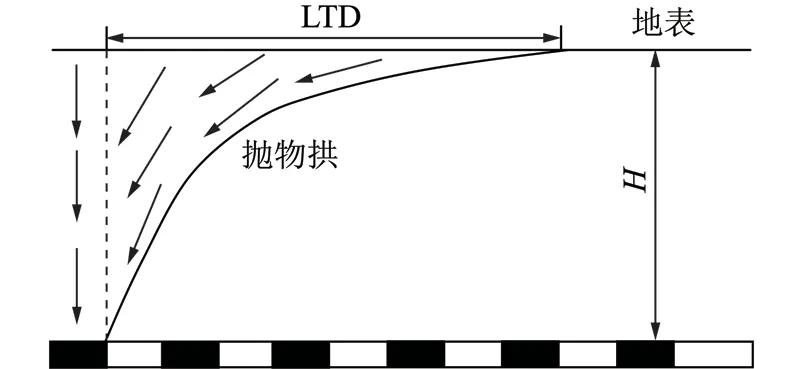
图1中5个煤柱强度公式计算结果差别不明显,其中煤柱宽度w=20 m。有研究者认为,式(1)~(5)只适用于2 Murali采用应变软化模型,通过FLAC3D数值模拟,也建立了如下所示的煤柱强度公式[3]为 其中,σc为煤的抗压强度,MPa;H为开采深度,m。认为煤柱强度不仅与煤柱宽高比有关,还与煤柱高度、开采深度有关。 从属面积法是煤柱载荷估算最常用的静态方法,该方法是基于开采后的从属面积之上的所有载荷都由煤柱承担的假设[4]。若开采深度为H,上覆岩层的平均密度为ρ,重力加速度为g,则原岩垂直应力可表示为σv=ρgH;对于图2所示的房柱式开采,房宽为B,柱宽为w,则煤柱所承受的载荷为 由式(7)可见,图2中的9个煤柱承受了相同的上部载荷。 图2 房柱式开采的煤柱载荷从属面积Fig.2 Tributary area for room-pillar mining 煤柱稳定性评价的安全系数定义为煤柱强度与煤柱所承受载荷之比,可表示为 SALAMON等对南非稳定矿柱和破坏矿柱统计分析后,发现稳定矿柱的安全系数集中在1.31.9之间,并建议安全系数的合理值为1.6[5]。KUSHWAHA研究认为,当安全系数FOS≥2时煤柱能保持长期稳定;当FOS=1~2时,煤柱能保持短期稳定,几年内会发生破坏;当FOS≥0.6时,煤柱只能保持数天内的稳定[6]。 对于规则煤柱,其有效宽度容易确定;而对于不规则煤柱,如何合理、客观地确定煤柱有效宽度将直接影响煤柱强度。1980年WAGNER借助于水力学中的水力半径概念,基于过水断面与湿周比值提出了煤柱的有效宽度并表示[7]为 图3 不同形状煤柱的有效宽度Fig.3 Effective width for different shape pillars 为避免Wagner煤柱有效宽度定义的局限性,考虑到煤柱的实际承受载荷情况,不规则煤柱的尖角处承受载荷能力很弱,煤柱的破坏往往从尖角处开始,由此提出不规则煤柱的有效宽度为煤柱的最大内切圆直径;该定义适用于所有规则和不规则煤柱情况,且在其它条件不变的情况下,煤柱强度随煤柱最大内切圆直径的增加而增强[8-9],如图3所示。煤柱最大内切圆直径作为煤柱的有效宽度,为各类煤柱稳定性评价奠定了基础。 对于图2所示的房柱式开采,根据传统的从属面积法,如果采出率和煤柱尺寸保持不变,则各煤柱强度和煤柱载荷也不变,从而导致各煤柱具有相同的安全系数。实际上,盘区内开采后各煤柱之间及开采区与未采区之间存在载荷的相互作用,其剖面示意图如图4所示。 图4 载荷转移距离LTD示意[10]Fig.4 Sketch map of load transfer distance[10] Abel根据50个煤矿、3个铀矿、1个碳酸钾矿和1个天然碱矿共55个矿井的实测载荷转移距离结果,以英尺为单位回归给出了采动后对矿柱影响的最大载荷转移距离公式[10];POULSEN按国际单位制对英制单位结果进行了转换,见式(10)和图5[2],回归的相关系数为0.871。表明在LTD范围内的开采活动,都会对该煤柱产生载荷转移影响。 其中,LTD为载荷转移最大距离,m;H为开采深度,m。开采深度越大,采动载荷转移距离越远。 图5 实测载荷转移距离与开采深度关系[2]Fig.5 Relationship between load transfer distance and mining depth[2] 根据载荷转移距离LTD,可进一步定义计算煤柱载荷的影响范围ZI,见式(11)。 其中,we为煤柱的有效宽度。式(11)表明,在ZI范围内的开采,都会对该中心煤柱载荷产生影响,其影响范围为以中心煤柱为圆心、以LTD+we/2为半径的圆,如图6所示。 图6 煤柱载荷计算范围Fig.6 Zone of influence for load calculation 假定房柱式开采的矿房宽度B=10 m,正方形矿柱宽度为we=10 m,煤柱高度为h=3 m,开采深度为H=150 m,上覆岩层平均密度为ρ=2 500 kg/m3,重力加速度g=10 m/s2,则采动载荷转移的最大距离LTD=38.265 m,计算煤柱载荷影响范围半径为LTD+we/2=43.265 m,原岩垂直应力σv=3.75 MPa。采用式(1)可计算得出煤柱强度Sp=10.06 MPa。 计算可得其安全系数为FOS=1.61。同理,可分别计算出2~9号煤柱的载荷和安全系数,见表1。从表中可见1号、3号、7号和9号煤柱安全系数最大且都等于1.61,2号、4号、6号和8号煤柱安全系数居中且都等于1.33,5号煤柱的安全系数为0.93,最小且不稳定;说明相同尺寸煤柱的安全系数随其所处采区的位置不同而变化。如果按照传统的从属面积法计算安全系数,则9个煤柱的安全系数均为0.67,显然低估了安全系数,与实际明显不符。 图7 规则煤柱的载荷计算Fig.7 Load calculations of regular pillars 其它条件保持不变,在图7原有的规则房柱式开采基础上回收一半煤柱,如图8所示,计算所得的煤柱稳定性评价结果见表2。 表2含有不规则煤柱的稳定性评价 煤柱编号载荷影响面积/m2采出面积/m2煤柱有效宽度/m煤柱宽高比煤柱强度/MPa煤柱载荷/MPa安全系数15880.6222520.338103.3310.066.561.5325880.6223283.010103.3310.068.491.1835880.6222619.6425.861.957.866.761.1645880.6223283.010103.3310.068.491.1855880.6224262.4815.861.957.8613.630.5865880.6222619.6425.861.957.866.761.16 图8 含有不规则煤柱的载荷计算Fig.8 Load calculations including irregular pillars 从表2中可见,随着盘区一半煤柱的回收,规则煤柱的安全系数随之降低;不规则煤柱随着有效宽度的减小,煤柱强度也减小;5号煤柱安全系数为0.58,属极不稳定煤柱;2号、3号、4号和6号煤柱处于短期稳定状态,表明采用煤柱有效宽度和载荷转移最大距离LTD可以较客观地评价规则和不规则煤柱的稳定性。 数值模拟方法被国内外学者广泛应用于煤柱应力分布、煤柱强度和煤柱破坏分析[11-17]。为了检验基于载荷转移距离的煤柱稳定性评价理论方法的可靠性和有效性,本文采用3DEC(三维离散单元法)软件进行了煤柱载荷的数值模拟验证。数值模拟时,煤柱、煤房尺寸以及开采深度都与前述理论分析相同。矿房宽度B=10 m ,正方形矿柱宽度we=10 m ,煤柱高度h=3 m,开采深度H=150 m。上覆岩层平均密度ρ=2 500 kg/m3,重力加速度g=10 m/s2。至于上覆岩层的组成,按一般情况考虑,建模时将数值模型共分为7层,第6层为煤层,第7层为底板岩层,底板主要由泥岩构成,上覆岩层则为5层,每层高度30 m,最上层(第1层)为松散层,往下依次分别为泥岩、泥砂岩互层、中粒砂岩和细粒砂岩,岩层参数参考相关资料获取,所建数值模型如图9所示。覆岩的物理力学参数以王庄煤矿6206工作面为背景参考取值,模型的x和y方向的长度均为250 m,z方向的高度为180 m。 首先模拟单一煤柱开采后的载荷转移距离,即采出中心煤柱周围上下左右宽度各为10 m(矿房宽度)范围的煤层,如图10所示的绿色区域,当图中的绿色区域采出后,然后查看开采后竖向应力的传播范围,如图11中的虚线圆(红色)所表示的范围。通过计算处理,数值模拟的最大载荷转移距离为36.099 m,与理论计算所得的载荷转移距离38.265 m接近,相差2.166 m,证明了利用式(11)计算煤柱载荷的影响范围是较为可靠的。 图9 数值模拟计算模型Fig.9 Numerical simulation model 图10 载荷转移距离模拟计算数值模型Fig.10 Numerical model for calculation load transfer distance 图11 单一煤柱载荷最大转移距离模拟Fig.11 Simulation results of load transfer distance for single coal pillar 图12 规则煤柱竖向应力分布Fig.12 Distribution of vertical stress for regular coal pillars 为了验证规则煤柱载荷计算评价结果的可靠性,进一步开挖形成如图12所示的模拟结果,统计计算9个规则煤柱的数值模拟载荷情况见表3;数值模拟9个煤柱的载荷分布规律与理论计算结果一致,最大相对误差为12.68%。进一步回收煤柱的模拟结果如图13所示,统计计算的3个规则煤柱和3个不规则煤柱的数值模拟载荷情况见表4;数值模拟6个煤柱的载荷分布规律也与理论计算结果一致,最大相对误差为11.22%。 图13 规则与不规则煤柱竖向应力分布Fig.13 Distribution of vertical stress for regular and irregular coal pillars 煤柱编号煤柱中心点坐标/mXYZ理论计算载荷/MPa模拟计算载荷/MPa相对误差/%1105145306.236.798.912125145307.557.803.313145145306.236.798.914105125307.557.803.3151251253010.89.94-7.886145125307.557.924.907105105306.237.0212.688125105307.557.803.319145105306.236.9611.72 表4规则与不规则煤柱模拟计算载荷值与理论计算载荷对比 煤柱编号煤柱中心点坐标/mXYZ理论计算载荷/MPa模拟计算载荷/MPa相对误差/%1105145306.567.3011.222125145308.498.763.183143147306.767.328.214105125308.498.581.0651231273013.612.5-8.586103107306.767.379.02 3DEC数值模拟结果表明,不论规则煤柱还是不规则煤柱的模拟计算载荷分布规律与理论计算的分布规律都一致,数值模拟煤柱载荷的相对误差多在10%以下,最大相对误差为12.68%,从而验证了基于载荷转移距离的煤柱载荷计算的可靠性。 (1)通过定义最大内切圆直径作为煤柱的有效宽度,可以较客观地评价规则煤柱和不规则煤柱强度。 (2)通过引入载荷转移距离,改进了传统从属面积法计算煤柱载荷的局限性,使得计算的煤柱安全系数与实际更接近。 (3)煤柱载荷计算的从属面积法和改进的从属面积法都属于静态方法,目前还无法有效考虑开采的动态时间过程;同时煤柱强度受矿井环境的风化、侵蚀影响,在长期载荷作用下会产生流变和强度降低现象。由于煤柱稳定性影响因素多,力学过程复杂,未来还需进一步的系统研究、实验和探索。 [1] PENG S S.煤矿地层控制[M].高博彦,韩持,译.北京:煤炭工业出版社,1984. [2] POULSEN B A.Coal pillar load calculation by pressure arch theory and near field extraction ratio[J].International Journal of Rock Mechanics & Mining Sciences,2010,47(7):1158-1165. [3] MURALI G,SHEOREY P R,KUSHWAHA A.Numerical estimation of pillar strength in coal mines[J].International Journal of Rock Mechanics and Mining Sciences,2001,38(8):1185-1192. [4] HAUQUIN T,DECK O,GUNZBURGER Y.Average vertical stress on irregular elastic pillars estimated by a function of the relative extraction ratio[J].International Journal of Rock Mechanics & Mining Sciences,2016,83:122-134. [5] 邹友峰,胡友健,郭增长.采动损害与防护[M].徐州:中国矿业大学出版社,1996. [6] KUSHWAHA A,BANERJEE G.Exploitation of developed coal mine pillars by shortwall mining[J].International Journal of Rock Mechanics & Mining Sciences,2005,42(1):127-136. [7] WAGNER H.Pillar design in coal mines[J].Journal of the South African Institute of Mining and Metallurgy,1980,1:37-45. [8] 彭小沾,崔希民,王家臣,等.基于Voronoi图的不规则煤柱稳定性分析[J].煤炭学报,2008,33(9):966-970. PENG Xiaozhan,CUI Ximin,WANG Jiachen,et al.Stability analysis of irregular coal pillars based on Voronoi diagram[J].Journal of China Coal Society,2008,33(9):966-970. [9] CUI Ximin,GAO Yongge,YUAN Debao.Sudden surface collapse disasters caused by shallow partial mining in Datong coalfield,China[J].Natural Hazards,2014,74(2):911-929. [10] ABEL J F.Soft rock pillars[J].International Journal of Mining and Geological Engineering,1988,6(3):215-248. [11] 王永秀,齐庆新,陈兵,等.煤柱应力分布规律的数值模拟分析[J].煤炭科学技术,2004,32(10):59-62. WANG Yongxiu,QI Qingxin,CHEN Bing,et al.Analysis on digital simulation for stress distribution law of coal pillar[J].Coal Science and Technology,2004,32(10):59-62. [12] 郑百生,谢文兵,窦林名,等.不规则煤柱作用下工作面开采的三维数值模拟[J].煤炭学报,2006,31(2):137-140. ZHENG Baisheng,XIE Wenbing,DOU Linming,et al.3D simulation on caving of face affected by irregular pillar[J].Journal of China Coal Society,2006,31(2):137-140. [13] 尹尚先.陷落柱防水煤柱留设对围岩变形影响的数值模拟[J].煤炭学报,2006,31(2):179-182. YIN Shangxian.Numerical simulation of influence of water barrier pillars for subsided column on rock failure in mining process[J].Journal of China Coal Society,2006,31(2):179-182. [14] WANG Shuili,HAO Shengpeng,CHEN Yong,et al.Numerical investigation of coal pillar failure under simultaneous static and dynamic loading[J].International Journal of Rock Mechanics & Mining Sciences,2016,84:59-68. [15] JAISWAL A,SHRIVASTVA B K.Numerical simulation of coal pillar strength[J].International Journal of Rock Mechanics & Mining Sciences,2009,46:779-788. [16] SINGH R,SINGH S K,KUSHWAHA A,et al.Stability of the parting between coal pillar workings in level contiguous seams during depillaring[J].International Journal of Rock Mechanics & Mining Sciences,2012,55:1-14. [17] JAISWAL A,SHRIVASTVA B K.Stability analysis of the proposed hybrid method of partial extraction for underground coal mining[J].International Journal of Rock Mechanics & Mining Sciences,2012,52:103-111. Pillarstabilityevaluationbasedonloadtransferdistanceandpillareffectivewidth CUI Ximin1,LU Ying1,ZHANG Bing2 (1.CollegeofGeoscienceandSurveyingEngineering,ChinaUniversityofMiningandTechnology(Beijing),Beijing100083,China; 2.SchoolofResourcesandEnvironmentalScience,ShijiazhuangUniversity,Shijiazhuang050035,China) Pillar stability evaluation is a major content and premise for room and pillar mining design.On the basis of analysis of pillar strength,pillar load and stability evaluation with tributary area method,the effective width is defined as the maximum diameter of inscribed circle in the coal pillar and is used to calculate the pillar strength.By leading into the load transfer distance (LTD),the pillar stability evaluation method is established based on the LTD and efficient width.Compared with the results of stability evaluation for regular and irregular pillars,the new method can effectively improve the limitation of traditional stability evaluation for tributary area method.In order to verify the reliability of new pillar stability evaluation method based on the load transfer distance and the effective width,the 3DEC numerical simulation is applied and analyzed.The distribution of numerical simulated pillar loads are consistent with theoretical calculations,almost all the relative errors are below 10% and the maximum relative error is 12.68%.That is to say that the new evaluation method has a good universality not only suitable for regular pillars but also for irregular pillars. coal pillar;effective width;load transfer distance;stability evaluation;tributary area method 崔希民,逯颖,张兵.基于载荷转移距离和有效宽度的煤柱稳定性评价方法[J].煤炭学报,2017,42(11):2792-2798. 10.13225/j.cnki.jccs.2017.0059 CUI Ximin,LU Ying,ZHANG Bing.Pillar stability evaluation based on load transfer distance and pillar effective width[J].Journal of China Coal Society,2017,42(11):2792-2798.doi:10.13225/j.cnki.jccs.2017.0059 TD823.5 A 0253-9993(2017)11-2792-07 2017-01-11 2017-09-18责任编辑常 琛 国家自然科学基金资助项目(51474217,41071328) 崔希民(1967—),男,辽宁宽甸人,教授,博士。Tel:010-62339305,E-mail:cxm@cumtb.edu.cn1.2 煤柱载荷计算的从属面积法
1.3 煤柱稳定性评价的安全系数
2 煤柱有效宽度与载荷转移距离
2.1 煤柱有效宽度
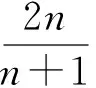

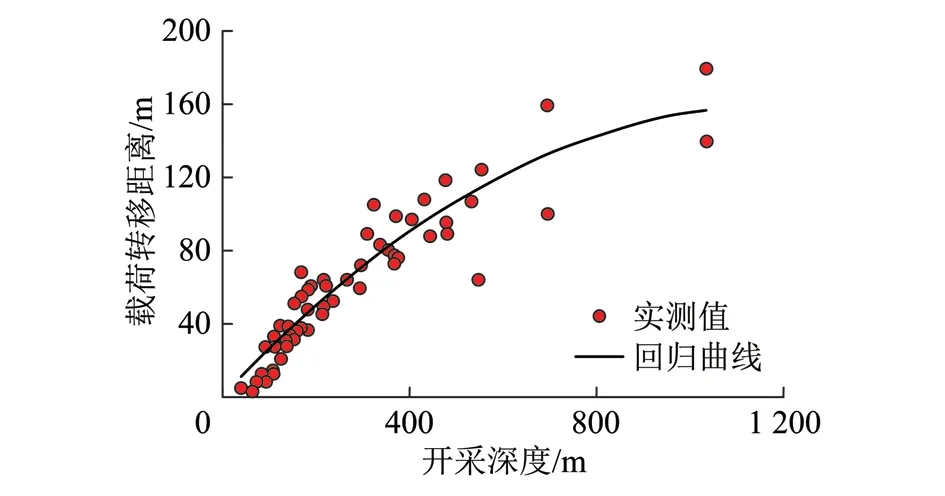
2.2 采动影响下的载荷转移距离


3 基于载荷转移距离的煤柱稳定性评价方法
3.1 规则煤柱的稳定性评价


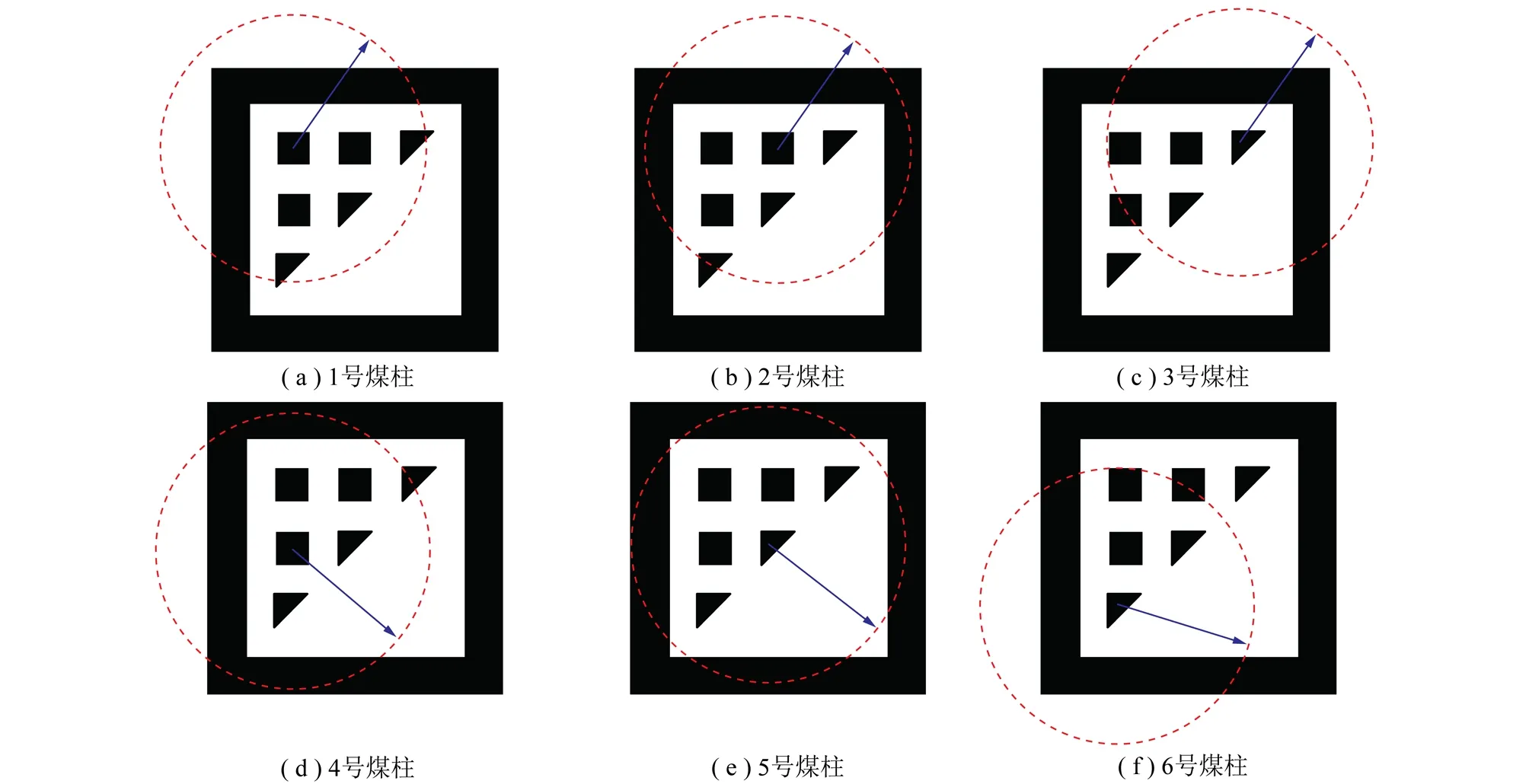
3.2 含有不规则煤柱的稳定性评价
Table2Stabilityevaluationsincludingirregularpillars
4 数值模拟验证分析
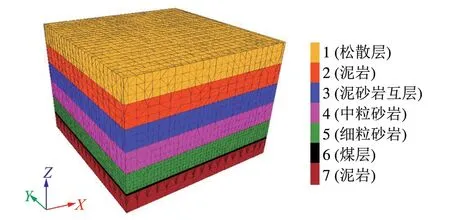




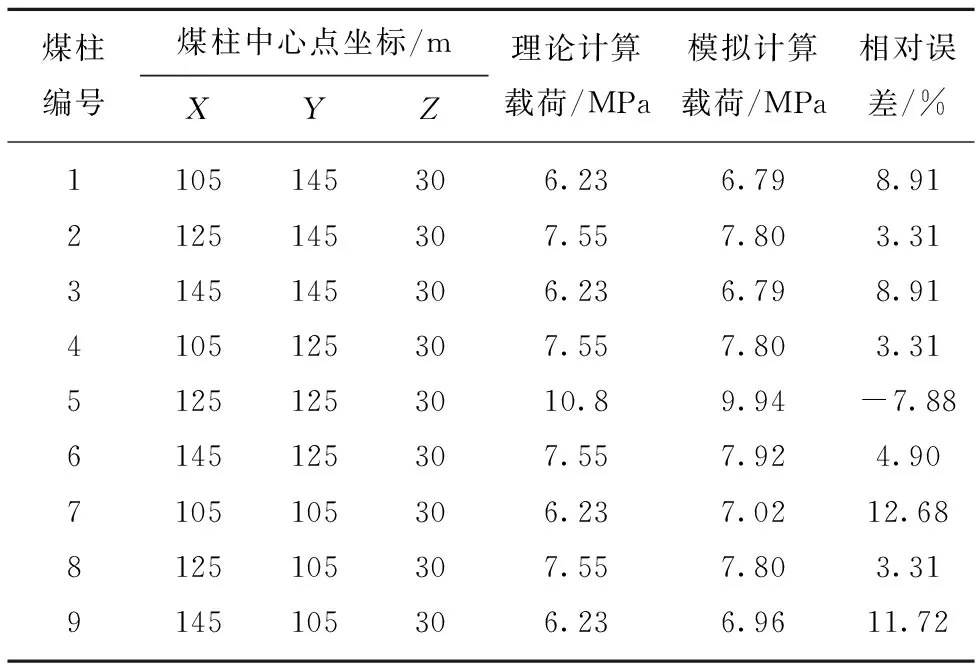
Table4Comparisonsofcalculatedloadandtheoreticalloadforregularandirregularcoalpillars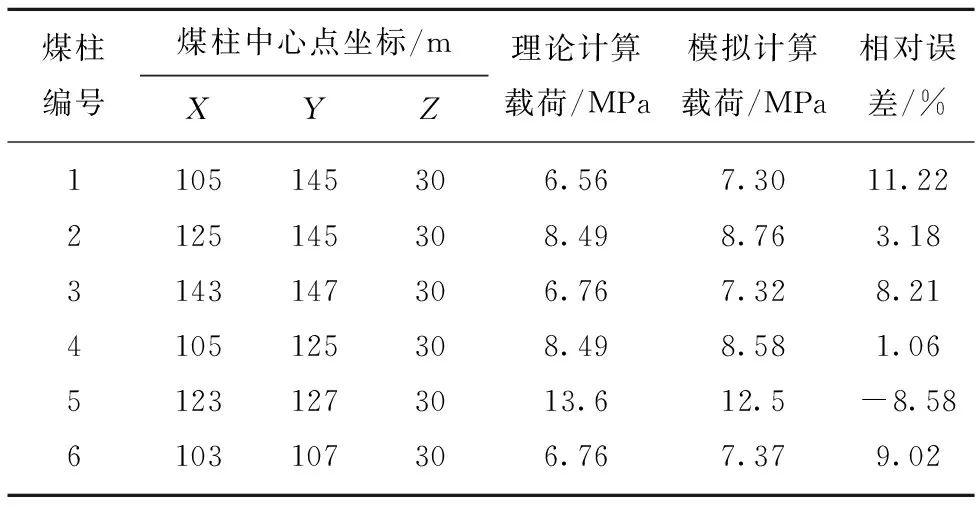
5 结 论

