模糊自整定PID在脱硝控制系统中的应用

金秀章，张少康

(华北电力大学控制与计算机工程学院，河北 保定 071003)

模糊自整定PID在脱硝控制系统中的应用

金秀章，张少康

(华北电力大学控制与计算机工程学院，河北 保定 071003)

针对火电厂脱硝控制系统的大迟延、非线性、时变等特点，提出了一种模糊自整定PID控制策略。对脱硝控制系统中选择性催化还原(SCR)烟气脱硝原理和传统的出口NOx控制策略进行了研究。根据系统的性能指标，确定了PID参数的模糊规则整定表。分析了初始论域对系统控制性能的影响，根据遗传算法得到初始的PID参数，利用模糊推理原则修改PID参数，以满足被控对象变化时的需求。通过Matlab对不同负荷下的被控对象进行了仿真。其结果表明：与传统PID控制策略相比，模糊自整定PID控制策略在快速性、准确性、鲁棒性方面有了明显的提升。该控制策略可有效应用于脱硝控制系统。

脱硝控制系统； 选择性催化还原； 模糊自整定； 遗传算法； Matlab； PID

0 引言

近年来，中国的大部分地区都有不同程度的雾霾，华北地区尤为严重。导致雾霾的主要原因是火电厂烟气排放不达标。国际上，特别是欧洲和美国，目前应用较广泛的脱硝技术是选择性催化还原(selective catalytic reduction，SCR)法。随着国内环境的变化，人们逐渐开始将脱硝技术应用于电厂[1]。

目前，脱硝系统中主要采用传统的PID控制[2]。对于精确的数学模型，PID有很好的控制效果。而脱硝系统具有大迟延、非线性、时变的特点，当被控对象变化时，传统的PID控制无法满足控制要求[3]。

针对上述问题，提出了一种模糊自整定PID控制方法。该方法可以根据被控对象的变化在线调节PID中的参数，以确保被控对象发生变化时能达到期望的结果[4]。仿真表明，在被控对象变化时，基于模糊自整定PID控制方法的响应速度和调节时间较传统PID控制方法有明显改善。

1 脱硝控制系统

1.1 SCR烟气脱硝原理

SCR技术能够把烟气中的NOx通过催化剂转换成对人体没有危害的N2和H2O。一般而言，电厂中的催化剂选用以TiO2为载体的V2O2或MoO2，温度设置为催化剂所需的温度，温度范围通常为300～420 ℃。反应器放在省煤器和空预器之间，选用液氨为还原剂。液氨蒸发以后，与通过稀释风机后的空气混合，而后经分配格栅送到反应器中与NOx进行混合[5]。

4NH3+4NO+O2→ 4N2+6H2O

(1)

4NH3+2NO2+O2→ 3N2+6H2O

(2)

NOx的脱除效率与催化剂的性能、反应器内的温度、烟气内的含氧量、喷氨量等诸多因素有关。SCR脱硝原理如图1所示。

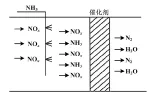
图1 SCR脱硝原理图

1.2 传统喷氨量和出口NOx浓度控制

脱硝控制系统应用较多的方法是串级PID控制。该控制又分为主、副2个回路。主回路控制出口NOx浓度。副回路控制喷氨量，当出现扰动时，可以快速减小扰动。将测得的SCR反应器入口和出口的NOx设定值的差值与烟气流量相乘，得到实际脱除的NOx值；再利用NH3和NOx的物质的量之比求得理论喷氨值。将该值作为前馈信号，与外回路控制器的输出相加，得到内回路的设定值[6]。脱硝控制系统结构如图2所示。

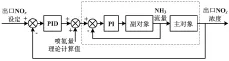
图2 脱硝控制系统结构图

在实际运行过程中，被控对象的数学模型并非一直稳定的。当负荷升高时，首先加大的是送风量。这段时间内，因为风过量导致燃烧产生的NOx增加，而喷氨量还没有变化，所以被控对象的静态增益系数和积分时间常数都会改变。当数学模型的参数变动时，选用单一的PID控制不能达到系统的需求。基于此，选取模糊自整定PID控制替代原有的PID控制，即使被控对象变化也可满足要求。

由于最终控制的是出口NOx浓度，所以需先使用PI调节副回路中的副对象，然后将其与主对象结合，再通过模糊自整定PID进行控制。当负荷在350 MW、450 MW、550 MW下，主对象、副对象及整合后的传递函数如表1所示。

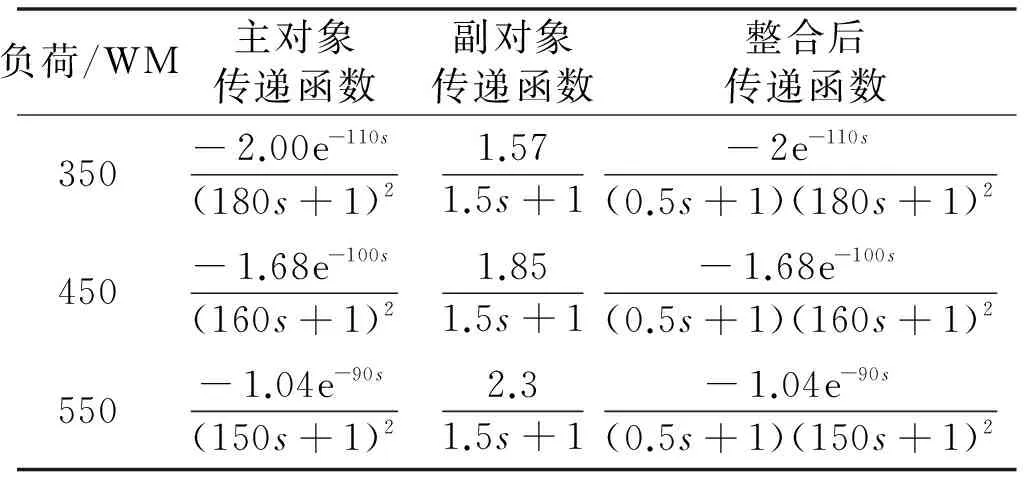
表1 传递函数表

2 模糊自整定PID控制器

PID控制要求模型结构精确。在实际应用中，大多数的工业过程是非线性、时变的。模糊控制无需被控对象的动态特性，仅根据输出误差即可修改参数，并且鲁棒性较好，因此可以应用于脱硝控制系统中。

模糊自整定PID控制结构如图3所示。图3中：D为扰动。以误差(e)和误差的变化率(ec)作为控制器的输入，根据模糊推理原则，得到e、ec和Kp、Ki、Kd的关系。当误差改变时，可以在线修改3个参数，使被控对象的性能得到较大的提升[7]。

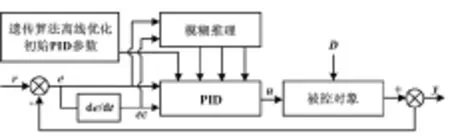
图3 模糊自整定PID控制结构图

2.1 模糊规则整定表原则

首先找到e、ec和Kp、Ki、Kd的关系，并根据系统的稳定性、调节时间、超调量等指标，得到以下整定原则。

①|e|很大。

此时，应该加大比例系数，使系统响应加快，从而快速减小误差。为了防止微分过饱和现象，应该取较小的Kd。由于积分饱和会令系统的超调量变大，所以Ki取值应该尽可能地小。

②|e|为中间大小。

此时，因为误差还是比较大的，所以比例系数Kp和微分系数Kd取较大值。Ki选相对小的数，可以保证系统具有一定的超调量。

③|e|比较小。

此时，应合理增大Kp、Ki的值，以尽快消除系统的静态误差。微分环节反映的是误差变化率的信息，具有超前调节作用。所以，随着误差变化率的增大，Kd也应该随之增大[8]。

2.2 模糊自整定PID参数选取

选取e和ec作为输入，Kp、Ki、Kd作为输出。由模糊规则整定原则确定Kp、Ki、Kd的规则，如表2所示。最终，可以得到PID的3个参数的调整量[11]。

表2 模糊规则表

当输入的论域很大时，扰动量小而使控制器的输出只是停留在初始的PID参数，模糊推理改变不了PID参数。在选取输入论域时，要根据实际过程来确定。本文最终确定输入初始论域为(-7，7)。系统的输出论域范围对系统的影响很大。输出的论域就是执行器一次变化的最大范围，当选择的初始论域较大时，控制系统的响应速度会较快，超调也会比较大；当选择的初始论域较小时，系统的响应速度会较慢，但是超调比较小。由于输出初始论域的选取在实际中受到执行器本身的限制，所以要结合实际工况来确定输出的初始论域[9]。

选取e、ec、Kp、Ki、Kd的等级量论域为：[-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6]；模糊子集为[NBNMNSZOPSPMPB]，其含义依次为负大、负中、负小、零、正小、正中、正大[10]。隶属度函数一般分为三角形、钟形、梯形等几类。隶属度函数形状为三角形曲线的精度较高，相对钟形曲线来说可以更简单地表示出变量的隶属度。根据三角形隶属度函数，可以得到e、ec的等级量和模糊量之间的关系。

根据表1中负荷为350 MW的情况，分析初始的输出论域对系统的影响[12]。传递函数为：

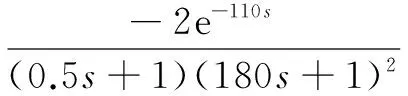
(3)

因为整定的是PID的3个参数，一般主要起作用的是Kp和Ki，所以对Kd取较小的值。设Kd论域为(1，7)，分析Kp、Ki在不同情况下对系统的影响。

首先，分析Kp初始论域的影响。设Ki论域为(-0.004，-0.003 8)，当Kp初始论域分别为(-3，-2.9)、(-3，-2.6)、(-3，-2)、(-3，-1.5)时，仿真结果如图4所示。

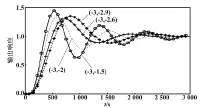
图4 Kp初始论域不同时的控制效果

其次，分析Ki初始论域的影响。选取Kp初始论域为(-3，-0.26)，当Ki的初始论域分别为(-0.004，-0.003 8)、(-0.004，-0.003)、(-0.004，-0.002)、(-0.004，-0.001)时，仿真结果如图5所示。

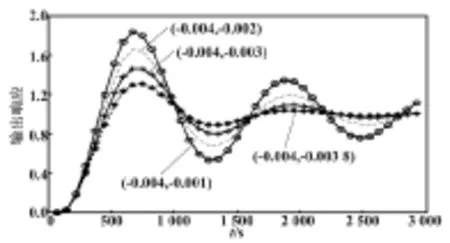
图5 Ki初始论域不同时的控制效果

从图4可以看出，Kp初始论域的不同主要是对系统的响应速度有影响。选取的初始论域越大，Kp的变化量ΔKp也越大。图4中，初始论域为(-3，-1.5)时的响应最快，但是超调量也比较大，并且震荡频繁；随着论域的减小，响应速度变慢，超调减小。综合考虑，选取Kp论域为(-3，-2.6)。

Ki论域的不同对超调量有很大影响。从图5可以看出，随着论域的增大，超调增大，震荡频繁，系统的控制效果也会逐渐变差，综合考虑选取Ki论域为(-0.004，-0.003 8)。

3 遗传算法优化

在进行在线修正PID参数时，应该设定1个初始PID参数。1个好的初始参数可以在被控对象的数学模型发生变化时，尽快地达到稳态值。以负荷350 MW为例进行分析，在不同的初始PID参数下，计算响应曲线与期望值的误差。取误差的绝对值，得到如图6所示的误差绝对值曲线。

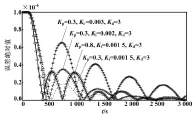
图6 误差绝对值曲线

由图6可知，根据选取初始PID参数的不同，系统的响应也不同。当Ki、Kd不变时，随着Kp绝对值的增大，系统的响应速度变快，但是超调也增大。当Kp、Kd不变时，由于Ki绝对值的增大，系统超调也随之增大，并且震荡频繁。所以，准确地判断初始PID参数，可以较好地提升被控对象的控制性能。这里用遗传算法优化初始PID参数。

①参数编码。

常见的参数编码方法有：二进制编码、格雷码编码、浮点数编码等。二进制编码具有操作简单，执行方便，有利于实现交叉等遗传操作，符合最小字符集原理，便于模式定理分析等优点[13]。因此，本文选用二进制编码。

②适应度函数的选取。

遗传算法根据适应度函数来更新种群，然后得到每个个体的适应度，并选取最优的结果。这里选用的适应度函数为时间乘绝对误差积分(integral time absolute error，ITAE)准则的倒数[14]，即：

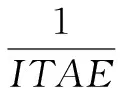
(4)

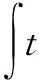
|e(i×DT)×DT|

(5)

式中：DT为仿真计算的步距；LP为仿真计算的步数。

由该方法得到的阶跃响应曲线具有超调小和响应速度快的特点，但是控制器输出会出现剧烈震荡。基于以上研究，加入控制器输出作为新的准则，如式(6)所示。

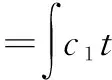
c2×u(i×DT)×u(i×DT)]×DT

(6)

式中：c1和c2为误差和控制器输出的权系数，一般选取c1=0.02、c2=0.98。

在遗传的开始阶段，可能出现1个或多个异常个体。异常个体可能因为太突出而导致遗传进化失败。此外，多次遗传进化以后，种群适应度均值和个体的最佳适应度相差不大。此时，个体之间的竞争就会减弱，遗传操作就会变得缓慢。对此，应该扩大个体之间的差异，从而快速地找到最优值[15]。选用线性尺度变换，线性修改后如式(7)所示：

f′=af+b

(7)

式中：f′为修改后的适应度函数；f为开始时的适应度函数。

a、b应该具有以下特性：修改的适应度函数平均值和开始的适应度函数的平均值相等，以保证群体中的个体遗传到下一代；修改的适应度函数最大值应该是开始的适应度函数最大值的C倍，以保证最好的个体可以复制C倍到下一代[16]。

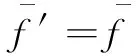
(8)

(9)

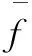
试验表明，当种群规模n为50～100时，C选取1.2～2，最终得到a、b的值。

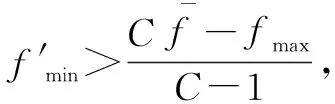
(10)

否则，用式(11)计算a、b：

(11)

③遗传操作。

遗传操作分为选择、交叉和变异。

选择就是从群体中选择优质个体、淘汰劣质个体，应用方法主要有适应度比例法、最佳个体保留法等。本文选用适应度比例方法。其又被称为轮盘赌选择。设群体规模为n，第i个个体的适应度为fi，则被选中的概率为：

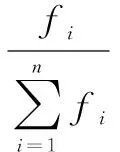
(12)

(13)

交叉是对2个上代的基因进行重组或互换，可以保留2个个体的优秀基因。对于二进制编码，就是根据设定的交叉概率来确定个体之间是否要进行交叉，然后设定交叉点，并通过交换个体的二进制编码串完成交叉运算[17]。本文选用的是单点交叉，选取的交叉概率Pc=0.6。交叉的具体实现方法为：

个体A:0 1 0| 0 1-0 1 1 0 1 新的个体A

个体B:0 0 1| 0 1-0 0 0 0 1 新的个体B

变异操作就是修正个体中的基因值，二进制编码就是对编码串取反。本文选用基本变异。具体方法为：在交叉完以后的个体编码中随机挑选1个或多个设定点，然后以变异概率Pm来决定这些点是否需要变异，这里选取Pm=0.002。变异的具体实现方法为：

个体A:1 0 1 0 1-1 1 1 0 0新的个体A

4 仿真结果与分析

利用遗传算法，分别优化3个负荷下的初始PID参数，并结合实际工况，得到最终的初始PID参数：Kp=-0.34，Ki=-0.001 5，Kd=5。当负荷增加时，被控对象的模型参数是单调变化的。在不同的负荷之间插入不同的数学模型，稳定后加入扰动D=0.8；然后，对插入的模型进行仿真。插入的数学模型如表3所示。

表3 数学模型

在Matlab环境下，采用模糊自整定PID控制和传统PID控制，分别对模型1、模型2和模型3进行仿真。仿真结果如图7所示。

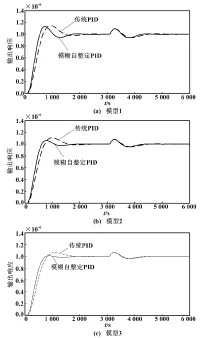
图7 仿真结果

由图7可知，与传统PID控制相比，模糊自整定PID控制的鲁棒性得到了加强，系统的响应速度有较明显的提升，加入扰动后的自调整能力也得到了改善。

5 结束语

根据不同负荷下传递函数易变的特点，利用模糊自整定PID算法修改参数来控制被控对象。初始的PID参数由遗传算法优化得到。在不同的情况下进行Matlab仿真，可知系统响应速度得到了较大的提高，抗干扰能力和鲁棒性也得到了增强。该方法为脱硝控制系统中出口NOx的浓度在线控制提供了一种有效的控制策略。

[1] 赵毅,朱洪涛,安晓玲,等.燃煤电厂SCR烟气脱硝技术的研究[J].电力环境保护,2009,25(1):7-10.

[2] 曹梦龙,刘川来,王乾.基于参考模型的自适应模糊控制系统设计与仿真[J].青岛科技大学学报(自然科学版),2005,26(1):82-84.

[3] 杨超.脱硝装置控制系统的整合和优化[D].杭州：浙江大学,2015:33-41.

[4] 葛金来,张承慧,崔纳新.模糊自整定PID控制在三自由度直升机实验系统中的应用[J].信息与控制,2010,39(3):342-347.

[5] 禾志强,祁利明.SCR烟气脱硝系统的运行方式及控制[J].热力发电，2009,38(11):93-96.

[6] 金秀章,尹子剑,张少康,等.加权多模型自适应控制在脱硝系统中的应用[J].自动化仪表,2016,37(9):82-85.

[7] 覃来丰,冯晓露.磨煤机模糊自整定PID控制器的设计和仿真[J].电站系统工程,2007,23(4):65-67.

[8] 何菊侃,王广军,苟小龙,等.模糊自整定PID及其在磨煤机控制中的应用[J].热力发电,2004,32(9):55-57.

[9] 武彬.模糊自整定PID控制器的设计与开发[D].保定：华北电力大学,2015:21-25.

[10]杨世勇,徐国林.模糊控制与PID控制的对比及其复合控制[J].自动化技术与应用,2011,30(11):21-25.

[11]李茜,李彬,朱雪丹.模糊自整定PID控制器的设计与仿真[J].化工自动化及仪表,2010,37(3):25-28.

[12]王安,杨青青,闫文宇.模糊自整定PID控制器的设计与仿真[J].计算机仿真,2012,29(12):224-228.

[13]杨梅.GA-BP算法优化及其在污水参数软测量中的应用研究[D].重庆:重庆大学,2008:34-35.

[14]刘道.基于改进粒子群优化算法的PID参数整定研究[D].衡阳:南华大学,2012:30-35.

[15]曾振平,陈增强,袁著祉.基于新的误差积分准则的PID控制器优化[J].控制工程,2004,11(1):52-54.

[16]赵振勇,王力,王保华,等.遗传算法改进策略的研究[J].计算机应用,2006,26(S2):189-191.

[17]俞书伟,张华雨,杨林.遗传算法在库存模糊逻辑控制中的应用[J].中国管理科学,2000,8(2):34-40.

ApplicationoftheFuzzySelf-TurningPIDintheDenitrationControlSystem

JIN Xiuzhang，ZHANG Shaokang

(School of Control and Computer Engineering,North China Electric Power University，Baoding 071003，China)

In accordance with the characteristics of NOxreduction control system in coal-fired power plant,e.g.,large time delay,non-linearity and time-varying,etc.,a control strategy based on fuzzy self-tuning PID is proposed.The principle of selected catalytic reduction(SCR) flue gas denitration and traditional outlet NOxcontrol strategy in NOxreduction control system are studied.Then,according to the performance indexes of system,the fuzzy rule tuning table of PID parameters is determined.The influence of the initial domain on control performance of system is analyzed,the initial PID parameters is obtained according to genetic algorithm,and the PID parameter are modified by the fuzzy inference principle,to meet the demand for varying controlled object.Simulation of controlled objects under various loads is conducted by using Matlab.The results show that comparing with the traditional strategy,the rapidity,accuracy and robustness have greatly improved by the fuzzy self-tuning PID control strategy.This control strategy can be effectively applied in the NOxreduction control system.

Denitration control system； Selected catalytic reduction(SCR)； Fuzzy self-tuning； Genetic algorithm； Matlab； PID

修改稿收到日期:2017-01-13

金秀章(1969—)，男，博士，副教授，主要从事大型发电机组先进控制策略的研究工作，E-mail：sysjinxz@163.com

TH86;TP273

A

10.16086/j.cnki.issn1000-0380.201712008