一类具有交叉扩散的捕食-食饵模型的共存性

王晶晶，贾云锋

(陕西师范大学数学与信息科学学院，陕西 西安 710062)

一类具有交叉扩散的捕食-食饵模型的共存性

王晶晶，贾云锋

(陕西师范大学数学与信息科学学院，陕西 西安 710062)

讨论了一类新型的具有交叉扩散项的捕食-食饵模型非常数正解的存在性。首先，给出了正解的先验估计；其次，利用度理论得到非常数正解的存在性。结果表明：对于给定的交叉扩散系数，当捕食者与食饵的增长率控制在一定范围内时，两物种可以共存。

捕食-食饵模型；交叉扩散；先验估计；度理论；共存性

在经典的反应扩散系统中，种群的扩散行为仅与种群自身的随机移动有关，即扩散行为仅依赖于种群的自我扩散。事实上，在实际的生态系统中，种群的扩散过程还依赖于种群间的相互渗透，也就是依赖于种群间的交叉扩散行为。带有交叉扩散项的捕食模型能更加准确地反映捕食者和食饵之间的相互关系[1-3]。近年来，带有交叉扩散项的捕食模型受到了人们的关注。例如，文献[4]研究了三种群的交叉扩散捕食模型，证明了交叉扩散能够导致系统产生空间斑图；文献[5-7]研究了带有交叉扩散项的捕食模型正常数解的稳定性；文献[8-11]研究了带有交叉扩散项的捕食模型非常数正解的不存在与存在性。

在一些带有Neumann边界条件的捕食模型中，如果只考虑含一个交叉扩散项的情形，那么模型在一定条件下不会产生非常数正解。例如，文献[9]中讨论了含一个交叉扩散项的捕食模型， 证明了在一定条件下模型没有非常数正解。但是，如果考虑两个交叉扩散项，那么情形就不同了，在同样的条件下模型可能产生非常数正解。同时，从生态学实际来看，当捕食者进行捕食时，食饵会向着远离捕食者的方向移动以免被捕食，这就需要再引入一个交叉扩散项来模拟更加符合实际现象的捕食-食饵关系。基于这些考虑，本文引入如下含两个交叉扩散项的捕食模型

(1)

其中Ω为Rn(n≥1)中具有光滑边界∂Ω的有界开区域，ν为边界∂Ω上的单位外法向量；u,v分别表示食饵和捕食者的种群密度；a,b分别为u,v的固有增长率；m1为v的捕食率，m2为v的转化率；边界条件表示u和v生活在同一个封闭的环境内；di>0(i=1,2)表示u和v的自我扩散系数；d1d3和d2d4为交叉扩散系数，其中d3,d4>0，

-d1Δ[(1+d3v)u]=-div{▽(d1u+d1d3uv)},

-d2Δ[(1+d4u)v]=-div{▽(d2v+d2d4uv)},

-▽(d1u+d1d3uv)=-d1d3u▽v-(d1+d1d3v)▽u,

-▽(d2v+d2d4uv)=-d2d4v▽u-(d2+d2d4u)▽v

当d3>0时，-d1d3u▽v反应了食饵逃离捕食者，即食饵向着捕食者密度小的方向移动。当d4>0时，-d2d4v▽u反应了食饵形成一个团结互助、共同抵御捕食者的群体。在现实生态环境中，捕食与自我防御行为是经常发生的。

本文主要研究模型(1)的共存性。首先，给出正解的先验估计；其次，利用拓扑度理论得到非常数正解的存在性。需要说明的是，本文中给出的非常数正解的存在性条件(见定理3)恰好为文献[9]中给出的非常数正解的不存在性条件。之所以会出现这样的情形，正是因为我们在文献[9]模型的基础上引入了一个新的交叉扩散项。

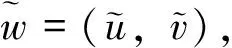
Δ1(a+b)2+4am2-4m1b-4m1m2

在本文中，将沿用文献[9]中的记号：

a2(b)

1 解的先验估计

本节主要给出模型(1)的非常数正解的上界和下界。为了方便，记Λ=Λ(a,b,m1,m2)。

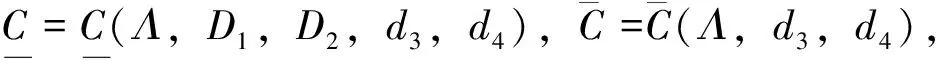
其中D1,D2为给定的正常数。

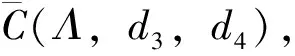
(2)

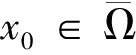
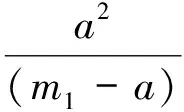
因此，

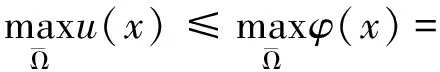
[1+d3v(x0)]u(x0)≤(1+d3M)aC1

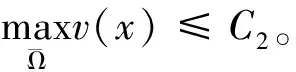
首先证存在C*=C*(n,Ω,Λ,D1,D2,d3,d4)，使得

(3)

由模型(2)和φ=(1+d3v)u，ψ=(1+d4u)v知，问题(1)也可化为

(4)

由上面讨论知

则d1≥D1时，有

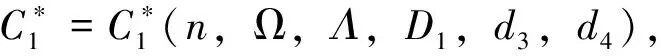
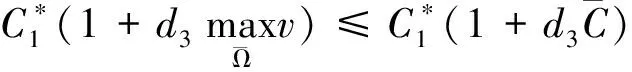
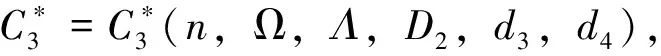
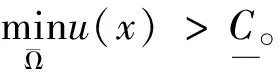
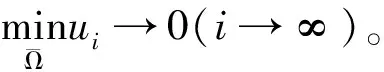
(5)

2 非常数正解的存在性

先给出模型(1)非常数正解不存在的充分条件。

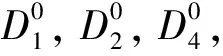
该定理的证明完全类似于文献[15]中的定理4.1的证明，在这里我们从略。

下面运用拓扑度理论证明模型(1)非常数正解的存在性。

设0=μ0<μ1<…是-Δ在齐次Neumann边界条件下的特征值，记

v>0,x∈Ω;∂νu=∂νv=0,x∈∂Ω}

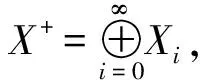
Φ(w)=(d1(1+d3v)u,d2(1+d4u)v)，

w=(u,v)

则系统(1)化为

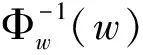
F(w)w-(I-Δ)-1·

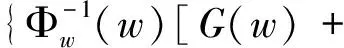
的正解，其中(I-Δ)-1是I-Δ在X+上的逆。由于F(·)是单位算子I的紧扰动，那么对于S，如果对任意w∈∂S，F(w)≠0，则拓扑度deg(F(·),S,0)有意义。计算可得

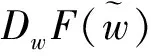
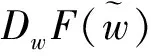
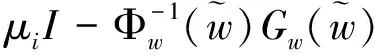
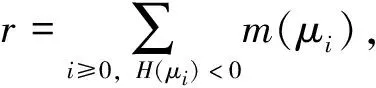
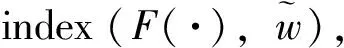
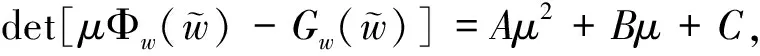
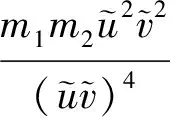
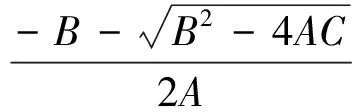
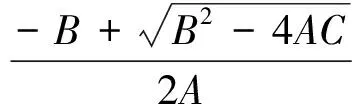
注意到，当B>0时，对应的μ1(d)和μ2(d)为负根。因此，如果μ1(d)和μ2(d)非负且不相等，则A,B,C应满足：B2-4AC>0且B<0，从而有下面引理成立。

引理2 假设B2-4AC>0且B<0。对于给定的μi，i≥0，如果μ1(d)<μi<μ2(d)，那么H(μi)<0，而当μi<μ1(d)或μi>μ2(d)时，H(μi)>0。

下面讨论问题(1)非常数正解的存在性，并假设B<0。

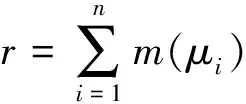
证明因为B<0，所以μ2(d)>μ1(d)>0，且当d2充分大时，

因此存在D2(d1,d3,d4)，当d2>D2(d1,d3,d4)时，有0<μ1(d)<μ1，μ2(d)∈(μn,μn+1)。

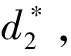
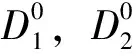
Φ(t;w)=(d1(t)(1+d3(t)v)u，

d2(t)(1+d4(t)u)v)

考虑问题

(6)

显然，w是问题(1)的非常数正解等价于w是问题(6)当t=1时的非常数正解。同时，对任意的t∈[0,1]，问题(6)的非常数正解又等价于下面问题的非常数正解

F(t;w)

[G(w)+▽wΦww(t;w)▽w]+w}=0，w∈X+

(7)

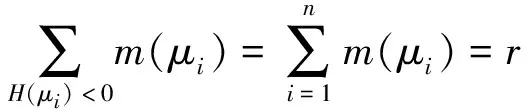
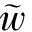
(8)

由定理2知，当t=0时，问题(7)没有非常数正解，且对任意的i≥0，H(μi)>0，因此

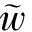
(9)

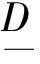
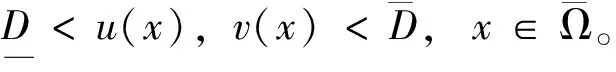
令

则对任意的w=(u,v)∈∂Σ且t∈[0,1]，F(t;w)≠0。由度的同伦不变性知，

deg(F(1;·),Σ,0)=deg(F(0;·),Σ,0)

(10)

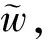
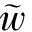
与式(10)矛盾，因此问题(1)存在非常数正解。

3 结 语

本文主要运用拓扑度理论研究了一类新型的具有交叉扩散项的捕食-食饵模型，分析了模型非常数正解的存在性。研究结果表明，当捕食者与食饵的增长率控制在一定范围内时，两物种可以共存。文中所采用的相关研究方法是偏微分方程理论及工具在种群生态学中的具体应用，所得结论对研究具体的生物种群动力学具有一定的现实意义。

[1] SHIGESADA N, KAWASAKI K, TERAMOTO E. Spatial segreation of interacting species [J]. Journal of Theoretical Biology, 1979, 79(1): 83-99.

[2] KO W, RYU K. On a predator-prey system with cross-diffusion representing the tendency of predators in the presence of species [J]. Journal of Mathematical Analysis and Applications, 2008, 314(2): 1133-1142.

[3] KO W, RYU K. On a predator-prey system with cross-diffusion representing the tendency of prey to keep away from its predators [J]. Applied Mathematics Letters, 2008, 21(11): 1177-1183.

[4] WANG M. Stationary patterns caused by cross-diffusion for a three-species prey-predator model [J]. Computers and Mathematics with Applications, 2006, 52(5): 707-720.

[5] OEDA K. Effect of cross-diffusion on the stationary problem of a prey-predator model with a protection zone [J]. Journal of Differential Equations, 2011, 250(10): 3988-4009.

[6] KUTO K. Stability of steady-state solutions to a prey-predator system with cross-diffusion [J]. Journal of Differential Equations, 2004, 197(2): 293-314.

[7] JIA Y, XUE P. Effects of the self- and cross-diffusion on positive steady states for a generalized predator-prey system [J]. Nonlinear Analysis: Real World Applications, 2016, 32: 229-241.

[8] TUOC P V. On global existence of solutions to a cross-diffusion system [J]. Journal of Mathematical Analysis and Applications, 2008, 343(2): 826-834.

[9] ZENG X, LIU Z. Nonconstant positive steady states for a ratio-dependent predator-prey system with cross-diffusion [J]. Nonlinear Analysis: Real World Applications, 2010, 11(1): 372-390.

[10] 王利娟，姜洪领. 带交叉扩散项的捕食模型非常数正解的存在性 [J]. 中山大学学报(自然科学版)，2012, 51(1): 14-18.

WANG L J，JIANG H L. Existence of non-constant positive solutions of a predator model with cross-diffusion [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2012, 51(1): 14-18.

[11] 侯秀梅, 一类带交叉扩散项的食饵-捕食系统的正解的存在性 [J]，中山大学学报(自然科学版)，2008, 47(6): 8-11.

HOU X M. Existence of positive solutions of a prey-predator system with cross-diffusion [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2008, 47(6): 8-11.

[12] PROTTER M H, WEINBERGER H F. Maximum principles in differential equations [M]. Englewood Cliffs: Prentice-Hall, 1967.

[13] LIN C S, NI W M, TAKAGI I. Large amplitude stationary solutions to a chemotaxis system [J]. Journal of Differential Equations, 1988, 72(1): 1-27.

[14] GILBARG D, TRUDINGER N S. Elliptic partial differential equation of second order [M]. New York: Springer Verlag, 1983.

[15] 李艳玲, 李景荣, 郭改慧. 一类具有交叉扩散的捕食模型非常数正解的存在性[J]. 应用数学学报, 2013, 36(2): 230-242.

LI Y L, LI J R, GUO G H. Existence of non-constant positive solutions of a predator model with cross-diffusion [J]. Acta Mathematicae Applicatae Sinica, 2013, 36(2): 230-242.

[16] WANG M. Stationary patterns for a prey-predator model with prey-dependent and ratio-dependent functional responses and diffusion [J]. Physica D: Nonlinear Phenomena, 2004, 196(1/2): 172-192.

Coexistenceforapredator-preymodelwithcross-diffusion

WANGJingjing,JIAYunfeng

(School of Mathematics and Information Science, Shaanxi Normal University, Xi’an 710062, China)

The existence of non-constant positive solutions for a new predator-prey model with cross-diffusion is studied. Firstly, a priori estimate of positive solutions is given. Then, the existence of non-constant positive solutions is given by using degree theory. The result shows that for fixed cross-diffusion coefficients, the predator and prey can coexist when the growth rates of them are controlled in a certain range.

predator-prey model; cross-diffusion; a priori estimate; degree theory; coexistence

10.13471/j.cnki.acta.snus.2017.06.007

2017-04-02

国家自然科学基金(61672021)；陕西师范大学中央高校基本科研业务费专项基金(GK201701001)

王晶晶(1993年生)，女；研究方向偏微分方程理论及应用；E-mail: w785413@snnu.edu.cn

贾云锋(1972年生)，男；研究方向偏微分方程理论及应用；E-mail：jiayf@snnu.edu.cn

O175.26

A

0529-6579(2017)06-0055-05