Numerical simulation of a cabin ventilation subsystem in a space station oriented real-time system

Zezheng QIU,Liping PANG,*,Guoxing LI,Helin ZHANG

aSchool of Aeronautic Science and Engineering,Beihang University,Beijing 100083,China

bAviation Key Laboratory of Science and Technology on Aero Electromechanical System Integration,Nanjing Engineering Institute of Aircraft Systems,Nanjing 211102,China

Numerical simulation of a cabin ventilation subsystem in a space station oriented real-time system

Zezheng QIUa,Liping PANGa,*,Guoxiang LIa,Helin ZHANGb

aSchool of Aeronautic Science and Engineering,Beihang University,Beijing 100083,China

bAviation Key Laboratory of Science and Technology on Aero Electromechanical System Integration,Nanjing Engineering Institute of Aircraft Systems,Nanjing 211102,China

Numerical integration method; Real-time simulation; Stability; THCS; Time-variant system

An environment control and life support system(ECLSS)is an important system in a space station.The ECLSS is a typical complex system,and the real-time simulation technology can help to accelerate its research process by using distributed hardware in a loop simulation system.An implicit fixed time step numerical integration method is recommended for a real-time simulation system with time-varying parameters.However,its computational efficiency is too low to satisfy the real-time data interaction,especially for the complex ECLSS system running on a PC cluster.The instability problem of an explicit method strongly limits its application in the ECLSS real-time simulation although it has a high computational efficiency.This paper proposes an improved numerical simulation method to overcome the instability problem based on the explicit Euler method.A temperature and humidity control subsystem(THCS)is firstly established,and its numerical stability is analyzed by using the eigenvalue estimation theory.Furthermore,an adaptive operator is proposed to avoid the potential instability problem.The stability and accuracy of the proposed method are investigated carefully.Simulation results show that this proposed method can provide a good way for some complex time-variant systems to run their real-time simulation on a PC cluster.

1.Introduction

A space station is a unique laboratory for humans to explore the outer space,1and its environment control and life support system(ECLSS)is one of the important systems because it can provide a basic living environment for astronauts.The ECLSS includes some coupled operating subsystems,such as an atmosphere control and supply subsystem(ACSS),a temperature and humidity control subsystem(THCS),a carbon dioxide removal subsystem(CDRS),a trace contaminants control subsystem(TCCS),a water recovery and management subsystem(WRMS),and a vacuum subsystem(VS).2,3These coupling subsystems are connected by certain fluid pipe networks which are everywhere in the cabin,such as an air ventilation pipe network and a liquid cooling pipe network.4The fluid pipe networks can provide the working pressure and flow rate for components so as to implement flow,heat,and mass transfer or some special chemical reaction processes dynamically.Therefore,correct simulation of pressure- flow coupling performance is the premise of accurate ECLSS dynamic simulation.

Scholars have carried out a lot of research on the dynamic modeling and simulation of ECLSSs.Jones5analyzed the relationship between static and dynamic models,and established an environment simulation system including cabin environment,crew metabolic,and waste management models.Boscheri et al.6built mechanism models for some processes,such as water treatment and carbon dioxide removal and reduction.Their models can reflect the regenerative performance of an ECLSS.The European Space Agency(ESA)developed EcosimPro software to simulate non-regenerative ECLSSs and an electrolytic oxygen process.7Kortenkamp and Bell8set up energy supply and food management models to enrich the ECLSS simulation system.Furthermore,a large number of physical-chemical and biological simulation studies about ECLSSs have emerged in recent years.9–11These studies have promoted the development of ECLSS simulation technology,and played an important role in the research and development of ECLSSs.

Traditional dynamic simulation can put forward constructive opinions about system design and optimization.However,it is not so efficient as to simulate and test dynamic working performance because many high-precision models of subsystems need to be built and calibrated.In this case,the research period is too long to satisfy the requirements of rapid research and development for complex ECLSSs.For this type of complex system,it is urgent to find a new effective way.

Real-time simulation is a very effective way which considers hardware subsystems as virtual simulation models.Hence,hardware models do not need to be built at all,which will obviously save the research period and cut down the research expenditure at the same time.12,13For a complex ECLSS,its real-time simulation system is a very efficient way.

However,the real-time simulation technology has an inherent feature of fixed clock frequency.14The simulation time step should be fixed and set larger enough than the model solution time in each time step.15For this reason,current successful applications of real-time simulation are only some systems with a small number of models,such as some simulations for kinematics behaviors of trajectories16and motion control equations.17There are few real-time simulation applications about the ECLSS of a space station due to the following disadvantageous features.

(1)Coupling relationship between the pressure p and the mass flow rate˙m

In order to solve the values of p andm˙ at any position in a fluid network,it needs to solve all the momentum and mass conservation equations of the flow network together.Hence,the number of equations will be huge if the fluid network system is a relatively complex one.18,19

(2)Time-varying characteristics of model parameters

A change of the valve opening degree will lead to a change of the system eigenvalues correspondingly,which will easily lead to the instability of the simulation system.One way to overcome this issue is to adopt an implicit numerical integration method.

(3)A large amount and various types of subsystem models

An ECLSS includes various components,and their mathematical models include a set of linear or nonlinear differential and algebraic equations.In addition,some models of regenerative components in the ECLSS are complex partial differential equations,such as the models of adsorption beds in the CDRS and the TCCS.In order to obtain their numerical solutions,they need to be transformed into a large number of ordinary differential equations.20

Therefore,the above disadvantageous features will undoubtedly and finally lead to a large amount of ordinary differential equations in the ECLSS simulation system.For time-varying real-time simulation,an implicit fixed time step numerical integration method with a better convergence performance is a preferred way.21However,its computational time in each step is much longer than that of an explicit numerical integration method,especially for a large complex system running on a PC cluster.22The computational time of an implicit method will dramatically increase with an increase of the number of ECLSS models,which cannot satisfy the real-time performance of the system.In contrast,an explicit numerical integration method has a higher computational efficiency in each step than an implicit one,but its simulation result may be not convergent for stiff systems.23If the simulation stability of the ECLSS system can be guaranteed very well,an explicit fixed step numerical integration method will be a good choice to solve a real-time ECLSS simulation system on a PC cluster.24

Oriented to the application of a real-time simulation system on a PC cluster,this paper mainly discuss a simulation method for ECLSSs using an explicit fixed step integral method.A simplified ventilation pipe network in the THCS of an ECLSS is taken as an example to discuss the models and numerical solution.The Gersˇgorin theorem25is adopted to analyze the stability of the large ordinary differential system.By analyzing the eigenvalue distribution of the simulation system,an adaptive operator is proposed to ensure the stability of numerical simulation.Based on the above study,a new modeling method is proposed to ensure the convergence of the system with the explicit numerical integration method.The simplified ECLSS example is used again to explain the application of the new modeling method and the adaptive operator.Furthermore,the simulation stability and simulation error are discussed.The studied simulation method can provide a good way to avoid the numerical divergence problem using the explicit fixed step numerical integration method and ensure the simulation efficiency of a complex real-time system on a PC cluster.

2.ECLSS models

A typical ECLSS distribution of the on-orbit international space station(ISS)is shown in Fig.1(a),which includes a THCS,a CDRS,a TCCS,etc.23The subsystems exchange their mass and heat flows through a ventilation pipe network.In this way,the ECLSS can control cabin air temperature and humidity as well as carbon dioxide and trace contaminant concentrations.A schematic diagram of a simplified ventilation pipe network in a laboratory module is shown in Fig.1(b),which will be taken as an example to discuss the modeling process and the solution method of ill-conditioned linear equations.

The ventilation pipe network of the ECLSS includes many common components,such as fans,pipes,valves,and a condensing heat exchanger(CHE).In addition,it also includes some special components,such as a four-bed molecular sieve(4BMS)in the CDRS and adsorption beds in the TCCS.In this paper,we will study the numerical stability of the ventilation subsystem as shown in Fig.1(b)considering its application in a real-time system.

In the following discussion,we focus on the pressure- flow numerical stability analysis of the time-varying ventilation system using an explicit fixed step integral method.Because of the following two reasons,the influence of a temperature change is considered separately.(A)The eigenvalues of the heat and mass transfer processes are much smaller than that of the pressure process,so the change of the temperature is much slower than that of the pressure.(B)When the change of the temperature is small,its effect on the eigenvalues of differential equations can be ignored,so it has little influence on the stability of the pressure- flow network.

The components in the ECLSS can be generally divided into four types:cabin node,resistance component,pressurization component,and adsorption component.Their models will be introduced as follows.

(1)Cabin node

A cabin node represents the total air in a constant cabin volume.Assume that the cabin air obeys the ideal gas law and mass conservation equation,and then the pressure model of the cabin air can be expressed as26,27

where p is the cabin air pressure,Pa;t is time,s;Rgrepresents the gas constant of atmosphere,J/(mol·K);T is the cabin air absolute temperature,K;V is the effective volume of the cabin,m3;winand woutrepresent the mass flow rates in and out of the cabin,respectively,kg/s.

(2)Resistance component

Some components in the ECLSS can be abstracted as resistance components,such as pipes,valves,the CHE,and adsorption beds.When fluid flows through them,their resistance characteristics will lead to a pressure loss.According to the momentum conservation law,the momentum equation of a pipe can be expressed as26

where pinand poutare the inlet and outlet pressures of the pipe,respectively,Pa;w is the inlet mass flow rate,kg/s;ξ is the pressure loss coefficient;ρinis the fluid density at the inlet of the pipe,kg/m3;A is the cross sectional area of the pipe,m2;wrefis the reference mass flow rate,kg/s;ρrefis the reference density,kg/m3;Δprefis the pressure loss at reference conditions,Pa;nexpis the flow exponent in the user-given pressure loss.R donates an equivalent linear resistance of a resistance component,Pa·s2/kg2.

The mass conservation equation of a resistance component can be divided into two types according to the mass loss term based on whether there exists a mass loss term,that is,

where wdis the mass flow rate removed from the fluid,kg/s,such as the mass flow rate of condensate water in the CHE,the CO2mass flow rate in the 4BMS,and the mass flow rates of trace contaminants in the TCCS.

(3)Pressurization component

Pressurization components can provide necessary dynamic head to circulate the fluid network,such as fans and pumps.The relationship between the pressure difference and the mass flow rate is usually nonlinear.Therefore,their momentum equations can be expressed as26

where g is the gravitational acceleration,9.806 m/s2;h(w)is the total dynamic head at the rated speed,m;Δp0is the total pressure difference on the fan,Pa.

3.Numerical method comparison

Common methods to solve the differential equations in a realtime simulation system are implicit and explicit fixed step numerical integration methods.Hence,the advantages and disadvantages of implicit and explicit fixed step methods will be discussed in detail.

The normalized form of an ordinary differential autonomous system can be expressed as

Explicit and implicit fixed step numerical methods are shown in Eqs.(7)and(8),respectively.

From Eq.(7),we can see that an explicit fixed step method can obtain a solution without any iteration in each step,so its algorithm complexity is O(N)and it has a high computational efficiency.Meanwhile,the solution of an implicit fixed step method at every step has to iterate many times to get a suitable solution,as shown in Eq.(9).Hence,the algorithm complexity of the implicit method is O(N2),so its computational time will increase dramatically with an increase of the differential equations number.

Even though an implicit fixed step method has a better convergence feature,21its computational efficiency is much worse than that of an explicit method,especially for the complicated ECLSS system described by a large number of differential equations.Compared to an implicit fixed step method,an explicit fixed step method has a high computational efficiency in each fixed time step.However,its stability domain is finite,so the explicit fixed step method may face numerical instability problems,which will lead to incorrect results.In order to avoid the instability problems,the system eigenvalue should distribute in the stability domain.

In order to compare the computational efficiency of explicit and implicit fixed step methods,several systems are established with a different number of differential equations.The investigated simulation systems are time-invariant and convergent,that is,the eigenvalues of the systems are in the stability domain no matter for an explicit or implicit method.The Euler method and the backward Euler method are used for comparison,and represent explicit and implicit fixed step numerical integration methods,respectively.By testing in a real-time simulation system on a PC cluster,their computational times at each time step are shown in Fig.2.n is the number of differential equations.Tiand Teare the computational times in a time step by using the implicit and explicit methods,respectively.Conclusions can be drawn from Fig.2 as follows:

(1)For a certain value of n,the implicit method needs greatly more computational time than that of the explicit method,and it is obvious when n is large.

(2)The algorithm complexity of the implicit method is O(N2)while that of the explicit method is O(N).When the number of equations,n,is increased linearly by ten times from 100 to 1100,the computational time at each time step using the implicit method is increased quadratically from 0.11 s up to 18 s.However,the computational time at each time step using the explicit method is increased nearly linearly from 0.54×10-3s to 0.76×10-3s.

Therefore,the implicit method is much more inefficient than the explicit method,especially for a large complex system.The computational time of the implicit method will dramatically increase with an increase of the scales of the ECLSS.The explicit method is a better choice to solve the huge complex ECLSS system than the implicit one.However,the stability of the system should be considered carefully for a time-variant system.The rest of the paper will focus on the stability analysis of the ECLSS simulation system based on the explicit Euler method.

4.Numerical stability analysis and modeling

4.1.Eigenvalue estimation theory

The explicit Euler method is used in the THCS simulation system in this paper.Hence,the distribution of eigenvalues and the absolute stability domain of the Euler method should be studied clearly.23For the explicit Euler method,its stability domain is given as|1+hλ|<1,where h is the simulation time step and λ is the eigenvalue.The stability domain is a closed disc with a radius of 1 centered at point(-1,0)in the complex(hλ)-plane.Only when the system eigenvalues distribute in the stability domain,this system can be stable.

In order to analyze the stability characteristic of an ordinary differential system described by Eq.(6),the Gersˇgorin theorem is adopted to estimate the eigenvalues distribution of the system.28,29The stability using the explicit Euler method is further discussed to solve the THCS simulation models.

4.2.Numerical stability analysis of ELCSS

The function of the THCS is to control the temperature and humidity of cabin air.As shown in Fig.1,in the cabin-pipefan-CHE-valve fluid network,the ventilation fan drives moist air from the cabin to the CHE to realize a mass and energy transfer process.In this way,the air temperature and humidity are decreased,and the condensate water is drained to a water tank.In the following discussion,we use this simplified THCS ventilation network to analyze the numerical simulation stability.As shown in Fig.3,it includes a cabin,a fan,three pipes,a valve,and a CHE.

In Fig.3,w and p denote the inlet mass flow rate and the outlet pressure of the components,respectively,kg/s and Pa.Superscript i(i=1,2,...,6)denotes the ID number of a component.wdrainis the mass flow rate of the condensate water,kg/s.

The momentum equations are as follows:

where wi+1is the outlet mass flow rate of the ith component.According to the mass conservation equations as shown in Eqs.(3)and(4),the momentum equation in Eq.(10)can be rearranged by substituting the outlet mass flow rate of each component,and the corresponding differential system is shown as29

where wdrain=εxliqw5is the mass flow rate of the condensate water,kg/s;ε is the separation coefficient of the water and the vapor;xliqis the mass fraction of the liquid water.

Obviously,the solution of Eq.(10)is the only singularity of the system in Eq.(11).The Jacobian matrix of the differential system in Eq.(11)is shown as follows:

With a change of the valve opening degree,the coefficient matrix J and its eigenvalues will change correspondingly.The valve resistance,R5,increases with its opening degree decreasing.According to the Gersˇgorin theorem,the corresponding eigenvalues in the last row of the coefficient matrix J will decrease de finitely.It is difficult to ensure the eigenvalues of the coefficient matrix J in the stability domain of the explicit Euler method(|1+hλ|<1).

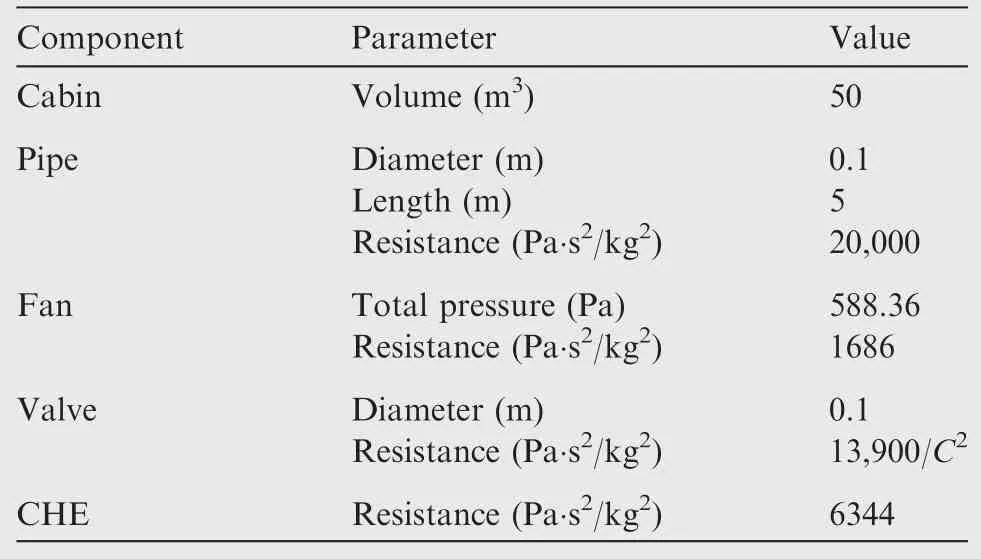
The system eigenvalue curves are shown in Fig.4.When the valve opening degree C is above 20%,the eigenvalues of the system change slightly and keep in the stability domain(-2

4.3.Adaptive operator

According to the numerical stability theorem,21only if the eigenvalues of the coefficient matrix distribute in the stability domain of the explicit Euler method,the system will be convergent and stable.Considering the time-varying characteristic,an adaptive operator,φi,is proposed in this paper to avoid potential instability problems,as shown in the following equation:

The corresponding improved Jacobian matrix of Eq.(12)is shown as follows:

According to the Gersˇgorin theorem,we can estimate that all of the improved Jacobian matrix eigenvalues,hλJ’,are in the closed disc of radius 1 centered at(-1,0).Fig.6 shows the eigenvalue curves of the improved system with changes of the valve opening degree.From Fig.6,we can see that the eigenvalues of the improved system,hλJ’,are kept in the stability domain(|1+hλ|<1)no matter what the valve opening degree is.With the adaptive operator,φi,the convergence and stability of the system can be guaranteed very well.The simulation result in Fig.7 can verify this analysis.The mass flow rate of the improved system converges to 90 g/s in the first ten seconds,and then is stable at 4 g/s when the valve opening degree decreases from 100%to 2%.

Compared with Fig.5,we can draw a conclusion that numerical simulation using the adaptive operator can avoid potential instability problems and keep convergent as shown in Fig.7 when the explicit fixed step Euler method is used to solve the time-variant system.

4.4.Error analysis

In this section,we will discuss the numerical error of the proposed modeling method using the explicit Euler solver.The ECLSS ventilation system as shown in Fig.3 is established in both AMESim25and MATLAB/Simulink.22AMESim is one of the mature commercial simulation software,and its standard solver is a strongly robust and intelligent implicit sol-ver.The solver is composed of some implicit integral methods and can select which one is the optimal integral method intelligently according to the mathematic characteristic of user models.Both of the implicit solver and the component models in the AMESim software have been verified very well.The solution solved in AMESim by its standard implicit solver can be considered as an approximate real solution of the system,but its solution speed is normally slow for a big simulation system.We will use the approximate real solution as the standard for comparisons.

In our study,we will use the explicit Euler solver to obtain the solution of an ECLSS.The test system includes some com-mon components,such as a cabin,a ventilation fan,pipes,a CHE,and a valve.The parameters of the system are listed in Table 1,C denotes the opening degree of the valve,10-5-1.

Table 1 Parameters of simulation system.

From Fig.2,we have known that the computational time of the explicit Euler method can be limited to less than 0.001 s for most systems(n<1100).Therefore,the fixed time step in Simulink can be set as 0.001 s.In addition,a larger time step of 0.01 s is also tested in this study.The valve opening degree decreases from 100%to 2%at 10 s,and it takes 1 s to complete the valve adjustment.The stability performance of the improved model is tested in this way.The mass flow rate response of each component is recorded and analyzed.

The simulation results solved in Simulink are compared with the approximate real solution as shown in Fig.8.In Fig.8,the solid line is the approximate real solution,and the dash-dot line and the dash line are the simulation curves solved in Simulink by the explicit Euler method with time steps of 0.001 s and 0.01 s,respectively.

The results in Fig.8 indicate that:

(1)For the fixed time steps,0.001 s and 0.01 s,their simulation results can converge to the approximate real solution very well without a divergence problem when the valve opening degree is changed from 100%to 2%.

(2)When the valve opening degree adjusts from 100%to

2%,the steady state values of the approximate real solution are 86.4776 g/s and 4.0594 g/s,respectively.Meanwhile,the simulation results of the improved model in Simulink are 86.4783 g/s and 4.0456 g/s.Their relative errors are 0.0009%and-0.3412%,respectively.Hence,the steady-state solution has high numerical simulation accuracy.

(3)The fixed time step will slightly affect the simulation accuracy of the transient process in 10–11 s.There is almost no transient state simulation error when the fixed time step is 0.001 s.When the fixed time step increases to 0.01 s,the transient state error of numerical simulation will increase correspondingly.

In conclusion,this stable simulation method proposed in this paper can solve the instability issue in the time-variant ECLSS simulation system using the explicit Euler algorithm.The simulation result is relatively close to the approximate real solution,especially when the time step is not too big.Its disadvantage is that the transient state error will be affected by the time step slightly.Fortunately,the general transient simulation process is relatively short,and it has a relatively small impact on the whole simulation.

5.Conclusions

This paper mainly studies a simulation method for an ECLSS in space station oriented real-time simulation application.The explicit Euler method is recommended to solve the complex ECLSS system due to its high computational efficiency.To ensure the stability of the system simulation using the explicit Euler algorithm,this paper proposes a stable simulation method to solve the time-variant ECLSS simulation system.Due to the potential instability problem,an adaptive operator deduced by the Gersˇgorin theorem is proposed further.This proposed numerical simulation method can improve the computational efficiency greatly on the premise of ensuring the system stability.Therefore,it provides a good method for some huge complex time-invariant simulation systems to run their real-time simulation on a PC cluster.

In order to introduce this method in detail,a simplified example of ECLSS ventilation pipe network in a space station is used to analyze its stability and explain its modeling method.Based on the study in this paper,the following conclusions can be drawn:

(1)This method supports the explicit numerical method as its solver,so it can satisfy the requirement to conduct a real-time simulation of a complex system on a PC cluster,such as a complex ECLSS simulation system.

(2)The adaptive operator proposed in this paper can ensure the stability of the time-variant system,and avoid the divergence problem of simulation caused by using the explicit fixed time step method.

(3)Based on the adaptive operator,the proposed modeling method can set unified ports for every component,which makes it very convenient to apply this method practically.A uniform interface model for each component can simplify the connection relationship between models and make the simulation convenient.

(4)The steady-state simulation solution is relatively accurate.Though there is a transient state error when the fixed time step is large,it has a relatively small impact on the whole simulation.

Acknowledgement

This work was supported by the Aeronautical Science Foundation of China(No.2014ZC09002).

1.Chen S,Chen J,Jiang G,Liu W.Achievements of manned space program and construction of space station in China.Space Med Med Eng 2012;25(6):391–6[Chinese].

2.Carrasquillo RL.ISS ECLSS technology evolution for exploration.43rd AIAA aerospace sciences meeting and exhibit.Reston:AIAA;2005.

3.Williams DE,Dake JR,Gentry GJ.International space station environmental control and life support system status for the prior year:2010-2011.42nd international conference on environmental systems;Reston:AIAA;2012.p.3162–7.

4.Klingberg T.A stability analysis of the active thermal control system of the Columbus space laboratory[dissertation].Goteborg:Chalmers University of Technology;2011.

5.Jones H.Dynamic modeling of ALS system.33rd international conference on environmental systems.Warrendale:SAE Technical Paper;2003.p.2543–60.

6.Boscheri G,Lavagna M,Lamantea M.Multidisciplinary preliminary sizing of advanced life support systems for space.39rd international conference on environmental systems.Warrendale:SAE Technical Paper;2009.p.2581–93.

7.Pe´rez-Vara R,Mannu S,Pin O,Müller R.Overview of European applications of EcosimPro to ECLSS,CELSS,and ATCS.33rd international conference on environmental systems.Warrendale:SAE Technical Paper;2003.p.2439–48.

8.Kortenkamp D,BellS.Simulating advanced life support systems for integrated controls research.33rd international conference on environmental systems.Warrendale:SAE;2003.p.2546–56.

9.Eckart P.Space flight life support and biospherics.1st ed.New York:Springer;1996.p.1–7.

10.Chang CH,Chan CC,Cheng KJ,Lin JS.Computational fluid dynamics simulation of air exhaust dispersion from negative isolation wards of hospitals.Eng Appl Comput Fluid Mech 2011;5(2):276–85.

11.Mulgundmath VP,Jones RA,Tezel FH,Thibault J.Fixed bed adsorption for the removal of carbon dioxide from nitrogen:breakthrough behaviour and modelling for heat and mass transfer.Sep Purif Technol 2012;85(6):17–27.

12.Viehweider A,Lauss G,Felix L.Stabilization of power Hardwarein-the-loop simulations of electric energy systems.Simul Model Pract Theory 2011;19(7):699–1708.

13.Wolff R,Preusche C,Gerndt A.A modular architecture for an interactive real-time simulation and training environment for satellite on-orbit servicing.J Simul 2014;8(1):50–63.

14.Gonza´lez D,Cueto E,Chinesta F.Real-time direct integration of reduced solid dynamics equations.Int J Numer Meth Eng 2014;99(9):633–53.

15.Ba˘t¸a˘us■M,Maciac A,Oprean M,Vasiliu N.Automotive clutch models for real time simulation.Proc Rom Acad,Ser A 2011;12(2):109–16.

16.Qi ZC,Liu L,Long T,Xing C.The research of trajectory scene Quasi-real-time simulation based on vega prime.J Project Rock Missiles Guid 2013;1:145–55[Chinese].

17.Zebenay M,Boge T,Krenn R,Choukroun D.Analytical and experimental stability investigation of a hardware-in-the-loop satellite docking simulator.Proc Inst Mech Eng,Part G:J Aerospace Eng 2015;229(4):666–81.

18.Ni WD,Gou JB,Sun X.Research on fluid network in thermal power system.J Syst Simul 1997;9(3):78–83[Chinese].

19.Zhou Y,Zhou K,Ma Y,Sui Z.Thermal hydraulic simulation of reactor of HTR-PM based on thermal- fluid network and SIMPLE algorithm.Prog Nucl Energy 2013;62(8):83–93.

20.Liu M,Yang D,Pang L,Huang Y.Experimental and computational investigation of adsorption performance of TC-5A and PSA-5A formanned spacecraft.ChinJAeronaut2015;28(6):1583–92.

21.Bressan N,Carmeli S,Castelli-Dezza F,Iacchetti MF.Numerical integration of ODEs in real-time systems like state observers:Stability aspects.IEEE Trans Ind Appl 2010;48(1):1–7.

22.。Aman R,Handroos H,Eskola T.Computationally efficient two regime flow orifice model for real-time simulation.Simul Model Pract Theory 2008;16(8):945–61.

23.Yang D,Jin T,Wu Z,Zou HF.Dual step size explicit numerical integration method and applications.Power and energy society general meeting-conversion and delivery of electrical energy in the 21st Century.Piscataway:IEEE Press;2008.p.1–8.

24.Macdonald CL,Bhattacharya N,Sprouse BP,Silva GA.Efficient computation of the Grünwald-Letnikov fractional diffusion derivative using adaptive time step memory.J Comput Phys 2015;297(C):221–36.

25.Wu JL,Zhang PP,Wang Y.Numerical methods for determine the equilibrium point’s stability of multidimensional nonlinear dynamic system.Int J Numer Meth Fluids 2011;67(4):531–5.

26.Ecosimpro,environmental and control life support systems library(version 2.2)[Computer Software].EA International;2004.

27.Li K,Liu W,Wang J,Huang Y.An intelligent control method for a large multi-parameter environmental simulation cabin.Chin J Aeronaut 2013;26(6):1360–9.

28.Deu flhard P.A modi fied Newton method for the solution of illconditioned systems of nonlinear equations with application to multiple shooting.Numer Math 1974;22(4):289–315.

29.Wu XY.A numerical method of stiff problems for ill-conditioned linear systems of algebraic equations.Mathematica Numerica Sinica 1999;21(2):157–62.

24 October 2016;revised 20 November 2016;accepted 14 December 2016

Available online 30 August 2017

Ⓒ2017 Production and hosting by Elsevier Ltd.on behalf of Chinese Society of Aeronautics and Astronautics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Corresponding author.

E-mail address:pangliping@buaa.edu.cn(L.PANG).

Peer review under responsibility of Editorial Committee of CJA.