基于超短期风电功率预测的混合储能控制策略研究*

李燕青，袁燕舞，郭通，王子睿，仝年，史依茗

（华北电力大学 河北省输变电设备安全防御重点实验室，河北 保定 071003）

0 引 言

经济社会的快速发展和能源需求与日俱增使风能成为能源结构中必不可少的一部分。随着风电渗透率的不断增大，风电的波动性、随机性和不确定性等问题成为风能迅速发展的瓶颈。储能系统使风电大规模并网成为可能，而由于受到储能机理的限制，尚未出现特性突出、综合能力显著的储能介质，优势结合、缺陷互补的混合储能系统（hybrid energy stor-age system，HESS）将会成为未来储能技术发展的重要方向。

文献［1］提出了基于小波包分解的混合储能控制策略，通过对风机输出功率进行多尺度分解，根据不同储能类型特性分别选择适当的频率范围进行平抑波动，可以在一定程度上优化电池的运行。文献［2］采用小波包分解方法对光伏曲线进行分析，并运用模糊控制对功率型储能的荷电状态进行自适应控制，延长了能量型储能装置寿命。文献［3］提出了一种基于小波变换和双层模糊控制的混合储能控制策略，实现系统功率的修正，自动调整储能设备荷电状态，较好平抑风电功率波动。文献［4］提出了一种基于电池荷电状态分级优化的混合储能控制策略，优化储能装置的荷电状态，有效的避免储能设备的过冲过放。

但是这些控制方法不能够对未来功率变化进行预判，在功率连续变化时容易导致能量型储能装置过充过放，循环次数增加，寿命减少。风电功率准确预测将会对风能的利用有着重要意义。

支持向量机学习方法在解决小样本、非线性和高维数等问题上得到了广泛的应用，广泛应用在风电预测中［5-7］。而核函数参数和惩罚系数的确定将对支持向量机预测模型的优劣产生直接影响。布谷鸟算法是一种新的元启发式算法，可以不用将所有参数寻历一遍就可以找到参数最优解，从而提高了支持向量机的学习能力［8-9］。

在混合储能和风电预测中都会涉及到信号的分解，当前信号分解方法主要有一阶低通滤波、小波分解、经验模态分解等。文献［10］采用了一阶低通滤波原理的风储协调控制策略，但在平抑长期波动时会增大滤波时间常数，增加储能设备负担，经济性较差。文献［1-3，11］提出了采用小波和小波包分解的信号提取方法，但是小波和小波包分解需要事先确定小波基和分解层数，且分解缺乏自适应性。文献［12-14］采用了经验模态分解（Empirical Mode Decomposition，EMD）及其改进的方法对风电信号进行分解和重构，用于风电功率预测，但是该方法的可分辨频率范围有限，特别是对于包含密集模态的多分量信号，EMD会出现模态混叠现象。解析模态分解是Genda Chen等［15-16］提出的一种新的信号分解方法，该方法可以方便的从信号中分离出各个频率成分的信号，但前提是需要确定信号里的各个频率成分，从而确定截止频率值进行AMD分解。AMD目前应用在机械故障诊断［17］、桥梁动态响应［18］等领域，目前尚未应用于电力领域。

本文提出了一种基于超短期风电功率预测的混合储能控制策略，采用AMD分解方法从经过FFT频谱分析的原始信号中提取低频信号，采用改进布谷鸟优化支持向量机惩罚因子参数和核函数参数，进行超短期功率预测，对低频预测信号建立1 min和30 min时间尺度的功率波动分析，判断是否触发蓄电池动作，若动作，首先自适应调整低频预测信号截止频率，然后根据蓄电池荷电状态自适应调整原始风电信号截止频率，有效平滑功率波动，同时减少蓄电池的循环次数，通过模糊控制确定超级电容器补偿的高频信号分量。最后通过MATLAB/Simulink仿真，验证了本文所提方法的有效性。

1 解析模态分解

解析模态分解是一种新的信号分解方法，能够较好的处理信号出现频率混叠、窄带信号以及信号间歇性波动等问题，实现对具有紧密间隔频率分量的信号进行分解，但前提是知道原始信号的频率成分。

若一原始信号y（t）由n个信号分量yj（t）（j=1，2，…，n）组成，如式（1）所示。

式中yj（t）对应的时变频率为ωj（t），则有二分频率ωbj∈（ωj，ωj+1）（j=1，2，…，n-1），可以将原始信号分为两个不同频率信号和，如式（2）所示。

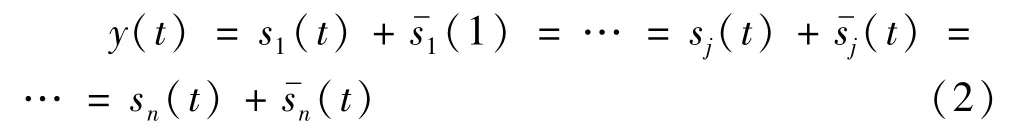
对式（2）进行傅里叶变换，得到如式（3）：

式中sj（t）对应的傅里叶变换分别为，且频率范围分别为｜ω｜＜ωbj和｜ω｜＞ωbj。sj（t）的表达式如式（4）所示。

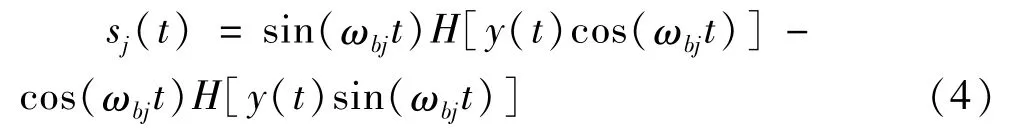
式中H［］为 Hilbert变换；sj（t）是频率小于ωbj的信号是频率大于ωbj的信号。

由式（2）得：

由此便得到了信号y（t）经AMD分解后的两个信号sj（t）和

Feldman［16］进一步对该方法做出新的解释，它可以作为低通滤波器使用。由式（1）可知，如果要提取频率成分为ω（t）＜ω1（t）的信号，只需令截止频率ωb=ω1（t）即可，同理若要提取频率成分为ωj-1（t）＜ω（t）＜ωj（t）的信号，只需分别令截止频率ωb=ωj（t）和ωb=ωj-1（t），将提取的信号相减即可。提取信号原理如图1所示。

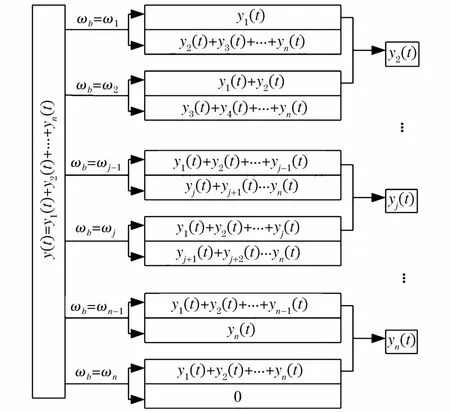
图1 AMD提取信号原理图Fig.1 Schematic diagram of signal extraction using AMD method

根据上述AMD分解原理，设计如图2所示的自适应低通滤波器，从而可以分离出频率低于截止频率的低频信号和高于截止频率的高频信号。

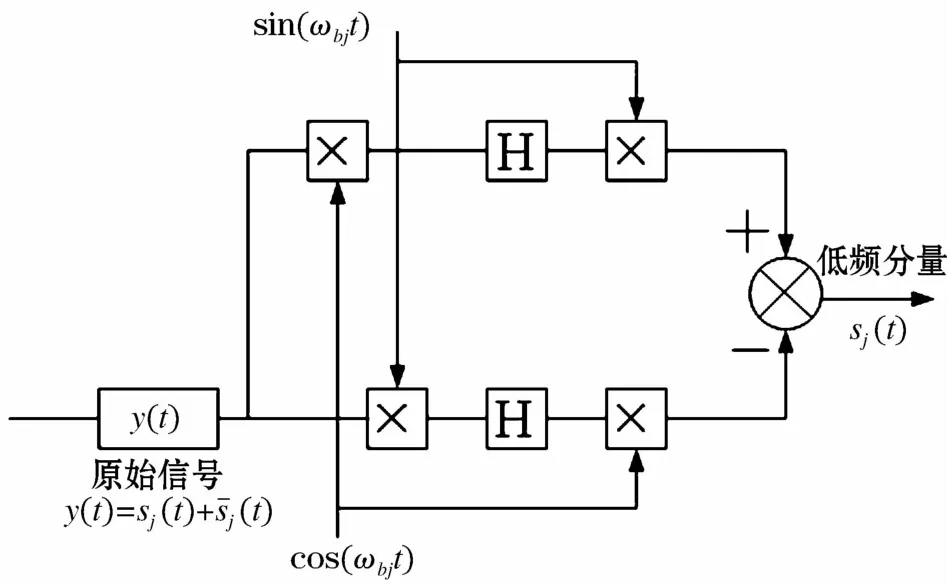
图2 基于AMD分解的时频低通滤波器框图Fig.2 Block diagram of a time-frequency low pass filter with AMD method

2 基于改进CS优化SVM的超短期风电功率预测

由于篇幅限制，本文不过多介绍支持向量机理论，由文献［13］可知，在使用SVM进行风电功率预测中，惩罚因子参数C和核函数参数σ2的确定尤为重要，CS算法是一种采用飞行的搜索方式，既可以加快局部搜索效率，又可以确保系统不会陷入局部最优解，是一种有效的寻优方法。标准CS算法需做如下假设：（1）每只布谷鸟每次只产一个蛋，随机放入某个鸟窝；（2）存有布谷鸟蛋最好的鸟巢将会保留到下一代；（3）鸟巢数量为确定值n，且布谷鸟蛋被发现的概率为固定值Pa。详细介绍见文献［8］。

为了进一步提高CS算法的寻优效率和寻优精度，本文从以下两个方面进行改善：

（1）自适应动态调整控制策略

由于CS算法寻优路径采取随机游走策略，步长大小不定，步长较大时，可以保证搜出全局最优解，但其搜索精度会降低；步长较小时，搜索精度提高，但会降低全局最优搜索能力。为此，我们可以根据适应值f的不同，自适应动态采用不同的控制策略，使搜索速度和搜索精度同时提高。具体策略如下：

1）设某一代中，规模为n的群体的平均适应值为fa=（f1+f2+… +fn）/n，最差个体的适应值是fworst。然后将优于fa的鸟巢的适应值求平均得到f′a。将种群分为fi＜f′a、f′a＜fi＜fa、fa＜fi三组，分别对每组采用不同的控制策略进行更新；

2）将适应值fa＜fi的鸟巢归为第一组，其所对应的步长控制向量分量更新如式（6）所示；

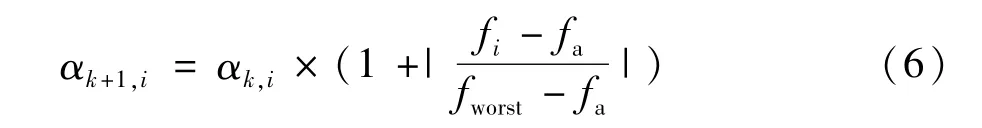
3）将适应值f′a＜fi＜fa的鸟巢归为第二组，其所对应的步长控制向量分量保持不变；

4）将适应值fi＜f′a的鸟巢归为第三组，其鸟巢的个数为N1，其对应编号记作k=1，2，…，N1，由于该组鸟巢较为接近最优解，本文对该组鸟巢引入混沌扰动算子，以提高算法的搜索精度。其计算方式如式（7）。

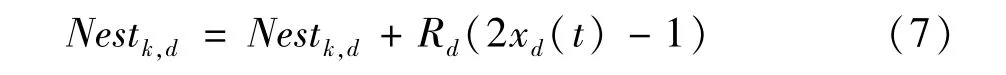
式中Nestk，d为当前第三组鸟巢位置的第d维向量值；Rd为当前鸟巢位置的第d维位置混沌扰动搜索区域半径；xd（t）为当前代产生的混沌序列，见式（8）。

混沌序列产生方式如下：

（a）随机产生D维向量xi=（xi，1，xi，2，…，xi，D），其中每个分量的值为（0，1）之间的随机数；

（b）为了产生具有较高随机性和遍历性的混沌序列，本文采取kent混沌映射系统，如式（8）。

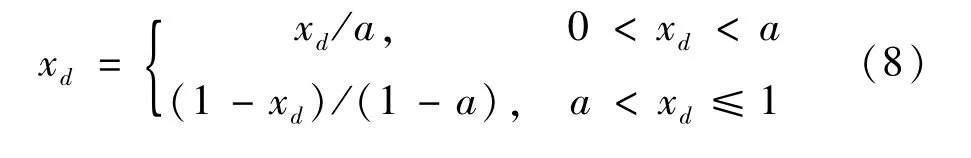
式中a=0.4。通过式（8）进行T次迭代，产生混沌序列，计第j次序列为x（j）=（x1（j），x2（j），…，xD（j））。

（c）由于在多维函数的寻优过程中，各维数值各不相同，本文采用逐维变化混沌扰动的方式确定其混沌扰动的半径，如式（9）。

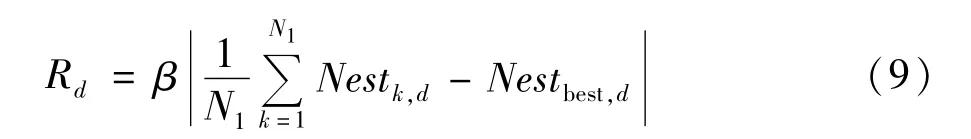
式中β为比例系数为当前代第一组鸟巢位置的第d维变量的平均值；Nestbest，d为当前代鸟巢位置的第d维变量的最优值。

（2）引入动态发现概率

引入布谷蛋动态发现概率代替固定发现概率，使得算法在搜索后期更多的产生新个体，有效避免产生局部最优解。随着寻优质量的逐步提高，适当增加发现概率Pa，使得在进化后期越容易产生新的个体，避免算法陷入局部最优解。本文采用正弦递增策略实现Pa的动态变化，如式（10）所示。

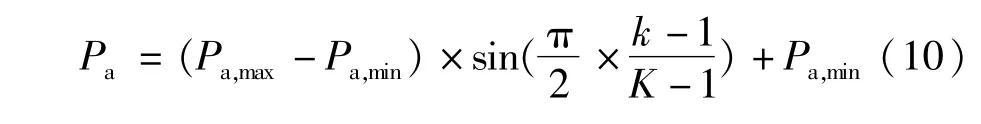
式中K为算法的最大进化代数；k为当前进化代数；Pa，max和Pa，min为Pa的控制参数。

3 蓄电池动作判断标准

由于蓄电池价格昂贵，循环寿命有限，为了减少蓄电池循环次数，本文设定蓄电池动作标准如下：

首先，按的Δt=1 s时间间隔对低频预测功率数据进行划分。设风电额定功率为Prate，从第i秒开始，确定（i-59）秒～i秒时间段内风电功率的最大值Pi，max和最小值Pi，min以及第i秒风电功率Pi。

本文定义第i秒风电功率1min时间尺度功率波动率数学表达式如下：

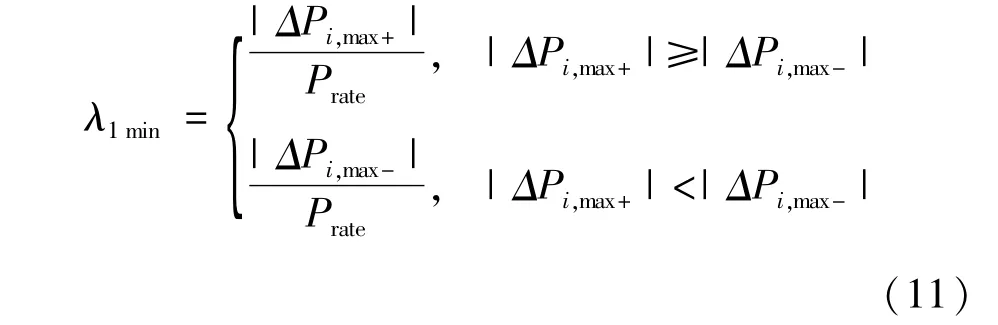
式中ΔPi，max+=Pi-Pi，min；ΔPi，max-=Pi-Pi，max。同理可以定义风电功率30 min时间尺度功率波动率λ30min。

λ值越小，则说明并网功率平滑度越好；λ值越大，则并网功率波动越大。储能系统容量配置不同时，能够补偿的风电功率波动也不同，故λ1min和λ30min的取值需根据实际系统进行调整。

设1 min和30 min尺度功率波动要求分别低于γ1和γ2，若1 min和30 min尺度功率波动满足要求，则蓄电池不动作；若未能满足功率波动要求，则需触发蓄电池动作，此时自适应调整低频预测分量AMD分解截止频率ωb2，判断是否满足1 min和30 min尺度功率波动要求，若不满足，则继续减小截止频率直到满足为止；若满足，则确定最终低频预测分量AMD分解截止频率ωb2，从低频预测分量中分别提取出较低频分量和较高频分量，较低频分量直接并网，较高频分量作为蓄电池的初步补偿功率指令Pb。

4 蓄电池荷电状态自适应调整AMD截止频率

蓄电池运行时间较长时，其容量较容易达到上下限，将会直接影响下一刻风电输出功率的平抑效果。故本文根据蓄电池荷电状态SOCb和充放电功率指令，自适应调整原始风机出力AMD分解的截止频率ωb1，间接使蓄电池SOCb维持在合理范围内，设Pb＞0时为充电状态，Pb＜0时为放电状态，蓄电池正常工作的荷电状态上下限为，极限条件的荷电状态上下限为

具体控制策略如下：

自适应调整原始风机出力AMD分解截止频率ωb1的流程图如图3所示。

超级电容器初步补偿功率指令为风机实际出力减去低频预测出力，由模糊控制进行调节，具体介绍见文献［2］。

5 混合储能充放电总体策略

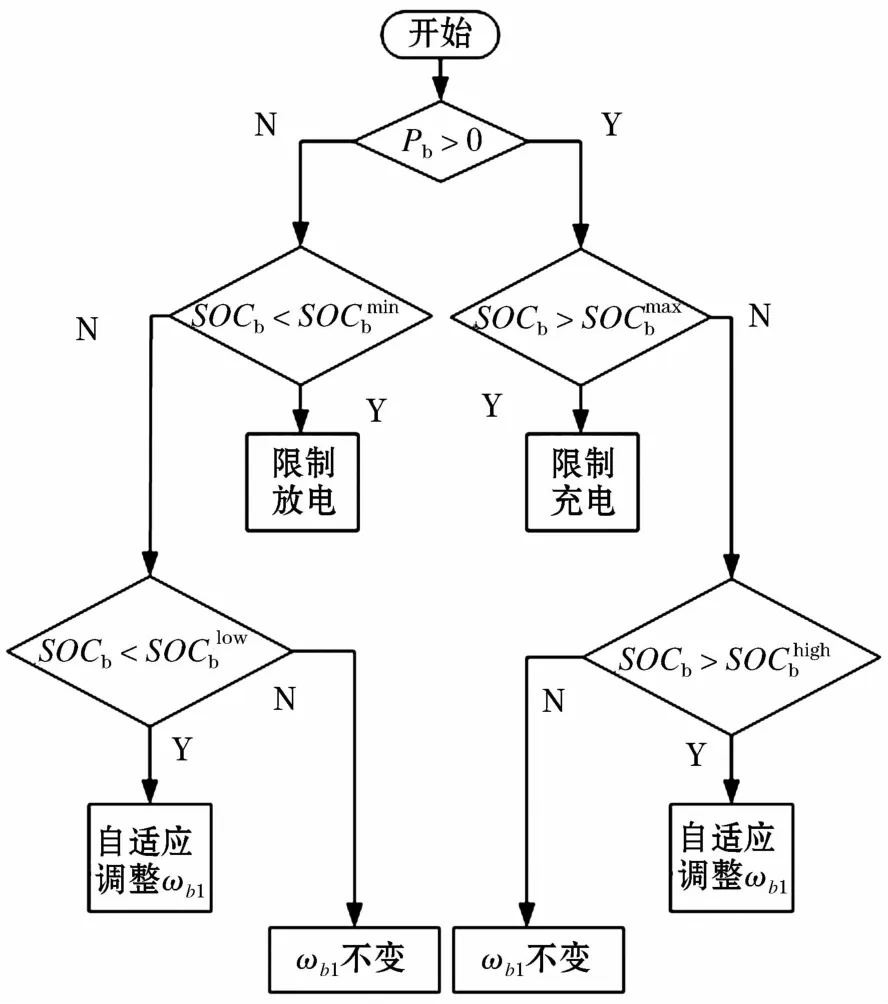
图3 自适应调整截止频率流程图Fig.3 Flow chart of self-adaptive adjustment of the cut-off frequency

本文首先使用FFT对原始信号进行频谱分析，对原始风机出力信号进行AMD分解，根据需求得到低频分量；其次对低频分量采用改进布谷鸟优化SVM的惩罚因子参数和核函数参数，进行超短期功率预测；再次定义了蓄电池动作判定标准，判断蓄电池是否动作，若动作，调节低频预测信号的截止频率，直到满足并网要求，从而确定蓄电池补偿功率指令；最后根据蓄电池荷电状态和补偿功率指令自适应调节原始风机出力截止频率，从而有效保护蓄电池，延长蓄电池使用寿命，对超级电容器补偿功率指令采用模糊控制进行调节。

总体控制流程图如图4所示。

6 仿真算例

以内蒙古某99 MW风电场为例，本文采集了该风电场2014年全年实际输出功率数据，采样时间间隔为1 s，设定γ1为0.02，γ2为0.1，蓄电池容量配置为10 MWh，超级电容器容量配置为2.5 MWh，蓄电池初始荷电状态为0.5，超级电容器初始荷电状态为0.5，为 0.8为 0.2，为0.9，为0.1。

对采样数据进行快速傅里叶变换，得到如图5所示的幅频特性曲线。

由图5可知，风电功率能量主要集中在低频部分（0 Hz～10-3Hz），高频部分能量较低，由超级电容器补偿。故ωb1和ωb2初始值为10-3Hz。从全年数据中提取7 200个采样点，采样时间为2 h，通过AMD分解，可得如图6所示的各分量处理情况。

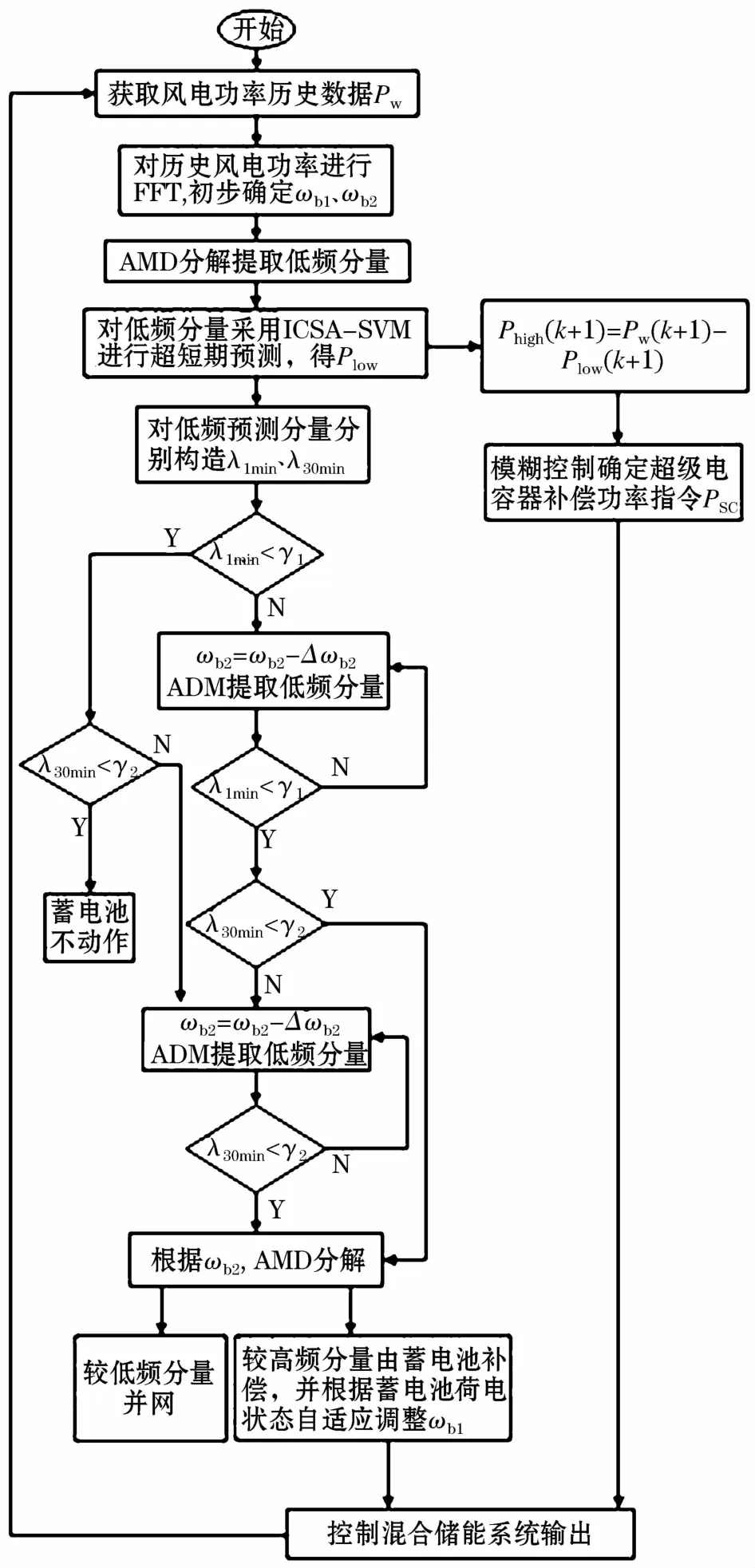
图4 混合储能总体控制流程图Fig.4 Overall control flow chart of hybrid energy storage

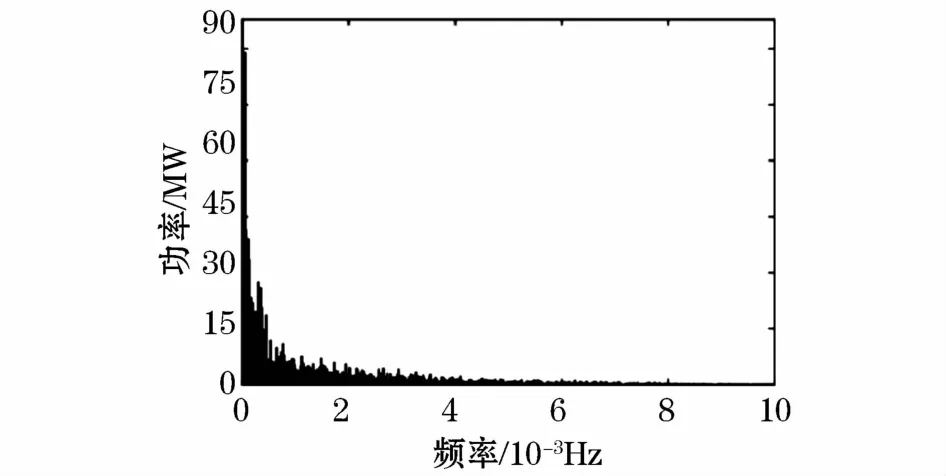
图5 某99MW风电场全年风机出力幅频特性曲线Fig.5 Curve of amplitude frequency characteristics of wind power in the whole year at a 99 MW wind farm

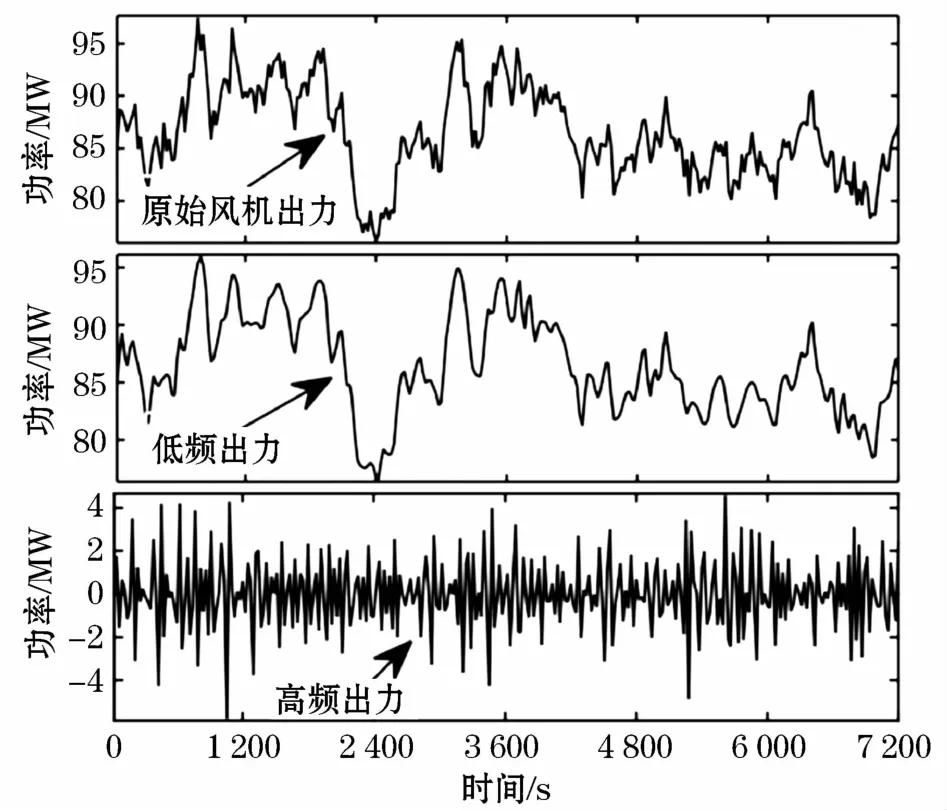
图6 基于AMD分解的风机出力各分量出力图Fig.6 Output diagram of wind turbine output based on AMD decomposition

6.1 超短期风电功率预测

从以上低频功率信号中采样300组数据，采样间隔为24 s，选取前275组数据，其中前250组数据为训练样本，后25组数据为测试样本，构造SVM预测模型，对低频分量进行建模回归和预测。设鸟巢数为30，最大迭代次数为40，最大发现概率0.65，最小发现概率0.20，SVM核函数选择为高斯径向基函数，其参数σ2搜索范围为10-5～105，惩罚因子参数C搜索范围为10-5～105。对数据归一化处理后，分别对采用布谷鸟算法优化SVM参数（CSA-SVM）和ICSA-SVM通过MATLAB平台仿真进行对比分析，并采用均方根误差（RMSE）、平均绝对误差（MAE）对两种分析方法进行评价，其对应公式如式（12）、式（13）所示。

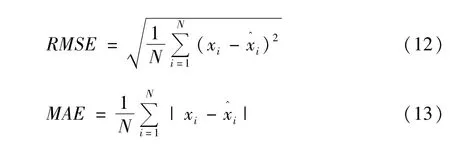
式中xi为功率实际值；为功率预测值；N为样本数。

通过仿真，得到分别采用两种不同方法寻优参数时的风电功率低频分量预测对比如图7所示。

两种预测模型预测评价指标和收敛时间对比如表1所示。

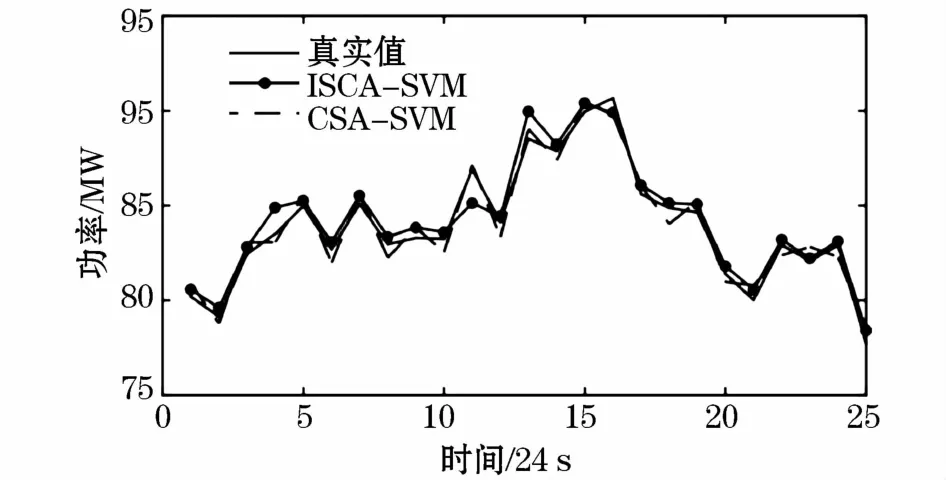
图7 采用两种方法寻优时风电功率低频分量预测对比图Fig.7 Comparison chart of using two kinds of optimization methods for low frequency of wind power prediction

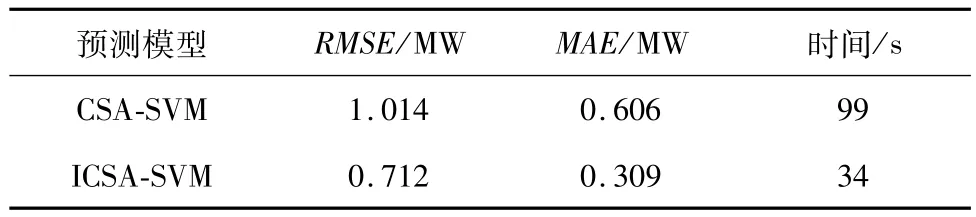
表1 采用两种方法风电功率预测指标对比Tab.1 Comparison of wind power prediction indexes using two methods

由图7和表1可知，采用ICSA-SVM方法的风功率预测模型能够得到较好的预测效果，收敛时间大大减小，故本文采用ICSA-SVM进行超短期风电功率预测和混合储能控制。

6.2 混合储能平抑并网功率波动

对低频分量进行超短期风电功率预测以后，分别对预测分量未来2 h时段的1 min和30 min功率波动情况进行分析和控制。图8和图9分别为未来2 h时段内采用本文控制策略前后的1 min和30 min功率波动对比图，由图可知，改善前有一部分功率波动超出了蓄电池动作标准，根据流程图调整，功率波动率都可以满足并网需求。

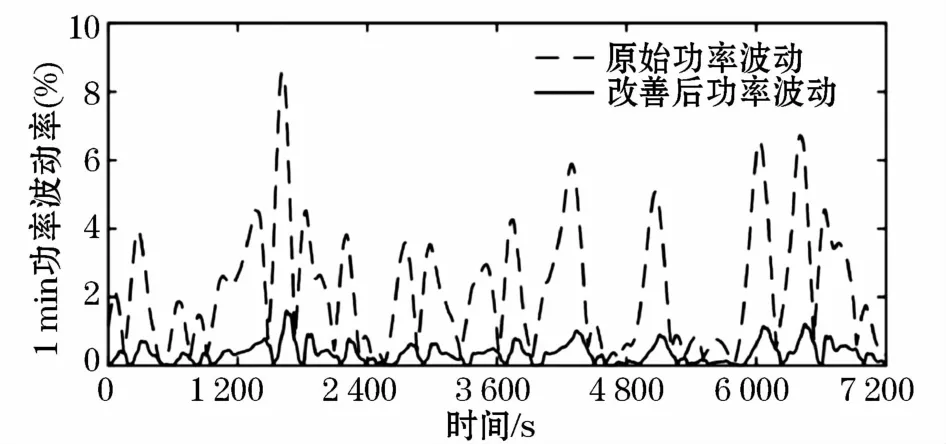
图8 1 min功率波动改善前后对比图Fig.8 Contrast diagram of power fluctuation of 1 min before and after improvement

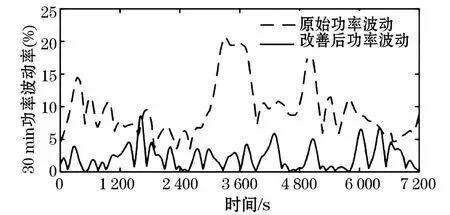
图9 30 min功率波动改善前后对比图Fig.9 Contrast diagram of power fluctuation of 30 min before and after improvement

已知，即可确定蓄电池初步补偿功率，根据蓄电池荷电状态自适应调整，可得蓄电池最终补偿功率。图10为采用蓄电池荷电状态自适应调整前后的蓄电池补偿功率和荷电状态对比图，由图8、图9和图10可知，根据低频分量功率波动判断是否触发蓄电池动作，可以大大减少蓄电池的循环次数。由图10可知采用蓄电池荷电状态自适应调整截止频率可以有效的防止蓄电池过充过放，保护蓄电池，延长蓄电池寿命。

图10 蓄电池补偿功率和荷电状态改善前后对比图Fig.10 Contrast diagram of compensation power and SOC of battery before and after improvement

图11为超级电容器采用模糊控制前后的SOC对比图，由图11可知，通过模糊控制，可以有效防止超级电容器过充过放，使超级电容器在正常状态运行。

7 结束语

（1）通过引入解析模态分解，可以有效地解决小波分解需要事先确定小波基和分解层数、经验模态分解出现模态混叠以及一阶低通滤波增大滤波时间常数，增加储能设备负担的问题；

（2）提出了一种改进布谷鸟算法，通过引入自适应动态调整控制策略和动态发现概率，提高算法的寻优速度和寻优精度，仿真结果表明ICSA-SVM比CSA-SVM收敛速度大大提高，且能得到很好的预测效果；

（3）对低频预测功率根据1 min和30 min时间尺度功率波动来判断是否触发蓄电池动作的控制策略，可以有效的减少蓄电池循环次数，延长蓄电池寿命；

（4）根据蓄电池荷电状态自适应调整原始风机出力AMD截止频率，可以有效的防止蓄电池过充过放，延长蓄电池寿命；对超级电容器采用模糊控制可以有效的使超级电容器在正常状态运行。