银行ATM设备业务总量的时序特征分析及预测
韦金香, 张建同
(同济大学 经济与管理学院,上海 200092)
银行ATM设备业务总量的时序特征分析及预测
韦金香, 张建同
(同济大学 经济与管理学院,上海 200092)
本文旨在分析银行ATM设备业务总量的时序特征,并据此对其进行预测。首先,本文以十分钟为间隔,绘制了银行ATM设备业务总量的30天趋势图,发现其以日为单位,呈现出显著的周期性、扰动性和多峰性,因此本文建立了以日为周期的ATM设备业务总量时序分布模型。在求解模型的过程中,本文利用模拟退火算法将每日银行系统ATM设备业务总量按其特征分为八段,消除了业务总量时间序列的多峰性。在此基础上,建立了Holt-Winters模型对业务总量进行预测,最后用第一时段进行验证,得到95%置信区间内的预测值。本文的研究结果为银行数据监控中心判断设备运行状态提供了依据。
时序分布模型;模拟退火;Holt-Winters模型;运行状态
关于时间序列应用问题,多用于以下方面:(1)降维,寻找序列特点;(2)聚类,在聚类结果上进行分析;(3)预测。银行ATM设备业务总量数据具有时间序列特点,序列形状复杂但具有规律,本文运用时间序列的思考方式对银行ATM设备业务总量的特征进行分析,并预测其正常状态下的数值,从而对各行自助设备运行情况进行判定。
1 ATM设备业务总量的时序建模
1.1 样本数据基本特征
因为银行ATM设备业务量是时间序列,因此,首先应判断该序列是否能够进行预测,才能够进一步通过建立模型判定设备运行状态。因此本文建立业务量的时间序列自回归方程,利用MATLAB进行平稳性检验,得到其显著水平为0.1%,因此通过5%的显著性水平检验,判定业务量时间序列符合平稳性的特征。
随后,利用R软件初步画出样本数据的趋势图,由此判断业务量时间序列的趋势性和周期性,如图1所示。
其中第一行为原业务量图,第二行为幅值表征趋势变化图,第三行为周期性,第四行为随机扰动。从图1中可以清晰看到数据以天为周期,呈现明显的周期性和趋势性,扰动分布规律不明显。
确定ATM设备业务量以天为周期,本文进一步画出以天为单位周期的图像,如图2所示。

图1 ATM设备业务量趋势图
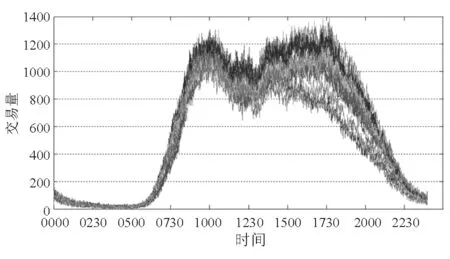
图2 ATM设备每天变化趋势图
从图2中可以看出,ATM设备业务量在时序上呈现非均质特征,业务量所构成的时间序列具有多峰值和周期性。因此,需针对业务总量的时序特征,阶段性、周期性地建立准确的ATM设备业务访问预测模型。
1.2 ATM设备业务总量的时序分布模型
上文提及ATM设备业务总量具有以天为周期的性质,但一天内业务总量具有多峰性,因此应当进一步将其以天为周期,探究其阶段性特征。而分行上传的每个时刻的业务量是一个根据时间变化的源源不断的随机过程,所以在对其进行阶段性研究时应当将业务量作为一个时间序列进行分析,考虑业务量变化及正常范围时不应该将其与时间分离。对于ATM应用系统,将一个周期T(天)内的时间分为n等长时段L(s,t)={S(t1),S(t2),…,S(tn)},其中S,t分别为分行业务量的业务量因子和时间因子。
本文研究其在不同时间段的特征,就是在研究按序(时间排列)将全部样品(业务量)截成几段,同类样品(业务量)次序互相衔接的问题,即可以归纳为有序分类问题,符合Fisher最优分割思想。
本文研究需要从ATM应用系统业务量时间序列L(s,t)={S(t1),S(t2),…,S(tn)}中发现分行ATM应用系统业务量的模式T={T1,T2,…,Tk},其中Ti(1≤i≤k)在时间上相连接。其中,由于以天作为周期,而不同日期具有不同特征,所以本文将样本数据研究天数(共p天)作为指标,记为S(tm)=(dm1,…,dmp),1≤m≤n。
得到一天ATM应用系统业务交易量的时间区间特征:
(1)
利用Fisher最优分割算法划分区间的模型构建是基于算法思想建立的,方法步骤如下:
(1)类的直径
假定分割区间为K类,某一类i业务量区间模式包含时序{S(i),S(i+1),…,S(j)}(j>i),记为G={i,i+1,…,j}。那么该业务量模式的向量均值为:
(2)
设模式内业务量的直径为业务量集的利差平方和D(i,j),则有:

(3)
(2)分类的损失函数

(4)
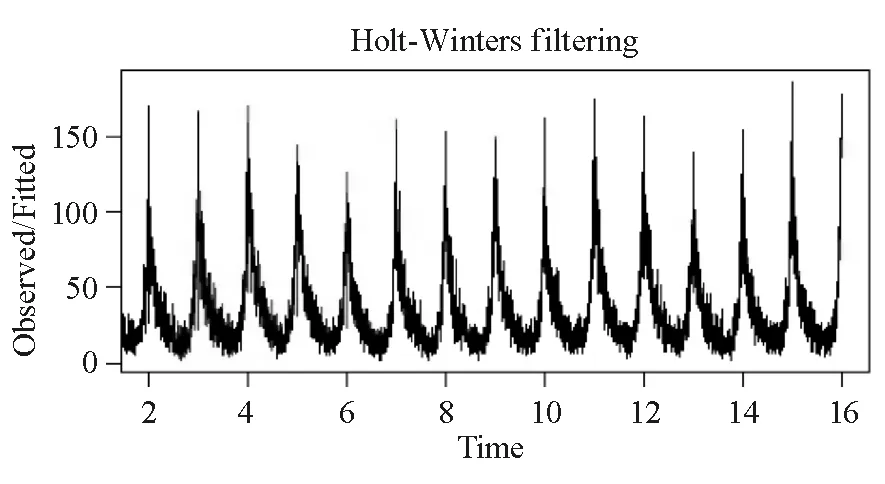
式中分点1=i1 (5) (6) 则通过求解式(6)得到p(n,k)对应的式(4)解,即可得到Fisher最优分割思想下的最优分割点。从而得到式(1)解。 由于ATM应用系统业务量时间序列周期内具有144个时间点,笔者利用求解精确解的思路在计算k=4及以上时,无法计算得到结果。由于业务量以天为周期进行阶段性的分析,对于阶段个数没有精确要求,因此本文采用启发式算法进行求解。由于模拟退火算法(SA)数学模型的描述:在给定邻域结构后,模拟退火过程是从一个状态到另一状态不断随机游动,因此选择SA算法进行求解。 求解过程中,分割阶段数的确定依据Fisher原理:在Fisher最优分割过程中,最小损失函数值随分割k的增加而减少。而当分割数增加到某一数值后,最小损失函数值曲线将急剧变缓,达到一定的平衡,此时的k值为最佳分割值。 训练实验中,对训练样本中业务量数据进行3~12次最优分割,利用MATLAB软件分别得到各次分割下SA算法求得的最小损失函数值,如图3所示。 图3 基于SA算法求解的最小损失函数值变化图 所以,由图3可以得到k=7时为最佳分割取值,并且得到P(n,7)下的ATM应用系统业务量模式所在时间区间,如表1所示。表1显示k值为7时各访问模式的离差平方和值较小。 表1 各业务量模式所在时间区间的集合 表1结果显示,可以将一天内银行系统ATM设备业务总量分为八段,在此基础上进一步预测银行ATM设备业务特征。 上文将一天内的业务总量分为八段,进一步观察分段之后业务总量具有的特点,如图4所示。 图4 00:00~06:39时段业务量月变化趋势 从趋势图中看到,业务量变化具有很强周期性,基于其具有的整体趋势变动性和周期性的二重变化特点,采用加性Holt-Winters模型进行预测(HW模型)。 沙川认为HW模型的基本思想是把具有线性趋势、周期变动和随机变动的时间序列进行分解研究,与指数平滑法相结合,分别对水平项Ut(level)、趋势项bt(trend)和周期项Ft(seasonal component)做出估计,HW模型由以下三个基本公式组成: (7) bt=β(Ut-Ut-1)+(1-β)bt-1 (8) (9) 其中,di为该时段中的观测值,L为该时段周期长度,α,β,γ为对水平、趋势和周期项的平滑参数,取值在[0,1]上,并且使得历史数据满足: (10) 以该月前十五天第一时段数据作为实验数据、后十五天的作为测试数据进行预测,检验HW模型对于ATM业务总量的预测效果。 得到α=0.147,意味着当前预测基于较远的观测值;β=0表明趋势部分的斜率在整个时间序列上是不变的,等于初始值,符合图像的直观感受;γ=0.199表明当天该时段的预测基于较远的观测值。 如图5所示,黑色部分为观测数据,红色部分为HW模型求解得到的前15天实验数据,可见HW算法成功预测了ATM设备业务总量的峰值。于是预测未来2天数据进行比较。 图5 前15天HW模型求解结果 图6 时段1内ATM业务总量预测 其中,图6中蓝色线条表示预测值,深灰色部分表示80%的置信区间,浅灰色表示95%的置信区间。对比实际数据,发现99%实际数据在95%置信区间内,结果合理。因此,可以利用HW模型进行预测,判断未来时段1~8内ATM设备业务总量是否合理,进而判断是否发生故障,及时进行调整。 银行ATM设备总业务量具有周期性和时序性,利用该特征能够判断银行ATM设备运行状况,保证设备正常运行。本文建立银行ATM设备业务总量的时序分布特点,建立时序分布模型,随后利用模拟退火算法对模型进行求解,将业务总量时序分布分为8个时段,进而体现出业务总量分布的多峰值特征;在此基础之上建立简单的加性Holt-Winters模型进行业务量预测,得到95%置信区间内业务总量,当实际数据低于该区间或者高于该区间,说明银行ATM设备存在故障的可能,能够给予银行维护人员警示,保障银行ATM设备交易的正常运行。 现有网络故障诊断方法一般都采用模糊逻辑或概率分析的方法,能够完成不确定性条件下的推理决策,但对于银行网络交易数据而言,其具有较强的时序特征, 因此利用常规的网络诊断方法缺乏针对性。本文通过对ATM设备业务总量时间序列进行建模,按照序列特点采集其特征,并进行业务量预测,从时序特征的角度完成了银行ATM业务总量状态的诊断问题。 在未来研究中,首先,由于模拟退火算法求解结果的精确度较低,因此探究如何准确求解时序模型,将更有利于寻找时序特征。其次,因为数据内容的限制,本文没有考虑ATM设备的状态和地域设置对业务总量的影响,所以未来可集合ATM设备业务总量的时序性和地域性,从而进一步探究银行ATM设备业务总量精确的时空规律,建立更加高效的ATM设备资源时空分配策略。 [1] 冯峥. 基于粗糙集理论的银行卡故障诊断系统研究与实现[D].上海:上海交通大学,2008. [2] 徐定杰,郑笑天. 基于CMDB的银行故障管理优化实现[J]. 黑龙江科技信息,2010(6):70. [3] ESLING P, AGON C. Time-series data mining[J]. ACM Computing Surveys,2012, 45(1):12. [4] 张俊,殷坤龙,王佳佳,等. 基于时间序列与PSO-SVR耦合模型的白水河滑坡位移预测研究[J/OL]. 岩石力学与工程学报,2015,34(2):382-391. [5] BAGNALL A, DAVIS L, HILLS J, et al. Transformation based ensembles for time series classification[C]//Proceedings of the 2012SIAM International Conference on Data Mining (SDM 2012),2012:307-318. [6] BRANDMAIER A M. pdc: permutation distribution clustering[J]. Psychological Methods, 2015, 18(1):71-86. [7] RAKTHANMANON T, KEOGH E. Fast shapelets: a scalable algorithm for discovering time series shapelets. // Proceedings of the13th SIAM International Conference on Data Mining (SDM 2013) .Austin, USA.2013:668-676. [8] 吴华意,李锐,周振,等. 公共地图服务的群体用户访问行为时序特征模型及预测[J/OL]. 武汉大学学报(信息科学版),2015,40(10):1279-1286+1316. [9] 杜涛,熊立华,江聪. 渭河流域降雨时间序列非一致性频率分析[J]. 干旱区地理,2014,37(3):468-479. [10] 钟锦源,张岩,文福拴,等. 基于时间序列相似性匹配的输电系统故障诊断方法[J]. 电力系统自动化,2015,39(6):60-67. [11] 沙川. Holt-Winters时间序列模型参数估计和预测[D].南京:南京大学,2011. ResearchandPredictiononTime-SequenceCharacteristicsoftheTotalBankingAutomaticTellerMachineBusiness (WEIJinxiang,ZHANGJiantong (School of Economics and Management, Tongji University, Shanghai 200092, China) This paper aims to analyze the time-sequence characteristics of the total banking ATM equipment business and predict the number of the business. Firstly, we map the banking ATM equipment 30 days of total trend diagram by taking the data of ten minutes interval. It is found that it has a significant periodicity, perturbation and multi-peak. Then we set up a time-sequence distribution model of total ATM equipment business base on the data of day interval and solve the mode by simulated annealing algorithm (SA). We divided the total amount of ATM equipment of the daily banking system into eight segments according to its characteristics, and eliminating the multi-peak of the total time series of the total business. Finally we forecast the total volume of the business through the Holt-Winters model and use the first period data for verification. And we get the 95% confidence interval of the first period business. The results of this paper provide a basis for judging the operation status of the equipment in the bank data monitoring center. time-sequence distribution model; SA; Holt-Winters model; operation status 2017-10-12 韦金香(1993—),女,广西人,硕士研究生,研究方向为数据挖掘;张建同(1966—),教授,博士生导师,研究方向为应用统计。 E-mail: zhangjiant@163.com。 1005-9679(2017)06-0025-04 F 832 A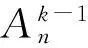
2 基于SA算法的ATM设备业务总量的时序模型求解


3 基于Holtwinters时间序列的业务量预测模型




4 总结

