基于加权多维隶属度函数的软件可靠性模糊评估

毕 翔,吴志雄,刘征宇,陆 阳

(1.合肥工业大学 计算机与信息学院,安徽 合肥 230009; 2.合肥工业大学 机械工程学院,安徽 合肥 230009)

基于加权多维隶属度函数的软件可靠性模糊评估

毕 翔1,吴志雄1,刘征宇2,陆 阳1

(1.合肥工业大学 计算机与信息学院,安徽 合肥 230009; 2.合肥工业大学 机械工程学院,安徽 合肥 230009)

传统软件可靠性预测模型通常把软件视为“黑箱”,仅依据软件测试或实际运行阶段的失效数据来评估,忽略了软件开发过程中的实际影响因素。为此,文章提出一种基于加权多维隶属度函数的软件可靠性模糊评估方法。首先对软件可靠性因素进行分析,并借助粗糙集理论对以上因素进行属性约简,构建软件可靠性的加权多维隶属度函数。该方法可用于对软件开发前、中、后阶段的软件可靠性进行预测和评估。实验结果表明,所提出的方法能够实现对安全关键软件可靠性的准确评估。

软件可靠性;加权;粗糙集;属性约简;隶属度函数

随着计算机软件技术的迅速发展与扩大化应用,整个社会对于计算机系统的依赖日益加深,因软件可靠性带来的计算机系统稳定性问题也急剧上升。同时伴随着软件系统规模的增大及其复杂性的增强,软件系统的可靠性问题更为突出。可靠性作为衡量软件质量的关键指标之一,一直以来缺少有效的实用度量方法[1]。

目前常用的软件可靠性评估方法主要有以下2类:

(1) 以软件可靠性测试阶段所获得的失效数据为对象,在软件内部错误、失效及排除过程的相应假设的基础上,利用数理统计及概率推理等数学工具建立统计分布模型,从而构建基于失效数据的软件可靠性评测模型[2]。目前该类模型多为软件可靠性增长和预测模型,主要包括改进的Jelinski-Moranda 模型[3]、Bayesian推理预测模型[4]等。这类模型一般需要对软件内部错误、失效及排除过程的特性做出相应的假设。然而这些假设都或多或少与软件失效及排错过程的实际情况有所不符,在实际的软件可靠性评估与预测中的准确性不高[5]。

(2) 通过分析软件生命周期中影响软件可靠性的主要因素,例如编程语言、重用代码比例、软件复杂度等,并根据软件特性建立软件可靠性的回归预测模型[6-7]。主要包括基于人工神经网络的模型、基于支持向量机的时间序列回归模型等。该类模型对平稳的失效数据序列具有较高的模型精度,但对非平稳的失效数据有时不尽如人意。

为了进一步提高软件可靠性评估的精度,上述2类构建方法通过引入多维评价因素给出了新的评估模型。但是在分析过程中,这些评价因素的维度及其与模型的相关性阈值,均由研究者根据个人经验判定,由此也带来了新的问题,即受个体认知能力和经验水平的差异,会造成模型输入信息的冗余或损失,前者会降低评估的精度,后者会加重模型的复杂度,从而影响评估结果的稳定性。可以看出,该问题已成为软件可靠性评估方法研究与发展中亟待解决的关键问题。

本文从粗糙集理论和模糊集合隶属度定义出发,通过对软件可靠性因素进行分析,提出了一种基于赋权多特征相似性融合的隶属度计算方法。该方法首先综合考虑软件生命周期中影响可靠性的各种因素,并将软件可靠性视为一个模糊集合,然后借助粗糙集从影响模糊集合的众多特征中约简得到若干重要特征以及重要性,并采用加权欧氏距离计算模糊集合的隶属度函数。在此基础上,提出了基于加权多维隶属度函数的软件可靠性模糊评估方法。通过实验对评估效果进行了验证,实验结果表明,该方法能够显著提升评估性能。同时能够克服小样本集上易出现的过拟合及表现力差的问题,具有较好的稳健性。

1 软件可靠性的影响因素

软件可靠性是关于软件是否能够满足需求功能的性质,实际上软件可靠性在其生命期内受到各种因素的影响,如软件规模、开发环境、可靠性分析技术、软件测试技术、开发人员的能力和经验测试工具、测试人员的思路、风格及经验、不完全排错、运行环境、数据记录误差等[8]。上述可靠性因素都是取自于软件开发过程中的各个阶段,它们都在不同程度上影响着软件的可靠性。因此,可靠性因素与软件可靠性水平密切相关。本文在分析已有研究成果基础上,给出了软件可靠性的综合评估指标体系。该体系首先从4个方面对软件可靠性做出总体评估,接着针对每个方面列出了影响软件可靠性的若干具体因素,具体如下:

(1) 分析和设计类影响因素。包括规格说明的改动、频率、软件设计文档、设计方法、需求分析、详细设计、阶段评价标准、开发环境、开发难度、开发努力程度、开发技术水平、软件规模、软件类别等。

(2) 编码类影响因素。包括程序员技能、高素质程序员的比例、开发队伍的规模、工作压力、应用领域专业知识、开发人员的综合素质、重用代码率、编程语言等。

(3) 测试类影响因素。包括测试环境、测试努力程度、测试方法、测试资源的配置、测试覆盖率、测试工具、测试文档等。

(4) 环境的影响因素。包括处理器、存储设备、I/O设备、运行环境、系统软件等。

2 属性约简

对于软件可靠性因素选取,目前仍没有一种通用的方法。若将所列出的可靠性因素全部作为模型的输入,从实现上看显然是不可行的。而已有的选取方法不可避免地带有个人主观因素,会造成信息冗余或损失。为了从众多可靠性因素中选取一些相对重要的影响因素,本文借助粗糙集和属性约简方法,力图从可靠性因素中约简出若干重要的影响因素以及重要性。受篇幅所限,本文仅介绍与属性约简有关的一些概念。

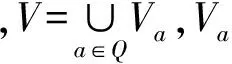
对给定的ε(ε≥0),B⊆C,定义区别矩阵[9]为:

MB={MB(xi,xj)}，

(1)

设DT为一决策表,P⊆C,对x∈U,若∀y∈U,f(x,D)≠f(y,D),有dP(x,y)>ε,则称x在P上是ε-一致对象,属性子集P(P⊆C)上的所有ε-一致对象集简记为U(P,ε)。对给定的ε(ε≥0)和属性子集B(B⊆C),若∀a∈C,则属性a相对B的重要性评价规则为:

Sig(a,B,ε)=|U(B∪{a},ε)|-|U(B,ε)|

(2)

2.1 属性约简算法

所谓属性约简,就是在保持知识库分类能力不变的情况下,删除其中不必要或不相关的属性,目的是找到能区分所有对象的最小属性子集,并用来替代原来的属性集,在一定程度上去掉冗余的条件属性。

基于一致性准则的属性约简(attribute reduction based on consistency criterion，ARBCC)算法是经典粗糙集属性约简的有效推广,它可针对离散或连续值属性进行有效的约简。该算法主要思路[9]如下:

(1) 对给定的决策表,初始化ε,令约简集B=∅,选择一个满足单调性的距离度量函数d。

(2) 计算各属性a的区别矩阵。

(3) 若(C-B)中存在使Sig(a,B,ε)>0最大的属性a,则增加该属性a到B;否则,若对a∈(C-B),Sig(a,B,ε)都为0,则选择使得依赖度(I(MB∪{a})-I(MB))最大的属性a并增加到B。

(4) 重复步骤(3)直到U(B,ε)=U(C,ε)为止。

依据上述一致性准则及相应的属性约简思路,基于一致性准则的属性约简算法具体描述[9]如下。

(1) ∀a∈C:计算区别矩阵Ma;

(2)R=∅;

(3) 计算U(C,ε);

(4) 对∀a∈(C-R),计算Sig(a,R,ε);

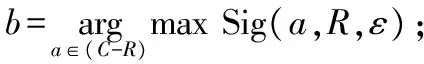
(6) 若Sig(a,R,ε)>0,则R=R∪{b};计算区别矩阵MR; 转至步骤(4);

(7) 若U(R,ε)≠U(C,ε)，则

对∀a∈(C-R),计算I(MR∪{a});

若I(MR∪{b})>I(MR)，则R=R∪{b};计算区别矩阵MR;转至步骤(4);

(8) Return(R).

2.2 确定各种可靠性影响因素权重

依上文所述,本文首先从4个方面对软件可靠性做出总体评估,然后再列出影响软件可靠性的每个方面的若干主要因素。将可靠性因素列为条件属性,把预测软件可靠性作为决策属性。采用ARBCC算法对众多可靠性因素进行属性约简,得到若干重要的可靠因素以及重要性,再对其重要性进行归一化以确定各种可靠性因素权重,具体计算公式为:

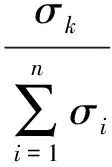
(3)

其中,σi为第k个可靠性因素的重要性;σk′为第k个可靠性因素归一化后的权重。归一化后,可以清楚地知道每个条件属性占决策属性重要性的百分比。

3 软件可靠性模糊评估

软件可靠性模糊评估是基于属性约简和模糊综合原则,将与被评软件可靠性相关的各种因素进行属性约简,得到重要的软件可靠性因素以及相应的权重,并以约简后的软件可靠性影响因素作为输入,构建软件可靠性隶属度函数,从而做出合理准确的评估。本文提出基于多维隶属度的软件可靠性模糊评估方法如图1所示。

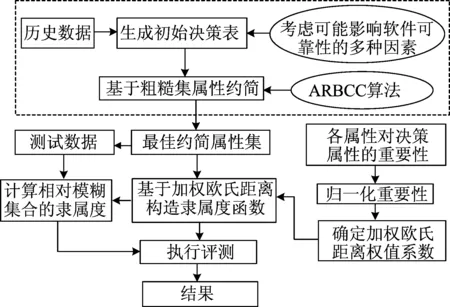
图1 基于多维隶属度函数的软件可靠性模糊评估

3.1 模糊集合代表元素及标准评价距离

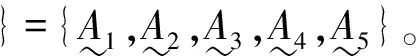
对于不同的事物,可以选择不同的距离函数作为度量标准,一般有欧氏距离、曼哈顿距离、明考斯基距离函数等。其中,欧氏距离函数是最常用的度量方法,其标准化欧氏距离公式[10]为:

(4)

尽管欧氏距离是目前距离度量中常用的方法,但经典欧氏距离无法有效区别样品不同属性之间的差别,不能满足模糊集合特征参照项多样性的实际要求。如果在使用距离函数评价对象间的差异度时,根据特征参照项的重要性赋予不同的权重,那么可以更好地满足模糊集合特征参照项多样性的实际要求。因此,本文以加权欧氏距离替换传统的欧氏距离,其表达式为:

(5)

其中,wj(j=1,2,…,m)为第j个特征参照项的权重。

3.2 新的隶属度函数

构造用于评估软件可靠性的隶属度函数,首要任务是确定其对应模糊集合的代表元素。本文采用加权欧氏距离聚类方法选取代表元素,其中加权欧氏距离函数各属性的权值系数是按照(3)式对各属性重要性归一化得到的。然后根据(5)式的计算方法计算元素x与代表元素的距离,作为元素x到模糊集合的距离,其表达式为:

(6)

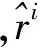
由于模糊集合特征参照项存在着明显的差异,再加上论域上的元素自身存在着多样性,这使得元素到模糊集合的距离可能相差很大,导致无法确定元素与模糊集合的相似性程度。故需要对(6)式得到的距离进行归一化处理。其计算公式[11]为:

(7)

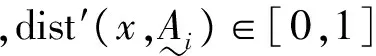
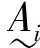
(8)

3.3 软件可靠性模糊评估

根据属性约简算法选取必要的软件可靠性因素以及权重,作为隶属度函数的输入,计算出软件可靠性模糊评估隶属度矩阵C为:

C=[c1,c2,c3,c4,c5]

(9)

其中,c1、c2、c3、c4、c5分别为软件可靠性状态的低、较低、中、较高、高5个等级的隶属度数值。

依据上述矩阵C进行的最终评估所采用的原则是“取隶属度最大项”。在建立模糊规则之后,系统的输出可由输入得到模糊化的结果,如低、较低、中、较高、高,并通过去模糊化获取精确的数值。

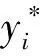
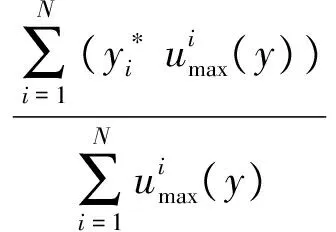
(10)

4 实验结果

4.1 算法的实现

为验证基于加权多维隶属度函数的软件可靠性模糊综合评价的合理性及有效性,本文针对安全关键软件(safety critical software,SCS)进行验证,将32个可靠性因素列为条件属性,把预测软件可靠性作为决策属性,建立初始决策表。同时将待测软件可靠性定义为一个模糊集合,共包括5个级别,即软件可靠性状态={低,较低,中,较高,高}。数据集样本采用美国海军舰队计算机程序设计中心的海军战术数据系统 NTDS和SYS系列数据集[12]。这2组安全关键软件数据集经常被用于软件可靠性定量评估方法性能的比较,具有一定的通用性。

采用ARBCC算法并结合粗糙集相关理论对可能影响软件可靠性的 32个条件属性进行约简,首先要选取一个恰当的一致性参数ε,如图2所示,为了在误分对象数较少的条件下,尽可能使“间隔”取大,取一致性参数ε为0.085。

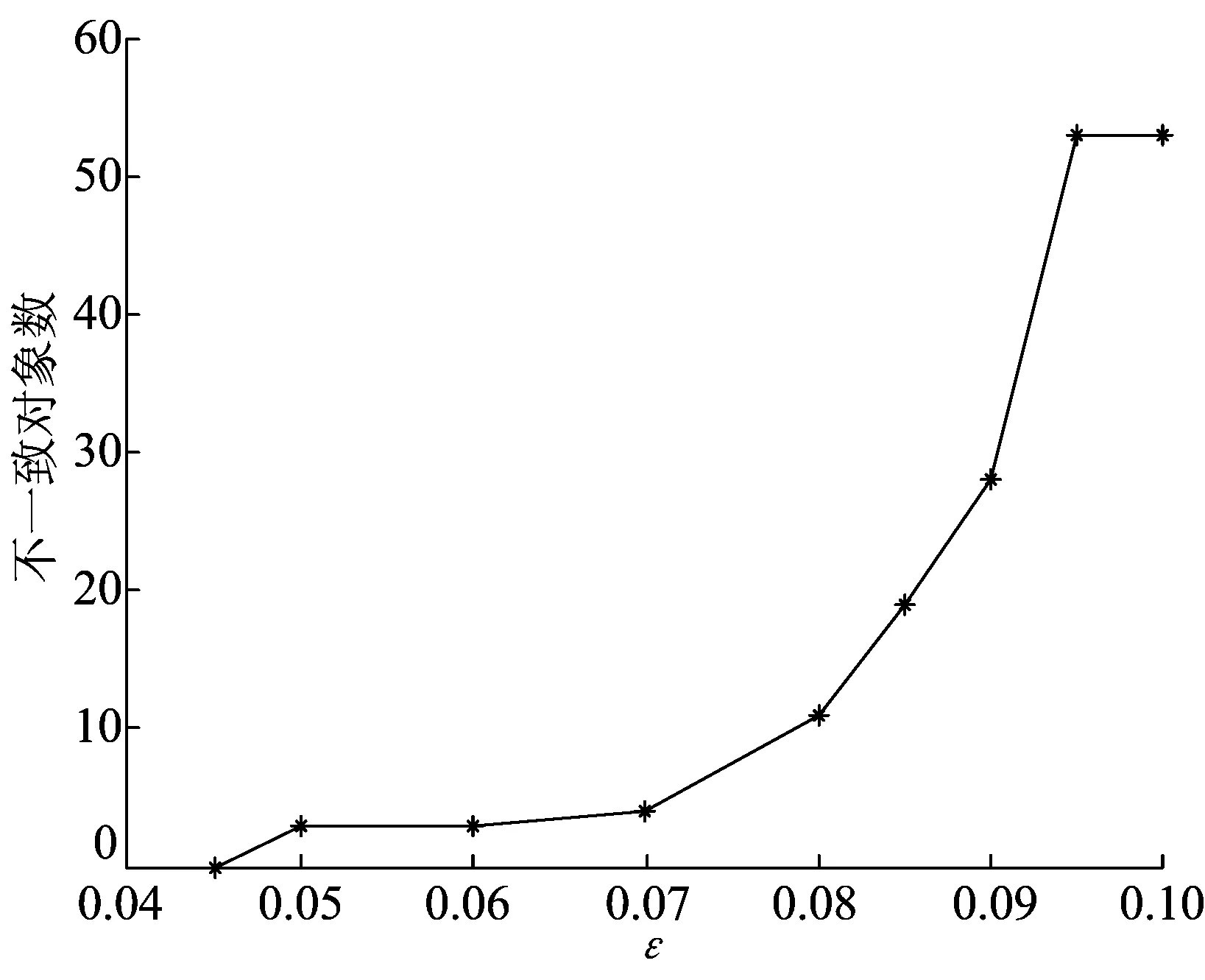
图2 不一致对象数随参数ε的变化

一致性参数确定后,可以对初始的条件属性进行约简。设属性集R的初始状态为空,经过ARBCC算法约简后的属性集R={软件复杂性，程序员的技能，软件测试覆盖率，测试努力程度，软件测试环境，程序规格说明的改动频率}。根据(3)式对属性重要性归一化,结果如图3所示。

图3 约简后条件属性以及重要性

图3中，1为软件复杂性;2为程序员的技能;3为软件测试覆盖率;4为软件测试环境;5为测试努力程度;6为程序规格说明的改动频率。由图3可以看出,软件测试覆盖率对软件可靠性影响最大,而测试工具、详细设计等影响因素并未出现在约简集中。

本文采用基于加权欧氏距离的聚类方法对约简后的历史数据进行聚类,分成相似性较高的5类软件可靠性状态,并得到各类的簇中心,将各类的簇中心分别作为各类软件可靠性状态的代表元素。计算当前对象与各类软件可靠性状态的代表元素之间的加权欧氏距离,再根据(8)式计算出当前对象分别隶属于5类软件可靠性状态程度。然后根据(10)式对输出结果进行去模糊化,得出精确值。

4.2 结果分析

为了验证所提方法的有效性,本文将基于加权多维隶属度函数的软件可靠性模糊综合评价模型与SVM、BP神经网络(BP-NN)进行分类精度方面的比较。在实验中,本文变换训练数据的数量(50～800),测试3种评测方法在测试数据上的错误率如图4所示。

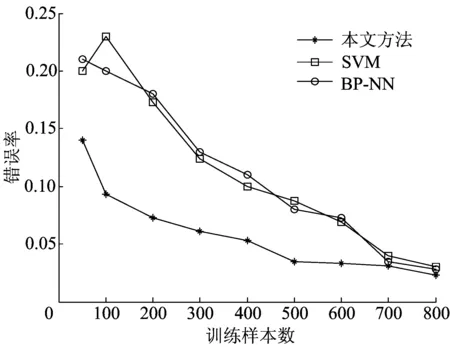
图4 错误率比较

由图4可看出，2种评测方法SVM与BP-NN在这个数据集上比本文方法的错误率大。另外,本文的评测方法受训练样本影响较小,在训练样本很少的情况下能够得到理想的效果。相比之下,SVM与BP-NN评测模型随着训练样本减少,误差上升较快。

分析可知,如果数据集中的数据几何分布是规则的,并且噪声野点很少,则SVM和BP-NN能够表现出良好的检测性能。然而,在现实应用中,数据中往往掺杂大量的噪声或孤立点,则SVM和BP-NN的表现往往很差,由于数据集中的数据几何分布是否规则并不影响本文评测模型的距离计算,因此,本文的评测方法依然能保持良好的检测性能。

5 结 论

可靠性作为衡量软件质量的重要特性,其定量评估和预测已成为人们关注的焦点。本文通过综合考虑软件生命周期中影响其可靠性的各种内在因素,使用粗糙集理论对众多影响因素进行属性约简,在此基础上提出了基于加权多维隶属度函数的软件可靠性模糊评估方法。因为影响因素取自于软件生命周期的各个阶段,能够真实地反映不同阶段软件可靠性受该阶段的影响因素综合影响程度,所以该评价模型可以反映出不同阶段中软件可靠性与该阶段影响因素的关系；这使得该方法可用于对软件开发前、中、后阶段的可靠性进行预测和评估,并根据评估结果及时发现软件开发过程中那些明显影响软件可靠性的因素,及早给予重点关注和纠正,从而达到提高软件可靠性水平的目的。

不仅如此,针对很难收集到失效数据的安全关键软件可靠性的评测,本文提出的软件可靠性预测模型相对于传统软件可靠性预测模型具有的优势更加明显。通过实验分析及算法比较,验证了本文方法的有效性和可行性。实验结果表明,该方法能够显著提升评测性能,明显优于传统的评测方法(SVM和BP-NN)。同时能够克服小样本集上易出现的过拟合及表现力差的问题,具有较好的稳健性。

[1] YANG B,LI X,XIE M,et al.A generic data-driven software reliability model with model mining technique [J].Reliability Engineering & System Safety,2010,95(6):671-678.

[2] MORASCA S.Fundamental aspects of software measurement:software engineering[M].Berlin Heidelberg:Springer,2013:1-45.

[3] TANG Guochun,WU Lihua,LUO Ziqiang.A modification to the jelinski-moranda software reliability growth model based on cloud model theory[C]//Ninth International Conference on Computational Intelligence and Security.[S.l.]:IEEE Computer Society,2011:195-198.

[4] DOGUC O,RAMIREZ-MARQUEZ J E.A generic method for estimating system reliability using Bayesian networks [J].Reliability Engineering & System Safety,2009,94(2):542-550.

[5] 杨晓燕,周远,丁佐华.基于在线故障定位及自主适应提高软件可靠性[J].软件学报,2015,26(4):886-903.

[6] 王金勇,吴智博,舒燕君,等.故障检测率不规则变化的软件可靠性模型[J].软件学报,2015,26(10):2465-2484.

[7] MOURA M C,ZIO E,LINS I D,et al.Failure and reliability prediction by support vector machines regression of time series data [J].Reliability Engineering and System Safety,2011,96(11):1527-1534.

[8] 楼俊钢,蒋云良,申情,等.软件可靠性预测中不同核函数的预测能力评估[J].计算机学报,2013,36(6):1304-1310.

[9] 杨明.一种基于一致性准则的属性约简算法[J].计算机学报,2010,33(2):231-239.

[10] 贡超,蒋建国,齐美彬.基于扩散距离的SURF特征图像匹配算法[J].合肥工业大学学报(自然科学版),2015,38(4):475-478.

[11] 毕翔,韩江洪,刘征宇.基于多特征相似性融合的隶属度函数研究[J].电子测量与仪器学报,2011,25(10):835-841.

[12] 张永强,孙胜娟.基于未确知理论的软件可靠性建模[J].软件学报,2006,17(8):1681-1687.

Fuzzyevaluationofsoftwarereliabilitybasedonweightedmultidimensionalmembershipfunction

BI Xiang1,WU Zhixiong1,LIU Zhengyu2,LU Yang1

(1.School of Computer and Information, Hefei University of Technology, Hefei 230009, China; 2.School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China)

Conventional software reliability predicting models usually regard software as black box, evaluating simply according to software test or failure data of practical running process and neglecting actual influence factors in software development process. For this reason, a fuzzy evaluation method of software reliability based on weighted multidimensional membership function is proposed. Firstly, the software reliability factors are analyzed, and then the attributes reduction of these factors is made by employing rough set theory. Finally, the weighted multidimensional membership function of software reliability is established. The proposed method can be used to predict and evaluate software reliability before, during or after software development. The experimental results show that the proposed method can accurately evaluate the safety critical software reliability.

software reliability; weighting; rough set; attribute reduction; membership function

2016-08-08；

2016-12-23

国家重点研发计划专项资助项目(2016YFC0801405);国家国际科技合作专项资助项目(2015DFI12950)和中央高校基本科研业务费专项资金资助项目(JZ2014HGBZ0004)

毕 翔(1978-),男,安徽黄山人,博士,合肥工业大学讲师,硕士生导师;

吴志雄(1989-),男,安徽枞阳人,合肥工业大学硕士生,通讯作者，E-mail:897415158@qq.com;

陆 阳(1967-),男,安徽合肥人，博士，合肥工业大学教授，博士生导师.

10.3969/j.issn.1003-5060.2017.11.009

TP302.7

A

1003-5060(2017)11-1483-06

(责任编辑 闫杏丽)