封闭容器内部短路燃弧爆炸压力效应计算＊

黎 鹏，阮江军，黄道春，徐国顺，龙明洋，魏梦婷

封闭容器内部短路燃弧爆炸压力效应计算＊

黎 鹏1，阮江军1，黄道春1，徐国顺2，龙明洋1，魏梦婷1

（1.武汉大学电气工程学院，湖北 武汉430072；2.海军工程大学电气工程学院，湖北 武汉430033）

中压开关设备内部短路燃弧爆炸对设备、建筑物以及工作人员的安全带来了严重威胁。为提出合适的数值计算方法对短路爆炸引起的压力效应进行计算，对开关设备内部短路燃弧的能量平衡机制进行了分析；通过分析燃弧过程的热－力效应，提出了基于CFD法的间接耦合分析方法，并开展了实际封闭容器内部短路燃弧实验验证了算法的可行性。研究结果表明：实验测量与模拟计算获得的平均压强仅相差2%左右；电弧尺寸对压力升的影响较小；封闭容器内部压力升随电弧能量的增大近似线性增大；安装负压室后燃弧室的压强可降低60%左右，因此，增设负压室可有效抑制开关设备内部短路爆炸引起的压力升。

开关设备；内部短路燃弧；封闭容器；CFD；压力升

中压开关设备距居民区较近，操作频繁，其安全问题相比其他高压开关设备更应重点关注［1］，特别是内部电弧故障引起的爆炸事故时有发生［2］。据不完全统计，全国平均每年因手车柜电弧短路故障烧毁的开关柜多达200多个［3］；据德国精密机械和电工技术职业协会的事故统计表明，电弧故障引起的事故约占电流事故的25%［4］，可见电弧故障为中压开关设备中不可忽视的一大安全隐患，一旦发生，其产生的高压及高温效应将对工作人员、设备以及建筑物的安全造成巨大威胁［5－6］。

为减少中压开关设备内部短路爆炸事故的发生，国外针对简易小尺寸封闭容器开展了较多数值模拟与实验研究。文献［6－8］中介绍了开关设备内部短路燃弧压力升的多种简化数值计算方法，比较了不同方法的差异，并通过实验与计算分析了简易开关模型内部的压力效应；CIGRE A3.24工作组［9］在假设隔间内压力均匀分布的条件下，提出了简化数值计算模型，对不同介质下开关设备内部短路燃弧引起的压力升进行了计算；文献［10－12］中对封闭容器内部短路燃弧引起的压力升开展了数值模拟与实验研究，分析了热转换系数kp在不同条件下的变化规律。国内针对该问题开展的研究较少，文献［13］针对开关柜内部短路燃弧问题，提出了获得各隔室压力及温度整体分布的简化数值计算方法；文献［14－15］开展了模拟开关柜相间燃弧实验，测量了电弧燃烧过程中柜体内部的压力变化，并对柜体整体的压力升进行了计算。目前，对开关设备内部短路爆炸压力效应的计算，仍以简化算法获得整体的压力变化为主，而对于利用CFD法获得设备内部压力的空间分布缺乏系统研究。文献［16－17］提出的磁流体动力学（MHD）法可建立与实际接近的电弧等离子模型，获得的压力数值精度较高，但计算量较大，对实际开关设备的应用有限。因此，有必要对开关设备内部短路爆炸压力升的计算开展进一步研究。

本文中对开关设备内部短路燃弧的能量平衡机制进行分析，利用L－C振荡回路开展了实际短路燃弧实验，分析短路燃弧故障时的压力及温度效应，据此提出基于CFD的间接耦合分析方法；建立小尺寸简易模型，通过实际封闭容器内部短路燃弧实验对算法的可行性进行验证，并分析相关规律，为后续实际开关设备内部短路爆炸压力升的数值模拟计算提供参考。

1 开关设备内部短路燃弧能量平衡机制

当开关设备内部发生短路燃弧故障时，燃弧功率可达60MW左右，产生的压力升也可达MPa级，电弧释放的能量将以多种机制进行传递；假设电弧释放的总能量为Qarc，电弧在金属电极间燃烧的过程中，弧根与电极之间会发生热传导（Qe），从而使电极温度升高；由于弧根位置的温度可达上万度，在高温作用下，电极与弧根接触部位会出现熔化，并形成金属蒸气携带能量Qmv；同时，释放的金属蒸气会与周围空气发生吸热或放热反应，吸收或释放能量Qchem；电弧释放的热量还会以电磁波的形式辐射至固体壁面（Qrad），使其温度升高；除了上述能量传递之外，大部分能量被周围空气吸收（Qtherm），使空气受热膨胀，从而引起开关设备内部压力上升。上述能量之间的关系可用下式表示：

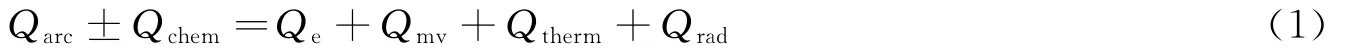
为描述使容器内部压力上升的能量占电弧总能量的比例，系数“kp－因子”被提出［6－7］，其定义如下：

通常情况下，由于式（1）各部分能量很难直接获得，因此“kp－因子”主要通过计算与实验结果的对比来确定［10－11］，kp与气体类型、电极材料、容器尺寸以及气体密度等有关［18］。目前针对设备内部短路燃弧压力升的计算主要基于“kp－因子”，具体表达式为［7－8］：，

该式忽略了压力波的传播特性，假设电弧释放的能量在容器内部均匀分布，且不考虑气体状态的变化。

2 开关设备内部短路燃弧压力升间接耦合计算

2.1 短路燃弧现象

实际开关设备发生内部短路燃弧故障时，由于壳体的影响，很难观察到内部的燃弧现象，因此，为了对短路燃弧过程进行分析，利用电容C与电抗器L振荡提供工频大电流，开展了开放环境下的短路燃弧实验。实验回路如图1所示，包括：SP－铜电极，直径为2cm；CB－合闸断路器，初始状态为分；电压探头HV－测量弧压的大小；Rog－罗氏线圈，用于测量回路电流的大小。铜电极的间距d＝5cm，间隙用焊锡丝短接，当回路接通时，焊锡丝在电流作用下被熔断从而引燃电弧。

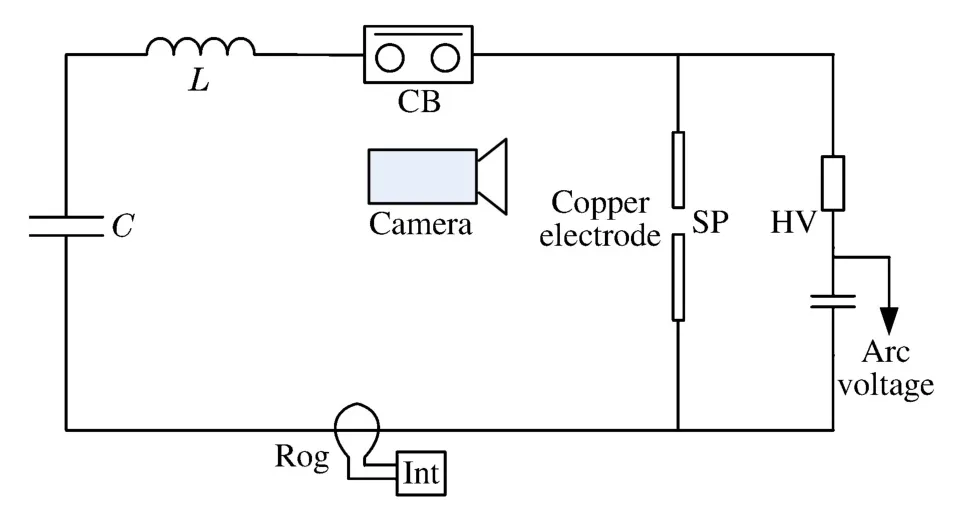
图1 实验布置图Fig.1Diagram of test arrangement

图2 短路燃弧爆炸过程Fig.2Explosion process of short－circuit arcing

短路燃弧爆炸现象如图2所示，整个燃弧过程仅持续50ms，其中电流峰值约为5kA，弧压约为200V；CB闭合瞬间，回路接通将焊锡丝熔断，间隙之间形成电弧，产生巨大声响并出现耀眼亮光，与爆炸过程类似；在电弧稳定燃烧阶段，电弧燃烧释放强烈的光和热，出现耀眼的白色弧光，如图2（a）所示；随着燃弧的进行，间隙亮度明显降低，如图2（b）所示，这时燃弧过程已接近尾声，间隙出现了大量线条形炽热颗粒，并向四周喷射，这主要由于电弧弧根温度较高，造成与其接触的金属电极熔化，而产生大量金属液滴所致；当电流过零熄弧时，弧光消失，但间隙仍出现了大量炽热的金属颗粒与明亮的火光，并产生了较多白烟，如图2（c）所示，说明铜电极发生了熔化、蒸发，并与周围空气发生了剧烈的化学反应，释放大量热量；随着电弧的熄灭，铜电极表面的温度逐渐降低，金属液滴的喷射现象逐渐减弱，火光与白烟也逐渐消散，如图2（d）～（f）所示。

2.2 基于CFD法的间接耦合分析方法

由上述短路燃弧现象，以及前期研究［13－19］表明，开关设备内部发生短路燃弧故障时，主要会经历以下4个阶段：压缩、膨胀、喷射以及热效应阶段，各阶段对应的压强变化如图3所示。由图可知，设备内部发生短路燃弧故障时，压力及热效应的影响时间段并不相同；燃弧5～15ms期间，设备内部压力急剧增大，而内部仅电弧区域附近的温度较高，开关设备泄压装置开启后，内部压力迅速下降至大气压，此时温度的影响才逐渐凸显；即热效应仅在燃弧末期影响较大，而对开关设备来说压力形成的破坏力对壳体以及建筑物的影响极大。因此，为了简化计算，同时获得较为准确的压力分布，提出了图4所示基于CFD法的间接解耦方法；该方法将电弧等离子体等效为理想气体，忽略了电弧本身的物理特性，同时不考虑电弧在磁场、流体场中的运动特性，仅将电弧当作热源，采用有限体积法进行温度－流体场耦合求解；由于该方法忽略了电磁场与温度－流体场的相互耦合作用，可大大减少计算量，并可对设备内部的压力升实现局部化求解。其中，加载热源功率P可根据：

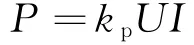
获得。式中：U为电弧弧压，I为电弧电流。

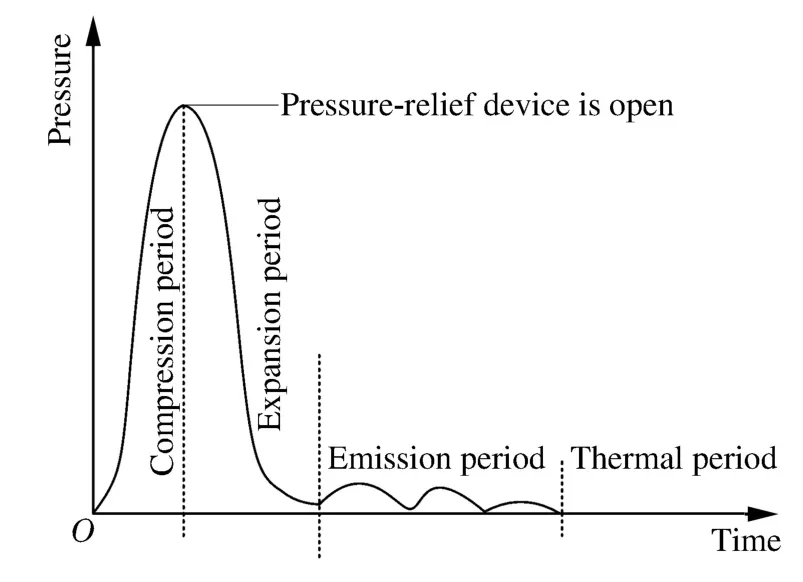
图3 燃弧过程的各个阶段Fig.3Phases of the arcing process

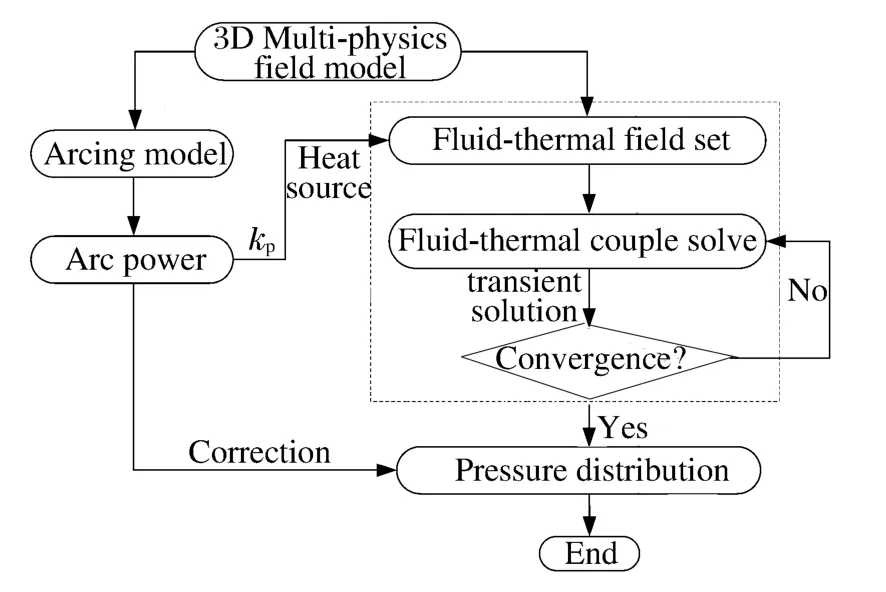
图4 压力升间接耦合算法Fig.4Indirect coupling analysis method of pressure rise

2.3 计算方法验证

为了验证数值模拟算法的准确性，建立了如图5所示的模型，容器直径0.7m、高0.8m，电极为圆柱形铜电极，其直径为2cm，位于容器正中央，电极间距为5cm；利用图1所示L－C振荡回路提供短路电流，实验方法与2.1部分一致，实验过程对电弧电流、弧压以及容器内表面的压力进行测量，压力监测点位于容器侧壁dp所示位置。通过电弧功率及燃弧时间可获得电弧释放的总能量约为8.246kJ，采用CFD法计算和实验测量获得监测点的压强随时间的变化规律如图6所示。

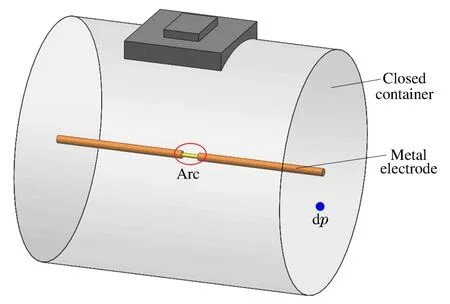
图5 实验模型Fig.5Experimental model

由图6可知，数值模拟获得的压强随时间的变化趋势与实验测量完全一致，但实验获得的压强曲线波动较大，基本以计算波形为中心上下振荡，这主要与实验过程电弧的剧烈变化有关。电弧燃烧过程中，由于弧压的波动，使得电弧功率的波动较大，并非为规则的正弦波，而数值计算中，假设电弧功率随时间呈正弦函数规律变化。因此，计算获得的压强曲线整体波动较小，波动频率与电弧功率一致；当燃弧至60ms时，计算与实验获得的相对压强最大值分别为：5.636和6.339kPa，两者相差达到了12.5%，但实验测量的平均压强为5.75kPa，两者仅相差2%左右；考虑到实验测量过程中电弧能量的波动，结果应参考平均压强的大小。因此，模拟结果与实验结果基本一致，证明了计算的有效性。

图6 实验结果与计算结果对比Fig.6Comparison of calculated and experimental results

3 封闭容器内部短路燃弧压力升数值模拟分析

3.1 电弧尺寸对压力升计算的影响

实际开关设备发生内部短路燃弧故障时，电弧在磁场力、热浮力以及气流等的影响下，燃弧位置、长度均会发生较大变化，因此，数值计算中电弧尺寸的选择成为重点问题。该部分就电弧尺寸对模拟结果的影响进行分析，建立了如图5所示的圆柱形封闭容器数值模型，同时为简化分析，容器直径与长度均减小为0.3m；燃弧部位（能量输入部位）为图中电弧区域，该区域的大小与电弧电流以及电弧的运动形态有关，燃弧间距设为5cm。由于燃弧时间较短，壁面与空气热交换的能量较少，因此，模拟过程将电极与容器壁面均设为绝热边界，容器内部气体为理想可压缩气体，初始温度为25℃，相对压强为0。假设电弧为圆柱形，直径分别设置为1和2cm；加载的热源功率为：

式中：t为燃弧时间，s。

利用图4所示方法计算获得热源直径为1和2cm的截面压强分布如图7所示。图中分别为时刻0.4和10ms的结果，可以看出，压强在截面基本呈现对称分布，说明压力波以电弧为中心向四周对称发展，能量的释放过程与爆炸过程类似，气体热浮力的影响较小；两种电弧直径获得的压强分布较为接近，如燃弧至10ms时，其对应的压强最大值分别为94.3和94.6kPa，两者仅相差0.3%左右，同时压力波由电弧区域传递至壁面的时间均约为0.4ms，说明压力波的传播速度也基本一致，约为375m／s；虽然图中最大值出现的位置有所不同，但其数值并无较大差异；可见当热源在容器内部占的空间较小时，其尺寸大小对压力的分布及传播特性影响较小；而实际开关设备发生内部短路燃弧故障时，电弧占的区域均较小，因此，电弧尺寸对计算结果的影响较小。

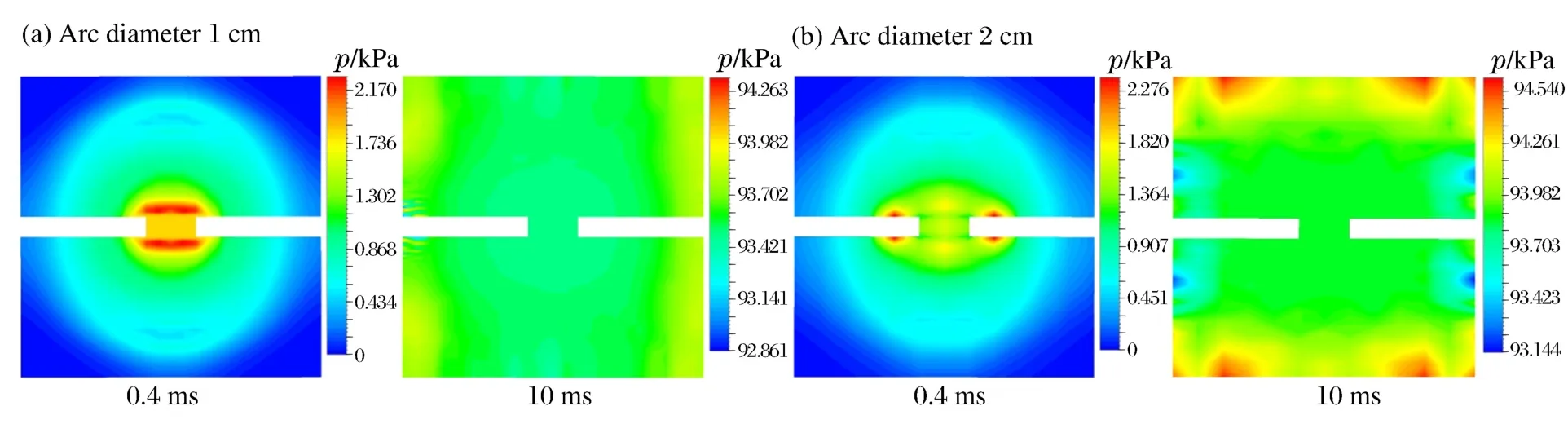
图7 不同电弧尺寸下压强分布Fig.7Pressure distribution in different arc sizes

3.2 电弧能量的影响

为分析电弧能量对容器内部压力升的影响，对上述模型在不同电弧能量下的压力升进行了计算，并考虑空气比热容随温度的变化，其变化规律可用文献［20］中的多项式进行描述；电弧能量Q分别为：9、18、36和56.7kJ。图8所示为计算获得的容器内部平均压强随电弧能量的变化规律。由图8可知，压强随电弧能量的增加近似线性增大，但增大速率并非为固定值，而是有减缓的趋势；压强增长率的平均值约为9.33kPa／kJ，当Q由9kJ增大到18kJ时，压强的增长速率约为9.98kPa／kJ；而当Q 由36kJ增大到56.7kJ时，压强增长率低于初始增长率；分析认为，随着电弧能量的增加，容器内部空气温度增大，导致空气比热容的波动较大；而当温度低于3 000K时，空气比热容随温度的增加而增大；在上述电弧能量的作用下，空气的平均温度均低于3 000K，所以随着电弧能量的增加，空气的比热容也会有所增大，而压强与空气比热容呈负相关，从而使得压强的增长速率减缓。由于空气比热容随温度和压强的变化较为复杂，对于更大电弧能量下压强的变化规律还需开展进一步的分析。

3.3 负压室的影响

由式（3）可知，容器内部的压强随容积的增大而减小，因此，为抑制开关设备内部的压力升，提出了图9所示的泄压通道优化措施。在燃弧室外部安装负压室，负压室与外部环境相连，当燃弧室的压力达到泄压盖A的阈值开启压力时，泄压盖A开启，燃弧室中部分高温气体瞬间被吸入负压室，此时负压室内压力升高出现超压。当其压力达到泄压盖B的开启压力时，内部气体被排至外界环境中，燃弧室中的压力将快速下降，可有效降低燃弧室出现爆裂的风险。假设燃弧室为边长50cm的正方体，负压室尺寸为20cm×20cm×40cm，初始相对压强为－10kPa，泄压盖A和B的阈值开启相对压强分别为10和0kPa。采用上述方法计算燃弧室的压力分布发现：增加负压室后，燃弧室中的最大压强降低了约60%，可见负压室的降压效果较好，可应用于实际开关设备中，但具体应用方案有待进一步深入研究。

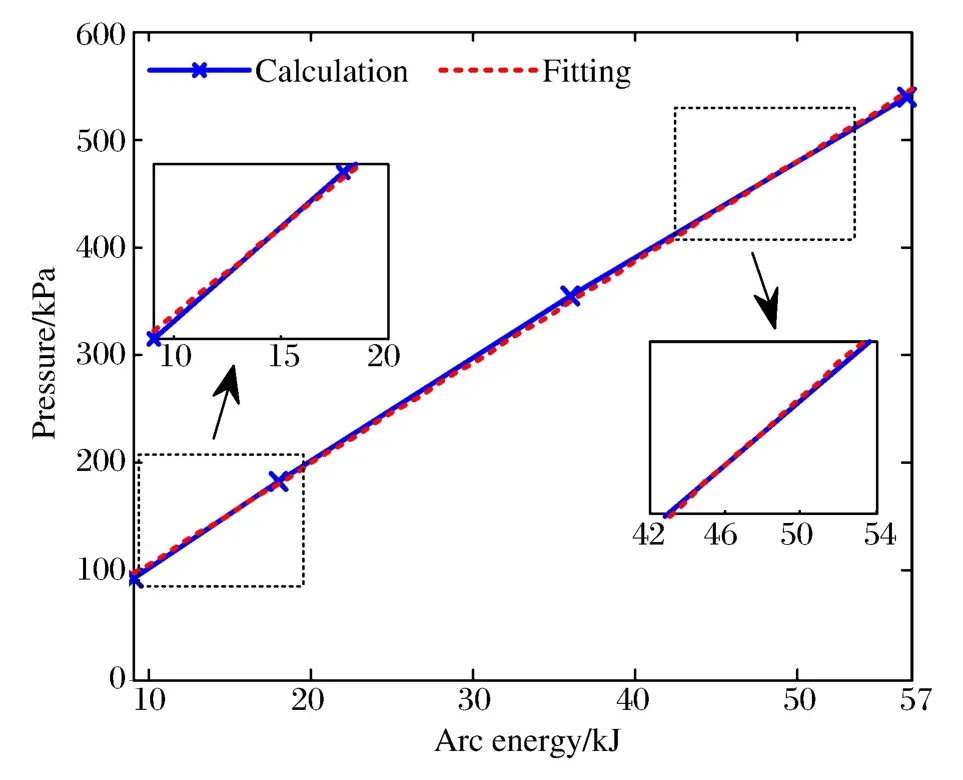
图8 压强随电弧能量的变化Fig.8Variation of pressure with arc energy

图9 泄压通道优化措施Fig.9Optimization measure of pressure relief channel

4 结 论

分析了容器内部短路燃弧引起的热－力效应，提出了基于CFD法的压力升间接耦合分析方法，通过小尺寸模型的实验与仿真分析，对该方法的可行性和有效性进行了验证，并分析了相关规律，得到了如下结论：

（1）基于CFD数值计算与实际实验获得的压力升仅相差2%左右，验证了该计算方法的有效性，但如何获得较为准确的温度分布以及在实际开关设备中的应用将在后续开展进一步研究；

（2）电弧尺寸对开关设备内部压力升分布规律的影响较小；容器内部压力升随电弧能量的增加近似线性增大，随容器体积的增大而快速减小；

（3）在燃弧室外部加装负压室可有效降低容器内部的压力升，因此对于实际开关设备，可通过增设负压室来减弱短路爆炸产生的冲击波对设备的影响。

［1］ Daalder J E，Lillevik O，Rein A，et al.Arc in SF6－MV－Switchgear pressure rise in equipment room［C］∥14th International Conference and Exhibition on Electricity Distribution，Brighton，UK，1989：37－41.

［2］ 熊泰昌.高压开关柜防护内部电弧故障的结构强度计算与试验研究［J］.上海电器技术，2002（3）：124－128.Xiong Taichang.Strength calculation and test research of high－voltage switchgear against internal arc faults［J］.Shanghai Electric Application Technolgy，2002（3）：124－128.

［3］ 蓝会立，张认成.开关柜内部故障电弧探测法的研究现状及趋势［J］.高电压技术，2008，34（4）：496－499.Lan Huili，Zhang Rencheng.Current research and development trends on faults arc detection method in switch cabinet［J］.High Voltage Engineering，2008，34（4）：496－499.

［4］ 王伟.12kV开关柜内部燃弧仿真及柜体强度优化［D］.沈阳：沈阳工业大学，2012.

［5］ 熊泰昌.内部电弧故障试验情况下中压开关柜强度计算［J］.高压电器，2002，38（4）：42－44.

Xiong Taichang.Strength calculation of medium voltage switchgear under internal arc－fault test［J］.High Voltage Apparatus，2002，38（4）：42－44.

［6］ Friberg G，Pietsch G J.Calculation of pressure rise due to arcing faults［J］.IEEE Transactions on Power Delivery，1999，14（2）：365－370.

［7］ Lutz F，Pietsch G.The calculation of overpressure in metal－enclosed switchgear due to internal arcing［J］.IEEE Transactions on Power Apparatus and System，1982，PAS－101（11）：4230－4236.

［8］ Dasbach A，Pietsch G J.Calculation of pressure waves in substation buildings due to arcing faults［J］.IEEE Transactions on Power Delivery，1990，5：1760－65.

［9］ Uzelac N，Dullni E，Kriegel M，et al.Application of simplified model for the calculation of the pressure rise in MV switchgear due to internal arc fault［C］∥22nd International Conference on Electricity Distribution.Stockholm，Sweden，2013：10－13.

［10］ Iwata M，Anantavanich K，Pietsch G.Influence of arc current on fraction kpof electric arc energy leading to pressure rise in a closed container［C］∥17th International Conference on Gas Discharges and their Application.Cardiff，UK，2008：189－192.

［11］ Iwata M，Anantavanich K，Pietsch G.Influence of current and electrode material on fraction kpof electric arc energy leading to pressure rise in a closed container during internal arcing［J］.IEEE Transactions on Power Delivery，2010，25（3）：2028－2029.

［12］ Zhang X，Pietsch G，Gockenbach E.Investigation of the thermal transfer coefficient by the energy balance of fault arcs in electrical installations［J］.IEEE Transactions on Power Delivery，2006，21（1）：425－431.

［13］ 黄锐，胡毅亭，马炳烈，等.开关柜内部电弧故障产生力和热的计算模型［J］.爆炸与冲击，2000，20（2）：125－130.

Huang Rui，Hu Yiting，Ma Binglie，et al.Calculation model for the effects of force and heat produced by inner arc fault in switchgear cabinet［J］.Explosion and Shock Waves，2000，20（2）：125－130.

［14］ 蔡彬，陈德桂.中压开关柜中内部电弧故障的计算方法和防护措施［J］.高压电器，2003，39（1）：8－11.

Cai Bin，Chen Degui.The calculation and protection measures of internal arcing faults in MV metal－clad swtichgear［J］.High Voltage Apparatus，2003，39（1）：8－11.

［15］ Cai bin，Chen Degui，Li Zhipeng.Simulation and experiments on internal arcing faults in MV metal－clad switchgear［J］.Transactions of China Electrotechnical Society，2004，3（3）：82－87.

［16］ Rong Mingzhe，Li Mei，Wu Yi，et al.3－D MHD modeling of internal fault arc in a closed container［J］.IEEE Transactions on Power Delivery，2017，32（3）：1220－1227.

［17］ Wu Yi，Rong Mingzhe，Yang Fei，et al.Experimental and theoretical study of internal fault arc in a closed container［J］.Journal of Physics D：Applied Physics，2014，12（11）：1873－1886.

［18］ Zhang X，Zhang J，Gockenbach P.Calculation of pressure and temperature in medium－voltage electrical installations due to fault arcs［J］.Journal of Physics D：Applied Physics，2008，41（10）：1－11.

［19］ Wactor M，Olsen T W，Ball C J，et al.Strategies for mitigation the effects of internal arcing faults in mediumvoltage metal－enclosed switchgear［J］.Transmission ＆ Distribution Conference ＆ Exposition，2001，9（1）：323－328.

［20］ 梁德旺，李博，容伟.热完全气体的热力学特性及其 N－S方程的求解［J］.南京航空航天大学学报，2003，35（4）：424－429.Liang Dewang，Li Bo，Rong Wei.Thermodynamic characteristics of thermally perfect gas and solution of N－S equations［J］.Journal of Nanjing University of Aeronautics ＆ Astronautics，2003，35（4）：424－429.

Pressure effect calculation of internal short－circuit arcing explosion in a closed container

Li Peng1，Ruan Jiangjun1，Huang Daochun1，Xu Guoshun2，Long Mingyang1，Wei Mengting1
（1.School of Electrical Engineering，Wuhan University，Wuhan 430072，Hubei，China；2.School of Electrical Engineering，Naval University of Engineering，Wuhan 430033，Hubei，China）

Internal short－circuit arcing explosion in a medium－voltage（MV）switchgear poses a serious hazard to the safety of equipments，buildings and personnel.In the present work，to find out an appropriate method to calculate the pressure effect resulting from the internal arcing explosion，we analyzed the energy balance mechanism of the internal arcing in the switchgear，presented an indirect coupling analysis method based on CFD through the analysis of the thermal－mechanical effect of the arcing process，and verified the method by the actual arcing in a closed container.The results show that the relative error of the average pressure rise between measurement and calculation is about 2%.The arc size has less effect on the pressure rise.In the closed container，the pressure rise approximately increases linearly with the increase of the arc energy.The installation of a negative pressure room can reduce the pressure in the arcing room 60%，thereby effectively restraining the pressure rise in the switchgear caused by the internal short－circuit arcing explosion.

switchgear；internal short－circuit arcing；closed container；CFD；pressure rise

O389 国标学科代码：13035

A

10.11883／1001－1455（2017）06－1065－07

2016－04－12；

2016－10－19

国家科技支撑计划项目（2009BAA19B05）；中央高校基本科研业务费专项基金项目（2042016gf0008）

黎 鹏（1989— ），男，博士研究生，lipeng19891102＠126.com。

（责任编辑 曾月蓉）