基于混合GEP的配电低压台区综合评价算法*

王栋，蒋亮，江陈桢，李珺涵，胡斌，朱力鹏，邓松

（1.国网南通供电公司，江苏南通226001；2.全球能源互联网研究院，北京102209；3.南京邮电大学，南京210023）

0 引 言

配电网处于电力系统的末端，具有地域分布广、电网规模大、设备种类多、网络连接多样、运行方式多变等鲜明特点［1－2］。

随着智能电网的不断发展，用户的用电量和对电能质量的要求不断提高，有些地方的低压配电网电能质量和供电能力无法满足广大用户的要求。低压配电网具有规模巨大、结构复杂、不确定的信息较多、智能化不够等特征，正是这些特征对智能配电低压台区的综合评价带来一定的挑战。影响智能配电网低压台区综合评价的指标特征很多，各指标之间的发展程度也各不相同。整个智能配电网低压台区综合评价是综合低压配电网建设的重要依据，这为配电网进一步科学的规划、建设和管理提供决策。

针对智能低压配电网的采集装置配置少、台区线路多样、管理复杂的现状，如何对众多配电低压台区进行一个综合评价，为后面的配电网低压台区规划建设提供决策依据是亟待解决的一个难题。文献［3］提出了一种面向台区管理的台区状态综合评价方法，设计了低压配电网台区的特征指标体系，构建了低压配电网台区状态综合评价模型，最后实际台区数据验证了该模型的正确性和适用性。张梦等提出了基于智能化的农村低压配电网台区管理方法和相应的措施，以满足低压配电网负荷增长的实际需求，提高低压配电网的供电可靠性和电能质量［4］。文献［5］针对城市配电网规划缺乏有效的量化手段的情况，提出一种有关配电网规划的综合评价指标体系与方法。现有的这些配电网综合评估方法存在主观性强、评价指标体系复杂多样等问题，为了更好地解决智能低压配电台区的高效准确评估，本文结合粗糙集和基因表达式编程的思想，提出一种基于混合基因表达式编程的智能配电网低压台区综合评价算法（Comprehensive evaluation algorithm of low voltage station area in smart distribution network based on hybrid gene expression programming，CE-LVHGEP）。

文章所做的主要工作如下：（1）为了解决影响智能配电网低压台区综合评价因素过多的问题，本文提出基于粗糙集的智能配电网低压台区综合评价指标约简算法（Attribution reduction algorithm of comprehensive evaluation index in low voltage smart distribution network based on rough set，AR-CEILV）；（2）在AR-CEILV基础上，结合基因表达式编程的思想，提出基于混合基因表达式编程的智能配电低压台区综合评价算法（CE－LVHGEP）。

1 基于粗糙集的智能配电网低压台区综合评价指标约简算法

1.1 问题描述

为了更好地对智能配电网低压台区进行综合评价，首先要做的就是梳理影响智能配电网低压台区综合评价的各类要素。文献［6］指出影响智能配电网低压台区综合评价的主要指标包括电网投资、运维管理、客户服务和外部因素等，其中电网投资又包括线路理论损耗率、线路统计损耗率、配变理论损耗合格率、容载比、平均供电半径以及户均容量等；运维管理又包括最小负荷率、峰谷差率、负荷率、功率因数、供电可靠性、配变最大负载率、三相不平衡率和电压合格率等；客户服务又包括到达时长和修复时长等；外部因素主要包括气温、湿度、台风和盐雾。

但由于影响配电网台区综合评价的要素复杂多样，则导致构成的配网台区综合评价要素集呈现出高维的特征，直接利用GEP进行评价函数的挖掘是一件非常困难的事。为了更好地对这些高维综合评价数据集进行有效的挖掘，首先要对这些高维要素集进行降维，而降维的方法很多，例如主成份分析方法［7］、奇异值分解法［8］及粗糙集［9］等。但前两种方法不可避免地会造成原始数据信息的部分丢失，而基于粗糙集的属性约简在降维的同时，并没有改变约简后数据的决策规则。为此，本文提出了基于粗糙集的智能配电网低压台区综合评价指标约简算法（AR-CEILV）。

1.2 相关定义

为了更好地描述问题，首先给出有关AR-CEILV算法中需要用到的相关定义。

定义1：综合评价决策表（Comprehensive Evaluation Decision Table，CE-DT）。

设 T＝＜U，C∪D，V，f＞，其中 U为配网台区综合评价要素集中的所有研究对象，C∪D＝R为配网台区综合评价要素集的属性集合，C＝{c1，c2，…，cn}为配网台区综合评价要素集中所有要素，D＝{d1，d2，…，dm}为配网台区综合评价要素集中的评价值集合，V＝∪vr，r∈Rs是配网台区综合评价要素集中各类指标值及对应的评价值的集合，vr表示某一个属性r∈R的范围，f∶U×R→V定义一个信息函数，它指定U中每一对象x的属性值，即对于∀r∈R，x∈U，有 f（x，r）∈vr。称满足上述条件的 T为综合评价决策表。

定义2：设综合评价决策 T＝＜U，C∪D，V，f＞，其中C∪D＝R，D的C正域是U中所有通过用U／C表达的集合能够确定地划入U／D类的对象的集合，记为 POSC（D）。

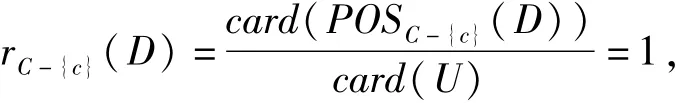
1.3 算法描述

整个基于粗糙集的智能配电网低压台区综合评价指标约简算法的描述如下所示：

算法1：AR-CEILV（T）

输入：T＝＜U，C∪D，V，f＞；

输出：T′＝＜U，C′∪D，V，f＞；

（1）C′＝C；

（2）针对配网台区综合评价要素集C中的每一个要素c；

（3）根据定义2和定义3分别计算POSC－{c}（D）和 rC－{c}（D）；

（4）若 rC－{c}（D）＝1，则说明要素 c是可约简的；

（5）返回约简后的 T′。

整个算法的计算耗时集中在rC－{c}（D）的计算上，因此整个算法的时间复杂度大约为 O（Card（C））。

2 基于混合基因表达式编程的智能配电网低压台区综合评价算法

2.1 问题描述

智能配电网低压台区综合评价可以看成是影响低压台区综合评价的指标与评价值之间的函数挖掘。通过基于粗糙集的智能配电网低压台区综合评价指标约简，可以对高维台区综合评价数据集进行有效地降维，由于粗糙集本身的特性，这种降维处理并没有改变原来数据集固有的决策属性和能力。因此在粗糙集属性约简的基础上，再基于基因表达式编程进行智能配电网低压台区综合评价函数挖掘和直接利用基因表达式编程进行台区综合评价函数挖掘的效果是一致的。

在实际应用中，挖掘数据之间蕴含的函数关系，有助于揭示数据的内在本质。传统的回归方法一般都假定了函数类型已知，然后借助最小二乘法［10］或者其改进的方法进行参数估计，最后确定函数关系式。这些方法过于依赖先验知识，含有很多主观人为因素，目前还不能解决复杂函数关系式的建立，而且对于复杂高维的样本数据，计算量较大，算法复杂度较高，计算效率低下。为此，在文献［11-12］中，作者使用遗传编程（GP）来进行数学建模，得到了比较好的结果，同时还避免了传统统计方法事先选定函数模型的不足。但是利用GP来挖掘函数模型的效率不高，文献［13-15］提出了一种新的算法－基因表达式编程（Gene Expression Programming，GEP），它和GP一样可以实现函数关系式的挖掘，在挖掘复杂函数关系式时，其效率高出传统的GA和GP算法4-6个数量级。本文在AR-CEILV算法的基础上，结合基因表达式编程算法的优势，提出一种基于混合GEP的智能配电网低压台区综合评价算法（CE-LVHGEP）。

2.2 算法描述

整个基于混合GEP的智能配电网低压台区综合评价算法的形式化描述如下。

算法2：CE-LVHGEP

输入：综合评价决策表T，种群大小PopSize，最大迭代次数MaxGen；迭代终止的适应值MaxFitness，选择率 Ps，变异率 Pm，插串率 Pt，重组率 Pr；

输出：最优的综合评价函数BestEFun.

（1）T′←AR－CEOLV（T）；

（2）根据约简后的综合评价决策表 T′初始化种群；

（3）While（fitness＜＝MaxFitness）or（genNum＜＝MaxGen）do；

（4）按照选择概率Ps、变异概率Pm、插串概率Pt、重组概率Pr分别执行选择、变异、插串及重组操作，并形成新的种群；

（5）评价新的种群；

（6）返回最优的综合评价函数BestEFun。

3 仿真实验与分析

3.1 仿真实验环境和数据来源

为了更好地验证本文所提出算法的可行性和有效性，在实验室环境下做了大量的仿真实验。整个实验平台为 Win7 Professional＋Eclipse 3.2＋Java1.7，所有的程序由Java语言实现。

本实验的数据主要来源于国网南通市供电公司。首先分析影响南通市供电公司配电网低压台区评价的指标要素，得到相应的综合评价要素集，并通过该综合评价要素集中所有的值构造相应的综合评价决策表。整个决策表中条件属性（也即综合评价指标要素）个数为20，决策属性（也即综合评价等级）个数为5（分别为较高、高、中、低、较低），数据个数为200条，其中其150条数据为训练数据，后50条数据为测试数据。

3.2 实验分析

实验1：针对上述已知的智能配电网低压台区综合评价决策表，表1给出综合评价决策表基于ARCEILV算法进行指标约简前后影响智能配电网低压台区综合评价的指标个数变化。表2给出了AR-CEILV、PCA、SVD以及基于正域的属性约简算法（（Attribute Reduction Algorithm based on Positive Region，ARPR））和基于分辨矩阵的属性约简算法（Attribute Reduction Algorithm based on Discernable Matrix，ARDM）求解出的最优属性约简。图1显示了在算法运行5次的情形下，FAR-BSA算法与 PCA、SVD、AR-PR、AR-DM求解一个最优属性约简的耗时比较。

表1 基于AR-CEILV的综合评价指标的个数变化Tab.1 Change of the number of comprehensive evolution index based on AR-CEILV

我们知道，对于固定综合评价指标个数而言，最优指标约简不唯一，从表1中可以看出，AR-CEILV在求解一个最优属性约简是有效的。约简后的综合评价指标个数减少了70%，从而大大降低了后续综合评价函数挖掘的复杂度。同时根据粗糙集理论，属性约简并没有改变智能配电网低压台区综合评价分析决策能力。

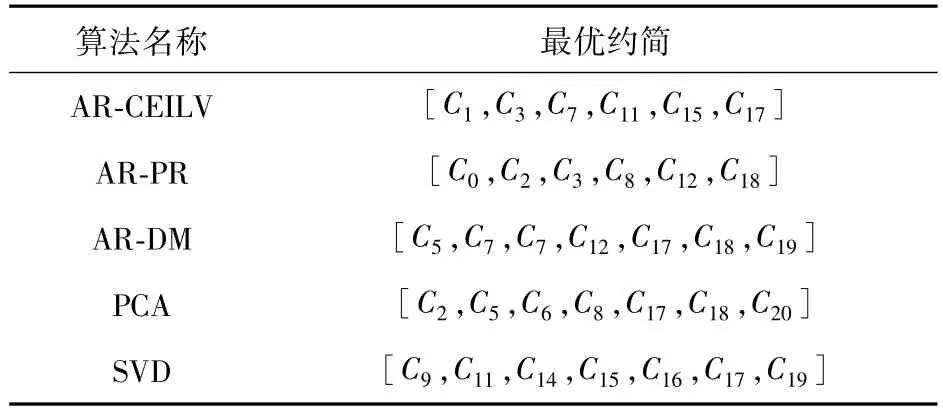
表2 各类约简算法求解一个最优约简比较Tab.2 Comparison of the optimal reduction of five algorithms

从表2中可以看出，AR-CEILV、AR-PR和 ARDM三种算法求解出的一个最优约简中都包含6个条件属性。PCA求解出的最优约简中包含7个条件属性，SVD求解出的最优约简中包含8个条件属性。其中AR-CEILV、AR-PR和AR-DM三种算法是基于粗糙集实现，求解出的最优约简并不会造成原有智能配电网低压台区综合评价决策表的信息损失，而PCA是基于统计分析，SVD是基于矩阵分解来进行约简，不可避免都会造成原有信息的部分损失。

图1 五种算法求解一个最优约简的耗时比较Fig.1 Consuming time comparison of optimal reduction of five algorithms

实验2：在实验1的基础上，针对约简后形成的智能配电网低压台区综合评价决策表，本实验阐述了CE-LVHGEP的性能。整个实验中GEP的参数如表3所示。图2给出了GEP算法对约简前后的智能配电网低压台区综合评价决策表进行评价函数挖掘时的最优适应度与最大适应度值差值的比较。图3显示了在重复5次实验，每次实验算法运行10次的条件下，约简前后GEP函数挖掘的平均耗时比较。图4显示了基于CE-LVHGEP挖掘得到的综合评价函数模型对测试数据的模型值与真实值之间的比较。

表3 GEP参数Tab.3 GEP parameters

基于表3所示的GEP参数，挖掘得到最终的最优配电网低压台区综合评价函数模型：

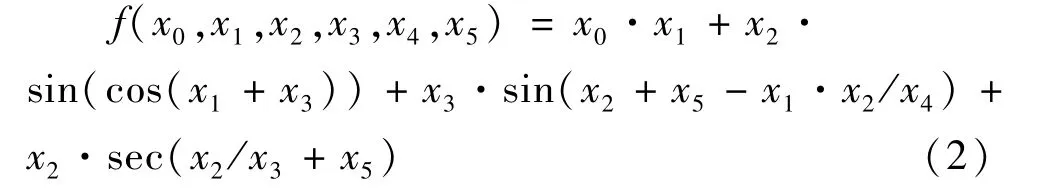
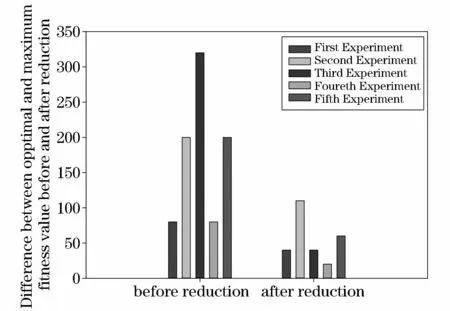
图2 约简前后GEP算法的最优适应度值与最大适应度值差值比较Fig.2 Comparison of difference between optimal and maximum fitness value before and after reduction

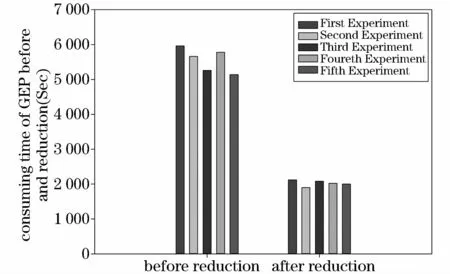
图3 约简前后GEP算法的平均耗时Fig.3 Average consuming time of GEP before and after reduction

从图2中可以看出，针对本文所提供的实验样本数据集而言，约简后比约简前GEP算法进行智能配电网低压台区综合评价函数挖掘所得到的最优适应度值与最大适应度值差值最大下降了约87.5%，根据定义6得到函数挖掘成功率最大达到约99.73%。这表明针对高维数据集，在不改变现有数据集决策分析能力的前提下，属性约简大大提高GEP函数挖掘的成功率。与此同时，图3显示，针对相同的智能配电网低压台区综合评价决策表，约简大大降低了GEP综合评价函数挖掘的平均耗时，5次相同参数的实验中平均耗时最大下降约66.43%。

图4 综合评价决策表中测试数据真实值与模型值比较曲线图Fig.4 Comparison curves between the values of test data and model values in comprehensive evolution table

图4反映了智能配电网低压台区综合评价决策表中测试数据真实值与模型值之间的拟合程度。从图4中可以看出，有关综合评价测试数据基于式（2）计算得到的模型值与真实值之间最大的误差为0.3，最小为0.01，R2的值为0.954。由此可以看出该模型具有较高的预测精度。

针对智能配电网低压台区综合评价来说，基于CE-LVHGEP的综合评价函数模型预测精度越高，对未来基于该模型进行智能配电网低压台区运行状态的综合评估和预测起到至关重要的作用。

4 结束语

随着配电自动化、用电信息采集等应用系统的推广应用，智能配电网低压台区的综合评价对于整个配电网台区的规划、建设及运行具有重要的指导意义。本文提出基于混合基因表达式编程的智能配电网低压台区综合评价算法（CE-LVHGEP）。在CELVHGEP算法中，为了对影响智能配电网低压台区综合评价指标要素复杂多样且数量众多的问题，提出了基于粗糙集的智能配电网低压台区综合评价指标约简算法（AR-CEILV）。仿真实验表明，CE-LVHGEP算法不仅可以快速挖掘出最优综合评价函数模型，同时得到的模型还具有较高的预测精度。这为未来智能配电网低压台区运行状态的综合评估和预测奠定了良好地算法基础。