高压输电线路故障测距综合优化方法研究

申元，姜志博，黄修乾，宋文波，王科，黑颖顿

（1.云南电网有限责任公司电力科学研究院，昆明 650000；2.国网电力科学研究院武汉南瑞有限责任公司，武汉 430074；3.云南电网有限责任公司，昆明 650000）

0 引 言

随着我国电力工业的飞速发展，高压、超高压长输电线路的日益增多，实现对长距离输电线路故障的精准定位对于提高系统供电可靠性，保证电网安全稳定运行能力具有重要意义［1］。

目前的故障测距方法按原理可分为两类：即行波测距法和故障分析法。文献［2］指出与传统的故障分析法相比，行波法具有受系统参数、过渡电阻、系统运行方式等其他因素较小的优点，但也存在诸如相应设备研制不成熟，波速确定精度和测距结果可靠性无法保证，以及多种波头检测方法之间的配合问题等。文献［3-4］指出在行波测距过程中，电流互感器是取得电流行波信号的耦合元件，其二次侧时间常数按试验数据估计约为数百微秒，同时还受铁芯饱和及剩磁影响，使得电流互感器的动态时延具有较大分散性，影响测距结果。故障分析法可进一步分为单端量法和双端量法。文献［5］指出单端量法无法从原理上同时克服过渡电阻和对端系统阻抗的影响。而文献［6］指出双端法又可分为基于双端同步采样数据的算法和无需双端同步的算法。前者需要两端电气数据同步，对硬件设备要求很高，后者精度受两端相角差影响较大，且存在伪根剔除问题。可以看到，现有故障测距算法均存在一定缺陷，同时其应用均具有一定局限性。

本文利用神经网络具有非线性处理和自适应学习的优点，提出了一种有效综合现有故障测距结果的输电线路故障测距方法。分别建立了以故障实际距离和故障测距误差为输出的两种综合模型，以仿真计算结果和实际故障测距结果作为训练样本对神经网络进行训练，并利用验证样本对所提出方法的正确性和有效性进行了验证，分析了两种综合模型的适用范围［7］。

1 BP神经网络

1.1 拓扑结构

BP神经网络是一种具有三层及以上的多层神经网络［8］，每一层都由若干个神经元组成，如图1所示，相邻层的各个神经元为全连接，而同一层神经元之间无连接。BP神经网络按照有导师学习方式进行训练，神经元激活值从输入层经各隐含层向输出层传播，然后按减小期望输出与实际输出之间误差的目标，从输出层经各隐含层，最后回到输入层逐层修正各连接权。由于这种修正过程是从输出到输入逐层进行的，故称之为“误差逆传播算法”［9］。

图1 BP网络模型结构Fig.1 BP network structure

1.2 神经网络训练

神经网络需要通过训练调整层间连接权值和节点阈值，使得在所有训练样本下的实际输出和期望输出之间的误差小于某个要求的水平［10］。通常BP网络的训练和学习包括如下步骤：

（1）初始化网络及学习参数，如网络初始权矩阵、学习因子等；

（2）提供训练模式训练网络，开始训练，如果此时误差小于给定值，则停止学习；

（3）前向传播过程：对给定训练模式输入，计算网络的输出模式，并与期望模式比较，若误差不符合停止条件，则执行步骤（4），否则返回步骤（2）；

（4）反向传播过程：计算同一层单元的误差，修正权值和阈值，返回步骤（2）。

网络的学习是通过给定的训练集训练而实现的。通常用网络的均方差误差来定量地反映学习的性能。一般地，当网络的均方差误差低于给定值时，则表明对给定训练集学习已满足要求［11］。

2 故障测距综合优化模型

2.1 第1种模型

第一种基于BP神经网络的故障测距综合模型如图2所示。

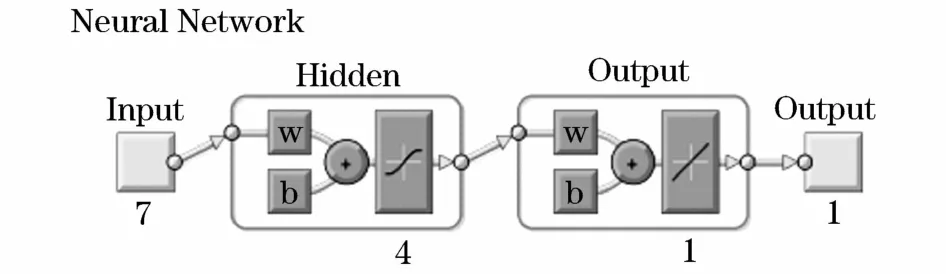
图2 第1种综合模型Fig.2 The first integration model

该BP网络采用七个输入，即过渡电阻值和6种测距方法所得到的故障距离，6种测距方法分别为双端算法1、解一次方程法、迭代法、解二次方程法、双端算法2、两端不同步算法，并分别以序号1～6表示。BP网络内部具有4个神经元，该综合模型的输出为实际故障距离，以序号7表示。

2.2 第2种模型

第二种基于BP神经网络的故障测距综合模型如图3所示。

图3 第2种综合模型Fig.3 The second integration model

与第一种模型不同之处在于第二种模型具有6个输出单元，输出结果分别为各种测距方案的测距误差。

3 基于仿真数据的故障测距融合

3.1 第2种模型

基于PSCAD搭建输电线路故障仿真模型如图4所示，将所得到的故障数据导入至MATLAB，根据6种测距方案原理编写测距算法，得到各个测距算法的测距结果，再将各测距结果作为训练样本输入至神经网络进行训练，训练完成的神经网络模型即可进行后续故障测距综合优化评估。

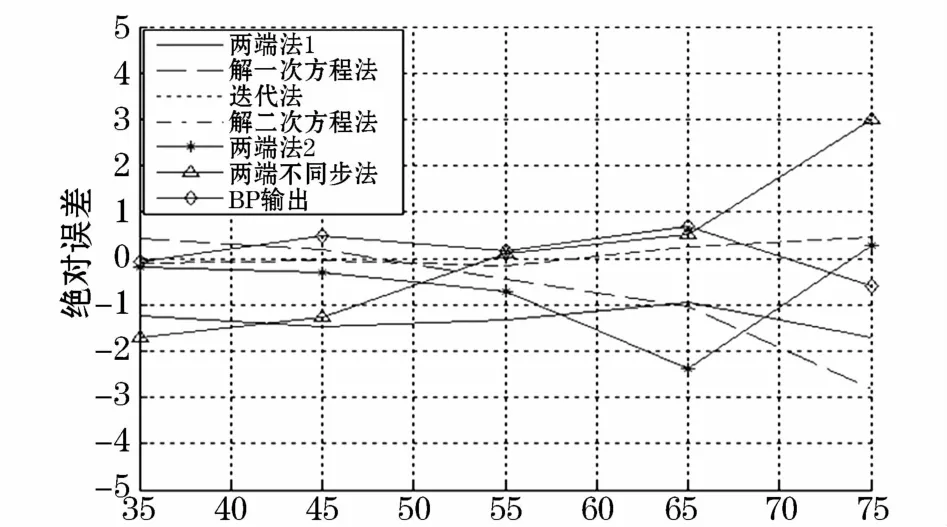
图4 测距结果比较（km）Fig.4 Comparison of the distance measurement results（km）

输电线路设置为100 km，分别设置过渡电阻为10Ω、50Ω和100Ω，以10 km为间隔，设置故障发生距离线路首端10 km～90 km处，过渡电阻50Ω时的训练样本如表1所示，限于篇幅，其他两种过渡电阻时的数据未给出。

表1 过渡电阻50Ω时的训练样本（km）Tab.1 Training samples with 50Ω transition resistance（km）

设置过渡电阻50Ω，分别设置故障距离为35 km，45 km，55 km，65 km和75 km，以所得到的故障测距结果作为验证样本，故障测距综合模型1输出结果如表2所示。

表2 综合模型1输出结果（km）Tab.2 Output result of integration model 1（km）

图4给出了各测距算法及综合模型1在验证样本下测距绝对误差。

同理，设置过渡电阻100Ω，故障距离分别为35 km，45 km，55 km，65 km和75 km，各测距算法及综合模型1的测距绝对误差变化如图5所示。

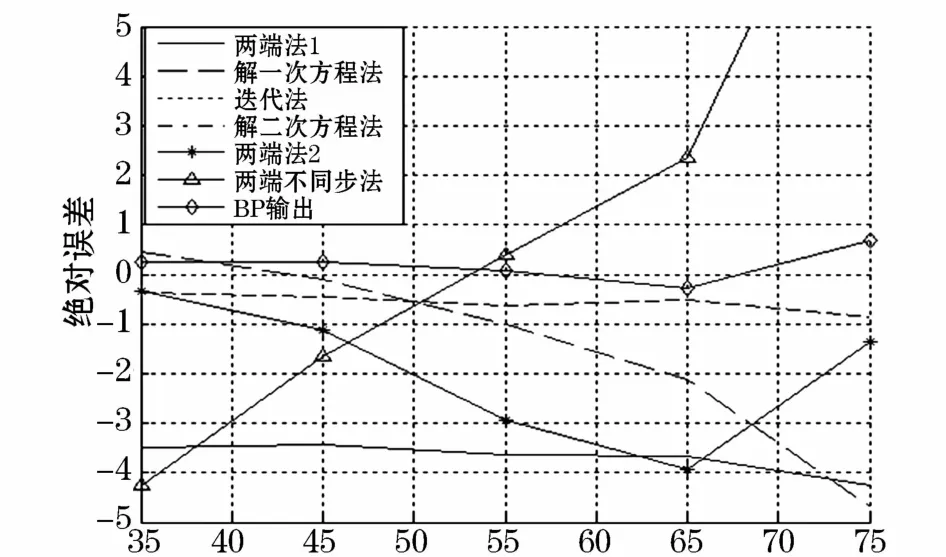
图5 测距结果比较（km）Fig.5 Comparison of the distance measurement result（km）

由图4和图5可知，无论过渡电阻为多大，综合模型1所得到的故障距离绝对误差比其他6种测距结果的都要小，表明所提出的综合算法能够充分融合现有各故障测距算法的结果，提高故障测距的精度。同时对比两图可知，当过渡电阻增大时，现有各测距算法的绝对误差将变大，但综合模型1的测距结果基本不受过渡电阻的影响，仍具有最高的精度。

3.2 第2种模型

第2种综合模型输出6种测距算法的相对测距误差，训练样本通过将表1所示的绝对距离改为相对误差得到，如表3所示。

在过渡电阻50Ω，故障距离分别为35 km，45 km，55 km，65 km和75 km时，各测距算法和综合模型2所得结果见表4。各测距算法测距结果如图6所示。

表3 过渡电阻50Ω时的训练样本（%）Tab.3 Training samples with 50Ω transition resistance（%）

表4 综合模型2输出结果（%）Tab.4 Output result of integration model 2（%）

图6 测距结果比较（%）Fig.6 Comparison of the distance measurement result（%）

由上述结果可知，故障距离不同时，各个测距算法具有不同的精度，例如故障距离35 km时，迭代法具有最高的精度，测距结果为34.89 km。综合模型2能够确定出每次故障测距中具有最高精度的结果。

3.3 综合模型的适用性分析

综合模型1输出为某次故障的绝对距离，适用于各测距方法输出结果相差不大的情况。综合模型2给出6种测距算法可能的相对误差，可选取相对误差最小的一个作为最终测距结果。该模型适用于实际应用中，可能出现的由于设备精度和其他原因导致的测距失败，测距结果相对差别较大，甚至出现超出线路全长的情况。

4 实际算例分析

4.1 综合模型1

本文应用云南地区220 kV雷击故障实际测距结果来说明两种综合模型的应用，实际情况下需要将测距失败的数据剔除，比如测距结果超出线路全长。部分故障数据如表5所示。

以表9中前13行数据作为训练样本，以最后一组数据作为验证样本。综合模型1输出的本侧测距结果为0.795 5（以线路总长为基准值的标幺值），故障距离51 320.09 m，而实际故障距离为0.80，故障距离51 644 m。可以看到，综合模型1相对其他测距算法具有最高的故障测距精度，表明该模型具有较好的实用性。

4.2 综合模型2

以本侧测距结果和对侧测距结果分别建立两个综合模型2的神经网络，以前13行数据作为训练样本，以最后一组数据作为验证样本。

本侧测距模型输出误差为［-0.01%，-0.03%，-0.05%］，表明第一种测距算法，即主一保护测距（本侧）具有最高精度，测距结果为52 340 m，而实际故障距离51 644m。

对侧测距模型输出误差为［-0.44%，16.40%，5.43%］，表明第一种测距算法，即主一保护测距（对侧）具有最高精度，测距结果为13 051 m，而实际故障距离12 869 m。

4.3 结果分析

由表5可以看到，本侧测距结果精度都较高，因此可采用综合模型1，结果表明其测量距离与实际距离相差不超过350 m。而由于对侧测距结果相差较大，故障录波测距多次测得超出线路全长的结果，因此采用综合模型2比较合适。结果表明，应用该模型得到故障距离误差只有182 m，满足测距精度要求。

但故障测距领域，一直存在“可测不可量”的问题，即由于导线弧垂、环境温度等外界条件影响，计算出的结果和实际值相差较大。可采用文献［12］提出的方法，利用故障距离与线路全长的比值来提高测距精度。

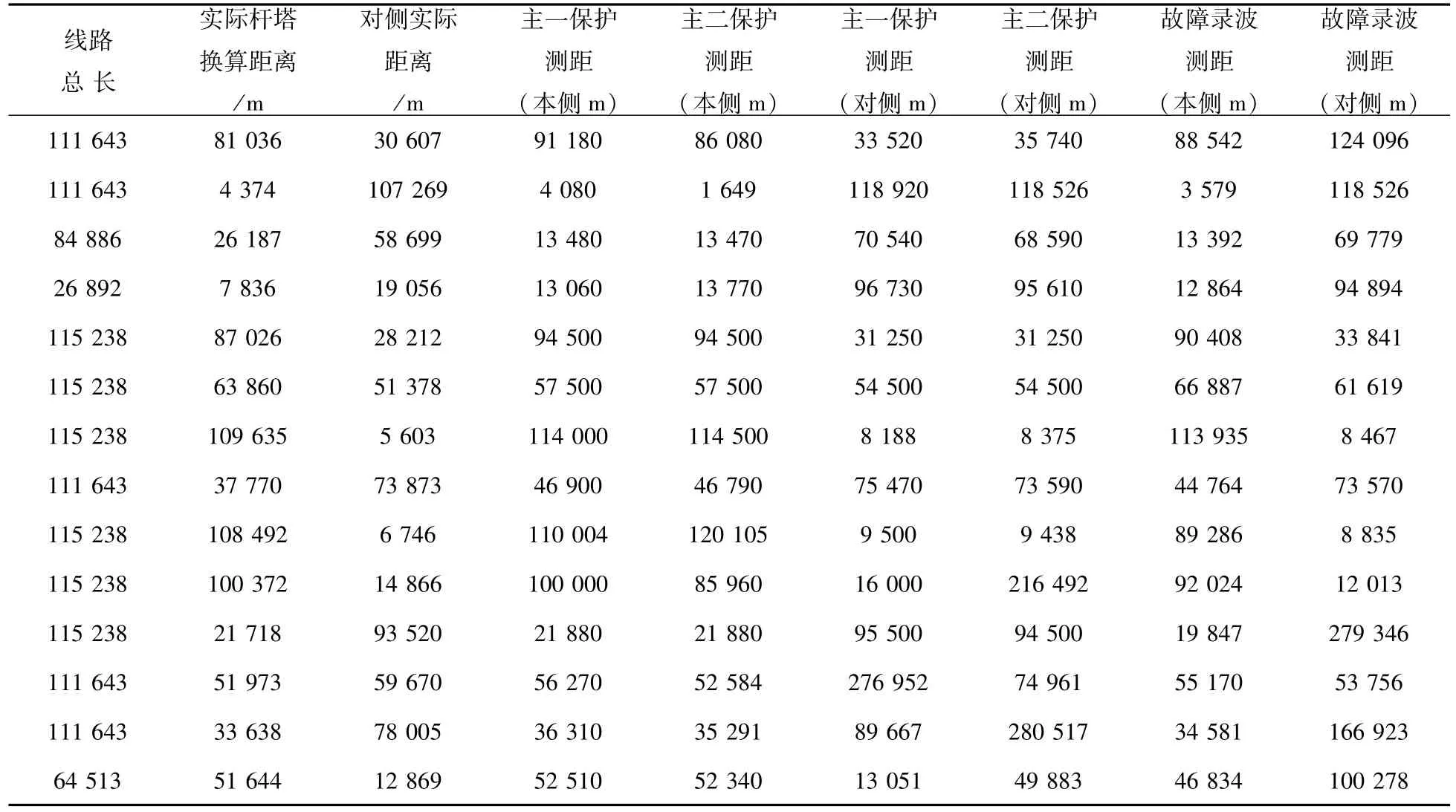
表5 220 kV系统雷击故障测距结果Tab.5 Distance measurement results of the lightning strike fault in 220 kV system

5 结束语

文章基于现有各种测距手段提供的测距结果信息，利用神经网络进行测距结果综合，以提高故障测距精度。所得主要结论如下：

（1）在各故障测距算法所得结果相差较小时，适宜采用综合模型1进行故障测距结果优化；而在各故障测距算法所得结果相差较大时，适宜采用综合模型2；

（2）无论是综合模型1还是综合模型2，均能有效融合各测距算法的测距结果，提高故障测距精度，且不受故障过渡电阻的影响，具有较好的工程实用价值。