500 kV变压器直流偏磁下的铁心损耗分析研究

赵欣，李强，叶红枫，山江川，刘念，王贺新

（1.四川大学电气信息学院，成都610065；2.中核核电运行管理有限公司，浙江海盐314300）

0 引 言

高压直流输电系统（HVDC）具有输送距离远，输送容量大等优点，输电方式有双极直流输电，单极直流输电和同极直流输电，因此产生的交直流系统间的影响日益明显［1］。高压直流输电系统采用单极—大地回线运行方式或双极地不平衡运行方式时，会有直流分量经大地进入到中性点接地的变压器中，发生直流偏磁，使得变压器铁心饱和程度增加，出现漏磁增大、损耗增加、局部过热、振动加剧和噪声增大等现象，严重时甚至可以对变压器本体造成永久性损坏［2］。此外，由地磁暴产生的地磁感应电流也可看作是诱发变压器直流偏磁的原因［3］。

目前，国内外研究者针对变压器的直流偏磁现象进行了大量研究，文献［4-5］分析了直流偏磁下变压器的磁通分布和励磁电流的畸变分析；文献［6］提出了一种采用磁化曲线比较方法不需外部建立复杂的直流系统模型来预测直流偏磁下的变压器的特性；文献［7-8］揭示了直流偏磁下不同磁化曲线对变压器铁心损耗仿真的影响。总之当变压器处于直流偏磁的情况下时，其铁心的铁磁材料表现出的电磁特性和标准测量条件下的电磁性能是有区别的，其中铁损的分布表现出与标准正弦激励条件下不同的规律［9］，由于铁心的损耗受偏磁影响尤为严重，剧烈增大的损耗将会导致铁心的局部过热和异常温升，导致铁心老化加重，因此需仔细分析铁心上的损耗分布和损耗变化，进而采取减少铁心损耗的措施，这对大容量超高压变压器的设计尤为重要。

针对某500 kV核电站主变进行分析，建立了基于二维有限元瞬态场A-φ算法下的变压器损耗模型，分析了直流偏磁下变压器的励磁电流的畸变；同时文献［10］中提出了一种通过划分变压器铁心路径的方式来分析自耦变压器磁感应强度的方法，在此基础上，针对的是普通双绕组变压器，并根据实际损耗仿真分布采用了具有针对性的铁心路径划分，进一步来分析直流偏磁下其铁心路径上的损耗的具体分布情况和增速的对比变化，并得到了不同的一系列结论，将对大容量超高压变压器的铁心设计和变压器直流偏磁铁心耐受能力分析提供一定的理论依据。

1 直流偏磁条件下的变压器模型

1.1 变压器的基本模型

文中分析的某核电站三相组式主变压器是由三个单独的单相变压器按照YNd11的联结方式连接组成，三个单相变压器的磁路彼此独立，互不相关，各相主磁通以各自铁心构成回路，且为了节约计算时间，可取三相中任意一相进行分析。则变压器的单相等效电路及磁路分析如图1、图2所示。

图1 变压器单相直流偏磁等效电路图Fig.1 Equivalent circuit diagram of single-phasetransformer under DC bias

图2 变压器磁路示意图Fig.2 Magnetic circuit diagram of transformer

若不计电源内阻和变压器铁心损耗，根据电路基尔霍夫定律、磁通连续性和安培环路定理可得电路方程和磁路方程为：

式中 R1、R2为变压器高低压侧绕组电阻；L1、L2为高低压侧绕组漏感；N1、N2为高低压侧绕组匝数；φ为磁通；i1、i2为高低压侧绕组电流，f1为铁心磁场强度和绕组电流的关系函数；f2为铁心磁场感应强度的函数。

1.2 直流偏磁条件下基于有限元法的变压器损耗模型

基于上述基本模型，采用二维瞬态场A-φ有限元算法来对其进行求解。首先把变压器的求解区域分成涡流区和非涡流区两部分，在涡流区（σ≠0）内，既要计算磁场，又要计算电场，所以同时采用矢量磁位A和标量电位φ来表述；在非涡流区（σ＝0）内，只需计算磁场，故用矢量磁位A来表述。

为了简化分析，并引入如下假设：（1）设电导率σ为常数，磁导率μ为常数；（2）不计位移电流，忽略绕组高次谐波；（3）只考虑变压器空载情况，由于空载电流很小，因此绕组上的铜耗很小，可忽略不计，即认为空载损耗为变压器的铁耗；（4）采用“均匀化”即将叠片铁心转换为均匀化的实体铁心；（5）考虑变压器的动态涡流损耗，静态磁滞损耗，则变压器的铁耗为二者之和。

建立麦克斯韦方程：

式中Js为源电流密度；Je为涡流密度；E为电场强度；B为磁感应强度；H为磁场强度；σ为电导率；μ为磁导率；ε为介电常数。Jf为绕组交流电流密度；Jb为直流偏磁电流密度。

因▽·B＝0，引入矢量磁位A，定义B＝▽×A。

则：

引入标量电位φ，有：

根据非正弦电流的复数表达形式和二维瞬态场的边界条件［11］，可将直流偏磁下变压器铁心内部瞬态场的求解转化为二维瞬态场矢量磁位微分方程边值问题：

式中Ω代表求解域；Γ1代表第一类边界条件；Γ2代表第二类边界条件。

对方程（7）中的三个等式，我们采用加权余量法和瞬态场的数值分析有限元法即三角形单元剖分法进行求解［12］。可得如下方程：

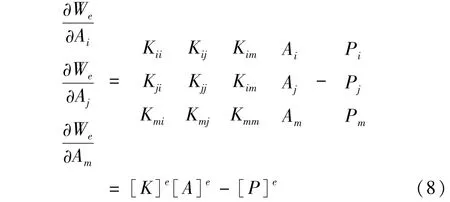
式中P为变压器铁心剖分单元的损耗值；We代表矢量加权函数；Ai，j，m，Pi，j，m代表三角形剖分单元下的磁位的插值矢量和损耗的插值矢量；Kii…mm代表单元形状系数。

再通过代数方法例如迭代法用计算机求解出方程组。即可得出单元内磁位A的值，磁感应强度B的值以及损耗P的值。

而导体区的总损耗Pw即变压器铁心的损耗则为各单元损耗P的迭加：

2 直流偏磁下变压器铁心损耗分析

在上述理论基础上在ANSOFT里按照1：1的比例构造出某一核电站500 kV变压器的直流偏磁模型。由于变压器结构对称，为了简化分析，仅在铁心左侧区域分别设置了A、B、C 3条垂直路径，铁心左侧上区域设置了D、E、F 3条水平路径，其中D、E关于主柱与上铁轭的交界面即主柱上边界对称；同时，分别考虑空载时不同直流电流即不同偏磁直流量的情况来分析变压器铁心的损耗分布。具体模型如图3所示。

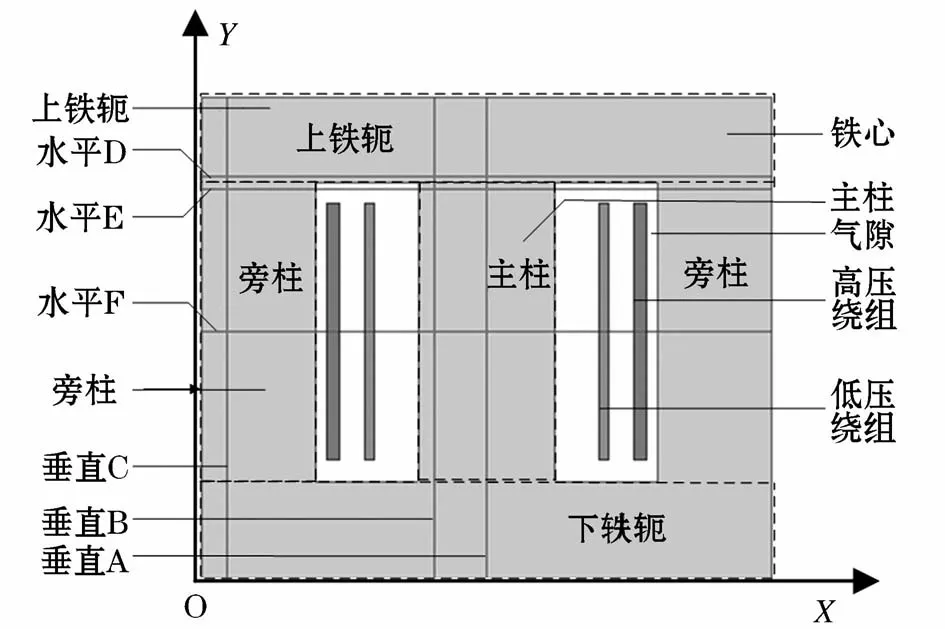
图3 变压器仿真模型和铁心路径分布Fig.3 Simulation model of transformer and the distribution of corn routes

已知变压器的二维实际尺寸为：长×高＝4 000×3 800（mm），则以上图所建立的变压器模型左下角为原点，以变压器的底侧边界长为X轴，以右为正方向，左侧边界高为 Y轴，以上为正方向，建立X-Y坐标系如图3所示，则不同路路径的具体位置如表1所示。

表1 不同路径的具体位置坐标Tab.1 Location coordinates of different routes

（1）直流偏磁时变压器的励磁电流分析

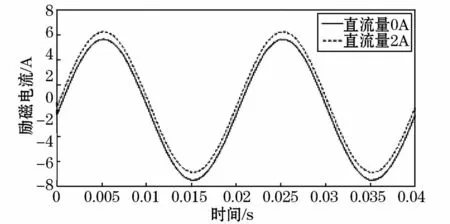
图4 励磁电流波形Fig.4 Waveform of the excitation current

根据上述模型仿真得到的500 kV变压器的励磁电流波形如图4所示。由图4可知，变压器没有发生直流偏磁（即偏磁直流量为为0 A）时，励磁电流的波形为正弦波且波形是关于正负轴对称的。但当变压器存在直流流入情况下即发生直流偏磁时，励磁电流波形畸变也越来越严重，关于正负轴出现不对称，波形向X正半轴出现向右的偏移，向Y轴正半轴出现向上的偏移。因此铁心在随时间交变的半个周期内饱和程度增加，励磁电流的畸变程度加剧，呈明显增大现象。

如图5所示，励磁电流发生畸变时各次谐波含量也发生了变化，没有发生直流偏磁时，谐波除了基波以外基本没有偶次谐波，只有少量的奇数谐波如3次谐波、5次谐波等；发生直流偏磁时，谐波除了基波、奇次谐波以外，还出现了偶次谐波。奇次谐波和偶次谐波都随着直流电流的增大而增加；并且偶次谐波增加的要比奇次谐波快的多，但是随着直流电流的增加，铁心到达饱和以后，各次谐波含量也开始下降。

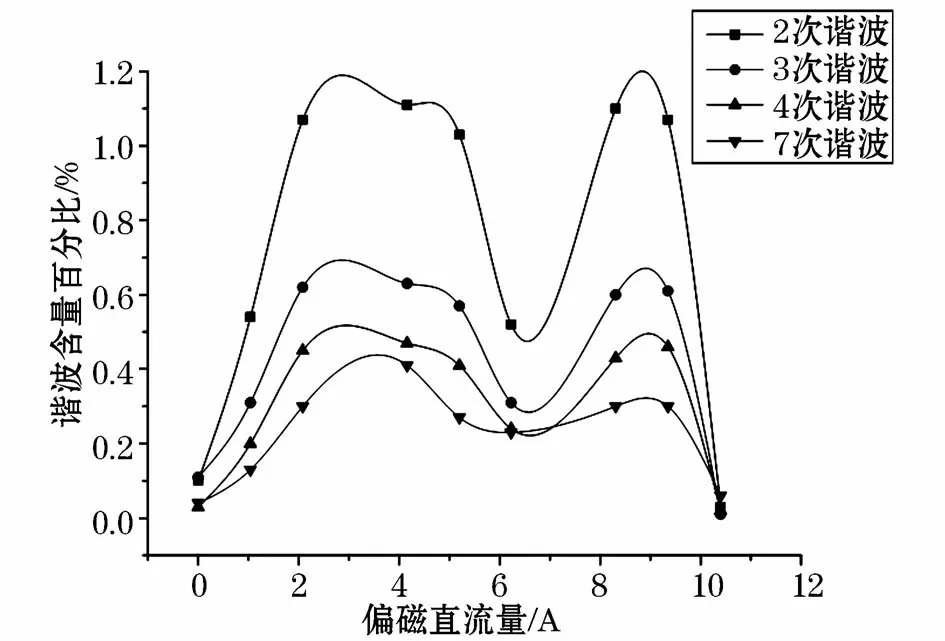
图5 励磁电流各次谐波含量Fig.5 Harmonic content of the excitation current

因此，综上所述，当变压器受到直流偏磁的影响时，其励磁电流会发生严重的畸变。励磁电流的畸变程度不等，会使得铁心磁致伸缩不均匀加剧，由此造成铁心局部的损耗增加和过热等，对变压器安全运行构成威胁。

（2）直流偏磁时变压器铁心的损耗分布变化

由上述分析可知，直流偏磁情况下由于励磁电流的畸变导致铁耗的分布不同，文章以偏磁直流量为5 A例，分析变压器铁心不同路径下的损耗分布情况。

由于励磁电源设置的初始角为90°（t＝0 s），而磁场最大值将滞后电压90°，励磁电流也大致滞后90°，所以在270°（t＝0.015 s）时磁场可达到最大值，损耗也可达到最大值，变压器将处于最严重的情况，因此截取此时的变压器直流偏磁为0 A和5 A时的损耗分布图来分析，如图6所示。从图中可直观看出，当变压器发生直流偏磁时，颜色较深即损耗较大的部位发生了转移，说明铁心上的损耗分布发生了变化。在无直流偏磁的情况下，损耗最大处出现在铁窗的尖角处；在有直流偏磁的情况下，损耗最大处却出现在上、下铁轭与主柱的交接处铁轭；且主柱和旁柱上的损耗分布也发生了变化。

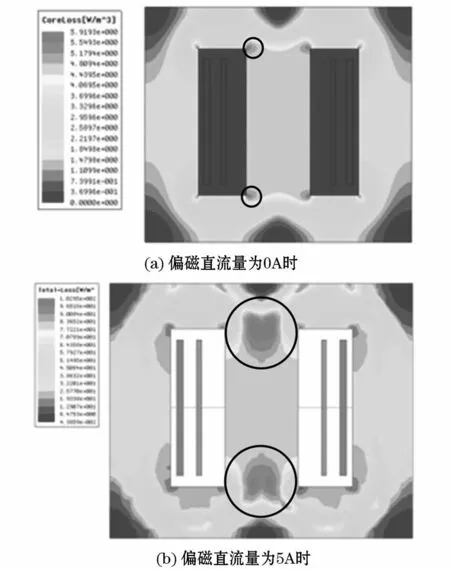
图6 直流偏磁下铁芯损耗分布云图Fig.6 Distribution cloud diagram of core loss under DC bias

为了进一步论证上述结论，将两种情况下铁心不同路径上铁耗具体分布进行数学处理，由图6观察可知铁心中部和铁窗附近的变化较大，因此通过文献［10］的路径分析法根据变压器实际损耗情况选取了垂直路径A和B，建立其路径距离和铁心损耗之间的关系，如图7所示可知。

从整体来看，在直流偏磁的情况下的铁损曲线明显地向Y轴正半轴有所移动，说明直流偏磁下铁心的损耗会有所增加。

单从垂直路径A分析，在无直流偏磁情况下，其路径上的铁心损耗分布是沿着铁心主柱递增，然后保持平缓后又开始递减，最大损耗平均分布在主柱区域，而在存在直流偏磁的情况下，其分布与无偏磁的情况相比，曲线中出现了两个波峰，且这两个波峰的位置靠近主柱和上、下铁轭交接的中部位置。

而单从垂直路径B来看，在无直流偏磁的情况下，在其靠近铁窗的位置出现了损耗的最大波峰，而在直流偏磁的情况下在其铁窗处却没有波动出现。

综上可知：在直流偏磁的情况下，铁心损耗的最大波动发生了转移，由铁窗附近转向铁心主柱与上、下铁轭交接处中部位置，同时结合图6（b）可知此区域也会有最大的损耗出现，则能进一步说明铁心主柱与上、下铁轭交接处受直流偏磁的影响最大。

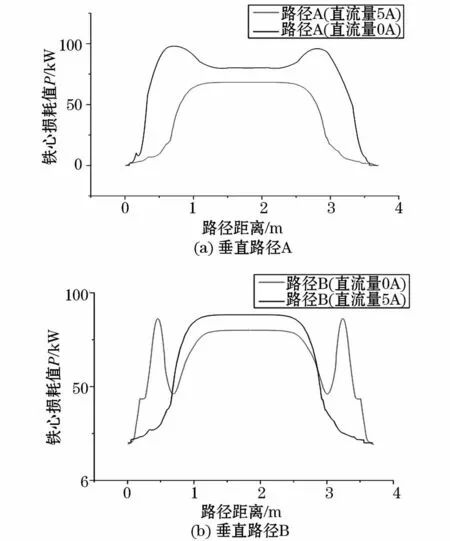
图7 不同路径下铁心损耗值随距离的变化Fig.7 Distribution of core loss variation with the distance in different routes

（3）直流偏磁时变压器铁心损耗增速变化直流偏磁时，铁心的损耗分布会有变化，同时其损耗的增速也会所有变化。

为了使研究问题一般化，文中采用不完全归纳法，选取了偏磁直流量为2 A、5 A、10 A、15 A、20 A、25 A、30 A时的铁心损耗与无直流偏磁情况下进行比较，由于单取一个损耗最大值Pmax可靠性不高，现用铁心单条路径上的最大平均损耗值Pavgmax来表征最大损耗值，即：

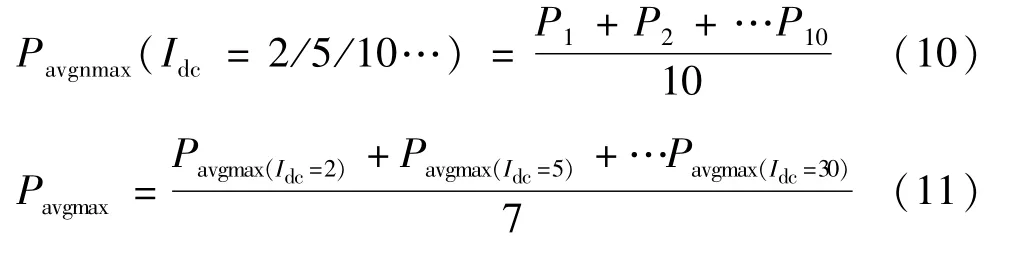
式中P1，P2，…P10为Pmax出现的前后抽取的10组不偏离±2%Pmax的损耗值。

方差可揭示样本内部彼此波动的程度，方差越大时，数据的波动越大；方差越小时，数据的波动就越小［13］。则可通过计算每条路径上其各种直流情况下各自Pavgmax的方差，来表征路径上损耗的波动大小同时，计算每条路径上的损耗增长速率即为每增加单位直流电流对应所增加的铁心损耗的平均值来反应对偏磁直流量的灵敏程度，V为单条路径增长速率有：

将垂直路径A、B、C和水平路径D、F的损耗值（由于D、E相似，因此只取一条路径分析）进行如上处理后如表2所示可知，水平路径上的损耗增速均高于垂直路径；水平路径受直流偏磁影响下的波动值也均大于垂直路径；最大增速、最大波动值均出现在水平路径D上；以上现象均能说明随着偏磁直流量的增加，水平路径上的损耗受偏磁直流量的影响较深，波动较大，灵敏度较高。

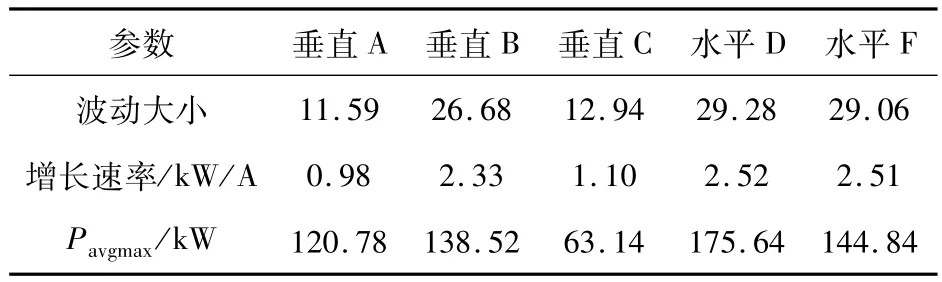
表2 不同路径损耗的波动大小和增长速率Tab.2 Variation sizes and growth rates of core loss in different routes

单独分析垂直路径A、B、C时，主柱路径A最大损耗值大于旁柱C，且二者增速差距不大，同时主柱路径B的损耗值和增速均远大于旁柱路径上的C的损耗值的增速。这就说明属于主柱路径损耗值和增速普遍大于旁柱路径损耗值的增速，而单独分析水平路径D、F时，随着偏磁直流量的增加，二者变化趋势类似。

3 结束语

文章基于二维有限元A-φ算法建立了变压器直流偏磁下的损耗模型，并通过仿真计算，得出以下结论：

（1）直流偏磁情况下，变压器的励磁电流波形的正负轴不再对称，谐波中会产生偶次谐波。

（2）直流量偏磁情况下，主柱与上、下铁轭交接处的铁轭区域受直流偏磁影响最深，损耗的最大值和最大增速均会向该区域中部转移。

（3）随着偏磁直流量的增加，主柱路径损耗最大值均高于旁柱，损耗增速普遍高于旁柱，水平路径的损耗增速和损耗最大值也明显高于垂直路径，说明水平路径和主柱路径损耗受直流偏磁的影响更深。