基于稳健回归的油浸式变压器表面温度预测
,
(湖南工业大学电气与信息工程学院,湖南 株洲 412000)
基于稳健回归的油浸式变压器表面温度预测
张伯伦,曾进辉
(湖南工业大学电气与信息工程学院,湖南 株洲 412000)
最小二乘法因为其简便、稳定的计算,在线性回归中应用非常广泛。但是误差项不服从正态分布,使用最小二乘法求解的回归模型可能会与真实数据存在严重偏差。针对经典最小二乘法的不足和局限性,本文提出一种基于稳健回归的方法来预测油浸式变压器表面温度。该方法采用迭代加权最小二乘法求解模型中的回归参数,选用Huber函数作为权函数,通过反复迭代,改变权重,最后得到一个行之有效的温度预测模型。该模型能够有效的剔除样本中的粗差,准确预测变压器正常运行时的表面温度。最后通过比较实测数据与预测数据,使用稳健回归方法得出的预测数据相比于最小二乘法的预测数据要更加接近于实测数据,验证了稳健回归方法用于油浸式变压器表面温度预测的有效性。
油浸式变压器表面温度;最小二乘法;稳健回归;Huber函数;迭代加权最小二乘法;温度预测
1 引言
大型电力变压器是输变电系统中的重要设备,绝大多数变压器的使用寿命终结是因其失去了应有的绝缘能力,而影响变压器绝缘能力的主要因素之一是变压器运行时的各个部件温升,根据GB1094.2—1996规定,变压器油箱及结构件表面温升上限为80K。为了能够在变压器各部件温升出现异常前发现温度异常问题,就需要对变压器正常工况下的表面温度进行预测,当预测的变压器正常运行表面温度与变压器实测表面温度的差值越来越大时,可认为变压器温度出现异常[1],可能会发生故障。
目前,为了能够预测变压器表面温度,国内外的学者专家提出的众多方法。如G.L.Alegi和W.Z.Black用试验的方法分析了热模型经验公式中的各项参数确定问题[2]。B.C.Lesieutre和W.H.Hagman等人在IEEE/ANSIC57.115的数学预测模型中加上环境温度因素,进一步优化模型[3]。He Q等人采用神经网络建模预测变压器顶层油温,并探讨了不同神经网络结构对于预测结果的影响[4]。ARRL De,CC De Azevedo和RM De Sousa采用遗传算法(GA)和粒子群算法(PSO)预测顶层油温,相比于多重线性回归有极大的改善[5]。
最传统的一般线性回归求解回归参数中,使用最普遍的是最小二乘法。但因为最小二乘法不具备抗差性,如果数据预处理做的不够好或根本没有进行预处理,导致样本中存在粗差,将会对回归参数的求解造成巨大影响。而稳健回归在数据量足够的条件下可以有效的减少样本中粗差对回归参数的影响,相比于数学探测法一次只能发现一个粗差的情况,稳健回归可以同时甄别出多个粗差并将其踢出。并且稳健回归不像最小二乘法那样要求参数求解在绝对意义上的最优 ,而是在抗差前提下的最优或接近最优,所以本文采用迭代加权最小二乘[6]的稳健回归方法来求解回归模型中的参数。通过比对供电局提供的实测值和采用稳健回归模型、一般线性回归模型得出的预测值,使用稳健回归模型得出的预测值更加接近于实测值,验证了稳健回归的有效性。
2 稳健回归理论
在目前的线性回归分析中,求解回归系数最常用的方法是最小二乘法,该方法仅仅要求误差项服从标准正态分布并且是相互独立的。而在生活实践中,并不是所有的误差都服从正态分布,其中不乏含有粗差[7],如果还是用最经典的最小二乘法计算回归模型参数,将会对模型的准确性产生严重影响,甚至导致错误。
针对上述不足,本文提出采用稳健估计的方法求解回归模型参数。当实测数据的误差项服从正态分布时,稳健回归和最小二乘法所求得的回归模型大致相同;当实测数据的误差项不服从正态分布时,稳健回归的求解准确度比最小二乘法的求解准确度要高很多。所以稳健回归能够有效的减少实测数据中所包含的粗差对回归参数求解的影响[8]。稳健回归的估计方法主要分为3类:M估计、L估计和R估计,目前最常用的是由Huber提出的M估计[9]。M估计的基本理念就是通过加权最小二乘法求解回归系数,依据残差的大小分配各点的权重,经过反复迭代计算,最终达到稳健的目的[6]。
对于线性模型:
(1)
式中,β0,…,βk为该模型的回归系数;e1,…,en独立同分布,均值为0;n为样本个数;l为自变量个数。用最小二乘法确定β0,…,βk,使残差平方和达到最小,其优化目标函数为:
(2)
由于最小二乘估计对每点的权重都是1,所以在观测数据存在粗差时,该点对残差平方和的影响非常严重,进而导致得出的回归模型与实际数据相差甚远。
本文采用迭代加权最小二乘估计,其优化目标函数[6,10]为:
(3)
对ρ(x)求导,并令其导函数为Ψ(x),式(3)对回归参数βk求偏导并令其为0,得到下式:
(4)

(5)
通过上述变换,将此转化为加权最小二乘回归的问题,目标是使∑[w(ei)ei]2达到最小。每点所赋予的权重大小根据该点残差大小来决定,残差大的赋予小权重,残差小的赋予大权重,由此建立加权最小二乘估计,通过多次迭代计算,重新分配各点权重,直至权重的改变量达到预先设置的容许范围内。
迭代加权最小二乘估计的计算方法如图1所示。
3 油浸式变压器表面温度的稳健回归模型
3.1 模型建立
结合大量文献资料[2-5,12-16],油浸式变压器表面温度与风速、环境温度、红外测温仪与油箱距离、母线电流有关。根据上述影响因素,可建立如下模型:
y=β0+β1x1+β2x2+β3x3+β4x4
(10)

图1 迭代加权最小二乘估计流程图
3.2 预测结果评价指标
温度预测的目的是利用有限个数的量测量获得接近于油浸式变压器正常运行时表面温度的真实值,评估算法性能优劣最直接的方式就是将预测值与真实值进行比对,对于不同的算法,可以采用总估计偏差(S1)和最大估计偏差(S2)两个指标来衡量算法的准确性。S1与S2的具体表达式如下:
(11)
(12)

4 实例分析
某变电站中有一台90MVA的双绕组油浸式变压器,电压等级为110kV,散热模式为自循环模式。根据变电站所提供的600组数据,现将数据分为两批,第一批共有500组数据,作为回归样本,用于估计回归参数;第二批共有100组数据,作为预测样本,用于评判预测模型的优劣性。
本文分别采用经典最小二乘法和稳健(Huber权函数)最小二乘法求解回归参数,结果见表1。

表1 经典法和稳健法求解回归参数
根据表1的结果,可以得出:在数据含有粗差的情形下,采用稳健回归估计比最小二乘估计得到的效果要好。从参数的显著性检验上来说,稳健回归估计所求解的回归参数都满足显著性检验的条件,而采用最小二乘估计得出的回归参数是不满足显著性检验条件的。
下面通过比较稳健最小二乘法和经典最小二乘法每次迭代计算后500组数据的因变量残差,如图2、图3所示。从图种可以清晰的看出,采用稳健最小二乘法计算回归参数时,只有极个别的因变量残差变化量很大,随着迭代次数的不断增加,因变量的残差逐渐减小;而采用经典最小二乘法计算回归参数时,因变量残差普遍较大,并且残差没有随着数据量的增加而减小。

图2 经典最小二乘法因变量残差

图3 稳健最小二乘法因变量残差
根据3.2中的评价指标(即公式(11)和(12)),可以得出表2。从表2中可以看出,经典最小二乘法总估计偏差S1要大于稳健最小二乘法的S2,这说明采用经典最小二乘法预测变压器表面温度时,产生的误差要比采用稳健最小二乘法产生的误差大。经典最小二乘法最大估计偏差S1要小于稳健最小二乘法的S2,这是由于在测试样本中编号为5和42号的实测数据中引入粗差。第42组数据中,粗差值为160℃,稳健最小二乘法预测值为96℃,经典最小二乘法预测值为145℃。粗差值与稳健最小二乘法预测值的差值(64℃)明显大于粗差与经典最小二乘法预测值的差值(15℃),由此可见,稳健最小二乘法的抗差性要由于经典最小二乘法。而在实际的变压器温度监测时,如果在某一时间点上,通过模型预测得到的变压器表面温度值与实际测量得到的变压器表面温度值的差值非常大时,则有很大的可能性是变压器出现故障,导致异常温升。因此,最大估计偏差S2对油浸式变压器的运行工况有一定的监测预警作用。

表2 经典法和稳健法的评价指标
现将用稳健最小二乘法、经典最小二乘法预测的数据与实测数据进行拟合,如图4所示。从图中可以看出,采用稳健最小二乘法预测的温度数据与实测数据更加拟合。第5组数据中,粗差值为54℃,稳健回归预测值为81℃,一般线性回归预测值为75℃;第42组数据中,粗差值为160℃,稳健回归预测值为96℃,一般线性回归预测值为145℃。从数据和图中可以看出,采用稳健回归得出的预测值与前后预测值相差不大,波动较小。而采用一般线性回归得出的预测值明显受到粗差的影响,较前后会有比较大的差别,波动很大,而且还会影响到粗差前后的预测值,从图中可以明显看到,第42组前后的数据中,由于粗差的影响,所有预测结果都偏大,严重偏离实测数据。由此可见,稳健回归方法能够有效的剔除数据中的粗差,还原事物本质,该方法要优于一般线性回归方法。
5 总结与展望
油浸式变压器的表面温度是电力变压器运行状态的重要指标之一。本文提出用稳健估计的方法来预测变压器表面温度,当预测的变压器正常运行表面温度与变压器实测表面温度差值越来越大时,则说明变压器温升存在异常。经过仿真试验验证,证明的该方法的可行性和优越性,经过反复迭代计算,改变权值,能够有效的排除粗差的干扰,具有良好的稳健性,克服了传统的最小二乘法权值都为1,无法剔除粗差的局限性。
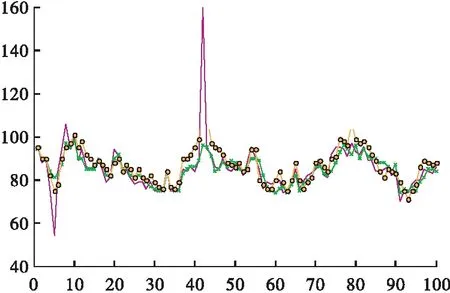
图4 稳健最小二乘法和经典最小二乘法的拟合比较图
本文也还有一定的不足,譬如本文中影响油浸式变压器表面温度的因素只考虑了风速、环境温度、红外测温仪与油箱距离、油箱体积这4项。在未来的研究中,影响变压器表面温度的模型中还将加入日照情况、负荷情况、季节变换等因素,进一步提高温度预测的准确性。
[1] 王红宇,苏鹏声,王祥珩,等.油浸式大型电力变压器表面温度预测模型[J].清华大学学报(自然科学版),2005,45(4):569-572.
[2] Alegi G L,Black W Z.Real-time thermal model for an oil-immersed,forced-air cooled transformer[J].IEEE Trans on Power Delivery,1990,2(5):991-999.
[3] Lesieutre B C,Hagman W H,Jr.Kirtley J L.An Improved Transformer Top Oil Temperature Model for Use in An On-Line Monitoring and Diagnostic System[J].IEEE Trans on Power Delivery,1997,1(12):249-256.
[4] Q H,J S,J T D.Discussion of _Prediction of top-oil temperature for transformers using neural networks_ and closure[J].IEEE Trans on Power Delivery,2001,4(15):1205-1211.
[5] De A,De Azevedo C,De Sousa R.Power Transformer Top Oil Temperature Estimation with GA and PSO Methods[J].Energy and Power Engineering,2012,1(4):41-46.
[6] 王少华,叶自强,陈金法,等.采用稳健回归算法的绝缘子污闪电压预测方法[J].电网技术,2010(12):131-135.
[7] 杨虎,钟波,刘琼荪.应用数理统计[M].北京:清华大学出版社,2006.
[8] Lawson C,Keats J B,Montgomery D C.Comparison of Robust and Least-Squares Regression in Computer-Generated Probability Plots[J].IEEE Trans on Power Reliability,1997,1(46):108-115.
[9] 王新军,黄守坤.预测型稳健回归模型及其实证分析[J].统计研究,2004(12):42-45.
[10] 张耀平,曹平,董陇军.岩石抗剪强度计算的稳健回归模型及其应用[J].科技导报,2010(7):91-95.
[11] Gastoni S,Granelli G P,Montagna M.Robust State-Estimation Procedure Based on the Maximum Agreement Between Measurements[J].IEEE Transactions on Power Systems,2004,19(4):2038-2043.
[12] Swift G,Molinski T S,Lehn W.A Fundamental Approach to Transformer Thermal Modeling-Part I:Theory and Equivalent Circuit[J].IEEE Trans on Power Delivery,2001,2(16):171-175.
[13] 尹克宁.变压器设计原理[M].北京:中国电力出版社,2003.
[14] 陈伟根,滕黎,刘军,等.基于遗传优化支持向量机的变压器绕组热点温度预测模型[J].电工技术学报,2014(1):44-51.
[15] 朱承治,郭创新,秦杰,等.基于DEPSO-RBFNN的变压器表面温度预测模型[J].电工技术学报,2008,23(6):37-43.
[16] Tylavsky D,He Q,Si J,et al.Transformer top-oil temperature modeling and simulation[J].Industry Applications IEEE Transactions on,2000,5(36):1219-1225.
Oil-immersedTransformerSurfaceTemperatureForecastBasedonRobustRegression
ZHANGBo-lun,ZENGJin-hui
(College of Electrical and Information Engineering,Hunan University of Technology,Zhuzhou 412000,China)
Because of its simplicity and stability,the least squares method is widely applied in the linear regression area.However,the error terms are not always strictly obey normal distribution,thus using the least square method to solve regression model may be inappropriate in consideration of the real data.In view of the shortage of the weighted least squares (WLS),this paper proposes a method that based on robust regression to predict the surface temperature of the transformer.This method uses the iterative WLS method to solve regression parameters and Huber function as the weight function.After a continually changing of the weights,an effective temperature prediction model was achieved.The model can effectively eliminate the gross errors in the samples and accurately predict the surface temperature of the transformer during normal operation.According to the comparison results between the measured and forecast data,the robust regression method can lead to a more accurate prediction of the surface temperature than the least-square method,which verifies the effectiveness of the proposed method in surface temperature prediction.
oil-immersed transformer surface temperature;least square method;robust regression;Huber function;iterative weighted least squares;temperature predictions
1004-289X(2017)03-0022-05
TM41
B
2017-02-17

