基于响应矩阵法的地下水系统开采方案
季叶飞,罗建男
基于响应矩阵法的地下水系统开采方案
季叶飞1,罗建男2
(1.水利部松辽水利委员会,吉林长春130021;2.吉林大学环境与资源学院,吉林长春130021)
文中选择响应矩阵法作为模拟优化模型的耦合集成方法,将其应用于地下水系统开采方案优选中。首先针对具体问题建立了地下水流数值模拟模型,并用GMS中的MODFLOW模块进行求解,在此基础上,应用响应矩阵法表示开采量与地下水位之间的关系,最后以开采费用最小为目标函数,考虑用户的用水需求以及周边的生态环境要求,建立优化模型并进行求解,得到了最优的开采方案及对应的最优开采费用。
地下水系统;模拟优化;响应矩阵
1 概况
由于地下水资源具有分布广泛,便于就地开采使用,水质普遍较优,动态比较稳定,供水量受气候变化影响较小等优点,使得地下水在总供水量中所占的比重不断提高,尤其是在干旱半干旱的北方地区,地下水是主要的供水水源。近年来,由于地下水的过量开采,引起了水资源枯竭、地面沉降、海水入侵等一系列环境地质问题。因此,合理地开发利用地下水资源,使有限的地下水资源发挥最佳的社会、经济效益,实现资源、环境、经济和社会的可持续发展变得尤为重要。地下水系统优化管理模型即为解决该问题的有效方法。
地下水系统的优化管理是以地下水本身固有的物理规律为基础,充分分析并描述地下水系统所面临的决策环境,通过地下水系统的人为可控输入策略的优化调控,使地下水系统的状态行为和功能效果按照所确定的目标达到最优的运筹过程。从地下水系统优化管理模型的构建上看,有3个组成部分:描述地下水系统输入与输出之间的响应关系的预测模型,描述地下水系统及其所面临的决策环境的优化模型,以及预测模型与优化模型的耦合集成技术。
最常用的模拟模型与优化模型的耦合集成技术为嵌入法及响应矩阵法。嵌入法是将地下水偏微分方程对空间和时间进行离散,形成一组线性代数方程,将这组方程式嵌入到优化模型中作为管理模型中的约束条件。这种耦合方法的优点是输出的信息多,缺点是当决策变量和约束方程多时,容易产生维数灾难,因此它仅适用于小规模的地下水管理问题。
响应矩阵法最早见于20世纪50年代末期石油工程的文献中,在建立寻求石油产量最大的线性规划管理模型中,采用响应矩阵表示油气田的压力随开采量的线性变化。响应矩阵法首先利用模拟模型计算出响应矩阵,然后利用响应矩阵所表示的约束条件计算管理模型,适用于大区域、多阶段的非稳定流地下水管理问题,在处理水文地质条件复杂、规模巨大的问题时,更能显示出优越性。
2 响应矩阵法
2.1 基本思想
响应矩阵法以线性系统的叠加原理为基础,运用地下水系统的模拟模型导出反映地下水系统特征的单位脉冲函数(系统的输出对系统的输入的响应关系),并形成其函数值的集合——响应矩阵。然后将它作为水均衡约束条件,结合地下水管理的其他约束条件及目标函数一起,构成地下水系统优化管理模型。
通常由偏微分方程及其定解条件构成的地下水系统模拟模型是一个非线性系统,不满足叠加原理,无法直接应用响应矩阵法。但可以从中分离出一个属于线性系统的子模型。即将地下水系统模拟模型拆分成:一个仅由人工可控输入作用而产生的降深S和人工流场;一个仅由初始条件、边界条件和不可控输入影响下形成的自然水位H和自然流场。在地下水资源管理中,人工流场模型主要用于求水位响应系数矩阵。人工流场和自然流场的叠加H-S=h即为自然-人工流场中的水位。
2.2 单位脉冲响应函数
对于一个线性的时不变系统,当给系统输入一个单位量的瞬时脉冲时,系统所产生的输出响应为单位脉冲响应。对于线性的地下水系统,把抽水作为输入,地下水位作为输出,则离散后的单位脉冲响应函数为:β(i,j,n-k+1) ,表示第j个结点在第k个时段以单位流量抽水,在第i点第n时段末所产生的降深。当在第j个结点上以Q(jk)在k=1,2,…,n时段连续抽水,则在第i个结点n时段末产生的累积降深为:

若同时有m个抽水井抽水,则产生的累积降深响应为:
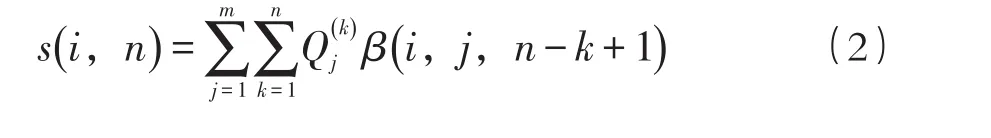
3 应用
3.1 实例简介
为了验证响应矩阵法在地下水系统优化开采中的应用,将其应用于一个假想例子中。
研究区为方形潜水含水层,长宽均为10 km。研究区西部是一个湖泊,平均水位为30 m;北部、南部及东部均为流线。各区渗透系数为K1=22.5 m/d,K2=25 m/d,K3=20 m/d;各区给水度均为0.3。参数分区及河流、排水沟和泉群的位置见图1,泉流量为1 000 m3/d。地下水接受大气降水入渗补给,补给强度为N=0.26 mm/d。
湖水水质恶劣,为防止地下水受湖水污染,要求距湖边1 km和2 km处的地下水位分别不低于31.5 m和32.5m。规划在结点11~20抽水,以供应结点15的用户,其总需水量第一年为5×106m3/a,第二年为5.5×106m3/a,单位输水费用为1.0万元/106m3,并随抽水点至用户的距离增加而增加,增长率为1.0万元/(106m3·km)。求在满足上述水位和需水量要求的条件下,使输水费用最小的开采方案。

图1 研究区示意图
3.2 地下水流数值模拟模型
3.2.1 水文地质概念模型
研究区目标层为非均质各向同性的潜水含水层。地下水在含水层系统中的运动为二维非稳定流,研究区内含水层系统的西部边界为一类边界,北部、南部及东部均为隔水边界。研究区的上边界为潜水面,是位置不断变化的水量交换边界,接受降水入渗补给;研究区的下边界为隔水边界。研究区内目前无开采,区内有河流入渗补给及排水沟和泉的排泄。假设研究区地下水位埋深较大,不考虑蒸发作用。
3.2.2 地下水流数学模型

根据水文地质概念模型建立相应的数学模型,包括偏微分方程以及定解条件。式中:D为地下水系统的模拟渗流区域;t为时间,d;T 为导水系数,㎡/d;η为给水度;Γ1为一类边界;Γ2为二类边界;W 为源汇项,m/d;h为地下水位,m。
3.2.3 数学模型的求解
选用美国Brigham Young大学的环境模型研究实验室和美国军队排水工程试验工作站开发的三维地下水数值模拟系统GMS(Groundwater Modeling System)软件中的MODFLOW模块进行求解。其求解方法是在模拟计算区域内采用矩形剖分和线性插值,应用有限差分法将上述数学模型离散为有限差分方程组,然后求解。
在空间上将渗流区剖分成10行10列,共100个矩形单元,每个单元为1 km×1 km。在时间上将模型分为2个时段,每个时段为365 d。
3.3 地下水资源优化管理模型
3.3.1 响应函数的确定
3.2.2 中所建立的数学模型是一个非线性模型。为了建立非线性系统地下水资源管理模型,将上面建立的水流模型分解为天然流场模型和人工流场模型:
天然流场模型
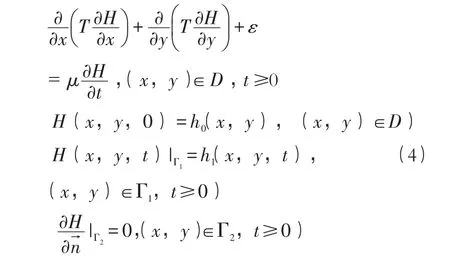
式中:H为天然水位,m;ε为不可控输入变量(降水蒸发等)。
人工流场模型(线性系统):

式中:P为可控输入变量(抽水量);S为降深,m。
由这2个模型所描述的流场叠加,即为由(3)所描述的自然—人工流场,其中h=H-S。
在不考虑人工开采的情况下,运行建立的模拟模型,得到不同时刻各水位控制点的自然水位H。
单位脉冲响应函数主要取决于地下水系统本身的特征,在求算单位脉冲响应函数时,抽水的单位流量一般以能使整个地下水系统内的各水位控制点处都有明显的响应值,且又不至于在系统边界处产生较大的影响为依据。据此原则,经过反复试算,此次脉冲量为10×105m3/d。
3.3.2 优化管理模型的建立及求解
目标函数:研究区地下水管理的目标是输水费用最低,即:

式中:Qkj为 j点在k时刻的抽水量,m3/d;cj为抽水费用,元/m3。
约束条件:
1)水位约束

式中:hni为i点在n时段末的水位,m。
对于线性含水层系统,水位降深和抽水量之间的关系,可以通过响应矩阵线性来表示,则含水层由各类人工抽水引起的降深可表示为:

因此,各水位控制点的水位可表示为:

式中:Hni表示第n时段末i点的天然水位,m。
根据式(8)及式(9),可将水位约束表示如下:

2)需水量约束

3)非负约束

式(6)(10)(11)(12)即构成了该问题的优化管理模型。该模型是一个有20个决策变量,62个约束条件的线性规划问题。用excel里面的规划求解对此模型进行求解。最优开采量见表1。

表1 两个管理时段不同结点的最优开采量m3/d
将决策变量的最优解带入到目标函数中得到最小的开采费用为621.64元/d,即22.69万元/a。
4 结论
响应矩阵法是一种有效的模拟优化模型的耦合集成方法,以其计算方便的特点广泛应用于地下水资源管理中。基于响应矩阵法的优化管理模型,求解得到不同时段各个节点的最优的开采方案,以及最优的开采费用(22.69万元/a),有效地解决了地下水资源开采方案优选问题,能够在节点水位满足约束条件下得到开采费用最小的修复方案,可以为地下水可持续开发利用提供依据。
[1]张晓烨,董增川.地下水模拟模型与优化模型耦合技术研究进展[J].南水北调与水利科技.2012,10(2):142-149.
[2]卢文喜.地下水系统的模拟预测和优化管理[M].北京:科学出版社,1999.
[3]李文渊.用响应矩阵法解地下水管理模型[J].武汉水利电力学院学报.1991,24(6):587-596.
[4]LeeA.S.,AronofskyJ.S.,A Linear Programming Model for Scheduling Crude Oil Production[J].Journal of Petroleum Technology,1958,10(7):51-54.
[5]辛欣.吉林西部地下水的模拟预报及管理模型探讨[D].长春:吉林大学,2008.
[6]李平.地下水管理模型中互馈关系协变理论和方法研究[D].长春:吉林大学,2008.
P641.8 < class="emphasis_bold"> [文献标识码]A
A
1002—0624(2017)12—0033—03
2017-04-20

