葡萄酒评价的差异性及可信度研究

毛园园

(东北石油大学数学与统计学院，黑龙江大庆163318）

葡萄酒评价的差异性及可信度研究

毛园园

(东北石油大学数学与统计学院，黑龙江大庆163318）

研究了两组品酒员对葡萄酒评价结果有无显著性差异及可信度。首先算出品酒员对每一类酒的每一项评价属性的平均分，然后将每一项的平均分与相应的权重做乘积，以每位品酒员作为基本单位将10项属性的分值相加得到的1个分值作为每一组的评价标准，即酒的质量。通过检验两个独立正态总体的关于均值是否相等的假设问题，得到葡萄酒评价结果有无显著性差异。采用比较标准差的方法来判断评价结果的可信度。

葡萄酒评价； t检验； 方差分析； 可信度

近年来，葡萄酒以其独特的口感和较高的营养价值得到越来越多消费者的青睐，而对葡萄酒质量的评价也日益成为人们关注的热点。评价葡萄酒的一般做法是由一批有经验、有资质的品酒员进行评定，评酒员凭借自身丰富的经验和敏锐的判断力对葡萄酒进行分指标打分，然后求其总分，确定葡萄酒的质量[1-3]。但这种评价方式容易受到诸多主观因素的干扰，比如品酒员所处的环境、当时的情绪状态和个人的意愿喜好等差异均会对评价结果造成影响，对同一批次的葡萄酒的评价结果往往出现分歧。品酒员所做出的判断应尽可能的客观公正、准确稳定，因为其评价结果无论是对葡萄酒生产者的质量监督还是对葡萄酒购买者的选择都具有重要的导向作用[4-5]。因此，为得到较为可靠的评价结果，需对品酒结果的差异性和可信度进行研究，以最终确定葡萄酒的质量。

1 数据预整理

根据相关数据可知，评酒员分别从葡萄酒的外观、香气、口感、整体4项对葡萄酒进行评价，总分值为100分。经观察，我们发现数据中存在3个奇异数，第1组第4个评酒员对红葡萄酒样品20在色调项没有评分，第1组第7个评酒员对白葡萄酒样品3的持久性项的评分为77分，第1组第9号评酒员对白葡萄酒样品8的持久性项的评分为16分，对这3个奇异值，我们均采用平均值来代替。

2 确定葡萄酒样本评分数据的概率分布

正态分布是一种最常见的连续型随机变量的分布，在实际的生产和科学实验中具有广泛的应用。对于大量个体的特性统计分析，可以尝试利用正态分布来估量。因此，可对葡萄酒样本的评分数据进行正态性检验，以判断该评分是否科学合理。

对每一个葡萄酒样品每组有10个评酒员对它进行打分，这10个评酒员的得分的平均值作为该葡萄酒样品的得分，即酒的质量，从而我们就得到总体Xi样本（Xi1，Xi2，……，Xi27）的观测值（i=1，2），同理，我们也得到总体Yi样本（Yi1，Yi2，……，Yi27）的观测值（i=1，2）。通过统计软件SPSS中的P-P图和单样本K-S检验方法[6]，对收集到的4组样本数据分别进行红、白葡萄酒正态分布检验，其结果见图1、图2。

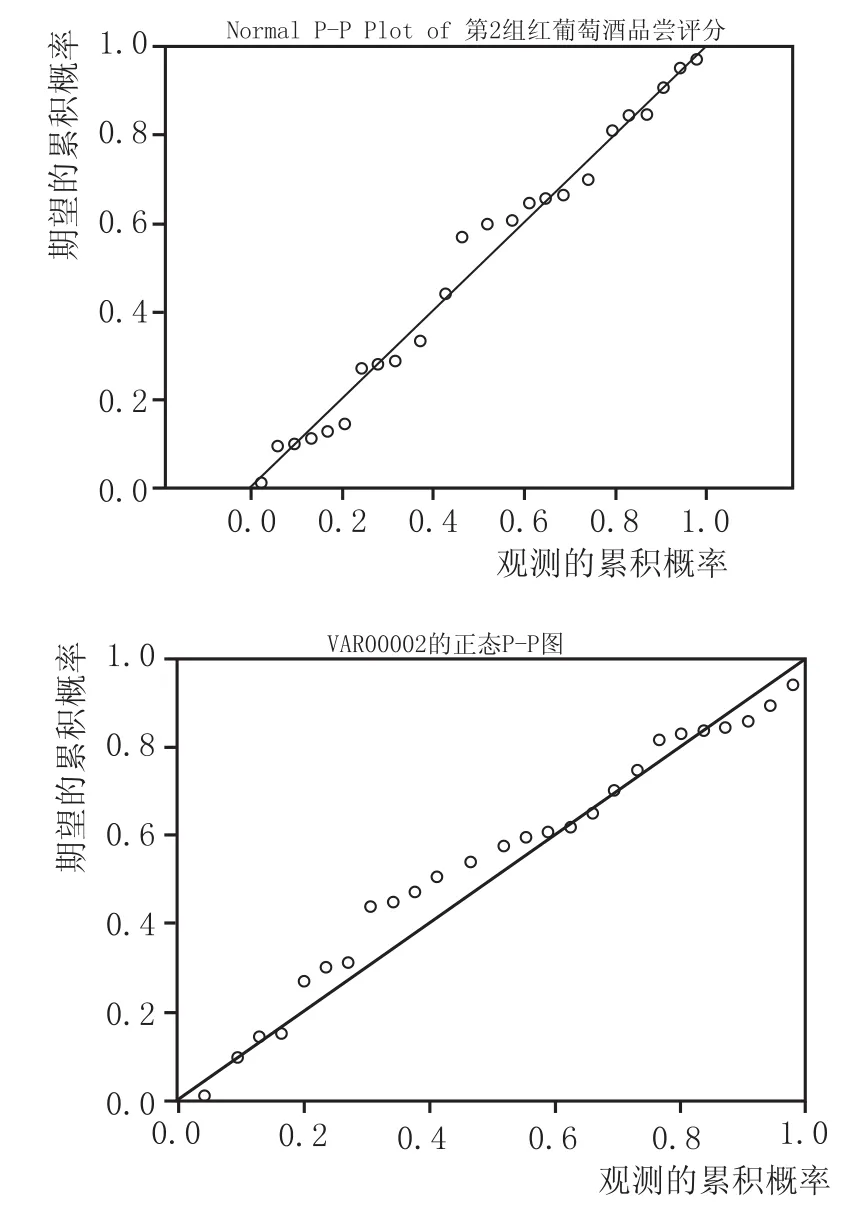
图1 第1组、第2组红葡萄酒评价结果的正态P-P图

从图2可明显看出，数据的散点分别近似为一条直线，且与对角线大致重叠，两组品酒员对葡萄酒的评分数据符合正态分布，结果见表1—表4。

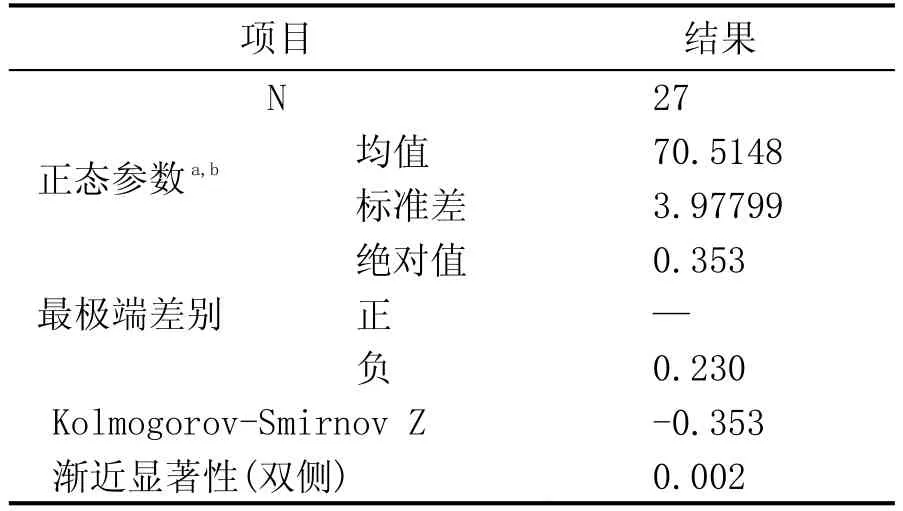
表1 第1组红葡萄酒评价结果的k-s检验结果

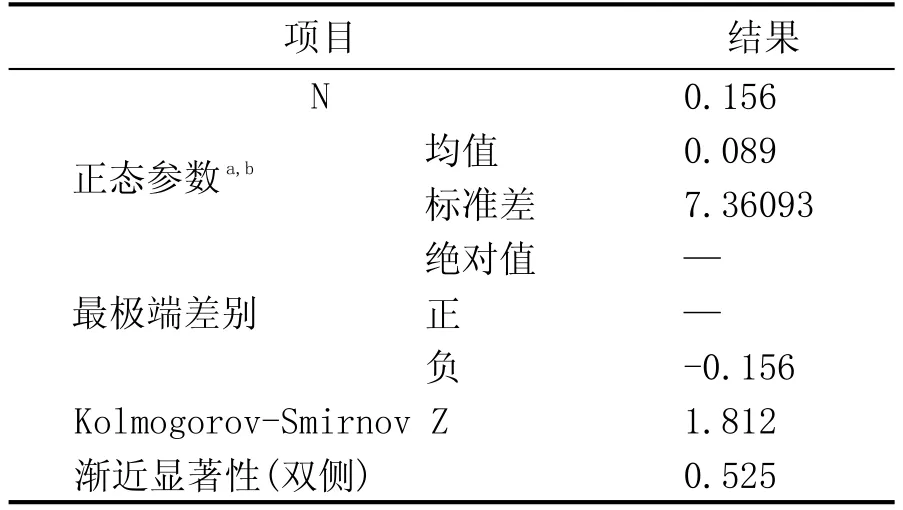
表2 第2组红葡萄酒评价结果的k-s检验结果

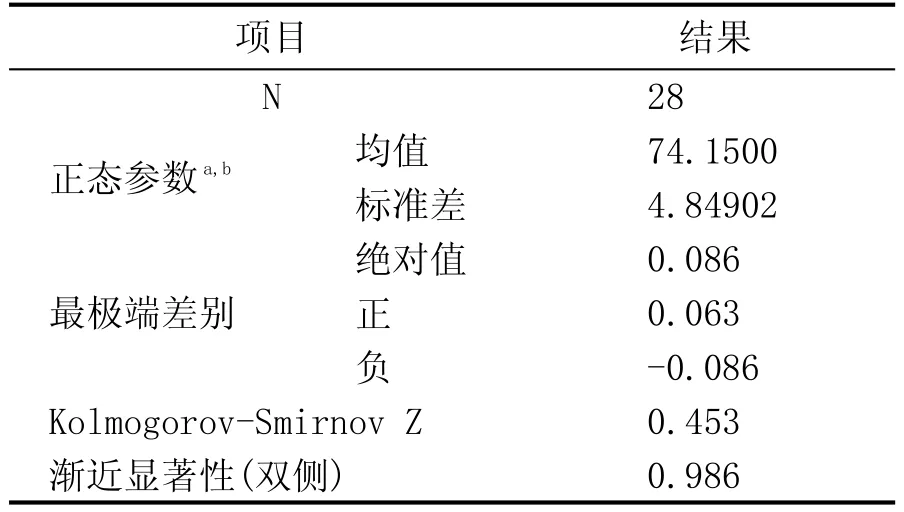
表3 第1组白葡萄酒评价结果的k-s检验结果

表4 第2组白葡萄酒评价结果的k-s检验结果

从表1—表4的k-s检验可知，双边检验结果均大于0.05，表明这4组样本数据均服从正态分布。为此我们假设总体Xi～N（μi，σi2）、Yi～N（ai，bi2），其中，μi、σi2、ai、bi2为未知参数。

3 评价结果有无显著性差异

为分析两组评酒员的评分是否科学和可信，需对评分结果进行显著性检验[7]。即检验这样一个假设：H0∶μ1=μ2，H1∶μ1≠μ2，是一个独立两个正态总体的关于均值是否相等的检验问题。

在检验假设H0∶μ1=μ2，H1∶μ1≠μ2之前，我们首先要讨论两总体方差是否相等[7]。?

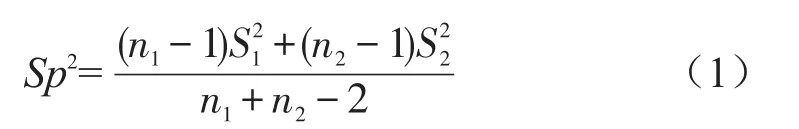
于是，用t统计量表示两总体均值差检验的检验统计量，表达式为：

当μ1-μ2=0（零假设），故可不考虑。在上述情?况（1）下（当时），t统计量服从自由度为n1+n2-2的t分布，t～tn1+n2-2；在情况（2）下（当时），服从定义如式（5）自由度的t分布，修正的自由度为[8]：

分别用F检验和t检验来判断两总体的方差和均值是否存在显著性差异[7]，并据此决定抽样分布的方差和自由度的计算方法和计算结果。在显著性水平a下，若F检验和t检验统计量的概率p值均小于a，则应拒绝原假设，认为两总体方差和均值都有显著性差异，此时t统计量的结果由式（2）和式（4）计算得出。相反，若两者概率p值均大于显著性水平a，则接受原假设，认为两总体方差和均值都没有显著性差异，此时t统计量的结果由式（1）和式（2）计算得出。

4 实现与结果分析

进行独立样本检验，使用统计学软件SPSS[9]，结果见表5。

表5 红葡萄酒的独立性检验结果

两总体方差有是否存在显著性差异的F检验。由表5检测结果可知，F统计量的观察值为3.341，概率p值为0.073。在显著性水平a=0.1情况下，可认为两总体的方差存在差异。

检验两总体均值是否相等，t统计量的观测值为1.488，概率p值为0.143，在显著性水平a=0.1情况下，由于概率p值大于0.1，则不能拒绝原假设，即此两组评酒员之间的评价结果没有显著性差异。因此取两组评酒员的得分的平均值作为红葡萄酒的最终评分。

同理，通过对白葡萄酒样本进行t检验，结果见表6。

表6 白葡萄酒的独立性检验结果

由表6检测结果可知，白葡萄酒两组样本数据的F统计量的观察值为4.185，相应的概率p值为0.046。在显著性水平a=0.1情况下，由于概率p值（0.046）小于0.1，故拒绝原假设，认为两总体的方差存在显著差异；再进行白葡萄酒两组样本数据均值差的检验，由式（3）和式（5）得t统计量的观测值为-2.347，在显著性水平a=0.1情况下，对应的双尾概率p值为0.023，概率p值小于0.1，同样拒绝原假设，即白葡萄酒两组评酒员之间的评价结果存在显著性差异。

5 可信度分析

可通过比较标准差大小的方法来分析两组评价结果的可靠性。方差的大小反映了品酒员之间对于样品酒评价的统一性，在无外界干扰的情况下，方差越小，说明评价越统一，进而说明结果越可信。由于每种酒的质量客观上已经是确定的，所以我们首先分别算出两组品酒员给出的每种酒样的每个属性20个分值的平均值，以此作为参考标准。再分别算出每一组品酒员对每一个属性评分的标准差，同种酒样的对应属性的标准差进行比较，在两组评酒员的评价结果无显著性差异。

所有的属性中统计标准差较小的那个属性个数，哪组的所统计属性多，我们判定该组品酒员对于此酒样的评价更可靠。重复此工作我们可以得出两组品酒员各自可靠酒样的数量，比较大小，认为所含可靠酒样数量多的组的评价结果更可靠。由于10属性可能出现每组标准差比较之后出现每组5个的情况，我们将每个酒样的总分也作为一个属性进行比较。

两组品酒员对红葡萄酒评分的总平均值：

两组品酒员对白葡萄酒评分的总平均值：

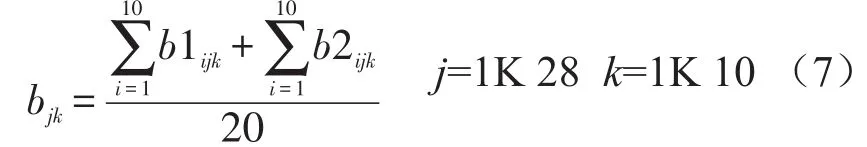
第1组品酒员对于红葡萄酒每个属性评分的标准差：

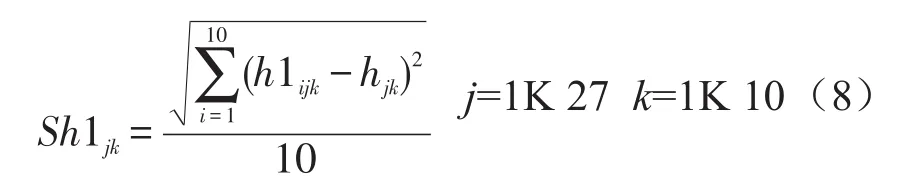
第2组品酒员对于红葡萄酒每个属性评分的标准差：

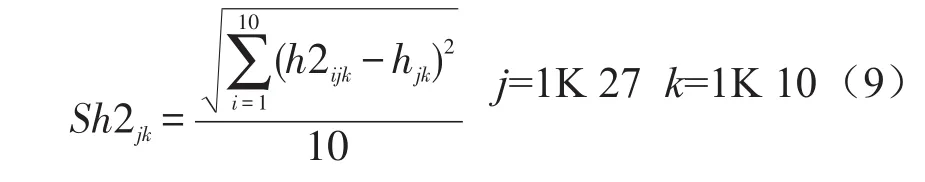
第1组品酒员对于白葡萄酒每个属性评分的标准差：

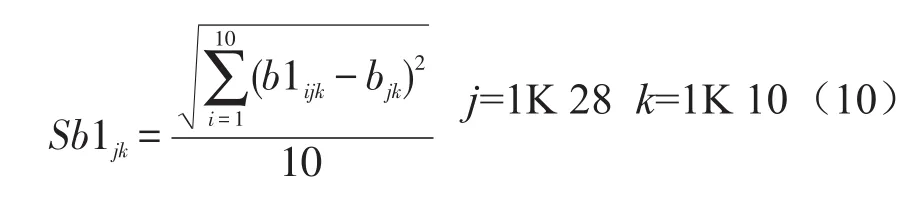
第2组品酒员对于白葡萄酒每个属性评分的标准差：

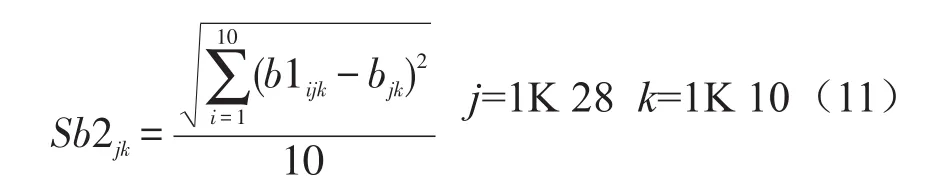
得到两组标准差首先对于表示每种酒样的属性进行比较，11对标准差作比较，标准差小的属性的数量越多的组，说明在此种酒中评分可靠，再对27种酒做整体比较，多数评分可靠，说明在整体中评分可靠。

结果分析：取第1种红、白葡萄酒作为示例，见图3、图4。

由图3可知，第2组的标准差较小的属性有6个，故认为第2组的评价更为可靠。

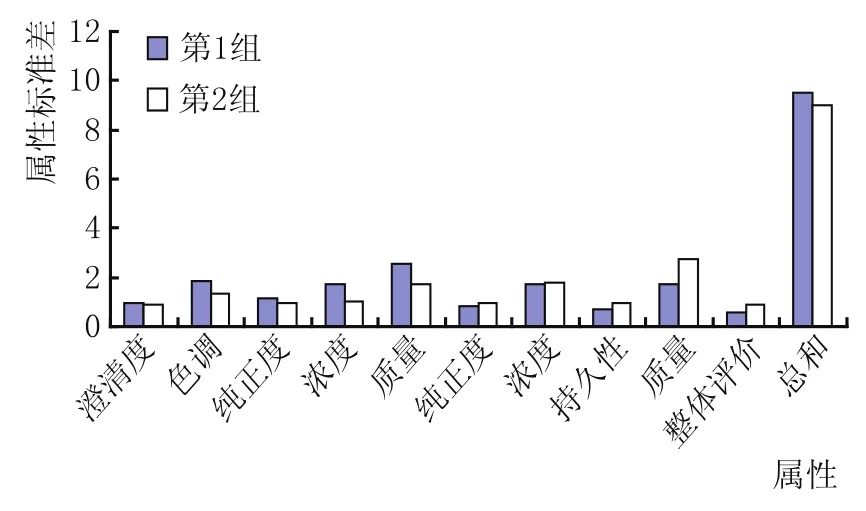
图3 红葡萄酒样品第1组、第2组的属性标准差

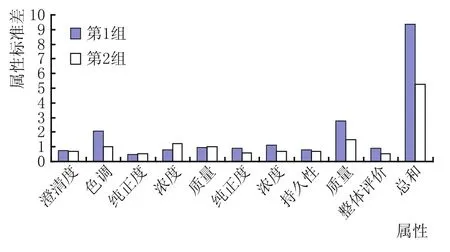
图4 白葡萄酒样品第1组、第2组的属性标准差

由图4可知，第2组的标准差较小的属性有8个，故认为第2组的评价更为可靠。重复该工作，统计每组可靠评价的酒样，结果见表7。

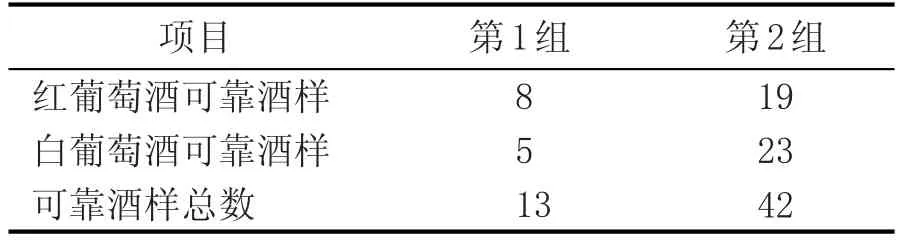
表7 两组可靠评价酒样的个数

由表7可知，红葡萄酒和白葡萄酒都是第2组的可靠评价酒样数远远大于第1组，故认为两种酒均是第2组的评价更为可靠。

6 结论

现有的葡萄酒评价方法带有很大的主观因素，本研究在对两组品酒员的评价结果进行分析与简单处理之后，运用t检验和比较组内标准差的方法，分别探讨两组样本数据的差异性和可信度，得到如下结论：首先，葡萄酒的样本数据服从正态分布；其次，通过检验两独立正态总体的均值是否相等，得到红葡萄酒的两组品酒员的评价结果没有显著性差异，白葡萄酒两组品酒员的评价结果有显著性差异；最后，利用反映波动的标准差来评价两组品酒员对葡萄酒打分结果的可信度，分析得出红葡萄酒和白葡萄酒都是第2组评酒专家的打分相对可信一些，因此取第2组评酒专家的得分作为红葡萄酒和白葡萄酒的最终评分。

[1]吴浩,靳保辉,陈波,等.葡萄酒产地溯源技术研究进展[J].食品科学,2014,35(21)：306-314.

[2]王华,赵现华,刘晶,等.葡萄与葡萄酒生产可持续发展研究进展[J].中国农业科学,2010,43(15)：3204-3213.

[3]李运,李记明,姜忠军.统计分析在葡萄酒质量评价中的应用[J].酿酒科技,2009(4)：79-82.

[4]高学峰,杨继红,王华.葡萄及葡萄酒生产过程中副产物的综合利用研究进展[J].食品科学,2015,36(7)：289-295.

[5]张苗苗,曹国珍,缪建顺,等.物理方法在酿造酒催陈中的研究进展[J].食品工业科技,2015,36(12)：395-399.

[6]何晓群.多元统计分析[M].3版.北京：中国人民大学出版社,2012.

[7]王创.统计假设检验中显著性水平α的选择[D].兰州：兰州商学院,2013.

[8]张凤菊,刘晓娟,赵丽平,等.数据差异显著性检验[J].农机使用与维修,2012(4)：51-52.

[9]滕冲,汪同庆.SPSS统计分析[M].武汉：武汉大学出版社,2014.

Difference and Reliability of Wine Evaluation

MAO Yuanyuan
(School of Math and Statistics,Northeast Petroleum University,Daqing,Heilongjiang 163318,China)

The study aimed at investigating the difference and the reliability of wine evaluation between two groups of wine judges.Firstly,the average score of each item for each type of wine was calculated.Then the average of each item and its corresponding weight worked out the product.With each wine judge as the basic unit,the score of ten attributes were added up as the standard score of evaluation for each group(namely,the quality of wine).Through the verification of the hypothesis-whether the mean of the two independent normal subjects was equal or not,we reached the conclusion that there was no significant difference in wine evaluation.Besides,the standard deviation method was adopted to judge the credibility of wine evaluation results.

wine evaluation;t test;variance analysis;reliability

TS262.6；TS971；TS261.7

A

1001-9286（2017）12-0032-05

10.13746/j.njkj.2017265

黑龙江省自然科学基金青年科学基金项目（QC2016002）。

2017-09-29

毛园园（1992-），女，硕士研究生，研究方向：统计学，E-mail：18645994523@163.com。

优先数字出版时间：2017-10-17；地址：http://kns.cnki.net/kcms/detail/52.1051.TS.20171017.1002.001.html。

2016年中国葡萄酒销量增幅全球第一

本刊讯：据《中国酒业新闻》报道，2017年11月13日，欧睿国际的统计数据显示，2016年亚洲葡萄酒销售达933亿美元或61亿公升，中国葡萄酒消费量初步统计达17.2亿升，增幅位居全球之首。

预计2016—2021年期间，亚洲葡萄酒销售额平均每年将增长8.5%，销售量则增长3.9%。此外，根据国际葡萄与葡萄酒组织(OIV)公布的数据显示，2016年中国葡萄酒消费量初步统计达17.2亿升，增幅位居全球之首。（江源荐，黄筱鹂编辑）

来源：中国酒业新闻 2017-11-15