基于最大期望和协同过滤算法的研究与应用
范 莹,郝琳娜,易 华,吉青晶,许华虎,尹方敏
(1.国家电网上海市电力公司培训中心,上海 200438;2.国家电网上海市电力公司检修公司,上海 200029;3.上海大学 计算机工程与科学学院,上海 200444)
基于最大期望和协同过滤算法的研究与应用
范 莹1,郝琳娜1,易 华1,吉青晶2,许华虎3,尹方敏3
(1.国家电网上海市电力公司培训中心,上海 200438;2.国家电网上海市电力公司检修公司,上海 200029;3.上海大学 计算机工程与科学学院,上海 200444)
推荐系统中新用户在信息搜索中易出现信息稀疏的问题,以致给用户推荐相关模块的时候带来了极大困难。针对该问题,采用人口统计学中的最大期望算法对用户进行聚类找到近邻用户,然后将其作为协同过滤算法的输入。由于用户对不同项目的评分表明他们需求,相同用户评价的项目中存在一定的需求关联性。而且随着个人需求的变化,这种关联度也逐渐在变化。所以通过引入一个时间权重函数的形式,给出一种基于用户需求变化的协同过滤算法,缓解传统协同过滤推荐算法的短板。可以追踪到用户的需求,进而预测评分矩阵。通过实验和比较,该算法有助于解决用户的评分矩阵稀疏性问题,从而提高推荐质量。
稀疏性;最大期望算法;协同过滤;个性化推荐
1 概 述
1.1 研究现状
处在如今这样一个大数据信息时代,用户对信息的需求得到了满足,但随着网络信息量的大幅度增长,使得用户在搜索信息时无法直接有效地获取到自己需要的信息,“信息爆炸”也因此而形成。数据挖掘网站逐渐兴起,协同过滤相关的推荐系统[1-5]在国外应用广泛,并取得了很高的应用价值。
国外著名的应用案例有协同过滤系统[6]和Amazon个性化系统[7]。Tapestry[6]是已知的最早投入使用的协同过滤系统,主要用于解决信息过载问题;Group Lens[8]通过用户-项目的评分矩阵来计算用户的相似性,寻找目标用户的最相似邻居的数据集,并根据这个数据集来产生推荐结果;Amazon个性化系统在给用户推荐个性化图书的同时,极大地提高了销售额。
国内的相关使用在近些年慢慢起步,研究水平和引用规模正逐年提升。国内比较好的应用[9]有互动出版网网上书店(http://www.china-pub.com/)以及网上文章推荐小助手(http://www.360doc.com/)等。互动出版网的会员[6]有一个“我的China-Pub”页面,上面记录会员用户的历史日志,会员还可以个性化定制个人的喜好;360doc通过对网站文章进行相关性分析和判断,在内容高度相关的文章间建立关联,能够看到很多“相关文章”。
1.2 存在的问题
在给用户提供个性化服务之前,大多数时候系统已经记录了用户的基本信息。但是新用户没有历史行为信息以供参考,因为新用户对系统里所有项目的评分都为空,也即是说新用户的可用信息是很稀疏的,因此无法获取到其需求点。文中采用人口统计学中的最大期望算法,把用户的基本信息数据源进行聚类,找到其近邻用户,然后将其作为协同过滤的输入。
在协同过滤推荐系统[10-11]中,基于用户的需求挖掘是个复杂问题,用户需求也就是对推荐项目的选择和偏好。但是这种需求可能会随着年龄、季节以及环境等的变化而变化。文中主要提出基于用户需求的协同过滤算法。该算法描述了用户需求的变换,可以预测用户项目的评分矩阵并进行补充。
2 最大期望算法
2.1 新用户的特征聚类
新用户在信息搜索的过程中会出现信息稀疏的问题,这会使系统给用户推荐相关模块时出现极大困难。文中引入人口统计学中的最大期望算法[12]来进行聚类,将用户的个人信息进行聚类分析[13-16],之后目标用户的邻居用户就能被找到,后续在协同过滤时将其作为用户集输入。
在用户聚类时,选用性别、年龄、职务、学历等作为特征维度。因为前人通过研究决策树技术发现这些特征信息对用户兴趣的偏好能产生较大影响。
2.2 最大期望算法聚类
在有了全部用户数据a的情况下,并不能确认他们来自哪个类别。若将用户的所有数据表示成(a,b),其中b代表a所属分支的标签,取值范围为b∈(1,…,θ)。此时,全部数据的概率密度[17]的定义为:
(1)
其中,θ为密度分支的个数;r1,r2,…,rθ(1,…,θ)为分支占总体分支的比例;fi为第i个分支的密度。
θi为相应分支的未知参数,在用户数据集{x1,x2,…,xn}确定之后,再用极大似然函数[18]估计的方法计算θmax:
(2)
最大期望算法[19-21]本质上是迭代算法,从初始解θ0迭代,陆续得到θ1,θ2,…,θt。在迭代过程中,似然函数的值一直递增。算法流程如下:
(1)给定一个初始化分布参数θ0;
(2)对每一个递增的θ1,θ2,…,θt,重复执行以下步骤直至收敛:
①给定用户数据和当前解θt,求用户数据的对数似然函数的期望值:

(3)
其在,Eb是关于随机变量b的期望。
②给定一个新的参数∂t+1,使得这时的对数似然函数期望值达到最大值:
∂t+1=argmaxQ(∂|∂t)
(4)
(3)一直循环迭代,可获得∂t,到最终算法收敛为止。
这样通过最大期望迭代自适应的计算,可得到各类用户簇和各个类别的分布特征。
3 协同过滤算法
3.1 项目评分矩阵
在推荐系统[22]中,用户集合U={U1,U2,…,Us}和项目集合I={I1,I2,…,It}间存在一个用户-项目评分矩阵,如表1所示。

表1 用户-项目评分矩阵Rs×t
其中,矩阵[23]共有s行,代表s个用户,t列代表t个项目。某个用户Ui对项目Ij的评分Ri,j代表用户i对项目j的偏好和兴趣。由于用户不可能对每个项目都有评分,所以在评分矩阵Rs×t中,有些评分是没有的,造成了用户-项目评分矩阵的稀疏性,使得用户间的相似度计算变得困难。
3.2 用户相似度计算
(1)标准余弦相似度计算用户相似性[23]。
(5)
因为通过标准余弦相似度[24]更多地是从方向上区别向量的不同,而且对绝对的数值不敏感,不能很好地衡量每个维度上数值的差异,从而造成巨大的误差。所以通过对所有的维度上的数值都减去一个均值来进行调整。
(2)调整余弦相似度。
为了调整因为不同用户对同种项目评分的偏差,通过对所有维度上的数值都减去一个均值来降低结果的误差。
Sim(Ua,Ub)=
(6)

3.3 用户需求变化问题
(1)基于时间的权重函数。
为了更好地观察用户的需求变化问题,提出一个时间权重函数TWF(u,i):

(7)
其中,tui表示用户u当前访问项目i的时间减去最近一次访问项目i的时间的差值; Ltui表示用户u当前访问项目i的时间与最远一次访问项目i的时间的差值;ε表示权重变化指数,ε∈(0,1),ε越大说明用户对项目i的关注越频繁。
(2)改进的余弦相似性。
在计算用户的相似性时,将用户-项目评分矩阵中的每一个评分值都乘上基于时间的权重函数,以获得更高的精度。

(8)
3.4 用户-项目评分预测
在用户相似度取得一个比较精确的值后,可以对用户-项目评分矩阵中没有的评分值进行预测。采用全局数值算法,以用户对相似产品的评分的相似度作为权值来生成预测评分。

(9)
其中,n为用户数量;Prai为用户a对项目i的预测评分。
4 算法设计和分析
4.1 算法步骤
输入:用户特征维度,用户-产品评分矩阵Rs×t,s个用户对t个项目评分的历史记录时间,时间权重指数ε;
输出:给用户的N个推荐项目。
Step1:利用给定的用户集合U={U1,U2,…,Us}和相关特征数据,通过最大期望迭代聚类找到目标用户的近邻用户,见式(3)和式(4);
Step2:利用用户-产品评分矩阵Rs×t和时间权重函数TWF(u,i),计算基于用户兴趣的评分相似性,见式(8);
Step3:在式(8)的基础上,采用全局数值算法对用户对产品的评分进行预测,见式(9)。
4.2 算法流程
如图1所示,用户登录系统后,首先判断其个人信息数据是否稀疏,看是否需要通过最大期望聚类操作来为其选取近邻用户。之后以此数据作为协同过滤的数据集,并根据用户-项目评分矩阵和时间权重函数计算基于用户兴趣的评分相似性,进而为目标用户进行资源推荐。

图1 整体框图
4.3 实验分析
4.3.1 评估标准
对于推荐系统的有效性,研究人员提出了许多评估标准来进行验证,大概包括两类:验证推荐结果的准确性;验证算法时间和空间的复杂度。平均绝对误差(MAE)能更好地反映预测值误差的实际情况,文中选择其作为评估标准。这种评估标准首先隐藏目标用户的真实评分,然后通过基于用户需求的协同过滤推荐算法预测其对项目的评分,最后通过预测值和真实值之间的差异累积得到平均绝对误差。
假设预测评分值为{p1,p2,…,pn},对应的真实评分值为{q1,q2,…,qn},通过式(10)计算得到平均绝对误差:

(10)
MAE的值与推荐的准确率呈反比。
4.3.2 数据源
选择网站http://grouplens.org/datasets/moviele-ns/上提供的数据集进行验证,提取该数据集中1 000个用户对1 700部电影的评分数据作为实验数据。
4.3.3 实验环境
实验环境如表2所示。

表2 实验环境信息
4.3.4 实验结果
实验结果如图2所示。
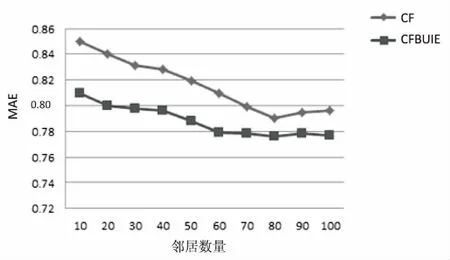
图2 MAE值比较
由实验结果可见,基于用户需求变化的协同过滤算法(CFBUIE)的精确性高于传统的协同过滤算法(CF)。
5 算法应用
5.1 应用设计
在上海市电力公司职工的“电力行业考试中心系统”在线版的基础上,实现了最大期望算法聚类和基于用户需求的协同过滤推荐相关算法。运用Android编程技术为其开发了移动端版本,将其在线版的数据移植到APP的版本上,在延续网页版的同时,为广大职工提供个性化推荐服务。整体流程如图3所示。
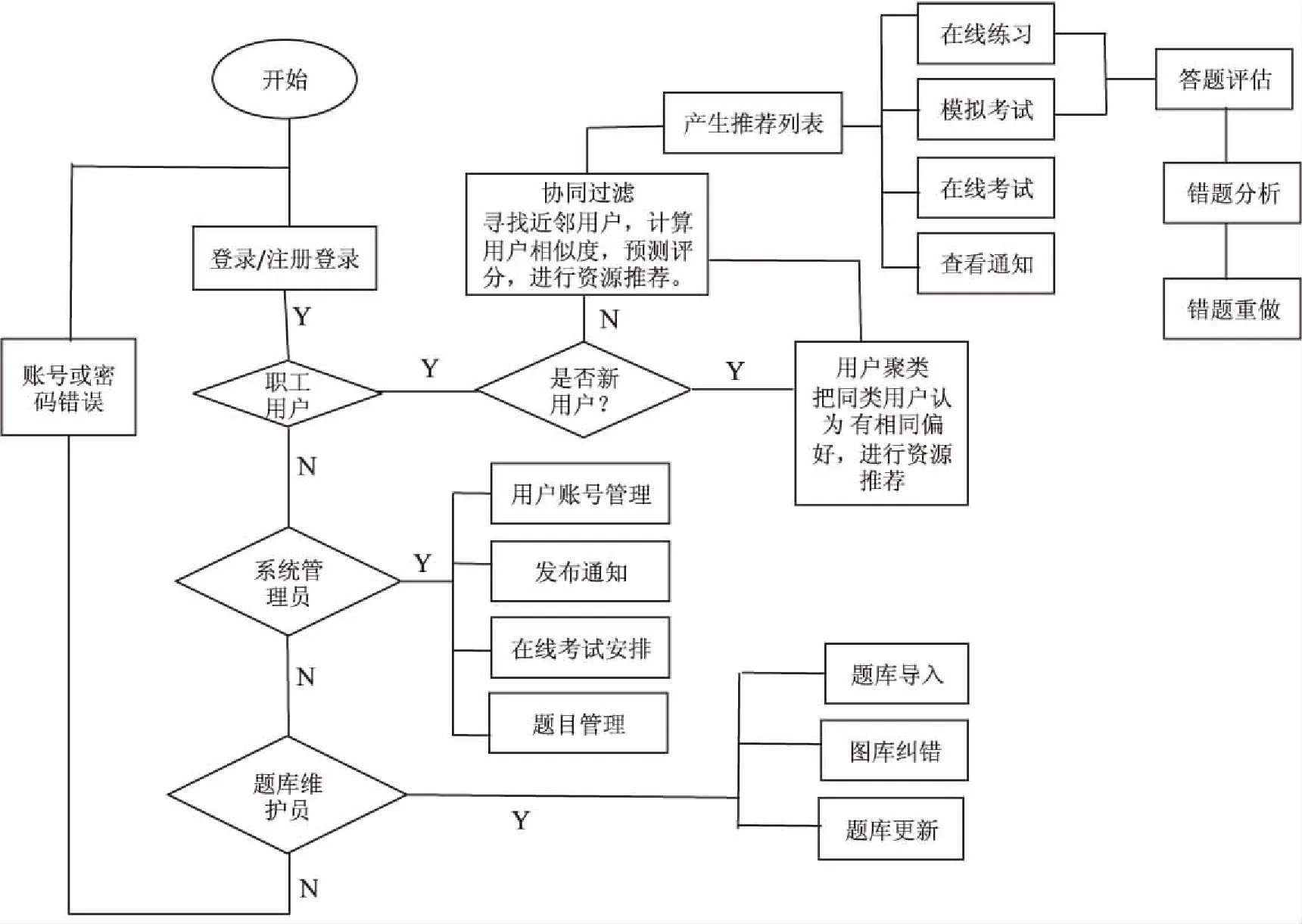
图3 整体流程
5.2 应用展示
Android应用界面如图4所示。功能涉及到考试学习的信息发布与管理,自助学习,自助练习,自助测试。移动平台可以建立针对个人的学习内容管理、学习进度管理、练习管理、练习成果分析、模拟考试等多种功能,能够满足用户的个性化需求。

图4 Android应用界面展示
6 结束语
针对新用户可用信息稀疏的问题,采用最大期望算法对用户进行聚类;针对现有协同过滤算法不能快速发现用户需求变化的问题,提出基于时间的数据权重函数,将其引进到传统的协同过滤推荐算法中以反映用户需求的动态变化,缓解了传统协同过滤推荐算法的短板,提高了推荐的准确性。今后会继续对相关算法展开研究,提高其使用范围,推广到各行各业。
[1] Tevreen L, Hill W,Amento B,et al. PHOAKS:a system for sharing recommendations[J].Communications of the ACM,1997,40(3):59-62.
[2] Shardanand U,Maes R.Social information filtering:algorithms for automating “word of mouth”[C]//Proceedings of the computer-human interaction conference.Denver:ACM Perss,1995.
[3] Rucker J,Polanco M J. Siteseer:personalized navigation for the Web[J].Communications of the ACM,1997,40(3):73-76.
[4] 简士尧.以内容为基础之网络学习导览推荐之研究[D].台湾:铭传大学,2004.
[5] Lieberman H,Dyke N W V,Vivacqua A S.Let’s browse:a collaborative web browsing agent[C]//International confer-ence on intelligent user interfaces.[s.l.]:[s.n.],1999.
[6] 孙小华.协同过滤系统的稀疏性与冷启动问题研究[D].杭州:浙江大学,2005.
[7] 杨 博,赵鹏飞.推荐算法综述[J].山西大学学报:自然科学版,2011,34(3):337-350.
[8] 冯旻远.综合用户特征的协同过滤推荐算法的研究[D].南京:南京邮电大学,2014.
[9] 涂金龙.基于tag的个性化推荐技术研究[D].重庆:重庆大学,2013.
[10] 张 驰,陈 刚,王慧敏.基于混合推荐技术的推荐模型[J].计算机工程,2010,36(22):248-250.
[11] Liu Z.Collaborative filtering recommendation algorithm based on user interests[J].International Journal of u- and e- Service,Science and Technology,2015,8(4):311-320.
[12] 刘 钢,王敏娟,张 驰,等.移动学习中的数据挖掘研究[J].中国远程教育,2011(1):31-35.
[13] 路东方,许俊富,项超娟,等.生物大数据中的聚类方法分析[J].上海大学学报:自然科学版,2016,22(1):45-57.
[14] 许丽利.聚类分析的算法及应用[D].长春:吉林大学,2010.
[15] 陈 俊,吴绍春,盛春健.基于概念格的聚类分析[J].上海大学学报:自然科学版,2008,14(4):432-435.
[16] 杜瑞杰.贝叶斯分类器及其应用研究[D].上海:上海大学,2012.
[17] 程剑锋,徐俊艳.基于EM算法的有监督LVQ神经网络及其应用[J].系统工程与电子技术,2005,27(1):121-123.
[18] 李 慧,马小平,胡 云,等.融合社会网络与信任度的个性化推荐方法研究[J].计算机应用研究,2014,31(3):808-810.
[19] 黄创光,印 鉴,汪 静,等.不确定近邻的协同过滤推荐算法[J].计算机学报,2010,33(8):1369-1377.
[20] 陈宗言,颜 俊.基于稀疏数据预处理的协同过滤推荐算法[J].计算机技术与发展,2016,26(7):59-64.
[21] 高 倩,何聚厚.改进的面向数据稀疏的协同过滤推荐算法[J].计算机技术与展,2016,26(3):63-66.
[22] 张拭心.余弦距离、欧氏距离和杰卡德相似性度量的对比分析[EB/OL].2013.http://www.cnblogs.com/chaosimple/archive/2013/06/28/3160839.html.
[23] 赵琴琴,鲁 凯,王 斌.SPCF:一种基于内存的传播式协同过滤推荐算法[J].计算机学报,2013,36(3):671-676.
[24] 吴想想.基于Android平台软件开发方法的研究与应用[D].北京:北京邮电大学,2011.
ResearchandApplicationofAlgorithmBasedonMaximumExpectationandCollaborativeFiltering
FAN Ying1,HAO Lin-na1,YI Hua1,JI Qing-jing2,XU Hua-hu3,YIN Fang-min3
(1.State Grid Shanghai Municipal Electric Power Company Training Center,Shanghai 200438,China;2.State Grid Shanghai Municipal Electric Power Company Overhauls Company,Shanghai 200029,China;3.School of Computer Engineering and Science,Shanghai University,Shanghai 200444,China)
The problem of sparse information is easily found in the information search for new user in recommendation system,and the difficulty is produced when recommending the relevant module for users.In view of the problem,the maximum expectation algorithm in demographics is adopted to cluster users for neighboring users,and then it is regarded as input of collaborative filtering algorithm.As the user’s scores on different projects show that they demand,in the evaluation of the project from same user there is certain demand relevance.And this kind of relevance degree is gradually changing with the change of individual demand.Therefore,a cooperative filtering algorithm based on the change of user demand is put forward by introducing a time weight function,which alleviates the shortness of traditional cooperative filtering recommendation algorithm.Can track the needs of users,and then predict the score matrix.According to experiments comparison,this algorithm can help solve the problem of sparseness of user’s scoring matrix and the recommendation quality is improved.
sparseness;maximum expectation algorithm;collaborative filtering;personalized recommendation
TP391
A
1673-629X(2017)12-0139-05
10.3969/j.issn.1673-629X.2017.12.030
2016-11-16
2017-03-22 < class="emphasis_bold">网络出版时间
时间:2017-08-01
国家自然科学基金资助项目(61572306,61502294);上海市自然科学基金(15ZR1415200);上海市科委重点项目(14590500500);2015年教育科研网-赛尔网络下一代互联网技术创新项目(NGII20150609)
范 莹(1987-),女,硕士研究生,研究方向为信息化技术在教育培训中的应用;许华虎,博士,教授,研究方向为多媒体网络技术、教育大数据。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170801.1551.040.html

