一种改进的LOF异常点检测算法
周 鹏,程艳云
(南京邮电大学 自动化学院,江苏 南京 210023)
一种改进的LOF异常点检测算法
周 鹏,程艳云
(南京邮电大学 自动化学院,江苏 南京 210023)
LOF异常点检测算法在实际应用中有两个缺陷:一是离群因子值只与参数K有关,当K取值不同时,离群因子的值将不同,之前是异常点的数据可能不再是异常点。二是对于未知异常点个数的数据集,选择参数K以保证离群点的挖掘数量合理难以做到。因此,提出一种结合平均密度的改进LOF异常点检测算法。首先分析数据集中数据点的平均密度,根据密度的分布情况确定数据集的异常点个数M1及异常集D1,然后通过计算离群因子确定M2(M2=M1)个异常点及异常集D2。取D1与D2的交集作为最终的离群集。实验结果表明,改进算法在检测精准性方面有显著提高,误报率较低,综合评价指标F值比LOF算法有显著增强。
LOF算法;平均密度;异常点集;离群因子
0 引 言
LOF(Local Outlier Factor)是一种常用的异常点检测算法。该算法通过计算数据集中每个数据点的离群因子值来确定异常点集,通常选取离群因子最大的若干个点作为异常点[1]。这种用离群因子来确定异常点的方法在已知异常点个数的情况下检测精确度很高。但实际应用中,异常点的个数可能事先并不知道,因此使用LOF算法来确定异常点集时,参数K的选择将显得十分重要[2]。当K选择不合适时,可能将大量正常的数据当作异常值,或将许多异常值归为正常值[3]。针对LOF算法的改进主要有三个方向:通过改进距离度量使密度更加合理;通过减枝降低算法的复杂度[4];人工获取最佳的K值[5]。这些改进算法提高了离群点检测的精确度,但对于离群点个数未知时,如何确定离群点的个数及离群集显得苍白无力。
1 LOF离群点检测算法
LOF算法是一种非常经典的异常数据挖掘算法,通过计算每个样本数据点的异常程度值来确定该点是否是异常点[6]。基于文献[7]的研究成果,局部异常点的异常程度和周围样本的分布情况有关。涉及到的几个定义如下:
定义1(K距离):数据对象q的k距离定义为数据集中到数据对象q距离最近的第k个点到q的距离,记作k-distance(q),这里的距离指欧氏距离即直线距离。
定义2(K距离邻域):数据集中与数据对象q之间的距离不大于k距离的数据点组成的集合,即
Nk-distance(q)(p)={p∈D{q}|d(q,p)≤
k-distance(q)}
(1)
定义3(可达距离):p,q为数据集中的任意两点,p到q的可达距离定义为:
reach-distk(p,q)=
max{d(p,q),k-distance(q)}
(2)
其中,d(p,q)表示点p和点q之间的欧氏距离。
定义4(局部可达密度):q的局部可达密度指q到其邻域内的所有点的平均可达距离的倒数。常用密度表示,计算方法如下:
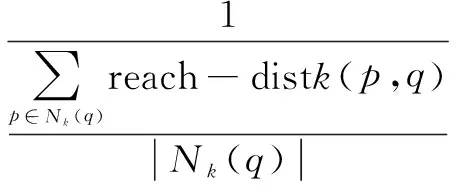
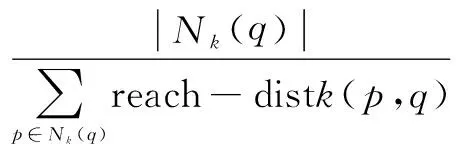
(3)
其中,|Nk(q)|为q的k邻域内的点的个数。由于可能存在若干个点到q的距离相等,故k近邻的点可能不止一个,所以有|Nk(q)|≥k。若lrdk(q)越大,表明q的密度越大,q点越正常。
定义5(局部离群因子):表征数据的离群程度,计算方法如下:
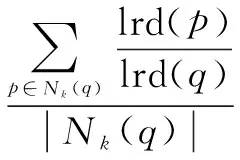
(4)
若LOF值远远大于1,表明q点的密度与整体数据密度差异较大,被视为离群点。LOF值越接近于1,表明点q越正常。
LOF算法的优点有[8]:
(1)算法将数据点q与周围k个点相结合进行分析,使最终获得的离群因子值更加合理,降低了密度极大值和密度极小值对整体数据的影响。
(2)采用数值的形式表示数据点的离群程度,更易于理解。
(3)只需设置一个参数k,易于操作和实现。
LOF算法的缺点包括[9]:
(1)若数据集确定,最终的离群因子值只和参数k有关。当k选择不同时,可能之前是离群点的数据样本现在不再是离群点。
(2)对于未知离群点个数的数据集,选择参数k以保证离群点的挖掘数量合理难以做到。
2 LOF相关改进算法分析
针对LOF算法的改进算法有很多。文献[10]将LOF算法的距离度量由欧氏距离改为和向量的内积有关的度量。将数据点x={x1,x2,…,xn}和y={y1,y2,…,yn}看成两个向量,则有

(5)
dist(x,y)=1-sim(x,y)
(6)
其中,dist(x,y)是数据对象x和y之间的距离。
同时对参数k设定一个范围,k∈[Minpts,Maxpts]。对于每一个k值,算法执行一次之后会获得一个离群因子值。针对k取所有可能值的情况下分别运行之后,对每个点获得的离群因子求均值。

(7)
文献[11]针对k距离的定义提出了改进,将k距离值定义为k个近邻点到中心点距离的均值。并对lrdk(q)重新定义,将q的k邻域内所有点的离群因子值的均值作为点q的离群因子值,如下所示:
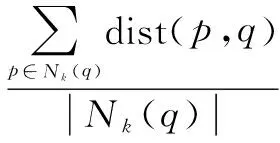
(8)
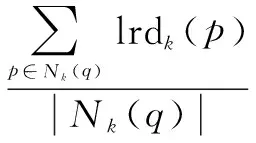
(9)
文献[12]采用剪枝的方式来检测离群点,改进了LOF算法的lrdk(q),并将其定义为数据点q的点密度,然后计算数据点q与其他数据点p的相异度。p到q的相异度为:
ddp→q=ρp·d(p,q)
(10)
则数据点p和数据点q之间的最大相异度为:
dpq=max{ddp→q,ddq→p}
(11)
然后表示出相异度矩阵DSM并生成无向连通图,根据相异度原理,若两个数据对象之间的相异度越大,则在无向连通图中它们之间的距离越远。接下来开始剪枝,首先剪距离最大的两个数据点,将其分成两个子树。遍历左右两个子树并继续剪枝。若最后削成的子树包含的节点小于k,则视为离群点。
相关的改进算法大多都是从距离度量方面以及最终离群因子的计算方面进行改进。文献[10]将密度和向量内积相结合,并给了k一定的范围。让k从最小值到最大值依次变化进行实验。优点是削弱k值对整个实验的影响,缺点是当k值变化范围较广时,实验次数较多,且当数据量巨大时,算法的时间复杂度会异常庞大。文献[11]提出的算法,用k个距离的均值作为k近邻,这样可以降低当数据中心点选择到那些可能是离群点的数据点时带来的误差。但当数据集的离群点个数未知时,该算法对如何选择合适的k值没有提出改进。文献[12]通过剪枝的方式获取离群点。依据数据点之间的相异度,将数据集表示成无向连通图,剪枝当前相异度最大的两个数据点。这种算法在剪枝的同时,还能获得不同类的数据集。该算法适合数据量较小的数据集。当数据量较大时,生成无向连通图的工作量将会很大,同时每一步只剪一枝。若离群点个数相对较少,则剪枝的次数将会很多,大部分的工作量将花在剪枝方面,算法效率不高。
当前的改进算法一定程度上提高了离群点检测算法的精确度,但对如何确定离群点的大致个数,即选择合适的k值,并没有提出改进方案。因此,文中接下来的内容是针对如何确定大致的离群点个数,以提高检测精确率。
3 基于平均密度和离群因子的LOF算法
对于一个只包含数值型数据的数据集D,若将每一条数据的属性看成是一个维度的话,则每一条数据可以映射成空间中的一个点。将数据集D中的所有数据进行映射,会得到分布在m维空间中的N个数据点。不同数据点周围的点分布多少并不相同,这就产生了一个数据分布点数差,即密度差。从数据的整体分布来看,数据点的密度不全相同,有的点密度较大,有的点密度较小。密度较大的点的个数会随着密度的增大而减少,而密度较小的点的个数也会很少(通常离群点都是存在于密度较小的点中)。大部分数据点的密度处于中间位置。
鉴于上述讨论,离群点总是存在于密度较小的数据点中。且由于离群点的个数相对整个数据集来说较少,故低密度点的个数也相对较少。因此,如果能够知道数据集中所有数据点的密度,做出密度个数分布图,就可以大致知道离群点的个数,同时可以获得离群点集D1。接下来调节LOF算法的参数k,使离群因子大于1的个数与密度个数分布图获得的离群点个数相当。这样,通过离群因子的计算可以获得离群点集D2。取D1与D2的交集作为最终的离群点集。
改进算法涉及到的定义及公式如下:
定义6(R邻域):以数据点q为中心,R为半径所构成的区域。
定义7(R邻域平均距离):R邻域内数据点到点q的距离的均值。
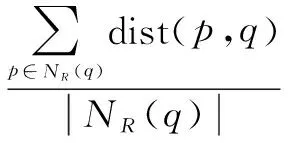
(12)
定义8(点密度):R邻域内点的个数与R邻域平均距离的比值。
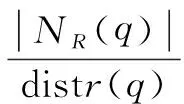
(13)
其中,|NR(q)|是q的R邻域内点的个数。
具体的算法步骤如下:
Step1:输入参数R,计算每个数据对象的R邻域点个数、R邻域平均距离及点密度。
Step2:找到密度跳变较大或密度对应的点个数跳变较大的位置。获取离群点个数M1及离群点集D1。
Step3:调节参数K,使离群因子值大于1的点个数为M1。
Step4:获取对应的M1个离群点集D2。
Step5:输出最终离群点集,D'=D1∩D2。
4 实验仿真
仿真使用开源数据集。开源数据集具有明确的标识,因此可以用来检测聚类、分类或离群点算法的精确度。
“牌手”数据集,是UCI数据库中用于检测分类算法精确度的数据集。它依据数据的密度分布将所有数据记录分为4类。为了验证文中离群点检测算法的有效性,随机取出500条第1类数据,然后从第2类数据集依次向第1类数据集中加入10、20、30、40条数据进行实验,由于第2类数据相比第1类数据具有异常特性,可以看作是异常数据进行挖掘。实验的测试环境是个人PC机,配置Intel Core2,T6500 2.10 GHz,2G内存,操作系统为Window7,编程环境为JAVA 8.0。
LOF算法与文中算法的检测结果如表1所示。
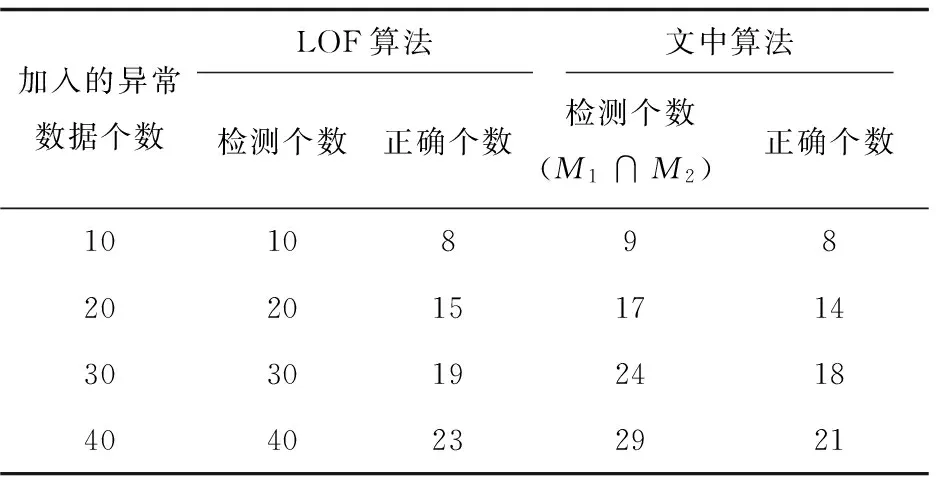
表1 LOF算法及改进算法的检测结果
计算两种检测算法的精确率P和召回率R以及加权评价指标值F[13]。有:
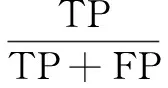
(14)
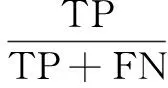
(15)
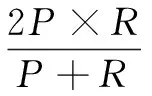
(16)
其中,TP为检索到的正确个数;FP为检索到的错误个数;FN为未检索到的正确个数;TN为未检索到的错误个数。
表2列出了两种算法的检测指标。
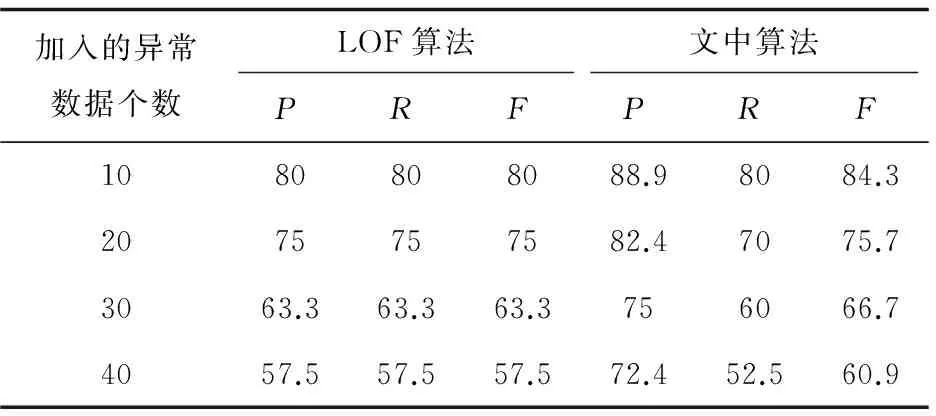
表2 LOF算法及改进算法的检测指标 %
图1为两种算法在不同异常数据下的F值曲线。
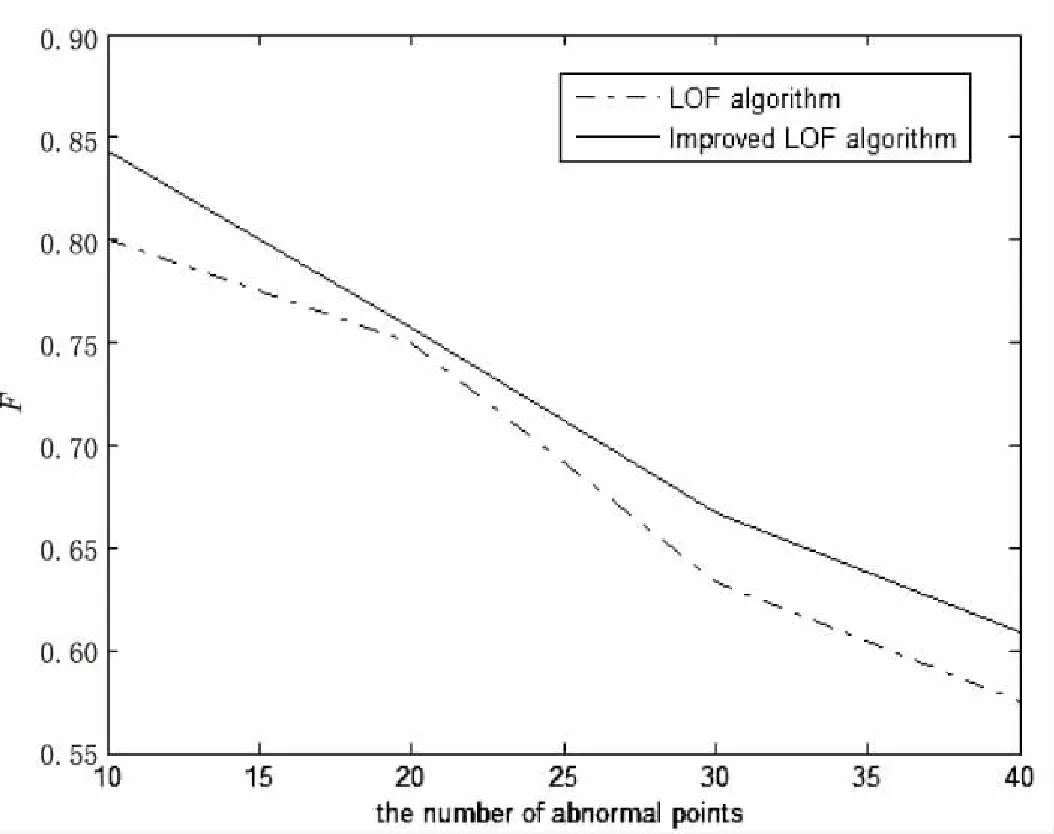
图1 评价指标值F曲线
文中改进算法根据数据的密度个数分布情况确定大致的离群点个数M1,并获得此时的离群点数据集D1。然后调节LOF算法的参数K,根据离群因子值确定M2(M2=M1)个离群点及离群数据集D2(离群因子大于1的M2个数据点)。取D1与D2的交集作为最终的离群集。
由实验结果可知,文中改进算法的精确率高于LOF算法,即误报率更低。但召回率略低于LOF算法,这仅仅说明LOF算法能够找到更多的异常值,但同时也引入了大量的非异常值。在许多关于离群点检测的应用中,要求快速检测出真实的离群点[14],从这方面而言,LOF算法虽然能够尽可能多地确定离群点,但其检测精度却不够高,这对于离群点检测而言是致命的打击。从图1可以看出,改进后的算法相比于LOF算法检测效率更高。加权评价指标值F越大,检测效果越好。此外,改进算法在确定异常数据的个数时,并不受真实离群点个数的影响,但结果却相对准确。因此表明改进的离群点检测算法同样适用于离群点个数未知的数据集。
5 结束语
在分析LOF离群点检测算法及其相关改进算法的基础上,提出结合数据分布平均密度的LOF算法。该算法一定程度上可以确定离群点的个数,同时取密度分布离群集和LOF异常因子离群集的交集作为最终的离群集。大大提高了检测的准确率,降低了误报率。从综合评价指标值F可以看出,改进后的算法综合准确率和召回率后,算法性能比单一的LOF离群点检测算法要好。
[1] 薛安荣,姚 林,鞠时光,等.离群点挖掘方法综述[J].计算机科学,2008,35(11):13-18.
[2] 闫少华,张 巍,滕少华.基于密度的离群点挖掘在入侵检测中的应用[J].计算机工程,2011,37(18):240-242.
[3] 徐 翔,刘建伟,罗雄麟.离群点挖掘研究[J].计算机应用研究,2009,26(1):34-40.
[4] 张卫旭,尉 宇.基于密度的局部离群点检测算法[J].计算机与数字工程,2010,38(10):11-14.
[5] 王 茜,刘书志.基于密度的局部离群数据挖掘方法的改进[J].计算机应用研究,2014,31(6):1693-1696.
[6] 杨风召,朱扬勇,施伯乐.IncLOF:动态环境下局部异常的增量挖掘算法[J].计算机研究与发展,2004,41(3):477-484.
[7] BREUNIG M M,KRIEGEL H P,NG R T,et al.OPTICS-OF:identifying local outliers[M]//Principles of data mining and knowledge discovery.Berlin:Springer,1999.
[8] 王 飞.iLOF*:一种改进的局部异常检测算法[J].计算机系统应用,2015,24(12):233-238.
[9] 肖 辉,龚 薇.基于可达邻域的异常检测算法[J].计算机工程,2007,33(17):74-76.
[10] GUAN H,LI Q,YAN Z,et al.SLOF:identify density-based local outliers in big data[C]//Proceedings of web information system and application conference.[s.l.]:IEEE,2015:61-66.
[11] SALEHI M,LECKIE C,BEZDEK J,et al.Fast memory efficient local outlier detection in data streams[J].IEEE Transactions on Knowledge and Data Engineering,2016,28(12):3246-3260.
[12] 杨茂林,卢炎生.基于剪枝的海量数据离群点挖掘[J].计算机科学,2012,39(10):152-156.
[13] JIANG M,FALOUTSOS C,HAN J.CatchTartan:representing and summarizing dynamic multicontextual behaviors[C]//ACM SIGKDD international conference on knowledge discovery and data mining.[s.l.]:ACM,2016:945-954.
[14] 闫 伟,张 浩,陆剑峰.一种离群数据挖掘新方法的研究与应用[J].控制与决策,2006,21(5):563-566.
AnImprovedLOFOutlierDetectionAlgorithm
ZHOU Peng,CHENG Yan-yun
(School of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)
In practical application,LOF,an anomaly detection algorithm,has two defects.One is the outlier factor value only related to the parameterK.WhenKis changed,the value will be different from before and an abnormal point may be a normal point.Another is for a data set with unknown abnormal points.It is very hard to choose a suitable parameterKto ensure reasonable mining number of outlier points.Therefore,an improved LOF combined with the average density is proposed.Firstly,the average density of each point is analyzed,and the number of abnormal points (M1) and abnormal set (D1) are determined according to the distribution of average density in the data set.ThenM2(M2=M1),another number of abnormal points,andD2,another abnormal set,are ensured through calculating the value of outlier factor.The intersection ofD1andD2is taken as the final result.Experiment shows that the improved algorithm can improve the detection precision remarkably with lower false rate,and is superior to LOF on the comprehensive evaluation indexF.
LOF;average density;abnormal point set;outlier factor
TP181
A
1673-629X(2017)12-0115-04
10.3969/j.issn.1673-629X.2017.12.025
2016-12-19
2017-04-26 < class="emphasis_bold">网络出版时间
时间:2017-09-27
江苏省自然科学基金(BK20140877,BK2014803)
周 鹏(1991-),男,硕士研究生,研究方向为数据挖掘与智能计算;程艳云,副教授,硕士生导师,从事自动控制原理、网络优化的教学科研工作。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170927.0958.030.html

