基于ELM-AE的二进制非线性哈希算法
邓万宇,张 倩,屈玉涛
(西安邮电大学 计算机学院,陕西 西安 710000)
基于ELM-AE的二进制非线性哈希算法
邓万宇,张 倩,屈玉涛
(西安邮电大学 计算机学院,陕西 西安 710000)
21世纪是数据信息时代,移动互联、社交网络、电子商务大大拓展了互联网的疆界和应用领域,由此而衍生的各类数据呈爆炸式增长,使得传统的数据分析手段已无法进行有效的数据分析。为了有效解决大规模图像数据的高效检索问题,满足大规模图像数据库的实际应用需求,提出一种基于快速极限学习机自编码(ELM-AE)的哈希二进制自编码算法。算法通过ELM-AE对数据样本进行优化,提升了图像检索的效率;通过二进制哈希实现高维图像数据向低维的二进制空间的映射和重表,提高了图像检索的精度和效率;此外,通过非线性激励函数解决了线性函数在处理非线性数据时的局限。实验结果表明,基于ELM的二进制自编码哈希算法在运行时间等方面有着良好的表现,取得了良好的检索效率和精确度。
哈希学习;自编码;极限学习机;图像检索;机器学习
0 引 言
随着数据信息时代的到来,移动通信、社交网络、电子商务大大拓展了互联网的疆界和应用领域,由此而衍生的各类数据呈爆炸式增长。在各类数据中,图像由于携带信息丰富、表现形式直观等特点,成为人类传播信息中最为有效的媒介之一,在科学研究、人类生活、工业生产等诸多领域占据着重要地位。例如,一项针对社交网站Facebook的调查显示,用户在短短七天内就上传了7.5亿幅图像,而Facebook开放至今已经累积了2 400亿幅图像。此外,图像编码方式的不同、图像本身的非内容修改(如添加字幕或嵌入数字水印等)以及图像的再版等因素,导致网络上出现了很多重复的图像,这给图像检索增加了难度。因此,面对图像数据规模的爆炸式增长,如何针对大规模图像进行快速而准确的检索,是众多图像处理与挖掘任务的先决条件。
为满足大规模图像数据库的实际应用需求,解决图像检索面临的难题,主要方法有两种[1]:提取有效的图像特征,降低图像特征冗余;将图像特征转化为紧凑的表现形式,实现用少量的数据即可表现原图像中的重要信息,从而实现图像快速精确的相似性检索。
近年来,哈希学习算法[2-7]由于其优越的计算和存储性能,受到了学者们的广泛关注。哈希学习主要通过保持数据的相似性信息,将原始的空间数据映射到低维的汉明空间,得到紧致的哈希码。通过计算汉明距离,能快速返回相似性结果;同时,只需要存储哈希码而非原始数据,存储空间大大降低。例如:局部敏感哈希(Local Sensitive Hashing,LSH)[8]可以很好地保持样本之间的相似性,但是,由于其哈希函数是随机选取而不是通过数据学习得出的,因此,其准确率很低,不能满足现实需求。之后,根据LSH的缺点提出了谱哈希(Spectral Hashing,SpH)[9],但是SpH对于新来的样本,需要通过假设数据分布符合一个超矩形平面,才能得到哈希码。在现实应用中,数据一般不会符合这种假设,因此实用效果差。在SpH的基础上,又提出了迭代量化方法(Iteration Quantization,ITQ)[10]。通过迭代量化的方式,克服了正交投影带来的缺陷。
文中以大数据时代下的图像检索为应用背景,提出一种二进制的哈希自编码模型。通过该模型生成图像紧凑的哈希二进制表示,从而在尽量保证检索准确度的前提下减少检索的时间开销,以达到图像检索在精度和效率方面的良好性能。
1 相关工作
1.1 哈希学习
哈希学习(Learning to hash)起源于数据库领域,并于2007年由Hinton等[11]引入到机器学习领域。随着大数据时代对实时性要求的不断提高,哈希学习逐渐成为机器学习和数据挖掘领域的研究热点。
局部敏感哈希[8]是最为经典的哈希方法之一。局部敏感哈希算法认为至少存在一个投射矩阵可以将相近的数据点映射到相同的桶中。局部敏感哈希使用多个不同的投射矩阵将样本映射到随机的方位。通过这种方式,使得与查询样本相似的样本会以很高的概率映射到相同的桶中。局部敏感哈希方法不仅能保持数据样本之间的相似关系,而且计算速度很快。但是,由于哈希函数是随机选取而不是通过数据学习得出的,因此,其准确率很低,不能满足现实需求。
为了克服LSH的种种缺陷与不足,Weiss提出了谱哈希[9]。SpH第一次定义了什么是好的哈希码,即每个哈希码中0和1应各占50%,不同的哈希码彼此之间应该是正交的。同时,SpH提出得到以上定义的编码与图分割问题等价,而图分割问题是一个NP-hard难题。通过对初始问题进行谱松弛,SpH把问题变成了一个拉普拉斯谱图分解问题。利用主成分分析方法,求得矩阵前k个最小的特征向量,并将其作为哈希学习的映射矩阵。在量化阶段,将映射后的向量用0进行阈值化操作获得最终的二进制码。SpH在平衡和正交限制下只求出了样本的哈希码,并未求得哈希函数。对于新来的样本,需要通过假设数据分布符合一个超矩形平面,才能得到哈希码。在现实应用中,数据一般不会符合这种假设,因此实用效果差。
之后,Gong等提出了迭代量化[10]。在SpH的基础上,采用迭代量化的形式,学习一个旋转矩阵,来修正投影方法和减小量化误差。ITQ分为两个阶段:第一阶段,采用类似SpH的方式学习一个投影矩阵W;第二阶段,采用一种二进制量化的方式,迭代学习一个矩阵R和最后的哈希码B。对于一个新来的样本,将其分别乘以W和R,得到映射后的向量,然后对其进行0阈值化处理得到哈希码。ITQ通过迭代量化的方式,克服了正交投影带来的缺陷,取得了不错的效果。
1.2 极限学习机自编码(Extreme Learning Machine-AutoEncoder,ELM-AE)
Autoencoder[12-13]网络结构包括输入层、隐含层和输出层,其输入层维数与输出层维数D相等。也就是说,Autoencoder通过学习一个恒等函数hω,b(x)≈x,可以实现样本特征的重新表述。那么,当设置隐含层神经元的数目小于D时,即可实现输入层到隐含层的数据降维。为了进一步提高网络的学习特征能力,受人类视觉系统多级信息处理机制启发,可通过增加隐含层,形成深度学习模型,提取样本更加本质的特征。传统的BP算法无法实现深度模型的学习,Autoencoder采用无监督训练方式进行训练学习。
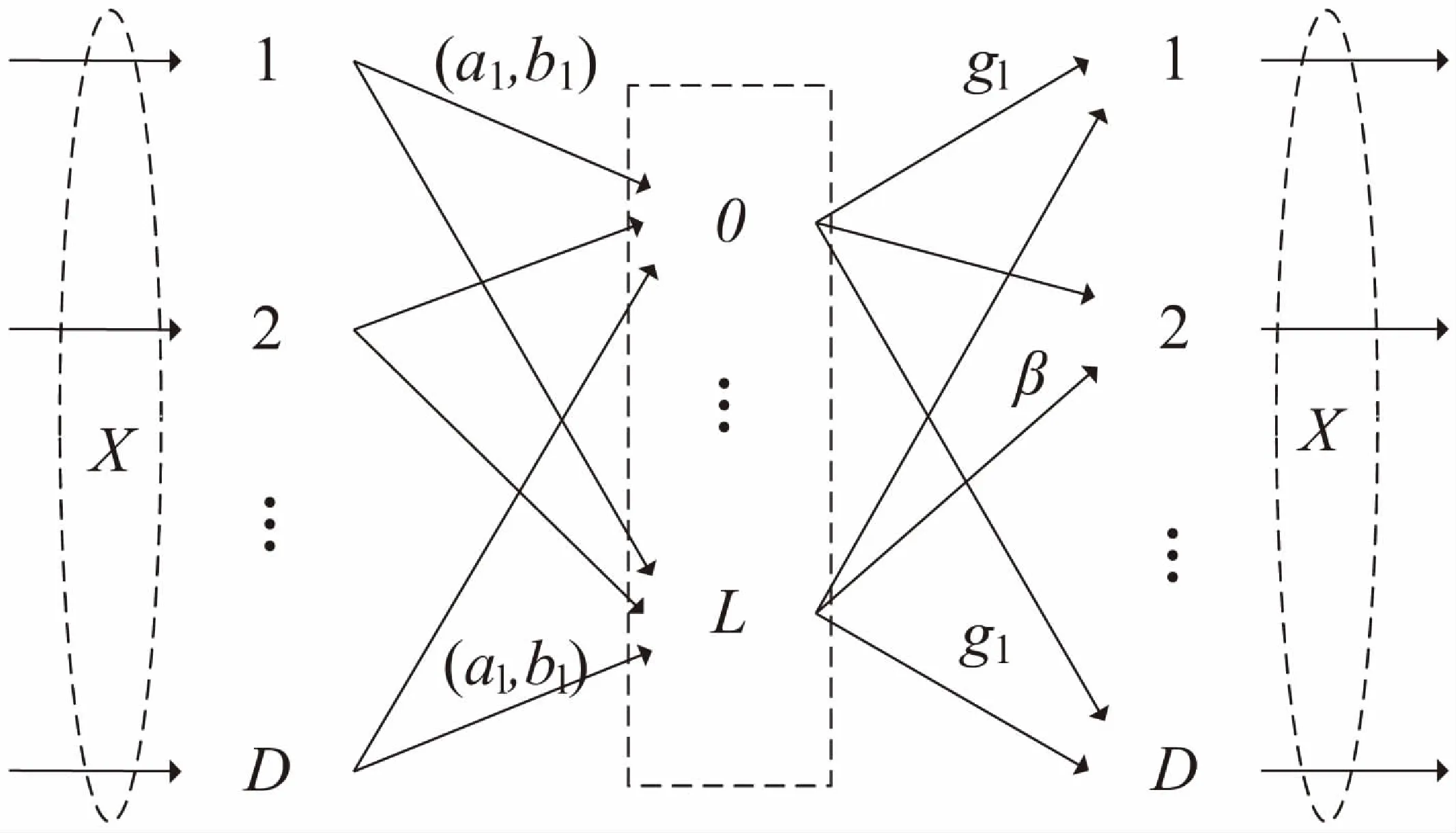
极限学习机自编码[14]具备极限学习机输入参数随机赋值、无需迭代优化等优点,同时具有自编码的功能。与传统极限学习机(Extreme Learning Machine,ELM)[15-16]相同的是,ELM-AE也具有三层网络结构:输入层、隐含层和输出层;不同的是,ELM-AE的目标输出与输入相同(如图1所示)。
设隐含层的节点数为L,输入层与输出层的节点数为D,根据源数据的维度和隐含层的节点数,可以将ELM-AE分为如下三种情况:
(1)压缩:表示特征向量从高维的数据空间映射到低维的特征空间;
(2)稀疏:表示特征向量从较低维的数据空间映射到较高维的特征空间;
(3)等维:表示特征向量从数据空间映射到维度相等的特征空间。
根据ELM理论,输入层与隐含层之间的参数a=[a1,a2,…,aL],b=[b1,b2,…,bL]分别为正交随机权重与偏移,隐含层节点的输出可表示为:
j=g(a·x+b)
aTa=I,bTb=1
当L (1) 其中,J=[j1,j2,…,jn]为隐含层输出矩阵,其神经网络如图1所示。 图1 ELM-AE神经网络 首先,构建一个广义上的自编码模型:定义一个编码器h(x),将真实的向量X∈RD映射到一个真实的码向量Z∈RL(L 然而,这里讨论构建的是一个二进制哈希自编码模型。对于二进制自编码来说,其整个自编码过程可描述为: (1)通过连续地输入特征向量到编码器中,编码器通过哈希函数h(x)将特征向量映射到L位的二进制编码向量Z∈{0,1}L; (2)对二进制编码Z∈{0,1}L进行优化; (3)将优化过的二进制编码向量输入到解码器当中,解码器通过解码函数f(z)将二进制编码向量映射回特征向量,从而实现对特征向量的重建。 (2) 其中,X=(x1,x2,…,xN)为高维的数据集。 称上述自编码模型为二进制非线性哈希自编码。其目标函数可以表示为: (3) 这是通常情况下的最小二乘误差。对于二进制哈希自编码模型,由于其编码器输出的编码为二进制,使得目标函数变得不平滑,而优化这个非平滑函数是很困难的NP计算。 处理高维数据的方式之一是对其进行降维,通过学习以获得低维的模型。这些高维数据通常包含许多冗余,其本质维数往往比原始的数据维数要小得多,因此高维数据的处理问题可以通过相关的降维方法减少一些不太相关的数据,从而降低它的维数,然后用低维数据的处理办法进行处理。 综上所述,称上述模型为基于ELM-AE的二进制非线性哈希自编码模型(简称ELM-AE-Hash)。 (4) 值得注意的是,这里的编码是二进制,使用二次罚函数(或使用增广拉格朗日函数代替),随着μ的逐渐增加,下述目标函数逐渐最小化,最终达到最佳。 (5) 由于在自编码模型中,编码器函数h与解码器函数f成对出现,进而将其看作一个整体,对二进制编码Z和(h,f)实现交替优化,具体可分为两步: (1)固定二进制编码Z,优化(h,f):对于每一个L位的哈希函数h(xn)(试图将X映射到最佳的二进制编码Z)和解码器函数f(zn)(试图将二进制编码Z重建回X),可以获得L+1个独立的问题; (2)固定(h,f),优化二进制编码Z:将N个数据向量分离开来考虑。原数据向量xn的最优编码向量应更好地接近h(xn)的预测值,从而更好地重建数据向量xn。 从上述两个步骤可以看出辅助坐标法的优点:单个步骤是合理且容易解决的;并且它们还表现出显著的并行性。在迭代过程中,允许编码器和解码器不匹配,这是由于编码器的输出不等于解码器的输入,但是它们由Z来协调。随着μ的增加,这种不匹配度是逐渐降低的。算法归结如下: 算法1:ELM-AE-Hash算法。 输入:XD×N=(x1,x2,…,xN); 初始化:(使用ELM-AE对X进行初始优化) ZL×N=(z1,z2,…,zN)∈{0,1}LN Step1: forμ=0<μ1<…<μ forl=1,2,…,L 利用SVM训练hl中的参数,并得到二进制编码Z 解码器f(Z)将二进制编码Z重建回X' Step 2: forn=1,2,…,N 终止:Z不再改变且Z=h(X') 返回:h,Z=h(X') 其中,由于模型中的二进制特性,这里的μ值,不需要趋近无限大,算法可以收敛到一个局部最小的有限μ值。 本次实验通过在映射空间上对汉明距离使用KNN[18-19]算法,设定合适的近邻值,得到最佳的准确率。使用的三个基准数据集均为常用的图像检索的数据集,分别为: (1)CIFAR[20]包含60 000个32*32的彩色图像,共有10类(如图2所示)。实验中忽略其标签,并使用N=50 000个图像作为训练集,10 000个图像作为测试集。并从每个图像中提取D=320维的GIST特征[21]; (2)NUSWIDE[22]包含N=269 648个高分辨率的彩色图像,使用161 789个作为训练数据集,107 859个图像作为测试集,并从每个图像中提取D=128维的小波特征[21]; (3)SIFT-1M[23]包含N=1 000 000个高分辨率的彩色图像训练数据集和10 000个测试图像,每一张图像通过D=128维SIFT特征表示。 图2 CIFAR数据集 对于二进制编码Z的位数L,最佳的位数应该在8~32之间,对此区间内的自编码模型进行实验,其准确率如图3所示。 图3 不同二进制位数下ELM-AE-Hash算法精度 由图3可以看出,当L越大时,准确率越高,图像检索越为精确。但是,随着二进制编码位数的增大,在图像存储方面会消耗更多的存储空间,所以这里的二进制位数不易过大。文中的所有实验均设定L=16,在此基础上对算法进行各个场景下的实验评估。 通过两个具体的实验对模型从不同的角度进行了全面分析,验证算法的性能。 如上述提到的,在此哈希自编码模型中,编码器函数(哈希函数)使用非线性的sigmoid函数(h(X)=S(Wx))。为了说明使用非线性哈希函数的必要性,构建一个对比模型,将非线性哈希函数h更换为线性函数h(X)=σ(Wx)(其中σ(t)为阶跃函数,当t≥0时,σ(t)=1;当t<0时,σ(t)=0)。对这两个模型分别使用KNN,其精度变化趋势如图4所示。 由图4可见,设置KNN算法中的近邻个数,k={50,60,70,80,90,100}。分别对不同k值下非线性模型和线性模型进行精度的计算。可以看出,随着k值的增加,不同激励函数下的哈希模型准确率均呈下降趋势,这是由于KNN算法本身的特性[24]所决定的。但是,对于每一个不同的近邻值k都有:拥有非线性激励函数的模型精确度高于线性激励函数模型,并且优势明显。同时,由于线性函数本身所固有的局限性,采用非线性的编码器函数h(x)和相应的解码器函数f(z),使得非线性的自编码模型适用于更多情况下的数据样本集。 图4 不同激励函数下ELM-AE-Hash的精度 实验中,将ELM-AE-Hash算法与其他经典图像检索算法进行性能比较。比较算法包括:迭代优化(ITQ)、主成分分析(PCA)[25]以及二进制因子分析法(BFA)[26]。性能比较指标包括准确率(%)和运行时间(s)。图5和图6分别展示了ELM-AE-Hash与其他各算法的准确率和运行时间对比。 图5 ELM-AE-Hash算法与其他算法的精度对比 图6 ELM-AE-Hash算法与其他算法的运行时间对比 从图5可以看出,在准确率方面,随着近邻值k的增加,各个算法的准确率均呈下降趋势;但是,在每一个k值下,ELM-AE-Hash模型的准确率均高于其他算法,并且优势较为显著。这是由于ELM-AE-Hash模型采用了MAC来实现算法的优化,遵循了二进制约束,而ITQ和PCA算法并未考虑遵循二进制约束;并且,使用ELM-AE对样本数据集进行优化,降低了数据样本集的冗余,从而全面地提高了模型的精确度。 在时间运行方面,固定一切可变因素,采用相同配置的计算机、同版本的编译软件MATLAB R2014a,以及相同的数据集,连续收集10次各个算法的运行时间。从图6可以看出:ELM-AE-Hash模型的运行时间在37~46 s之间,平均值为42.3 s;PCA算法的运行时间在43~56 s之间,平均值为48.8 s;ITQ算法的运行时间在45~55 s之间,平均值为50.8 s;BFA模型的运行时间在47~63 s之间,平均值为52.9 s。由此可知,文中所设计实现的哈希模型在运行时间方面优于其他几种图像检索算法。 文中基于ELM-AE提出了一种新型的非线性二进制哈希自编码检索模型。通过ELM-AE对图像样本进行优化,降低数据冗余,提升图像检索模型的效率;其次,通过二进制哈希自编码实现高维图像数据向低维二进制空间的映射和重表,提升了图像检索的精度;同时,使用非线性哈希函数解决了线性函数在处理复杂数据时的局限性的问题。实验评估表明,对于大规模数据,提出的ELM-AE-Hash模型不仅有较高的图像检索效率,同时具有较高的检索精度。 [1] 严灵毓.面向图像检索的感知哈希算法研究[D].武汉:华中科技大学,2014. [2] Wang Q,Zhang D,Si L.Semantic hashing using tags and topic modeling[C]//International ACM SIGIR conference on research and development in information retrieval.[s.l.]:ACM,2013:213-222. [3] Wang Q,Si L,Zhang Z,et al.Active hashing with joint data example and tag selection[C]//International ACM SIGIR conference on research & development in information retrieval.[s.l.]:ACM,2014:405-414. [4] Kong W. Double-bit quantization for hashing[C]//AAAI conference on artificial intelligence.[s.l.]:[s.n.],2004:137-138. [5] Lin G,Shen C,Suter D,et al.A general two-step approach to learning-based hashing[C]//IEEE international conference on computer vision.[s.l.]:IEEE,2013:2552-2559. [6] 杨 垚.面向多示例数据检索的哈希方法研究[D].济南:山东大学,2016. [7] 赵玉鑫.多媒体感知哈希算法及应用研究[D].南京:南京理工大学,2009. [8] Gionis A,Indyk P,Motwani R.Similarity search in high dimensions via hashing[C]//International conference on very large data bases.[s.l.]:Morgan Kaufmann Publishers Inc.,2000:518-529. [9] Weiss Y,Torralba A,Fergus R.Spectral hashing[C]//Conference on neural information processing systems.Vancouver,British Columbia,Canada:[s.n.],2008:1753-1760. [10] Gong Y,Lazebnik S,Gordo A,et al.Iterative quantization:a procrustean approach to learning binary codes for large-scale image retrieval[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2013,35(12):2916-2929. [11] Salakhutdinov R,Hinton G.Semantic hashing[J].International Journal of Approximate Reasoning,2009,50(7):969-978. [12] Hinton G E,Osindero S,Yw T.A fast learning algorithm for deep belief nets[J].Neural Computation,2006,18(7):1527-1554. [13] 曲建岭,杜辰飞,邸亚洲,等.深度自动编码器的研究与展望[J].计算机与现代化,2014(8):128-134. [14] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006,70(1-3):489-501. [15] 邓万宇,郑庆华,陈 琳,等.神经网络极速学习方法研究[J].计算机学报,2010,33(2):279-287. [16] 邓万宇,杨丽霞.基于Spark的OS-ELM并行化算法[J].西安邮电大学学报,2016,21(2):101-104. [17] Carreira-Perpián M A,Wang W.Distributed optimization of deeply nested systems[C]//AISTATS.[s.l.]:[s.n.],2014. [18] Hastie T,Tibshirani R.Discriminant adaptive nearest neighbor classification[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,1996,18(6):607-616. [19] Yang Y,Pedersen J O.A comparative study on feature selection in text categorization[C]//Fourteenth international conference on machine learning.[s.l.]:Morgan Kaufmann Publishers Inc.,1997:412-420. [20] Krizhevsky A.Learning multiple layers of features from tiny images[D].Toronto:University of Toronto,2009. [21] Oliva A,Torralba A.Modeling the shape of the scene:a holistic representation of the spatial envelope[J].International Journal of Computer Vision,2001,42(3):145-175. [22] Jeyakumar V,Rubinov A M,Wu Z Y.Non-convex quadratic minimization problems with quadratic constraints:global optimality conditions[J].Mathematical Programming,2007,110(3):521-541. [23] Jegou H,Douze M,Schmid C.Product quantization for nearest neighbor search[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(1):117-128. [24] 耿丽娟,李星毅.用于大数据分类的KNN算法研究[J].计算机应用研究,2014,31(5):1342-1344. [25] Price A L,Patterson N J,Plenge R M,et al.Principal components analysis corrects for stratification in genome-wide association studies[J].Nature Genetics,2006,38(8):904. [26] Carreira-Perpinan M A,Raziperchikolaei R.Hashing with binary autoencoders[C]//IEEE conference on computer vision and pattern recognition.[s.l.]:IEEE,2015:557-566. ABinaryNonlinearHashingAlgorithmwithELMAuto-encoders DENG Wan-yu,ZHANG Qian,QU Yu-tao (School of Computer,Xi’an University of Posts and Telecommunications,Xi’an 710000,China) The field of Internet applications is so expandable because of the development of mobile Internet,social network and e-commerce in the data information age of 21 century that the various types of data are in explosive growth,which make the traditional data analysis ineffective.In order to effectively solve the problem of retrieval of image with large scale and meet the application requirements of large scale image database,a binary nonlinear hashing algorithm based on Extreme Learning Machine Auto-Encoders (ELM-AE) is proposed.It optimizes the data sample by ELM-AE and raises the efficiency of image retrieval.Through binary hashing to implement the mapping from high-dimensional image data to low-dimensional binary space,the retrieval accuracy and efficiency are improved.In addition,nonlinear retrieval problem is solved by nonlinear activation function.The experimental results show that the proposed algorithm achieves good retrieval efficiency and accuracy with good performance in operation time and other aspects. hashing learning;auto-encoders;extreme learning machine;image retrieval;machine learning TP399;TP391.4 A 1673-629X(2017)12-0061-06 10.3969/j.issn.1673-629X.2017.12.014 2016-12-15 2017-04-20 < class="emphasis_bold">网络出版时间 时间:2017-08-01 国家自然科学基金资助项目(61572399);陕西省青年科技新星资助项目(2013KJXX-29) 邓万宇(1979-),男,博士,教授,研究方向为数据挖掘、机器学习;张 倩(1992-),女,硕士,研究方向为数据挖掘、机器学习。 http://kns.cnki.net/kcms/detail/61.1450.TP.20170801.1556.062.html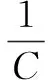
2 基于ELM-AE的二进制非线性哈希算法及其优化
2.1 基于ELM-AE的二进制非线性哈希算法模型构建
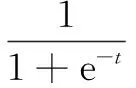

2.2 模型优化

3 实验结果与分析

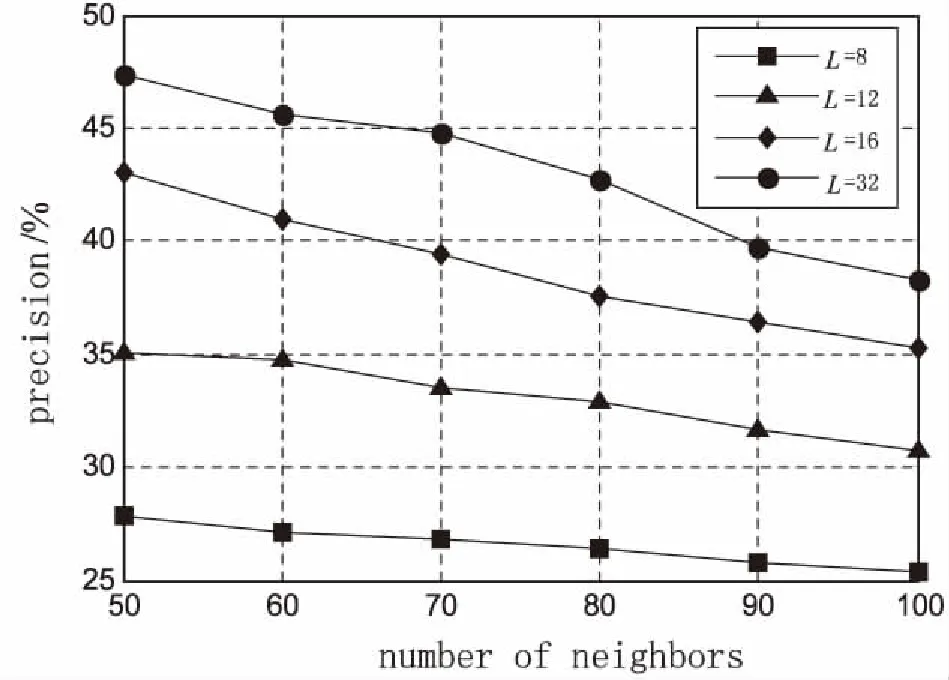
3.1 激励函数对模型性能的影响
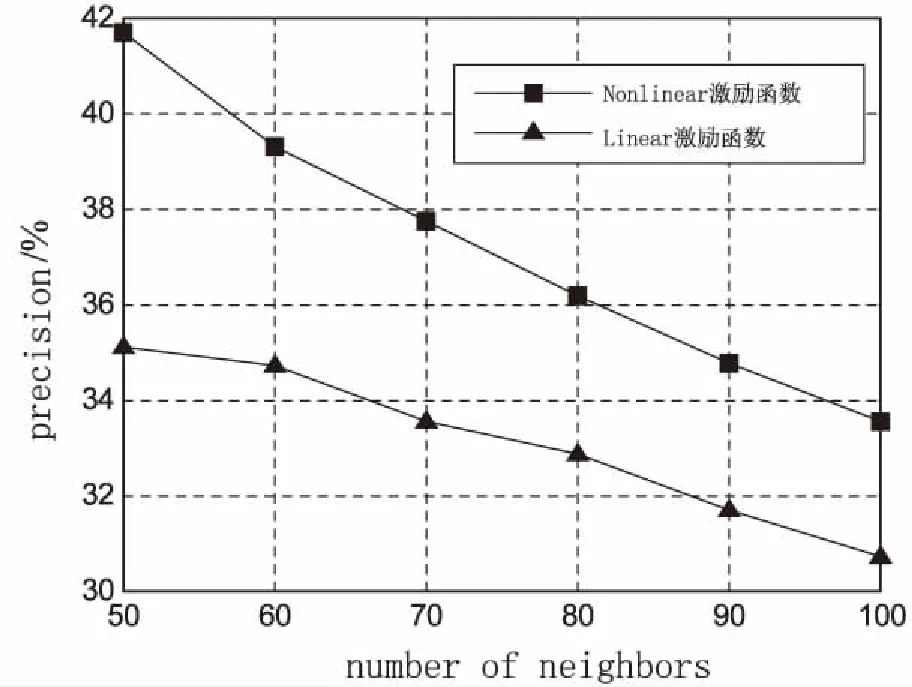
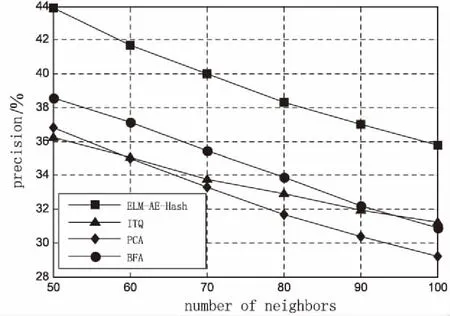
3.2 ELM-AE-Hash算法与其他算法的性能比较
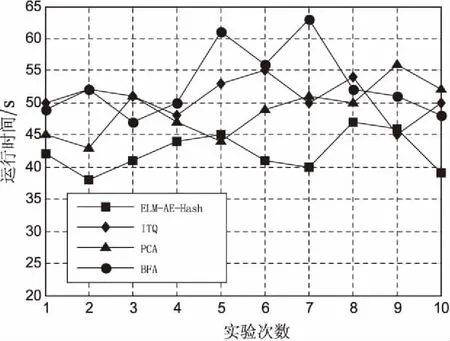
4 结束语

