复杂建筑物尖端雷击概率的模拟研究
王梦寒,侯文豪,张其林,申 元
(1.南京信息工程大学气象灾害教育部重点实验室/气候与环境变化国际合作联合实验室/气象灾害预报预警与评估协同创新中心/中国气象局气溶胶与云降水重点开放实验室,南京210044;2.云南电网有限责任公司电力科学研究院,昆明650217)
复杂建筑物尖端雷击概率的模拟研究
王梦寒1,侯文豪1,张其林1,申 元2
(1.南京信息工程大学气象灾害教育部重点实验室/气候与环境变化国际合作联合实验室/气象灾害预报预警与评估协同创新中心/中国气象局气溶胶与云降水重点开放实验室,南京210044;2.云南电网有限责任公司电力科学研究院,昆明650217)
在地闪连接过程中,正极性连接先导的始发和传播是决定建筑物是否遭受雷击的关键因素之一。但广泛应用于确定建筑物雷击点的滚球法并没有考虑上行正极性先导的始发过程。因此,基于充分考虑了闪电先导及其连接过程的物理先导模型,选取不同形状的建筑物对建筑物的雷击点概率问题进行了研究,通过估计复杂建筑物拐角等尖端处始发稳定的上行先导所必需的背景电场来确定建筑物雷击点的概率。结果表明:下行先导接近地面建筑物时上行先导首先起始的位置成为雷击点的概率比较高;除此之外,判断建筑物雷击点时不仅仅依赖于滚球法中强调的雷击电流的大小,建筑物的几何形状及周围因素对雷击点的估测也是不可忽视的。基于本文的研究结果可为建筑物的雷击状况的分析和今后解决复杂建筑物的雷电防护等实际应用问题提供了较好的依据。
雷击点;上行正极性先导;复杂建筑物;雷电防护
0 引言
闪电是发生于大气中的一种长距离、大电流、强电磁辐射瞬时放电事件[1],常常引起各种严重的灾害,特别是电子电气设备的大量采用,雷电灾害越来越严重,影响也越来越大[2-3]。所以采用可靠的雷电防护措施可以有效的减少雷电灾害。目前广泛采用的电气几何模型[4-6]比较简化的认为,假设当一定电流强度下的下行梯级先导头部与闪击点之间达到临界距离时,便认为在该处发生闪击。即闪击点仅由雷电流幅值来决定,没有考虑建筑高度或是几何尺寸对其的影响,也没有考虑上行先导的始发过程,所以该模型过度的简化了闪电放电过程中的物理过程,且对高层建筑物的雷击状况分析尚未提出有效的计算方法,难以满足日益迫切的防雷保护要求。
由于滚球法的局限性,Eriksson将电气几何模型进行了改进,提出了收集体积法(collection volume method,CVM),并提出该方法可以应用到建筑物上[7]。收集体积被定义为由闪击距离和由下行先导与上行先导的速度比决定的边界所决定的区域[8]。当下行先导进入到收集体积区域时建筑物易遭受雷击。虽然收集体积法被用于建筑物闪击距离的计算[9],但该方法的有效性仍受着质疑[10-11]。
随着对闪电物理过程认识的不断深入,通过闪电先导及其连接过程来研究雷电防护问题已成为一种重要的方法。在负极性雷电地闪过程中,建筑物拐角等尖端处的正极性迎面先导起始过程是决定其保护范围的关键。因此,迎面先导起始的研究对建筑物的雷电防护的研究十分有益。
Dellera学者根据Carrara[12]于正极性放电试验中得到的临界半径的概念,提出了临界半径法(critical corona radius,CCR)[13-14],该方法用于作为避雷针和输电线路的正极性迎面先导的起始判据,但是否可以适用于建筑物目前尚不清楚;Rizk将其在长间隙放电击穿特性计算模型中提出的连续先导起始电压公式作为迎面先导起始判据[15-17],但其适用范围为电极曲率半径小于临界电晕半径的目的物;Petrov和Waters提出的临界长度法认为在迎面先导前方流注区的电场强度大于正极性流注的平均场强500 kV/m且流注长度大于0.7 m时迎面先导起始[9-18]。但该临界长度方法与CCR和Rizk的感应电压法均来自于对正极性放电试验宏观特性的总结,故均受限于实验条件。因此,以上三种判据多来自于对长间隙放电试验结果的分析和总结,缺少对放电物理机理的描述,能否直接用于判断建筑物正极性迎面先导的起始还有待论证。
Gallimberti等学者分析了正极性流注-先导发展过程中产生的空间电荷与间隙电位畸变的关系,建立了包括初始电晕起始、流注发展、先导起始、流注-先导系统发展和最后跃变在内的正极性先导发展的物理模型[19-20]。Becerra和Cooray在Gallimberti工作的基础上优化了流注区空间电荷分布,建立了考虑空间电荷影响的正极性上行先导起始和发展的物理模型(self-consistent leader inception and propagation model,SLIM),该模型得出正极性先导起始所需要的临界电荷量约为1 μC[21],随后,Becerra和Cooray在其正极性迎面先导起始和发展模型中,均采用1 μC作为迎面先导起始的判据[22-24]。该模型可较好的应用于地面建筑物、电力杆塔及传输线的连接过程,并且通过与观测资料进行对比也验证了该模型的可靠性。
综上所述物理先导模型充分考虑了闪电放电的物理过程,考虑了正极性先导的起始和连接过程,能够更加真实合理的描述雷击过程,笔者基于物理先导模型对复杂建筑物尖端处的雷击概率进行研究与分析,旨在为建筑物的雷电防护设计中提供较好的理论依据。
1 物理先导模型
1.1 稳定的上行先导始发条件
闪电发生于云内局部强电场区域,并逐步演变成可以在地电场区域中持续传输的先导。梯级先导是地闪放电的始发阶段,当梯级先导头部接近地面时,地面的突出物体上会产生上行先导,二者相连接的过程即为连接过程。由于先导间存在着巨大的电位差,在连接后会发生剧烈的放电过程。
为了确定最可能的雷击点,对建筑物的所有拐角,边缘和平坦表面的先导始发情况进行估测是必要的。为了克服已有的先导始发判据不能应用于复杂建筑物的限制,本文采用的是Becerra与Cooray[24]提出的先导始发模型。该始发模型模拟了由建筑物始发的的上行先导的传播过程,其中包括对称和非对称等任何形状的建筑物。该模型有以下假设:当背景电场足够大以保证先导可以持续向前发展到最初数米时,则一个稳定的自持传播的上行先导始发;当上行先导始发时由下行先导生产的电场没有大幅变化,通过考虑这种静态情况,先导始发模型复杂的动态情况也就随之避免了。因此,为了判断在下行先导头部处于给定高度情况下稳定先导是否起始,建筑物尖端处上行先导发展过程模型见图1。
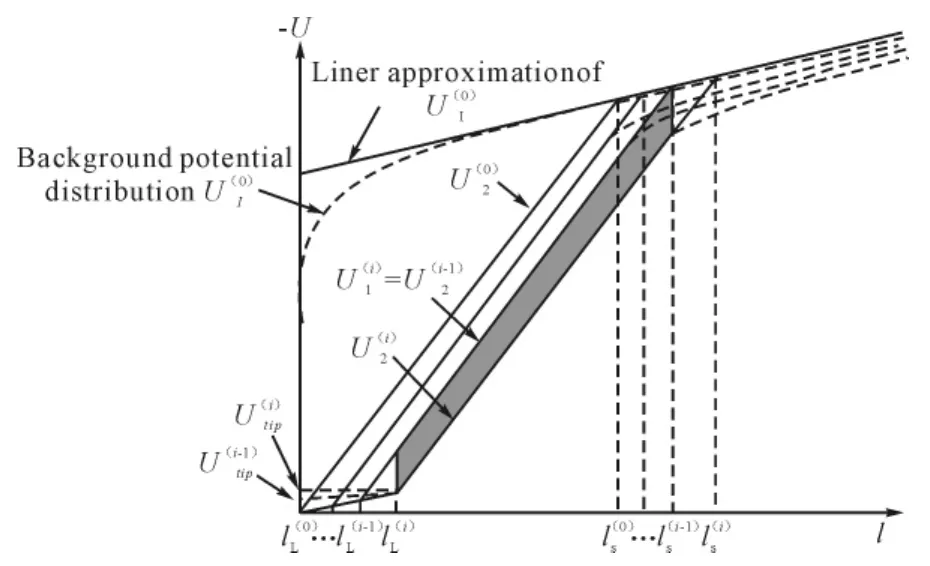
图1 建筑物尖端处上行先导发展过程模型Fig.1 Buildings at the tip upward leader development process model

式中,E1即为线性方程的斜率,如图1所示为与纵坐标的截距,l为下行先导头部与建筑物尖端的距离。

式中,Estr为流注区域的电位梯度,也可以视为常数。

则二次电晕区域的电荷量 ΔQ(0)可以由 KQ和(1)式及(2)式表征的直线间区域面积的乘积得到:
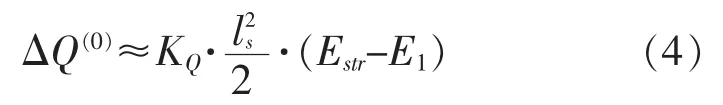
当ΔQ>1μC时,视为不稳定先导起始,并向前步进迭代,且假定。由图1可见,在第i步迭代中,电势分布可以表示为


式中,E∞为最终稳定先导的电位梯度;x0为一个常数,是上行正先导的发展速V和时间常数θ的乘积。

以及先导头部产生的电晕电荷量ΔQ(i)近似由下式计算

式中括号内的部分为图1中阴影部分的面积。设单位长度的上行先导通道电荷量为qL,则第i+1步先导的长度可由第i步先导长度加上所得,可表示为

由此,经过若干步迭代,当lL达到一个临界长度Lmax(2m)时,判定稳定连续的上向先导起始;而迭代若干步后lL开始减小,则上行先导不起始。该判据充分考虑了先导放电过程,更符合上行先导产生和发展的微观物理机制,精确度更高。判据中使用到的常量[20]及参数如表1所示。

表1 常量及参数Table 1 Constant and parameters
1.2 静电场计算
静电场计算也是一个重要方面,同时,解三维的泊松方程需要大量的计算时间和内存。笔者使用的是一种基于商业软件COMSOL的有限元法(FEM)来计算建筑物每个拐角等尖端处的电位分布[25],如图1所示。由于网格点数量的限制,只考虑了有限的研究区域,忽略了阶梯先导的上部[26]。笔者选取的研究区域为1 200 m×1 200 m×600 m,将梯级先导通道设置为垂直于地面方向发展,其内部电荷分布如等式(1)所示。进一步分析表明,当下行先导的上部被忽略时所计算的电位分布没有明显影响,这是因为最大电荷密度出现在其通道头部[26],因此,靠近地面的电场主要与下行先导的下部有关。假定地面上方600 m范围内的背景电场为一恒定值10 kV/m,这里的背景电场主要表征雷暴云中分布的空间电荷在其下方近地面附近产生的影响,虽然实际电场探空结果表明,雷暴云下电场强度随着高度增加而增强,但通过对背景电场对梯级长度的影响分析表明这一影响很小,这可能是目前关于先导连接过程模拟中多采用恒定背景电场近似假设的原因[27-29]。上表面边界的电位由背景电场的场值与研究区域的高度共同确定。由于模拟区域相对于雷暴云的空间尺度很小,而相对于先导直径又很大,在模型中背景电场的假设表示为:上边界具有恒定电位,地面电位为零,此外,研究区域的侧面是切向电场为零的开放边界,见图2。

图2 研究区域与细化网格Fig.2 An analysis volume and mesh subdivision
雷电下行先导是地面附近空间电场的主要激励源,因此,其发展通道内电荷量的大小及分布形式对于模拟结果具有非常大的影响。采用Cooray[21]等学者推荐的下行先导通道电荷分布与雷电流幅值关系模型,即下行先导通道电荷产生的电场可由下行先导通道位置及其电荷密度分布特征计算得到,通道内的电荷在先导头部随高度呈指数衰减,而在其他区域则呈线性衰减趋势,其电荷分布为

式中,zo为下行先导头部距离地面的高度(m),L 为梯级先导通道的长度(m),ρ(ζ)为电荷密度(C/m),ζ为先导通道中某位置距先导头部的距离(ζ=0对应于先导的头部),Ip=30 kA,为雷电流幅值,a0=1.48×10-5,a=4.86×10-5,b=3.91×10R,c=0.52,d=3.73×10-3。
2 建筑物尖端雷击概率的研究
笔者将对建筑物正上方垂直10m的电势进行计算,同时将可以使稳定连续的上行正先导始发的最小背景电场定义为稳定电场。通过对建筑物各尖端处稳定电场的计算得到稳定电场最小处便是最易遭受到雷击的位置,则假设该处被雷击的概率接近1(或100%)。建筑物其他位置遭受雷击的概率可以通过两位置的稳定电场的比值进行确定,假设在建筑物某尖端处X被闪电击中的概率为100%,那么建筑物其他位置如Y的雷击概率可以通过EX/EY得到。按照此定义可知,被闪电击中概率为100%位置处更容易使稳定的正先导始发。
笔者通过选取不同的建筑物对雷击概率问题进行了分析,图3选取的是两个相同高度的建筑物,尺寸均为30 m×70 m×100 m,两建筑物相距30 m,标记建筑物可能受到雷击的点分别为 A、B、C、D、E、F、G、H,下行先导的位置处于建筑物A点的正上方。

图3 两个相同高度的建筑物,尺寸均为30 m×70 m×100 mFig.3 Two buildings with the same height,dimensions are both 30 m×70 m×100 m
经过计算可以得到每个可能雷击点的稳定电场以及各雷击点受到的雷击概率,如表2所示,其中最容易受到雷击的雷击点的概率记为100%。可以看到,处于下行先导正下方的A点的电场最小,即A点最容易使稳定的上行正先导始发,最容易遭受雷击。同样处于两建筑物外围的B、G、H受到雷击的概率也比较大,均在93%以上。理论上由于建筑物的对称性,其他几点所受到的雷击概率应该是相似的,而C、D、E、F几点由于建筑物相距的比较近受到雷击的概率相对较小,这是由于建筑物外围的拐角对内侧的拐角起到了相对保护的作用。由此也可以发现建筑物的拐角是比较容易遭到雷击的,引起的电场畸变比较大,所以在对建筑物进行雷电防护设计时,对建筑物拐角的防护也是不容忽视的。
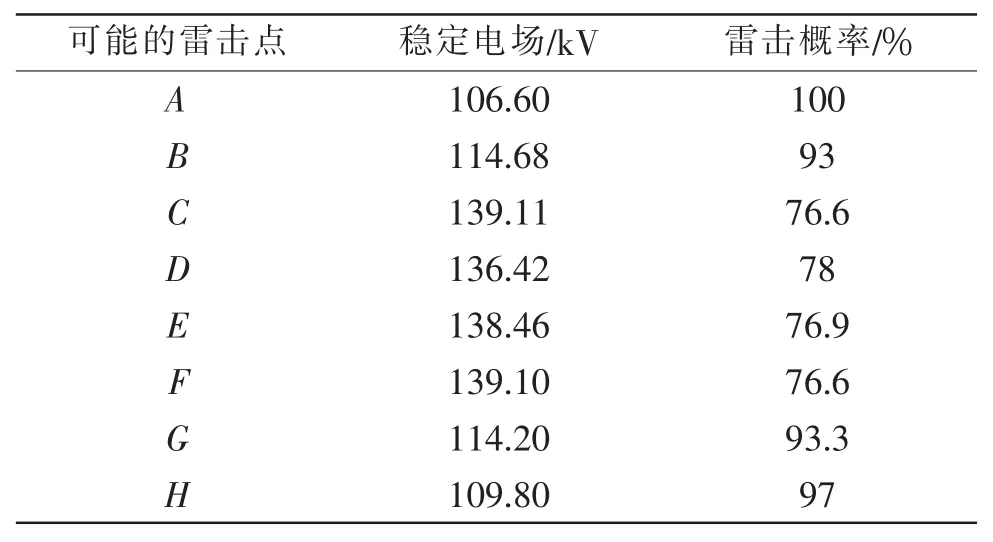
表2 尺寸均为30 m×70 m×100 m的两建筑物拐角的雷击点概率Table 2 The probability of lightning strike points on the coners of two buildings with dimensions are both 30 m×70 m×100 m
图4选取的是两个不同高度的建筑物,尺寸分别为 50 m×50 m×70 m 和 30 m×70 m×110 m,两建筑物间的距离仍为30 m,下行先导仍处于建筑物A点的正上方。计算结果如表3所示。

图4 两个不同高度的建筑物,尺寸分别为50 m×50 m×70 m和 30 m×70 m×110 mFig.4 Two different height buildings,dimensions are 50 m×50 m×70 m and 30 m×70 m×110 m

表3 尺寸分别为50 m×50 m×70 m 和30 m×70 m×110 m两建筑物拐角的雷击点概率Table 3 The probability of lightning strike points on the coners of two different height buildings with dimensions are 50 m×50 m×70 m and30 m×70 m×110 m
110 m高的建筑物各尖端的稳定电场均比70 m高的建筑物各尖端的稳定电场小,即高度越高的建筑物更容易遭受雷击,其中110 m高的建筑物的A点是最容易遭受雷击的,B、C、D三个拐角的雷击概率均在90%以上。单独就70 m高的建筑物而言,如果G、H两处的先导始发电场没有归一化到尖端A处的最小稳定电场,那么拐角G、H处的雷击概率是接近于100%的。而相对于A点的最小稳定电场G、H两点的雷击概率接近75%。但仍然可以看出B、C的保护空间不足以保护70 m高建筑物的外围拐角G和H两点,另一方面,外围的G、H比内侧的E、F两点的雷击概率要高的多,原因在于E、F两点靠近110 m高的建筑物,110 m高的建筑物对E、F两点有屏蔽影响,起到了保护性的作用。
图5选取了两个尺寸分别为30 m×30 m×60 m和50 m×50 m×100 m的建筑物进行雷击概率的研究,且在100 m高的建筑物上有一个突出的尖端,记为T。计算结果如表4所示。
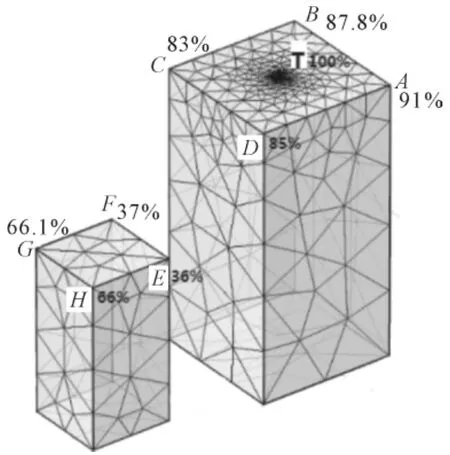
图5 考虑尖端的两不同高度的建筑物,尺寸分别为30 m×30 m×60 m 和 50 m×50 m×100 mFig.5 Two different height buildings with considering tip,dimensions are 30 m×30 m×60 m and 50 m×50 m×100 m

表4 尺寸分别为30 m×30 m×60 m和50 m×50 m×100 m的两建筑物尖端及拐角的雷击点概率Table 4 The probability of lightning strike points on the tip and coners of two different height buildings with dimensions are 30 m×30 m×60 m and 50 m×50 m×100 m
尖端T最易始发上行连接先导,即最易遭受到雷击(概率为100%),然而可以看出建筑物外围的A、B、C、D四点有着较高的先导始发概率(分别为91%、87.8%、83%、85%),说明尖端T的保护范围并不足以保护A、B、C、D等拐角处。如果在T的位置放置一接闪杆来代替尖端T,那么就需要增加接闪杆的高度才可以对100 m高的建筑物各处起到保护作用。另一方面,100 m高的建筑物的A、B、C、D四点的雷击概率高于60 m高的建筑物的各个拐角,由于60 m建筑物周围存在着100 m高的建筑物,故四个拐角并不容易始发上行连接先导,即对60 m高的建筑物起到了保护作用。也可以看出,100 m高的建筑物各个拐角虽没有尖端T更易遭受雷击,却与尖端T存在着竞争的关系,这说明了建筑物拐角在雷电防护设计中仍然是值得考虑的问题。
除此之外,建筑物周围的因素也会对雷击的概率造成一定的影响,本文又通过在与100 m高的建筑物相距100 m处增加了一个30 m×70 m×110 m的建筑物,如图6所示,通过计算,虽然相隔的距离有些远,但还是对计算结果造成了一定的影响,就A点而言,雷击概率由91%变为了84%,降低了该建筑物的雷击概率,故地面建筑物始发稳定的上行先导不仅仅依赖于由下行先导产生的背景电场(与类电流峰值相关),建筑物的形状以及周围的建筑物也是影响建筑物雷击概率不可忽略的问题。同时也对滚球法(只考虑了雷电流峰值)直接应用于复杂建筑物保护范围的准确性提出了更高的要求。

图6 考虑尖端和周围建筑的两不同高度的建筑物Fig.6 Two different height buildings with considering tip and surrounding building
3 结语
基于物理先导模型,通过估计复杂建筑物拐角等尖端处始发稳定的上行先导所必需的背景电场来研究建筑物雷击点的问题。结果表明:建筑物上先导始发的电场值越小的位置越容易遭受雷击,即下行先导接近地面建筑物时上行先导首先起始的位置成为雷击点的概率比较高;除此之外,建筑物的几何形状(主要是高度)及周围因素对雷击点的估测也是由影响的。因此,判断建筑物雷击点时不仅仅依赖于滚球法中强调的雷击电流的大小,建筑物的几何形状尤其是高度以及周围的建筑物等因素也是需要考虑的。以上结果可以帮助雷电防护设计者来确定建筑物雷击防护的最优位置,这为建筑物的雷击状况的分析和今后解决建筑物的防雷保护等实际应用问题提供了较好的依据。
[1]任恒,陈剑云,罗冰波.基于两种国标对雷击建筑物附近引起内部系统故障概率的研究[J].电瓷避雷器,2015(6):103-106.REN Heng,CHEN Jianyun,LUO Bingbo.Study on Building Internal System Failure Probability Caused by Nearby Lightning Strikes Based on Two National Standard[J].Insulators and Surge Arresters,2015(6):103-106.
[2]任晓毓,张义军,吕伟涛,等.雷击建筑物的先导连接过程模拟[J].应用气象学报,2010,21(4):450-457.REN Xiaoyu,ZHANG Yijun,Lü Weitao.Simulation of Lightning Leaders and Connection Process with Structures[J].Journal of Applied Meteorological Science,2010,4:450-457.
[3]张义军,周秀骥.雷电研究的回顾和进展[J].应用气象学报,2006,17(6):829-834.ZHANG Yijun,ZHOU Xiuji.Review and Progress of Lightning Research[J].Journal of Applied Meteorological Science,2006,17(6):829-834.
[4]赵斌财,周浩,钟一俊,等.输电线路雷电绕击研究方法浅议[J].电瓷避雷器,2008(1):29-34.ZHAO Bincai,ZHOU Hao,ZHONG Yijun.Approaching to Rotated Lightning Strike on Transmission Line[J].Insulators and Surge Arresters,2008(1):29-34.
[5]ARMSTRONG H R,WHITEHEAD E R.Field and Analytical Studies of Transmission Line Shielding[J].IEEE Transactions on Power Apparatus&Systems,1968,pas-87(1):270-281.
[6]MOORE C B,AULICH G D,RISON W.Measurements of Lightning Rod Responses to Nearby Strikes[J].Geophysical Research Letters,2000,27(10):1487-1490.
[7]HARTONO Z A,ROBIAH I,DARVENIZA M.A Database of Llightning Damage Caused by Bypasses of Air Terminals on Buildings in Kuala Lumpur,Malaysia[C]//International Symposium on Lightning Protection.University of Sao Paulo,2010:211-216.
[8]ALESSANDRO F D’,GUMLEY JR.A Collection Volume Method for the Placement of Air Terminals for the Protection of Structures Against Lightning[J].Journal of Electro-statics,2001,50(4):279-302.
[9]ERIKSSON A J,An Improved Electro-geometric Model for Transmission Line Shielding Analysis[J].IEEE Transactions on Power Delivery.1987,PWDR-2:871-886.
[10]PETROV N I,WATERS R T.Determination of the Striking Distance of Lightning to Earthed Structures[J].Proceedings of the Royal Society A,1995,450(1940):589-601.
[11]MOUSA A M.Proposed Research on the Collection Volume Method/Field Intensification Method for the Placement of Air terminals on Structures[J],Power Engineering Society General Meeting,vol.1,2003,pp.301-305.
[12]CARRARA G,THIONE L.Switching Surge Strength of Large Air Gaps:A Physical Approach[J].IEEE Transactions on Power Apparatus and Systems,1976,95(2):512-524.
[13]DELLERA L,GARBAGNATI E.Lightning Stroke Simulation by Means of the Leader Progression Model,PartⅠ:Description of the Model and Evaluation of Exposure of Free -standing Structures[J].IEEE Transactions on Power Delivery,1990,5(4):2009-2022.
[14]DELLERA L,GARBAGNATI E.Lightning Stroke Simulation by Means of the Leader Progression model,partⅡ :Exposure and Shielding Failure Evaluation of Overhead Lines with Assessment of Application Graphs[J].IEEE Transactionson Power Delivery,1990,5(4):2023-2029.
[15]RIZK F A M.Modeling of Transmission Line Exposure to Direct Lightning Strokes[J].IEEE Transactions on Power Delivery,1990,5(4):1983-1997
[16]RIZK F A M.Switching Impulse Strength of Air Insulation:Leader Inception Criterion[J].IEEE Transactions on Power Delivery,1989,4(4):2187-2195.
[17]RIZK F A M.A Model for Switching Impulse Leader Inception and Breakdown of Long Air-gaps[J].IEEE Transactions on Power Delivery,1989,4(1):596-606.
[18]PETROV N I,ALESSANDRO F D.Theoretical Analysis of the Processes Involved in Lightning Attachment to Earthed Structures[J].Journal of Physics D:Applied Physics,2002(35):1788-1795.
[19]GALLIMBERTI I.The Mechanism of Long Spark Formation[J].Le Journal De Physique Colloques,1979,40(C7):193-250.
[20]BONDIOU A,GALLIMBERTI I.Theoretical Modelling of the Development of the Positive Spark in Long gaps[J].Journal of Physics D Applied Physics,1998,27(6):1252-1266.
[21]COORAY V,RAKOV V,Theethayi N.The Relationship between the Leader Charge and the Return Stroke Current-Berger’s Data Revisited[C]//Proceedings of 27thInternationalConference on Lightning Protection .Avignon,France:IEEE,2004:1-6.
[22]COORAY V,BECERRA M.Attractive Radii of Vertical and Horizontal Conductors Evaluated Using A Self-consistent Leader Inception and Propagation Model-SLIM,Atmospheric Research.2012,117(11):64-70.
[23]COORAY V,KUMAR U,RACHIDI F,et al.On the Possible Variation of the Lightning Striking Distance as Assumed in the IEC Lightning Protection Standard as A Function of Structure Height[J].Electric Power Systems Research,2014,113:79-87.
[24]BECERRA M,COORAY V.A Simplified Physical Model to Determine the Lightning Upward Connecting Leader Inception[J].IEEE Transactions on Power Delivery,2006,21(2):897-908.
[25]COMSOL GROUP,COMSOL Multiphysics User’s Guide[k],2008.
[26]BECERRA M,COORAY V,A Self-consistent Upward Leader Propagation Model[J].Journal of Physics D Applied Physics,2006,39(16):3708-3715.
[27]郄秀书,刘欣生,余哗,等.地面电晕离子对空中引雷始发过程的影响.高原气象,1998,17(1):84一94.QIE Xiushu,LIU Xinsheng,YU Ye.Electrostatic Characteristics Near Ground Under Thunderstorm and Its Effect on Artificial Triggering Lightning.Plateau Meteor,1996,15(s):293-302.
[28]郄秀书,言穆弘.雷暴下近地面电特性及其对人工引雷的影响.高原气象,1996,15(s):293一 302.QIE Xiushu,YAN Muhong.Influence of Corona Ions Near the Ground on the Initiation of Altitude Triggering Lightning.Plateau Meteor,1988,17(1):84 一 94
[29]任晓毓.闪电先导与地物相互作用的模拟研究[D].北京:中国气象科学研究院,2010.
Simulation Study on the Lightning Strike Probability of the Tip of Complex Buildings
WANG Menghan1,HOU Wenhao1,ZHANG Qilin1,SHEN Yuan2
(1.Key Laboratory of Meteorological Disaster,Ministry of Education(KLME)/Joint International Research Laboratory of Climate and Environment Change(ILCEC)/Collaborative Innovation center on Forecast and Evaluation of Meteorological Disaster(CIC-FEMD)/Key Laboratory for Aerosol-Cloud-Precipitation of China Meteorological Administration,Nanjing University of Information Science&Technology,Nanjing 210044,China.;2.Yunnan Power Grid Co.,Ltd Electric Power Research Institute,Kunming 650217,China.)
In the Cloud-to-Ground( CG)lightning connection process,the positive polarity upward connecting leader inception and propagation is one of the key factors which determines whether a ground structure is striked by lightning downward leader.At present,the rolling sphere method widely used in buildings to determine the point of lightning strike does not consider the inception process of upward positive leader.Therefore,based on physics leader model which takes full consideration leader and connecting process,the author chooses different shapes of buildings to study the probability of the lightning strike points.By estimating stable upward leader background electric field at the corners of complex structures,the probability of the lightning strike points are determined.The results show:When the downward leader approaches ground buildings,the location of upward leader first initiated becomes the most likely lightning strike points.In addition,the geometry of the buildings and surroundings significantly influences the conditions necessary to estimate the lightning strike points.It is provided that a good basis on the analysis of situation for the building struck by lightning and the lightning protection solutions for buildings.
lightning strike points;upward positive leader;complex buildings;lightning protection
10.16188/j.isa.1003-8337.2017.03.003
2016-04-28
王梦寒(1992—),女,硕士,主要从事雷电物理和监测预警方面的研究工作。
电网雷电预警技术研究及雷电预警系统开发(编号:K-YN2013-186);配电网综合防雷体系研究与工程示范(YNKJQQ00000274);国家自然科学基金项目(编号:41275009)。

