基于R语言的AMMI和GGE双标图在花生区试中的应用

郭敏杰，邓 丽，任 丽，谷建中

(开封市农林科学研究院，河南 开封 475000)

基于R语言的AMMI和GGE双标图在花生区试中的应用

郭敏杰，邓 丽，任 丽，谷建中*

(开封市农林科学研究院，河南 开封 475000)

以2014年河南省小粒花生品种区域试验的数据为材料，选取19个品种，9个试点，利用基于R语言的AMMI和GGE双标图分析花生品种的适应性、丰产性和稳产性，试点环境的相关性、区分力和代表性，为花生品种产量稳定性评价和推广提供有力的支撑。结果表明，高产稳产品种为开农1760、粮花8号、开农1768、农花10、信花425和豫花65号；信阳和新郑，开封和驻马店的生态区域相似，郑州与信阳可能属于不同的生态区域；理想的试点为南阳、濮阳和驻马店。AMMI模型与GGE双标图在品种评价方面结果基本一致，但GGE双标图更加全面。AMMI模型可以合理有效地分割平方和，GGE双标图可以更加全面有效地评估品种和试点。

花生；AMMI模型；GGE双标图；品种评价；试点评估

花生是我国主要油料作物，高产稳产一直是我国育种者的首要育种目标，区域试验是对参试品种的丰产性、稳产性、抗逆性和适应性进行评估，为品种的推广利用提供科学依据，其实质是将不同的基因型放入相同的环境以观察其表现，分析基因型与环境的互作关系(G×E)，选择适应生产和社会需求的品种[1]，所以使用恰当准确的分析方法就显得尤为重要。

作物在生长过程中，G×E对产量的影响较大，对此科研人员提出了多种方法，如方差分析、主成分分析、Finlay&Wilkinson联合回归模型、主效可加互作可乘的AMMI模型和GGE双标图等。长期以来，研究区试数据主要采用方差分析法[2-3]，它考虑基因型、环境和G×E，但这种模型只给出了主效应，将G×E作为一个整体给出，当数据是二向表时，该模型就不能将G×E从残差中分离出来。Finlay和Wilkinson提出了用线性回归的方法描述G×E[4]，它可以解释基因型受环境影响的程度，但是这种模型只是通过一个回归系数来描述G×E。AMMI模型是Finlay&Wilkinson模型的进一步拓展，Guach[5]对AMMI的研究与应用进展进行了综述，它将方差分析和主成分分析相结合，将乘积形式的交互作用加入到基因型和环境的加性模型中，不仅能分析G×E的显著性，还能估计出G×E的特点及形态，目前AMMI模型已经广泛应用到了烤烟[6-7]、水稻[8-10]、西瓜[11]、小麦[12]、土豆[13]等植物评价中。Yan[14]提出的GGE双标图分析法，同时考虑了基因型和G×E效应，能更直观高效地评价和展示G×E，可以广泛地应用于区域试验中的品种评价、试点评价和品种生态区划分[15-19]。

目前，AMMI模型和GGE双标图在花生上的应用鲜有报道，只有陈四龙[20]和吴昌湛[21]用GGE双标图分别分析了种植密度对高油花生生长的影响和花生品种稳定性，但是同时利用AMMI模型和GGE双标图联合分析区域试验中参试品种的丰产稳产性、试点区分力及生态区域划分的研究还未见报道。R语言是开源免费的软件，它具有跨平台特性，在Windows、Linux、Unix和Mac OS系统上都可以运行，操作简单，并且有强大的统计和作图功能。

本文以2014年河南省小粒花生品种区域试验数据为材料，利用AMMI模型和GGE双标图联合分析，以揭示各个参试品种的适应性、丰产性和稳产性，试点区分力、代表性及试点生态区域划分，为精准的评估优异品种和参试点的有效性提供了重要依据，同时也为参试品种能否晋级参加生产试验提供了决策支持。

1 材料方法

1.1 试验材料

以2014年河南省小粒花生品种区域试验的品种荚果产量和试点为资料进行AMMI模型和GGE双标图分析。参试品种19个，试点9个，主要气象因子数据见表1，参试品种名称、试点及代码见表2，参试品种在各个试点的产量见表3。

表1 主要气象因子数据

1.2 试验方法

1.2.1 试验设计

各个试点统一采用随机区组排列，重复3次。小区长6.67 m，宽2.00 m，每个小区种植6行，行距33.33 cm，穴距16.67 cm，每公顷180000穴，每穴2粒。于5月22日左右播种，施肥水平及田间管理均按照河南省小粒花生区域试验方案执行，9月20日左右收获，收获晒干后严格测定各小区花生荚果产量，分析数据时折合成标准产量(kg/hm2)。

1.2.2 数据分析方法

本文采用的AMMI模型和GGE双标图分别是基于R软件的agricolae包[22]和GGE BiplotGUI包[23]。程序如下：

######## 读取数据 ####################

a<- read.table("d:/data.txt",sep="〗t")

head(a)

names(a) <-c("G","E","yield")

head(a)

########AMMI模型程序代码 #########

library(agricolae)

model<-AMMI(ENV=a$E,GEN=a$G,

REP=1,Y=a$yield,MSE=2,console=TRUE)

plot(model,first=0,second=1,type=1,number=F,xlab="Maineffect",

ylab="IPCA1 (43.44ofGE)",main="MeanyieldvsIPCA1:AMMIplot")

########GGEBiplot模型程序代码 #####

library(GGEBiplotGUI)

library(reshape2)

fen_a<-dcast(a,formula=G～E)

head(fen_a)

row.names(fen_a) <-fen_a$G

head(fen_a)

GGEBiplot(fen_a)

(一)AMMI模型分析法

AMMI模型将G×E进行多个维度的分解，从而对G×E解释得更加全面[24]。模型如下：

其中yij为第i个基因型在第j个环境的产量， μ是整体均值， Gi是第i个基因型的效应值，Ej是第j个环境的效应值，G×E被分解为k个因素相乘， bik是基因型得分， Zjk是环境得分，二者是对G×E进行主成分分析的结果，εij为试验残差[25]。

(二)GGE双标图分析法

其中yij为第i个基因型在第j个环境的产量，μ是整体均值，Ej是第j个环境的效应值，基因型效应和G×E被分解为k个因素相乘，bik是品种得分，zjk是环境得分， εij为试验残差[25]。

2 结果与分析

2.1 AMMI模型分析结果

2.1.1AMMI模型分解变异

对荚果产量进行AMMI模型分析(表4)，结果表明，品种、环境和G×E均达到极显著水平，其中品种的平方和占总变异的10.08%，环境间的平方和是变异的主要来源，占总变异的68.25%，G×E的平方和占总变异的21.66%，G×E分解的IPCA1(第一主成分)和IPCA2(第二主成分)分别占G×E的43.44%和20.49%，IPCA1和IPCA2共解释了G×E平方和的63.93%，这也表明了，AMMI模型可以合理有效地剖分平方和[13]。

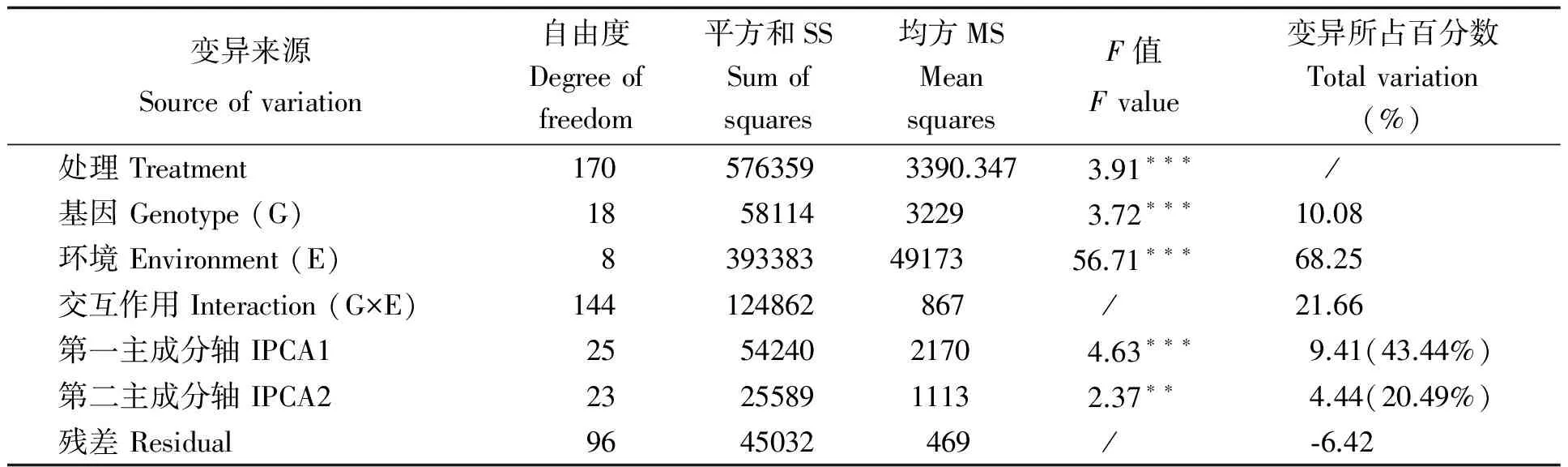
表4 AMMI模型变异分析

注：***表示达到极显著差异(P<0.001)；**表示达到极显著差异(P<0.01)。

Note: ***Represents significant difference atP<0.001; **Represents significant difference atP<0.01.

2.1.2 AMMI模型分析参试品种的丰产稳产性和适应性

以平均产量为X轴，以G×E分解的IPCA1为Y轴，以IPCA1值为0作一条水平线，以所有品种的产量均值作一条垂直线(图1)。水平方向上，横坐标越大，品种产量越高；垂直方向上，越靠近水平线，品种产量越稳定。产量高于对照的高产品种为G2>G5>G8>G11>G14>G6>G4>G7>G9>G17>G16(CK)，产量低于对照的品种为G18G1>G4>G13>G11>G2>G17>G15>G12>G8>G5>G16(CK)；由此得出高产稳产品种有G2、G5、G8、G11、G14和G4。

在水平方向上，试点比品种分散，表明试点间的变异远大于品种间的变异；水平线上下的品种与位于同侧的试点有正向互作，即对品种产量的提高有积极作用品种G10、G18、G19、G16、G15、G12和G13在试点E6、E5、E2、E9有较好的适应性，品种G3、G7、G6、G9、G8、G5、G17、G2、G11在试点E3、E4、E7有较好的适应性。

2.2 GGE双标图分析结果

2.2.1 GGE双标图分析参试品种的适应性

将试点分组(图2)，把最外围的品种顺序连接形成一个多边形，由原点发出的多条射线垂直于各边，从而把多边形分割为7个扇区，这样9个环境就可以分为三组，试点E3和E4为一组，E1、E7、E8为一组，E2、E5、E6、E9为一组，划分为同一组的环境生态区域类似，各扇区内的环境比较适合其区内的品种。各扇区内位于多边形顶角的品种就是该区内的高产品种，如E2、E5、E6、E9区域中G2和G5为高产品种。

图1 AMMI模型双标图 图2 GGE双标图分析品种的适应性 Fig.1 Biplot of AMMI model Fig.2 GGE biplot showing the yield adaptability of 19 varieties

2.2.2 GGE双标图分析各个试点的环境关系

环境相关性评价可以直观地分析各试点对品种评价的相似性(图3)，连接原点和各环境的直线称为向量，两环境向量夹角的余弦值近似于它们的遗传相关系数，夹角越小，说明环境对于参试品种的排序越相似，夹角小于90度为正相关，大于90度为负相关。图中多数环境之间存在正相关，如E1、E7、E8、E3、E4之间；一些环境之间存在着紧密的正相关，如E7和E8，E2和E9；少数环境存在着微弱的负相关，如E5、E6与E1、E7、E8之间，表明这些试点可能属于不同的生态区域。如E5和E6分别为郑州和温县，二者显示正相关，而实际上两者的地理位置非常接近，气候条件比较类似。而E1和E7分别为安阳和信阳，二者与郑州和温县距离较远，双标图也可看出两者之间不相关。值得注意的是，生态区划分需要多年数据并结合实际的气象数据来验证，但双标图无疑可提供一个参考[26]。

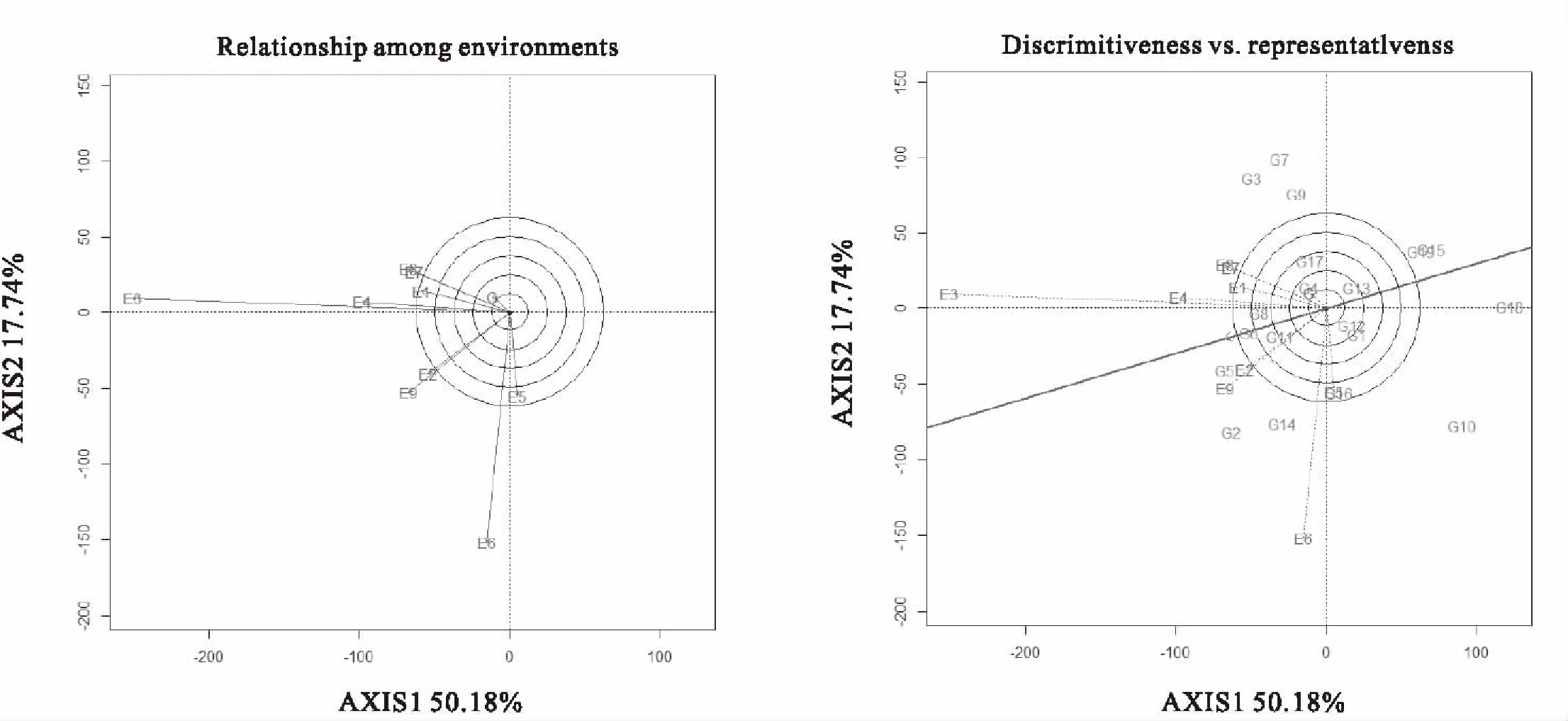
图3 GGE双标图分析环境间相关性 图4 GGE双标图分析试点的区分力和代表性 Fig.3 Environmental vector view of the GGE biplot Fig.4 Discrimination and representativeness view of the GGE biplot

2.2.3 GGE双标图分析试点的区分力和代表性

通过原点和平均环境且带箭头的直线为“平均环境轴”，“平均环境轴”箭头所指方向是对试点区分力和代表性两方面的综合评价[27]；由原点到试点的长度表示该试点的区分力，长度越长，区分力越强，反之越弱；试点向量与平均环境向量的夹角表示试点的代表性，角度越小，代表性越强，反之越差，若是钝角，则该环境不适合做试点。E3、E6、E4、E9区分能力强，E2、E9、E3、E4代表性强(图4)。没有区分力的试点是没有用的，如E1。有区分力但没有代表性的试点可用于淘汰不稳定的品种，但不能用于选择优良品种，如E6，它的区分力比较强但代表性较差。区域试验中试点的选择直接关系着育种的成效，理想的试点需要对品种有较强的区分力、对目标生态区有较强的代表性[28]，所以本文中理想的试点为E3、E4、E9。

以平均环境点为圆心画圆，可综合考虑环境的区分力和代表性(图5)，越靠近中心圆的环境其区分力和代表性越好[29]，所以试点的综合顺序为E3>E4>E9>E2>E8>E7>E1>E6>E5，其中E3、E4、E9是较为理想的试点，与图4的结果一致。

2.2.4 GGE双标图分析品种的丰产性和稳产性

可以通过GGE双标图揭示各花生品种的丰产性和稳定性关系(图6)。“平均环境轴”的箭头所在的位置代表品种在所有环境下的近似平均产量，越往箭头方向产量越高；与平均环境轴垂直并通过原点的直线代表各品种与各环境相互作用的倾向性，越偏离"平均环境轴"越不稳定。由此，从图中可以看出，产量较高的品种有G2、G5、G6、G14、G8和G11；稳产性较好的品种有G6、G8、G11、G13、G4、G5、G15、G19、G18、G2和G14，但是G18、G15、G19、G13和G4产量较低；由此得出高产稳产品种有G5、G2、G6、G8、G11和G14。

图5 GGE双标图分析试点的综合排名 图6 GGE双标图分析品种的丰产性和稳产性 Fig.5 The comprehensive ranking view of the GGE biplot for testing sites Fig.6 Mean vs. stability view of the GGE biplot

以“平均环境轴”上的箭头为圆心画圆，越靠近中心圆的品种，其丰产性越高且越稳定，由图7可知，丰产性和稳产性都比较好的品种有G5、G6、G8、G11、G2和G14，与图6结果基本一致。

3 讨 论

作物品种的丰产性、稳定性是决定其推广应用价值的主要指标，而在品种评价试验中，试点的选择也是育种人员比较关注的问题[30]，传统的方差分析方法，只能分析品种产量的高低，无法评价品种的特殊适应性。本文首次利用基于R语言的AMMI模型和GGE双标图同时评价了花生区域试验中品种的适应性、丰产性和稳产性，以及试点的区分力和代表性，为加快花生的育种进程提供了参考。

在GGE双标图分析方法提出之前，AMMI模型广泛应用于作物区试数据的分析，目前学者们对这两种方法的优劣仍有不同观点。Gauch等[31]认为AMMI模型优于GGE双标图，因为前者可以分解出基因型效应(G)和G×E，而GGE双标图没有将G和G×E剖分出来，他们认为G决定一般适应性，G×E决定特殊适应性，Piepho[32]也从一般配合力和特殊配合力的角度说明AMMI模型更适合分析双列杂交数据。但是Yan[33]对这些问题进行了系统的比较，他认为GGE双标图同时考虑了G和G×E，在品种生态区划分和基因型评价方面来说优于AMMI模型，另外它在评价试验环境方面同样是有效的工具。我们的研究结果与Yan一致，GGE双标图的优越性在于可以直观地把环境分为若干品种生态区，并揭示各生态区内最适应的品种，同时显示各试点对品种的区分力和对目标环境的代表性，所以GGE双标图更适合区试的数据分析。

图7 GGE双标图分析品种的综合排名Fig.7 The comprehensive ranking view of the GGE biplot for varieties

从本文利用AMMI模型和GGE双标图的结果来看，二者一致认为高产稳产品种为开农1760、粮花8号、开农1768、农花10、信花425和豫花65号，目前除信花425外，其他五个品种均通过了2015年河南省小粒花生品种区试。区试时可以适当去掉一些生态区域相似的试点以减少成本而不影响对品种的评价，如信阳和新郑可以去掉之一。然而本研究在环境相关性评价中发现郑州和新郑属于不同的生态区域，但在实际地理区域中二者却很相近，可通过分析其他年份的区域数据进行进一步的验证。

4 结 论

本文利用AMMI模型和GGE双标图同时对花生区域试验的荚果产量及试点进行了分析，在品种评价方面，二者结果基本一致，但在生态区划分和试点鉴别力方面，GGE双标图功能更为全面。高产但不稳产的花生品种有南花3号，稳产但不高产的品种有豫花60号和豫花66号，高产且稳产的品种有开农1760、粮花8号、开农1768、农花10、信花425和豫花65号。信阳和新郑，开封和驻马店生态区域相似，郑州、温县与安阳、信阳、新郑属于不同生态区域。南阳、温县、濮阳和驻马店区分能力强，开封、驻马店、南阳和濮阳代表性强，最佳试点为南阳、濮阳和驻马店。本研究为选育高产稳产品种以及选择优良的试点提供了一个非常有效的方法。

[1] 严威凯. 农作物品种试验数据管理与分析[M]. 北京：中国农业科学技术出版社, 2015: 197-198.

[2] Gelman A. Analysis of variance[J]. Quality Control & Applied Statistics, 2006, 20(1): 295-300.

[3] 胡希远, 尤海磊, 任长宏,等. 基于协方差阵结构优选的作物品种区域试验分析[J]. 作物学报, 2009, 35(11): 1981-1989.

[4] Montgomery D C, Peck E A. Introduction to linear regression analysis[M]. Wiley, 1992:2775-2776.

[5] Gauch H G, Zobel R W. Identifying mega-environments and targeting genotypes[J]. Crop Science, 1997, 37(2): 311-326.

[6] 黄平俊, 易建华, 蒲文宣, 等. 应用AMMI模型分析烤烟品种的产量适宜性[J]. 中国农学通报, 2013, 29(4): 168-172.

[7] 宋淑芳, 周冀衡, 张一扬, 等. 应用AMMI模型分析云南保山烤烟物理性状的基因与环境互作[J]. 江西农业学报, 2014(12): 1-6.

[8] 赵洋, 郑桂萍, 张文秀,等. 利用AMMI模型分析寒地水稻产量的基因型与环境互作关系[J]. 江苏农业科学, 2015, 43(4): 84-86.

[9] 刘丽华, 胡远富, 陈乔, 等. 利用AMMI模型分析寒地水稻3个品质性状的基因型与环境互作[J]. 作物学报, 2013, 39(10): 1849-1855.

[10] Wen N, Wang J A, Liu Z Q. Analysis of genotypic and environmental effects on cadmium content in rice by AMMI model [J]. Journal of Agro-Environment Science, 2015, 34(5): 817-823.

[11] 王志强, 刘声锋, 郭守金, 等. 用AMMI双标图分析西瓜品种的产量稳定性及试点分辨力[J]. 干旱地区农业研究, 2013(4): 89-93.

[12] Li W, Yan Z, Wei Y, et al. Evaluation of genotype × environment interactions in Chinese spring wheat by the AMMI model, correlation and path analysis [J]. Journal of Agronomy and Crop Science, 2006, 192(3): 221-227.

[13] Mwololo J K, Muturi P W, Mburu M W K, et al. Additive main effects and multiplicative interaction analysis of genotype × environmental interaction among sweetpotato genotypes [J]. Journal of Animal & Plant Sciences, 2009, 2(3): 148-155.

[14] Yan W K, Hunt L A, Sheng Q L, et al. Cultivar evaluation and mega-environment investigation based on the GGE biplot [J]. Crop Science, 2000, 40(3): 597-605.

[15] Donosonanculao G, Paredes M, Becerra V, et al. GGE biplot analysis of multi-environment yield trials of rice produced in a temperate climate [J]. Chilean Journal of Agricultural Research, 2016, 76(2): 152-157.

[16] 严威凯. 双标图分析在农作物品种多点试验中的应用[J]. 作物学报, 2010, 36(11): 1805-1819.

[17] Akcura M, Taner S, Kaya Y. Evaluation of bread wheat genotypes under irrigated multi-environment conditions using GGE biplot analyses [J]. Zemdirbyste-agriculture, 2011, 98(1):35-40.

[18] Frashadfar E, Safari H, Jamshidi B. GGE biplot analysis of adaptation in wheat substitution lines [J]. International Journal of Agriculture & Crop Sciences, 2012, 4(13): 877-881.

[19] Nzuve F, Githiri S, Mukunya D M, et al. Analysis of genotype × environment interaction for grain yield in maize hybrids [J]. Journal of Agricultural Science, 2013, 5(11): 75-85.

[20] 陈四龙, 李玉荣, 程增书, 等. 用GGE双标图分析种植密度对高油花生生长和产量的影响[J]. 作物学报, 2009, 35(7): 1328-1335.

[21] 吴昌湛, 韦汉文, 苏明,等. 用GGE双标图分析贺油花生品种产量稳定性及试点代表性[J]. 中国油料作物学报, 2016, 38(1): 47-51.

[22] Mendiburu F, Simon R. Agricolae - ten years of an open source statistical tool for experiments in breeding [J]. Agriculture and Biology, 2015. DOI: 10.7287/peerj.preprints.1404v1.

[23] Frutos E, Galindo M P, Leiva V. An interactive biplot implementation in R for modeling genotype-by-environment interaction [J]. Stochastic Environmental Research & Risk Assessment, 2013, 28(7): 1629-1641.

[24] Gabriel K R. Least squares approximation of matrices by additive and multiplicative models [J]. Journal of the Royal Statistical Society, 1978, 40(2): 186-196.

[25] Marcos M, Jean-Marcel R, Van E F A. The statistical analysis of multi-environment data: modeling genotype-by-environment interaction and its genetic basis [J]. Frontiers in Physiology, 2013, 4(4):44.

[26] 罗俊，许莉萍，邱军，等. 基于HA-GGE双标图的甘蔗试验环境评价及品种生态区划[J]. 作物学报, 2015, 41(2): 214-227.

[27] Yan W, Holland J B. A heritability-adjusted GGE biplot for test environment evaluation [J]. Euphytica, 2010, 171(3): 355-369.

[28] Yan W. GGEbiplot-a windows application for graphical analysis of multienvironment trial data and other types of two-way data [J]. Agronomy Journal, 2001, 93(5): 1111-1118.

[29] Jalata Z. GGE-biplot analysis of multi-environment yield trials of barley (HordeiumvulgareL.) genotypes in southeastern Ethiopia highlands [J]. International Journal of Plant Breeding & Genetics, 2011, 5(1): 59-75.

[30] 李本贵, 阎俊, 何中虎, 等. 用AMMI模型分析作物区域试验中的地点鉴别力[J]. 作物学报, 2004, 30(6): 593-596.

[31] Hgjr G, Piepho H P, Annicchiarico P. Statistical analysis of yield trials by AMMI and GGE: further considerations [J]. Crop Science, 2008, 48(3): 866-889.

[32] Piepho H P. Multiplicative models for specific combining ability in half-diallels with parents [J]. Crop Science, 2013, 53(6): 2321-2331.

[33] Yan W. GGE biplot vs. AMMI graphs for genotype-by-environment data analysis [J]. Journal of the Indian Society of Agricultural Statistics, 2011, 65(2): 181-193.

ApplicationofRLanguageBasedAMMIandGGEBiplotonRegionalTrialofPeanutVarieties

GUO Min-jie, DENG Li, REN Li, GU Jian-zhong*

(KaifengAcademyofAgricultureandForestry,Kaifeng475000,China)

The data of regional trial for small grain peanut varieties in Henan province in 2014 were adopted, of which nineteen varieties and nine testing sites were analyzed. AMMI and GGE biplot based on R language were used to analyze the adaptability, high-yield, stability of peanut varieties and the relevance, discrimination, representativeness of testing sites, so as to provide strong support for the evaluation of yield stability and promotion of peanut varieties. The results showed that Kainong1760, Lianghua8, Kainong1768, Nonghua10, Xinhua425 and Yuhua65 were found to be the most ideal varieties with both high yield and high stability. Xinyang and Xinzheng, Kaifeng and Zhumadian were similar ecological sites, while Zhengzhou and Xinyang belong to different ecological sites. The ideal testing sites were Nanyang, Puyang and Zhumadian. The results of AMMI model and GGE biplot were basically identical on evaluating varieties, but the GGE biplot was more comprehensive. AMMI model was able to logically and effectively divide the sum of squares. GGE biplot could evaluate the testing sites and varieties more comprehensively and effectively.

peanut; AMMI model; GGE biplot; variety evaluation; testing site evaluation

10.14001/j.issn.1002-4093.2017.02.004

S565.2037; S11+4

A

2016-12-07

国家花生产业技术体系(CARS-14)；河南省重大科技专项(161100111000)；开封市农业科技攻关(1502007)

郭敏杰(1989-)，女，河南杞县人，开封市农林科学研究院研究实习员，硕士，主要从事花生遗传育种研究。

*通讯作者：谷建中，研究员，主要从事花生遗传育种研究。E-mail:xinkeyan@sina.com