一种基于相似性计算与决策系统的最优解算法∗

朱俚治

（南京航空航天大学信息中心 南京 210016）

一种基于相似性计算与决策系统的最优解算法∗

朱俚治

（南京航空航天大学信息中心 南京 210016）

当今有多种寻找最优解的算法，k-近邻算法、蚁群算法和退火算法都是较为经典的智能算法。k-近邻算法在寻找最优解算法方面有很大的应用价值，因此对k-近邻算法和粗糙集中的决策系统研究之后，提出一种基于相似性计算算法的最优解算法。论文的思路是首先使用k-近邻算法计算两个实例属性之间的距离，其次使用相似性算法对k-近邻算法求得的解进行计算，然后使用决策系统对解的属性作出决策，是一般性的解，还是较优解或是更优解，将相似性算法和决策系统在寻找最优解之中进行应用是论文的创新点。

k-近邻算法；相似性算法；决策系统

1 引言

分类是认识客观世界，形成抽象概念和进行推理决策的基础，所以分类建模是机器学习研究的核心问题之一［1～4］。k-近邻算法通过计算两个实例属性之间的距离来实现实例之间的分类，在进行分类的时候k-近邻算法采用了欧氏距离对实例属性的距离进行了计算，从而达到了分类的目的。

将粗糙集应用于实例的分类［1～4］，由 1982 年Pawlak教授提出。后来经过许多研究者不断地完善粗糙集理论，为符号数据属性简约性、依赖性分析与分类规则学习提供了形式化框架［1～4］。事实上k-近邻算法和粗糙集对实例寻找最优解过程就是实例分类的过程，如果两个实例成功实现了属性上的匹配，那么该实例就找到了最优解。

本文使用相似性算法对k-近邻算法求出的解进行计算，经过相似性计算之后再使用粗糙集中的决策系统对计算的结果做出决策，该解是较优解或还是更优解，从而达到对解好与坏的度量目的，在本文的最后给出了算法分析。将k-近邻算法，决策系统和相似性算法三种算法相互结合在一起形成一种新的寻找最优解算法是本文的创新之处。

2 k-近邻算法

基于实例的学习方法中的最基本的是k-近邻算法。这个算法假定所有的实例对应于n维空间中的点。一个实例的最近邻是根据标准欧氏距离定义的，更精确地讲把任意的实例x表示为下面的特征向量［1］。

其中，ar(x)表示实例x的第r个属性值。那么两个实例 xi和 xj间的距离定义为 d(xi，xj)，其中［1］：

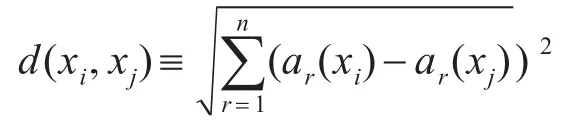
3 k-近邻算法的实现

1）k-近邻算法距离公式

xi，xj分别表示两个训练实例，两个实例属性之间的差值的大小可以使用距离公式来计算［1～3］。

y=d(xi，xj)公式表示实例 xi与 xj分类属性之间的距离，为了找到与实例xi的属性最为接近的实例xj，则这时需要使用距离公式计算出实例xi所有分类属性与实例xj的属性距离，如果找到了与xi最为接近的xj，这时实例xi与xj达到最邻近值。

2）A代表要求分类的实例，该实例有n个属性。am表示实例A进行分类时的能够起到分类作用的属性，B表示储存器中一个的实例，实例B具有的属性bn。

d1表示a1与b1之间的距离，d2表示a1与b2之间的距离，d3表示a1与b3之间的距离，dn表示a1与bn之间的距离。

4 相似性计算法

4.1 相似性函数及其实例属性间的距离

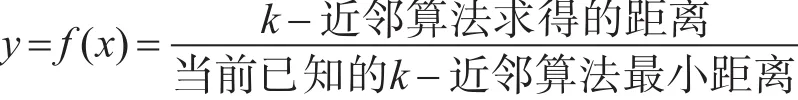
1）在以上的公式中有两种距离：（1）k-近邻算法求得的距离，（2）当前已知的k-近邻算法最小的距离。

2）以下对实例A与实例B之间的距离有下面的讨论和分析：

（1）dn-1为实例A与实例B属性之间的一种距离，该距离的大小为当前已知的k-近邻算法最小距离。

（2）dn为实例A与实例B属性之间的另一中距离，该距离的大小为k-近邻算法求得的距离。

（3）an与bn分别表示是实例 A，实例B的属性。d1表示属性a1与属性b1之间的距离，d2表示属性a1与属性b2之间的距离，d3表示属性a1与属性b3之间的距离…dn表示属性a1与属性bn之间的距离。d1，d2，d3…dn的大小各不相同。

3）关于dn与dn-1的比较有以下的讨论：

（1）dn-1表示属性a1与属性bn-1之间的距离，dn表示属性a1与属性bn之间的距离。

（2）如果dn＜dn-1，那么a1与bn之间的距离小于a1与bn-1之间的距离。

（3）如果 dn-1＜dn，那么 a1与bn-1之间的距离小于a1与bn之间的距离。

4.2 实例A与实例B属性之间的分析和讨论

1）当实例 A与实例B属性之间的距离为dn＜dn-1时：

（1）dn为实例A与实例B属性之间的另一中距离，该距离的大小为k-近邻算法求得的距离，dn-1为实例A与实例B属性之间的一种距离，该距离的大小为当前已知的k-近邻算法最小距离。因此由 dn＜dn-1条件可得如下的结论：

（2）当dn的值越小时，则表明实例A的属性a1与实例B的某个属性bn相似性就越强。如果表明此时实例A的属性a1与实例B的某个属性bn之间的距离更小，实例A与实例B的属性更为接近，因此此时k-近邻算法求得的距离比当前已知的最小k-近邻算法距离更好。

（3）因此当dn＜dn-1之时，则在属性相似度这一方面a1与bn的相似程度强于a1与bn-1的相似程度，因此这时应该选择bn作为a1目前最佳匹配属性。

2）当实例 A与实例 B属性之间的距离为dn-1＜dn时：

（1）dn为实例A与实例B属性之间的另一中距离，该距离的大小为k-近邻算法求得的距离，dn-1为实例A与实例B属性之间的一种距离，该距离的大小为当前已知的k-近邻算法最小距离，因此由 dn-1＜dn条件可以得如下的结论：

（2）当dn的值越大之时，则表明实例A的属性a1与实例B的某个属性bn相似性就越差。如果

在本文中将r设定为函数 y=f(x)的比值。r的含义是度量实例A与实例B相似性的一个相似性系数，体现了实例A与实例B之间的相似度。dn与dn-1表示实例A与实例B属性之间的距离。如果相似系数r的值越小，那么则此时dn的值比dn-1来得更小，那么实例A的属性a1与实例B的属性bn就越相近，那么此时求就得的解就为更优。如果相似系数r的值越大，那么则此时dn的值比dn-1来得更大，那么实例A的属性a1与实例B的属性bn就相差较远，属性的偏离程度较大，那么此时求就得的解就较差。

2）对相似性系数r的讨论：

相似系数r在［0，1］之间变化，如果相似系数r越小，那么实例A与实例B相似性也就越强，这时求得的解也就更优。

（1）当相似性系数r的值小于1时：

如果相似系数r越小或十分接近于0时，那么则实例属性之间的相似性就越强，实例之间相似性解也就更优。

（2）当相似性系数r的值大于1时：

如果相似系数r的值越大时实例A与实例B的属性偏离程度就越严重，实例A与实例B之间表明此时实例A的属性a1与实例B的某个属性bn之间的距离更加偏离，实例A与实例B的属性偏离程度越严重，k-近邻算法求得的距离比当前已知的k-近邻算法最小距离来得更差。

（3）因此当dn-1＜dn之时，则在属性相似度这一方面a1与bn的相似程度弱于a1与bn-1的相似程度，因此此时应该选择bn-1作为a1目前最佳匹配属性。

4.3 相似性计算的相似系数

1）将相似性系数设为：的相似性也就越差，此时求得的解也就更差。

5 粗糙集的决策系统

在实际应用中存在一大类任务：给定一组有特征描述的样本和样本的类别，需要通过一个学习算法从该组本文中学习一个分类函数，实现从特征到分类的映射，粗糙集理论中称该数据集为信息系统［6-7］。

定义1 信息系统可形式化为如下的四元组：IS=U，A，V，f ，其中 U={x1，x2，x3，…，xn}为研究对象的有限集合，即论域；A={a1，a2，a3，…，an}为描述对象的全部属性所组成的集合，即属性集；为属性集A的值域，其中Va为属性a∈A值域；f：U×A→V为信息函数，表示对每一个x∈U，a∈A，f(x，a)∈Va。 当 系 统 中 属 性 集A=C∪D，C∩D=Φ 其中C为条件属性集，D为决策属性时，该信息系统也被称为决策表［7～9］。

6 决策系统在寻找最优解上的计算

由于决策条件属性值的不同，因此能够产生不同的决策属性，事实上正是由于不同的决策的属性值，产生了不同的决策结果，这些不同的决策结果能够将不同属性的样例进行有效的分类［8～9］。条件属性的属性值决策规则的内涵，是决策系统做出决策结果的重要决定因数［8～9］。

6.1 值域和属性集

1）域：

U={x1，x2，x3，…，xn} ，其中分别表示等待求解的实例A。

2）属性集：

A={a1，a2，a3}，其中 a1表示当前 k-近邻算法求得的距离，a2表示相似性系数r，a3表示决策系统的决策值。

3）值域：V={Y，N}

6.2 实例A解的属性决策表

如果在一个决策系统中把每一条样例的条件属性值部分作为规则的前件，把决策属性值部分作为规则的后件，那么每一条样例都可以看成一条规则［8～9］。在决策系统中每一条样例都对应着一条具体的决策规则。信息系统中的属性集合可以分成两部分，一部分为条件属性集合，另一部分为决策属性，这种信息系统通常称为决策系统或决策表［8～9］。在以下的决策表中可将决策属性分为条件属性和决策属性［8～9］。

在以下的系统决策表中，条件属性是：k-近邻算法求得的距离，相似性系数r。决策属性是：实例A与实例B的相似程度。

说明：1）如果k-近邻算法求得的距离，决策属性值为Y。

2）当相似性系数r越小时，决策属性值为Y，否则决策属性值为N。

3）当1）与2）的属性值都取Y时：决策属性值为Y，否则决策属性值为N。

4）当1）与2）的属性值都取Y时：决策系统的决策结果为求得实例A的解为更优。

决策规则：

（k-近邻算法求得的距离，Y）Λ（相似性系数r越小时，Y）⇒（求得实例的解为更优，Y）

（k-近邻算法求得的距离，Y）Λ（相似性系数r越小时，N）⇒（求得实例的解为更优，N）

7 相似性算法的算法分析

现在某个实例A有个n属性，实例B有m个属性，实例A的属性用符号an表示，实例B的属性bm表示。实例A的某个属性a1都要与实例的B每个b1，b2，b3，bm进行距离上的计算。d1表示a1与b1之间的距离，d2表示a1与b2之间的距离，d3表示a1与b3之间的距离……dn表示a1与bn之间的距离。

1）在k-近邻算法中采用蛮力算法寻找最优解总的次数

如果实例A与实例B之间存在比当前的距离更小的距离，那么当前的距离不是最小距离，因此要在n个距离中要找到最小距离，必须与全部的距离比较之后实例A才能够确定该距离是否是最小距离，然而要确定该距离是否为最小距离需要比较的次数是次n-1。

如果实例A共有个n属性值，为了在这n个距离值中找到最小距离，则需要拿d1与个n-1距离进行比较，因此每一个属性必须经过n-1次比较之后才能找到该属性的最小距离。

根据上述分析有以下的结论：

实例A有个n属性值，然而实例A每个属性比较的次数都是n-1，因此n个属性总共需要比较的次数是n×(n-1)次。

2）采用本文提出的算法寻找k-近邻算法的最优解总的次数

由于实例A与实例B之间寻找的是最小距离，然而由于本文提出的算法是实例A的目前距离始终是最小距离，然而事实上d1不一定是最小距离。如果实例A寻找到比d1更小的距离之时d2，那么d2为实例 A目前的最小距离，假如d2为实例A目前的最小距离，但本文提出的算法是需要在n-2个距离的比较中寻找最小距离，那么此时需要比较的最大次数为n-2次。根据以上的分析有如下的结论：

（1）如果d3为实例A目前的最小距离，实例A需要在n-3个距离的比较中寻找最小距离之时，那么此时需要比较的最大次数为n-3次。如果dn为实例A目前的最小距离，dn需要在n-m个距离的比较中寻找最小距离，那么此时需要比较的最大次数为n-m次。

（2）因此本文提出的算法实例A要在n个属性中找到每一个属性的最小距离一般情况下需要比较的次数是：

说明：(n-1)+(n-2)+(n-3)+…+(n-m)，这里一共有 n个(n-1)，(n-2)，(n-3)，…(n-m)。

通过计算的公式：

3）蛮力寻找最优解的算法和本文提出的寻找最优算法的比较

（1）两种算法运行时所需的次数：

蛮力算法的运行次数：（n-1)n。本文提出的算法运行的次数：

（2）分析和讨论：

当n=6

蛮力算法的运行次数：30次，本文提出的算法运行的次数：6次。

当n=14

蛮力算法的运行次数：128次，本文提出的算法运行的次数：14次。

当n=24

蛮力算法的运行次数552次，本文提出的算法运行的次数：24次。

当n=36

蛮力算法的运行次数：1260次，本文提出的算法运行的次数：36次。

当n=58

蛮力算法的运行次数：3306次，本文提出的算法运行的次数：58次。

（3）根据以上的计算和分析有以下的结论：

蛮力算法的运行次数：（n-1)n，本文提出的算法运行的次数相比较之后可以知道：(n-1)n要大于，然而本文提出的算法运行的次数要少于蛮力算法的运行次数，算法要明显优于蛮力算法。

当n的值越大，本文提出的算法运行比较次数将越明显小于一般性算法的运行比较次数，因此本文提出的算法优于一般性算法的程度更为明显。

4）蛮力寻找最优解的算法和特殊情况下本文提出的寻找最优算法的比较

（1）如果需要判断某个距离是否为实例A目前的最小距离，那么这个距离至少与1个距离或几个距离比较过后才能确定。例如当d2是实例A目前最小的距离，那么d2必须d1比较之后，才能够确定d2是实例A目前的最小距离。

假设实例A的一个属性或多个属性都是以d2为目前的最小距离，那么实例A需要在n-2个距离中找到最小距离，这时实例A的每个属性需要比较的次数都为n-2次，因此实例A的n个属性总的比较次数是n(n-2)次。

（2）有以上的分析和讨论可以有以下的结论：

如果采用蛮力算法在寻找最小距离时，即最优解时需要比较总的次数为n(n-1)，而本文提出的算法，在某特殊情况下最大运行次数为n(n-2)。将这两种算法比较之后有以下的结论：n(n-1)-n(n-2)=n2-n-n2+2n=n＞0 ，n(n-1)＞n(n-2)，因此可以知道蛮力算法运行的最大比较次数大于由本文提出的算法运行时所需要的的最大比较次数，由此可知本文提出的算法优于一般性的蛮力算法。

8 寻找最优解的算法

1）使用k-近邻算法计算实例A与实例B属性之间的距离。

2）使用相似性算法对k-近邻算法的解进行计算，寻找较优解或更优解。

3）使用粗糙集中的决策系统对相似性算法的计算结果。

9 结语

本文参考了已有的智能算法之后将相似性计算算法，决策系统和k-近邻算法这三种不同的算法融合到了一起，形成了一种新的寻找最优解算法。该算法首次将相似性计算算法和决策系统这两种算法在寻找最优解的算法中进行应用，这是本文不同于其它算法的地方，也是本文的创新之处。本文提出的算法能够与现有的智能性算法共同使用，起到相互补充的作用，但实际的效果需要在实际的应用中进行检验。

［1］TomM.Mitchell著.机器学习［M］.北京：机械工业出版社，2013.TomM.Mitchell.Machine learning［M］.Beijing：Mechanical Industry Press，2013.

［2］林关成.基于改进K近邻算法支持向量分类研究［J］.渭南师范学院学报，2012（2）：83-86.LIN Guancheng.Support Vector Classification Based on Improved K Nearest Neighbor Algorithm［J］.Journal of Weinan Teachers College，2012（2）：83-86.

［3］陆微微，刘晶.一种提高K-近邻算法效率的新算法［J］.计算机工程与应用，2008（4）：163-178.LU Weiwei，LIU Jing.A New Algorithm to Improve the Efficiency of K-Nearest Neighbor Algorithm［J］.Computer Engineering and Applications，2008（4）：163-178.

［4］桑应宾，刘琼荪.改进K-nn快速分类算法［J］.计算机工程与应用，2009（11）：145-146.SANG Yingbin，LIU Qiongsun.An Improved K-nn Fast Classification Algorithm［J］.Computer Engineering and Applications，2009（11）：145-146.

［5］邵峰晶，于忠清，王金龙，等.数据挖掘原理与算法［M］.北京：科学出版社，2009.SHAO Fengjing，YU Zhongqing，WANG Jinlong，et al.Principles and algorithms of data mining［M］.Beijing：Science Press，2009.

［6］罗森林，马骏，潘丽敏.数据挖掘理论与技术［M］.北京：电子工业出版时，2013.LUO Senlin，MA Jun，PAN Limin.Data Mining Theory and Technology［M］.Beijing：Electronic Industry Publishing，2013.

［8］胡清华，于达仁.应用粗糙集计算［M］.北京：科学出版社，2012年6月.HU Qinghua，YU Daren.Application of Rough Set Computation［M］.Beijing：Science Press，June 2012.

［9］陈德刚.模糊粗糙集理论与方法［M］.北京：科学出版社，2013.CHEN Degang.Theory and Method of Fuzzy Rough Sets［M］.Beijing：Science Press，2013.

［10］朱梧槚，肖奚安.数学基础与模糊数学基础［J］.自然杂志，7（1980）：723-726.ZHU Wujia，XIAO Xi'an.Mathematical Foundation and Fuzzy Mathematics Foundation［J］.Natural J.，7（1980）：723-726.

［11］洪龙，肖奚安，朱梧槚.中介真值程度的度量及其应用（I）［J］.计算机学报，2006（12）：2186-2193.HONG Long，XIAO Xi'an，ZHU Wujia.Mediation degree of truth value measurement and its application（I）［J］.Journal of computer，2006（12）：2186-2193.

［12］茹强喜，刘永.一种提高K近邻分类的新方法［J］.电脑知识与技术，20106（8）：1989-1991.RU Qiangxi，LIU Yong.A New Method for Improving K-Nearest Neighbor Classification［J］.Computer Knowledge and Technology，20106（8）：1989-1991

［13］余小鹏，周翼德.一种自适应K最近邻算法的研究［J］.计算机应用研究，2006（2）：70-72.YU Xiaopeng，ZHOU Yide.An Adaptive K-Nearest Neighbor Algorithm［J］.Application Research of Computers，2006（2）：70-72.

A Similarity Computing and Decision System Based on the Optimal Solution Algorithm

ZHU Lizhi
（Information Center，Nanjing University of Aeronautics，Astronautics，Nanjing 210016）

There is a variety of search for the optimal solution algorithm，k-nearest neighbor algorithm，ant colony algorithm and annealing algorithm is a classical intelligent algorithms，k-nearest neighbor algorithm in the search for the optimal solution algorithm has great application value，so the author of the k-nearest neighbor algorithm and rough set decision-making system research，an algorithm based on similarity computing algorithm of the optimal solution is put forward.The idea of this paper is the first to use k-neighbor algorithm to calculate the distance between the two instance attributes，followed by using similarity algorithm of k-nearest neighbor algorithm，finding the solution to calculate the property of solution and then use the decision-making system decision-making，is a general solution，or the optimal solution or more optimal solution，the similarity algorithm and decision system in the search for the optimal solution for application is the innovation of this article.

k-nearest neighbour algorithm，similarity algorithms，decision support systems

TP301

10.3969/j.issn.1672-9722.2017.11.016

Class Number TP301

2017年5月10日，

2017年6月30日

朱俚治，男，工程师，研究方向：计算机技术与信息安全。