不同闭合压力下测试时间对岩心导流能力的影响

刘 享 ，伊向艺 ，2，王彦龙 ，李 丹 ，李 沁

（1. 成都理工大学能源学院，四川成都 610059；2. 成都理工大学油气藏地质及开发工程国家重点实验室）

不同闭合压力下测试时间对岩心导流能力的影响

刘 享1，伊向艺1，2，王彦龙1，李 丹1，李 沁1

（1. 成都理工大学能源学院，四川成都 610059；2. 成都理工大学油气藏地质及开发工程国家重点实验室）

利用拟三轴岩心夹持器对劈裂岩心进行加压，考察了测试时间对裂缝导流能力的影响。实验表明：随着测试时间的增加，岩心导流能力逐渐降低，60 min之前下降速度较快，60 min之后下降较慢。加压前期，曲线拟合的误差相对较大，随着加压时间的延长，误差逐渐减小。利用拟合公式对加压后期的导流能力进行预测，从而减少实验的工作量。当裂缝处于闭合阶段时，岩石受到压缩，与储层的实际情况相符，此阶段实验结果可用于对储层进行导流能力评价，更真实地反映油藏条件下裂缝导流能力与应力之间的关系。

加压时间；闭合压力；导流能力；裂缝宽度

实验室对导流能力的测量大部分以研究闭合压力对导流能力的影响，很少研究在某一闭合压力下，测试时间对裂缝导流能力的影响。通过改变围压进行导流能力实验，每一个围压的改变需要一段时间达到相对稳定[1–3]。测试裂缝导流能力的闭合时间越短，实验效率越高，但实验数据的准确性较低。因此，在测定裂缝导流能力的过程中，多长闭合时间所获得的实验数据更准确对于研究裂缝短期导流能力具有重要的参考作用。

1 实验步骤

实验选取6块岩心，岩心参数见表1。岩心全部来自塔河油田碎屑岩储层，岩石主要以细粒结构为主，砂岩以中粗粒砂状结构为主，平均粒径 0.12～0.31 mm；胶结物中含有方解石，岩心中石英含量达到90%以上。

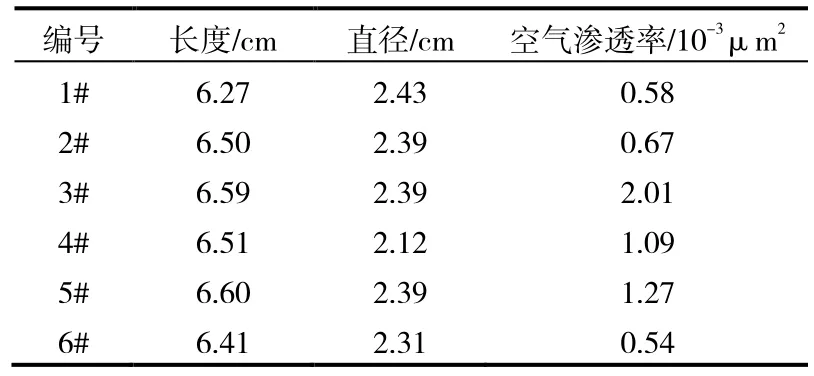
表1实验岩心基础数据

实验步骤为: ①对岩心进行纵向人工造缝，清除断面上的破碎颗粒，将两部分用胶带固定，放入岩心夹持器中；②围压设为4 MPa；向岩心中注入配好的标准盐水，直到岩心另一端出水时开始计时，测定其实际流量；③每隔30 min测定出口的实际流量；④改变围压重复前三步，测定其它岩心的围压分别为5 MPa，10 MPa，15 MPa，20 MPa，25 MPa。

2 实验结果及分析

导流能力随闭合时间的变化用导流能力下降率表示[4]， 导流能力下降率 = （初始导流能力－任意时刻导流能力）÷ 累计闭合时间。

实验结果（图1）表明：①随着时间的增加，导流能力逐渐降低；②在加压初期，导流能力下降较快，下降率10%～22%；③60 min之后，导流能力下降速度减慢。

对岩心实验数据进行处理，发现幂函数很好地拟合实验曲线（表2），拟合表达式为：

式中：C为裂缝导流能力，10–3μm2·cm/min；T为裂缝闭合时间，min；a，b为系数。

由图2可以看出，闭合压力与b值有一定的相关性；通过拟合，得到b值与闭合压力的关系为：

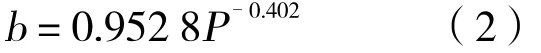
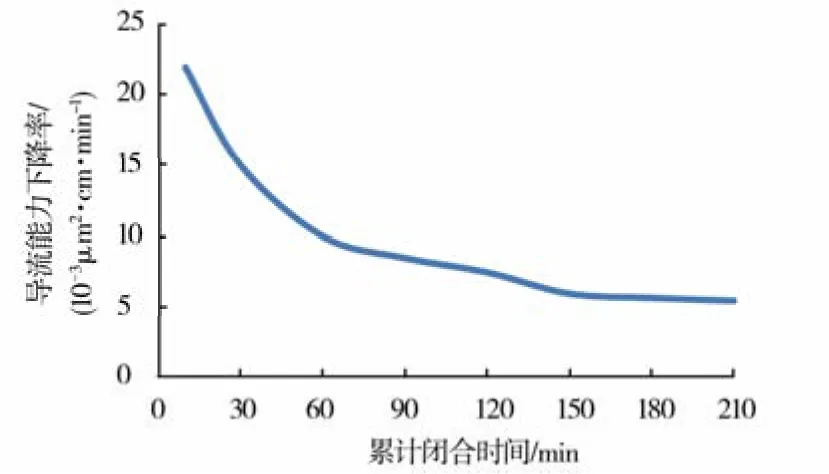
图1 导流能力下降率与闭合时间关系

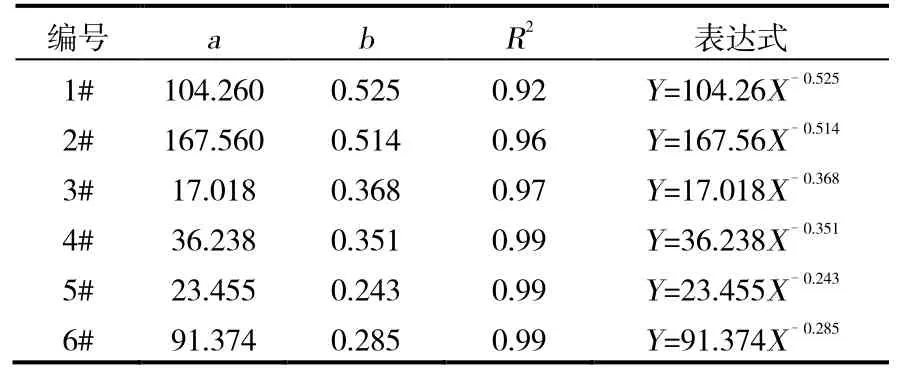
表2 不同岩心实验拟合参数统计

图2 b值与闭合压力的关系曲线

由图3可看出，双对数坐标中，a值与初始导流能力有很好的线性关系；通过拟合，a值和初始导流能力在双对数坐标中呈线性关系，由此可得到：

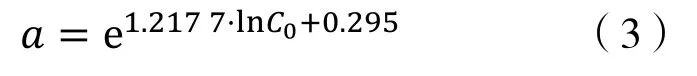
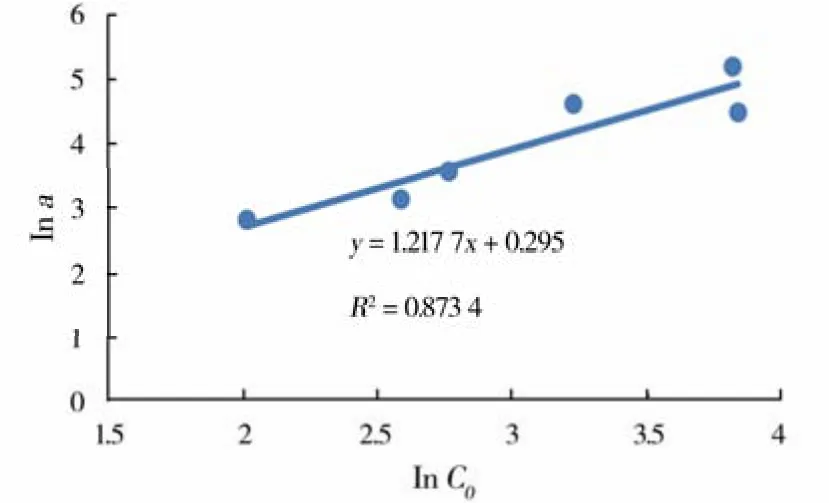
图3 a与初始导流能力的关系曲线

利用拟合的导流能力公式，计算不同闭合时间下的裂缝导流能力；利用拟合公式求得15 MPa围压下导流能力随闭合时间的变化，对比计算值与实测的裂缝导流能力。由图4可看出，加压前期曲线拟合的误差相对较大；随着加压时间的延长，误差逐渐减小。利用拟合公式对加压后期的导流能力进行预测，从而减少实验工作量。

图4 导流能力实测值与计算值对比

3 裂缝宽度预测

式中：Kf为裂缝渗透率，10–3μm2；W为裂缝宽度，μm；D为裂缝间距，cm；

裂缝导流能力与裂缝宽度关系为：

把实验得到裂缝导流能力和加压时间进行回归得到幂指数关系代入公式（4）和（5）：得到裂缝宽度与加压时间的关系：

前人研究得到的裂缝宽度与渗透率的关系为[5]:

由图5可看出，60 min之前裂缝宽度减小速度较快，60 min之后减小速度逐渐变缓，它与导流能力随时间的变化具有相同规律。本文引用平行板模型将裂缝假设成理想的平行板模型，没有考虑实际裂缝两表面的粗糙程度的影响。在实际裂缝中，裂缝表面的形态十分复杂，多组裂缝之间互相交错，裂缝的延伸方向变化不定等，会对裂缝内流体的流动会产生极大的影响。因此，本文利用该模型预测的裂缝宽度只能作为一个参考，实际应用中则需要进一步考虑各种因素。

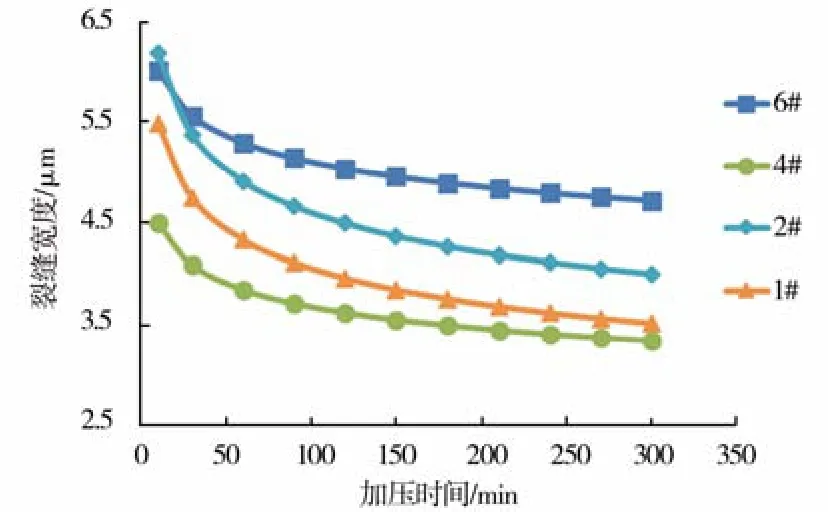
图5 不同岩心裂缝宽度随加压时间变化预测

4 结论

（1）裂缝导流能力随加压时间的延长而减小，以60 min为拐点，60 min之前导流能力下降较快，60 min之后下降缓慢。

（2）加压前期曲线拟合的误差相对较大，随着加压时间的延长，误差会逐渐减小。因此，可以利用拟合的公式对加压后期的导流能力进行预测，从而减少实验的工作量。

（3）当裂缝处于闭合阶段时，岩石受到压缩，与储层的实际情况相符，此阶段的实验结果可用于对储层进行导流能力评价，更真实地反映油藏条件下裂缝导流能力与应力之间的关系。效应力作用时间的响应[J]. 钻采工艺，2007，30（3）：105–107.

[2] 高艳霞. 川西致密储层岩石力学特性及裂缝应力敏感性研究[D]. 四川成都：成都理工大学，2008.

[3] 纪国法，张公社，许冬进，等.页岩气体积压裂支撑裂缝长期导流能力研究现状与展望[J]. 科学技术与工程，2016，16（14）：78–88.

[4] 邱小龙，伊向艺，岳晓军，等. 闭合时间对裂缝导流能力影响实验研究[J]. 中外能源，2012，17（9）：55–57.

[5] 李莹. 裂缝间距分布规律对导流能力的影响研究[D]. 四川成都：成都理工大学，2013.

[6] 郭保华，田采霞. 岩石裂隙的法向蠕变及渗流的影响[J].河南理工大学学报(自然科学版)，2012，31（4）：403–408.

[7] 李俊，林锋，孟陆波，等. 变加载方式灰岩蠕变试验研究[J]. 科学技术与工程，2015，15（28）：67–70.

TE357

A

1673–8217（2017）06–0119–03

2017–04–18

刘享，硕士研究生，1991年出生，2015年毕业于成都理工大学能源学院石油工程专业，现为成都理工大学硕士研究生，研究方向为储层保护与储层改造。基金项目：国家自然科学青年基金“碳酸盐岩储层酸岩反应表面形态与演化”（51504200）。

张 凡

[1] 王业众，康毅力，张浩，等. 碳酸盐岩应力敏感性对有