快 速 液 质 联 用 数 据 峰 对 齐 算 法
孙 萧 寒
(渭南师范学院 网络安全与信息化学院, 陕西 渭南 714000)
快速液质联用数据峰对齐算法
孙 萧 寒
(渭南师范学院 网络安全与信息化学院, 陕西 渭南 714000)
液质联用(LC/MS)是一种将物理分离能力和质量分析能力相结合的技术,可用于检测内源性小分子代谢物,近年来在代谢组学研究中被广泛应用。然而该技术在输出检测出的离子峰数据时往往具有很强的噪声,并且在保留时间上出现样本间的非线性偏差,因此必须对LC/MS输出的数据在各样本间进行峰对齐。现有的LC/MS数据对齐方法由于结构复杂、参数设置较多而不适用于快速峰对齐。针对此问题提出快速LC/MS数据峰值对齐算法。该算法包括数据预处理、峰识别和峰匹配3个模块,无需用户选择参数,时间复杂度低。
液质联用; 峰对齐; 代谢谱
0 引 言
代谢组学(metabolomics)研究特定的分子过程所遗留的独特化学标志,其研究对象为代谢物图谱[1-2]。代谢组学需要检测并收集大量的代谢物数据,目前用于检测代谢物的主要技术是核磁共振波谱技术与质谱分析技术[3-4]。近年来,高效液相色谱分离技术与质谱检测技术的结合(LC/MS),因其具有的高通量、软电离和代谢物覆盖全的特点已经成为代谢组学研究中检测小分子化合物的主流平台[5-6]。LC/MS数据包括3个维度:保留时间、质量电荷比(m/z)和离子峰强度。在某一质量电荷比下,离子峰强度曲线所形成的峰的部分即可能对应小分子化合物。
然而,由于实验技术、实验设备、实验环境等因素的影响,不同样本的离子峰强度曲线不尽相同,且峰的部分在保留时间上存在偏差,这种偏差会直接导致小分子化合物检测与识别的错误[7]。此外,峰的偏差也表现在峰的形态(峰的高度,峰的宽度,峰的形状)上,因此在进行小分子化合物分析前必须先将离子峰对齐。
现有的LC/MS数据对齐方法一般存在两个问题[8-9]:① 需要选择参数,并且峰对齐的结果对参数特别敏感;② 方法的时间复杂度高。以最主流的XCMS为例,不管是下载安装R版本的软件还是在线提交数据,当数据量较大时,往往需要几天甚至更长的等待时间[10]。针对现有方法参数敏感和时间复杂度高问题,本文提出快速LC/MS数据峰对齐算法。
1 实验方法
快速LC/MS数据峰对齐算法包括数据预处理、峰识别和峰对齐3个模块(见图1)。

图1 流程图
1.1 数据说明
本实验数据采用Ralf Tautenhahn等公开的数据(http://msbi.ipb- halle.de/msbi/centwave/),包括121个样本,每个样本包括2 972个保留时间点(保留时间点作为保留时间的刻度),时间范围从0.491~999.924 s(每个时间点间隔为0.336 s);每个样本在每个保留时间点均检测质量电荷比和对应的离子峰强度。其中检测出的质量电荷比的范围94~1 005,离子峰的强度10~15 231。
1.2 数据预处理
由于LC/MS技术检测出的质量电荷比是一个精准数据,故可以选择统一的质量电荷比步长(本文选择0.5),取该质量电荷比步长范围内每一个保留时间点上最大的离子峰强度数据作为该保留时间点上的离子峰强度数据[11]。
(1) 峰形态分析。观察每一个质量电荷比数据,发现离子峰强度在保留时间的维度上呈Z字形状(见图2)[12],即离子峰强度在某一保留时间点很强,在下一保留时间很弱或为0(检测不到),但在第3个保留时间又增强,依次变化。
如果观察整个保留时间段内离子峰强度最大的质量电荷比,可以发现在一段保留时间点内,总是有2个具有最大离子峰强度的质量电荷比此消彼长。这种Z字形的离子峰强度数据应该是由于在同一质量电荷比、同一保留时间段内有不只一个小分子化合物被检测到,但由于实验设备或技术原因导致一个质量电荷比的离子峰强度被另一个所遮蔽。

图2 离子峰强度Z字形态
(2) 数据降噪。由于原始离子峰强度数据的Z字形态并不符合自然情况,故使用离子峰强度与保留时间所形成的二维折线的面积代替原始的离子峰强度数据,并基于面积数据采用小波变换进一步降噪。
由于LC/MS数据的噪声高且其噪声特征未知,而小波降噪可以对信号去噪且能很好刻画信号的非平稳特征,Salvatore等的实验也证明基于非抽样的离散小波变换更适合于LC/MS数据降噪[13]。本方法所采用的小波降噪的具体参数如下:多贝西小波(Daubechies Wavelet)db2、3层分解重构、最大重复离散小波转换、软阈值、根据每一层小波分解的噪声水平估计进行调整。去噪后数据如图3所示。
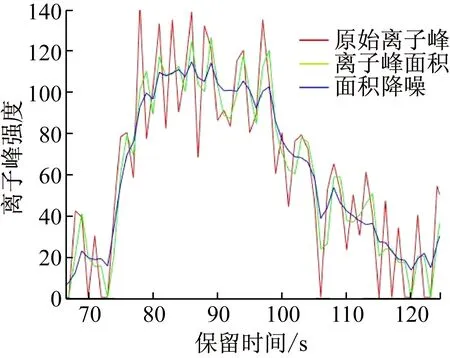
图3 小波去噪曲线(质量电荷比:980.123~980.625)
1.3 峰识别
LC/MS数据的峰识别是要从离子峰强度中识别出由小分子化合物所引起的峰而过滤掉随机噪声。然而仅从离子峰强度很难区分丰度小的小分子化合物引起的峰与噪声所引起的峰[14]。本文采用候选峰识别和候选峰过滤两步方法进行峰识别。
(1) 候选峰识别。本方法采用

来定义峰:峰是由峰头与峰尾所界定的一截保留时间段。峰头是加速度由负值或0值变为正值的保留时间点;峰尾是加速度由正值变为负值或0值的保留时间点。
加速度的定义是基于离子峰强度所围区域的面积,这意味如果一旦一个离子峰强度被抑制超过一个保留时间点就有很大的可能发生加速度符号的变化,此时一个完整的峰会被识别为两个独立的峰。为了将分离峰进行合并,本文设计了相邻峰合并测度,
[25]胡奇馨:《宋代银铜矿考》,载《福建社会》第二卷1、2期合刊;《福建经济发展简史》,第163页,厦门大学出版社,1989年。

其中峰距=后峰峰头-前峰峰尾。经多次实验,选取经验值MNP≥7时,合并相邻峰。
(2) 候选峰过滤。仅由加速度所识别的候选峰含有由噪声所引起的峰,为消除噪声峰,本文基于降噪数据识别可能的峰顶点。由于LC/MS的各样本的离子峰强度差异较大,所以根据降噪后数据单独估计每一个样本的经验累积分布密度,选取累积分布密度≥95%的保留时间点。在这些保留时间点中选择其离子峰强度高于其前一保留时间点及后一保留时间点的数据点作为峰顶点。对前一步得到的候选峰采用峰顶点进一步筛选,只有那些包含有峰顶点的候选峰才作为识别出的峰(见图4)。
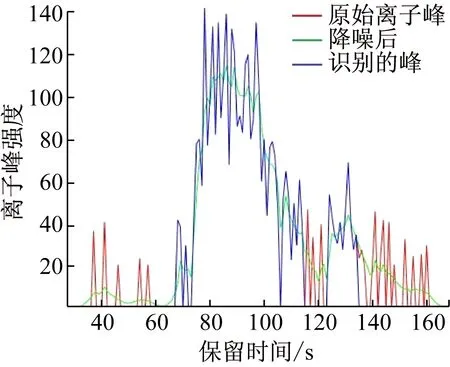
图4 峰识别(质量电荷比:980.123~980.625)
1.4 峰对齐
(1) 峰匹配矩阵。基于每一个样本所识别出的候选峰,对2个样本间的候选峰两两进行匹配,并计算匹配值mv。首先根据LC/MS原始数据计算每一保留时间点的斜率和面积,并基于此计算2个样本的候选峰之间匹配段的斜率余弦相似度和面积余弦相似度,以其和作为度量值,其中和最大的匹配段即为2个样本间的匹配候选峰,
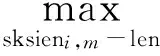
(hl+len-1),areaj_n(l1i+len-1))
(1)
式中:i,j是样本号;m,n是候选峰号;k,l是候选峰中保留时间点;len是2个候选峰中较短的候选峰长度(len=min(leni_m,lenj_n))。由此,得到任意2个样本间的候选峰匹配矩阵。
pvin,jn=abs(starl pvintpeaklm-start pointpeakjn+
(2)
式中,pv为最小的匹配段,即为两样本间的匹配峰。
此外,由于样本间候选峰数也不一样,存在某一个样本的一个峰被匹配另一样本多个不同的峰的可能性。此时,取峰匹配段距离最接近的峰作为匹配峰。
2 结果与分析
本方法是基于原始数据的形态(每一时间点的斜率和面积)及峰之间的距离进行样本间离子峰对齐。对识别出的峰按过滤后的峰匹配矩阵移动各样本中的峰,最终形成峰对齐曲线(见图5)。
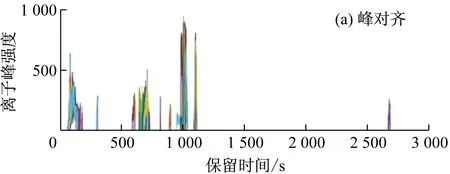
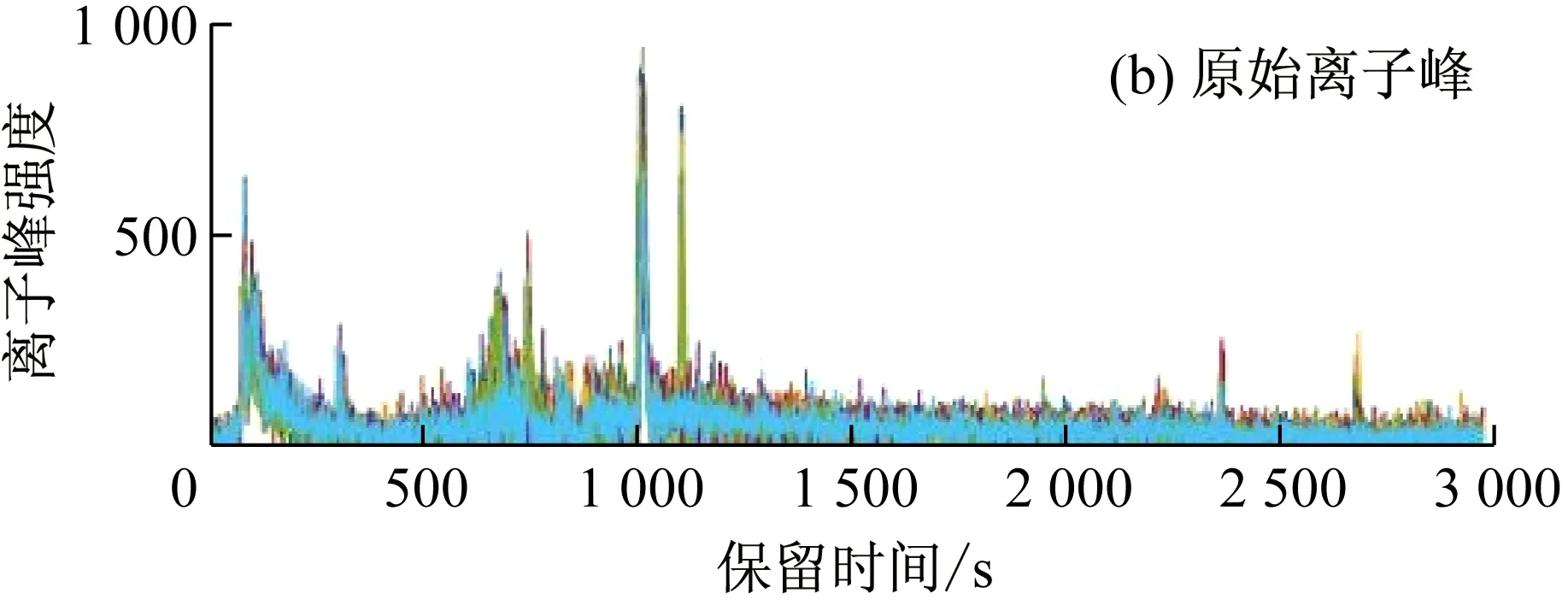
图5 峰对齐曲线(质量电荷比:380.125~380.625,样本数:20)
2.1 积聚峰的样本数目
由于样本噪声及样本间差异,多个样本都能对齐的离子峰有更高的可能性对应于小分子化合物,表1列出了不同质量电荷比下对齐的离子峰样本数(说明:质量电荷为780.125~780.625的20个样本中的12没有检测出峰)。
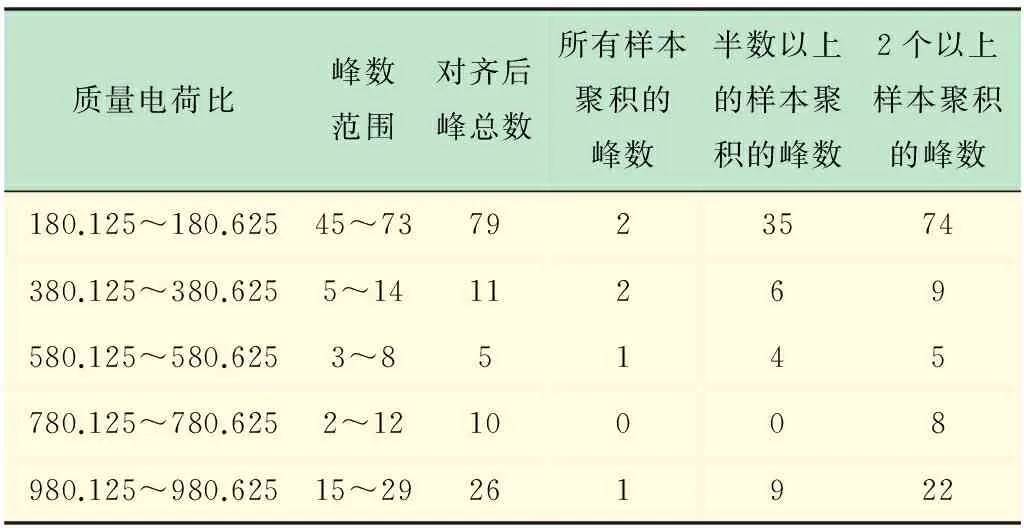
表1 对齐的离子峰样本数表(20个样本)
2.2 离子峰再识别
在峰对齐曲线中,将聚积在同一保留时间段上的峰为同一个峰。此外,那些只有一个样本所表现出来的峰应该是该样本的特性而并不体现多样本的共同对应的小分子化合物,因此对对齐后的峰进行进一步过滤,删除单样本峰,最终得到可能对应小分子化合物的离子峰。
3 结 论
LC/MS数据离子峰对齐是一个具有挑战的问题,主要的难度包括:峰检测、峰整合、降噪和标准化等[15]。流行的离子峰数据对齐方法,如XCMS(https://xcmsonline.scripps.edu/landing_page.php?pgcontent=mainPage),MetaboAnalyst(http://www.metaboanalyst.ca/)和MetAlign(https://www.wur.nl/en/show/MetAlign-1.htm)等,往往需要经过数据中心化、移去加合物、数据降噪、峰检测、峰整合、窗口选择等复杂的步骤,造成方法结构复杂、时间复杂度很高。本文提出的方法是一种快速计算LC/MS数据离子峰对齐的方法,该方法具有以下特点:
(1) 结构简单。本方法只包含3个模块:数据预处理、峰识别和峰对齐。
(2) 时间复杂度低。数据预处理阶段时间复杂度为kmst(其中:m是质量电荷比数量;s是样本数;t是保留时间点数;k是一个常数);峰检测阶段的时间复杂度为k1mst+k2msp,其中:p是候选峰数且p≪t,因此本阶段时间复杂度依然为kmst;峰对齐阶段的时间复杂度为kms2p2,由于p≪t,当样本数目不大时,kms2p2 (3) 参数依赖少。本方法使用参数4个(已内置于算法中,不需要用户选择):在数据处理阶段选择质量电荷比的步长值为0.25;在降噪阶段选择小波去噪及选择相应参数;在峰检测阶段使用合并参数MNP,本方法中选取经验值7作为域值;在峰过滤阶段以累积分布密度≥95%作为域值过滤候选峰。 [1] Daviss B. Growing pains for metabolomics [J]. Scientist, 2005, 19: 25-28. [2] Fiehn O, Kopka J, Dormann P,etal. Metabolite profiling for plant functional genomics [J]. Nat Biotechnol, 2000, 18: 1157-1161. [3] Wandy J, Daly R, Breitling R,etal. Incorporating peak grouping information for alignment of multiple liquid chromatography-mass spectrometry datasets [J]. Bioinformatics, 2015, 31: 1999-2006. [4] Smith R, Ventura D, Prince J T. LC-MS alignment in theory and practice: a comprehensive algorithmic review [J]. Brief Bioinform, 2015, 16: 104-17. [5] Tautenhahn R, Bottcher C, Neumann S. Highly sensitive feature detection for high resolution LC/MS [J]. BMC Bioinformatics, 2008, 9: 504. [6] Zhou B, Xiao J F, Tuli L,etal. LC-MS-based metabolomics [J]. Mol Biosyst, 2012, 8: 470-481. [7] Aberg K M, Alm E, Torgrip R J. The correspondence problem for metabonomics datasets [J]. Anal Bioanal Chem, 2009, 394: 151-162. [8] Hoffmann N, Keck M, Neuweger H,etal. Combining peak- and chromatogram-based retention time alignment algorithms for multiple chromatography-mass spectrometry datasets [J]. BMC Bioinformatics, 2012, 13: 214. [9] Lange E, Tautenhahn R, Neumann S,etal. Critical assessment of alignment procedures for LC-MS proteomics and metabolomics measurements [J]. BMC Bioinformatics, 2008, 9: 375. [10] Smith C A, Want E J, O'maille G,etal. XCMS: Processing mass spectrometry data for metabolite profiling using Nonlinear peak alignment, matching, and identification [J]. Analytical Chemistry, 2006, 78: 779-787. [11] Azizan K A, Ibrahim S, Ghani N H A,etal. LC-MS Based Metabolomics Analysis to Identify Potential Allelochemicals in Wedelia trilobata [J]. Records of Natural Products, 2016, 10: 788-793. [12] Zhang W, Zhao P X. Quality evaluation of extracted ion chromatograms and chromatographic peaks in liquid chromatography/mass spectrometry-based metabolomics data [J]. BMC Bioinformatics, 2014, 15(Suppl 11): S5. [13] Cappadona S, Levander F, Jansson M,etal. Wavelet-based method for noise characterization and rejection in high-performance liquid chromatography coupled to mass spectrometry [J]. Anal Chem, 2008, 80: 4960-4968. [14] Zhang J, Gonzalez E, Hestilow T,etal. Review of peak detection algorithms in liquid-chromatography-mass spectrometry [J]. Curr Genomics, 2009, 10: 388-401. [15] Zhang X, Asara J M, Adamec J,etal. Data pre-processing in liquid chromatography-mass spectrometry-based proteomics [J]. Bioinformatics, 2005, 21: 4054-4059. QuickPeakAlignmentAlgorithmforLC/MS-basedData SUNXiaohan (School of Security and Informatization, Weinan Normal University, Weinan 714000, Shaanxi, China) Liquid chromatography-mass spectrometry (LC/MS) is a technique combining the physical separation and mass analysis. This technique is wisely applied in the metabolomics studies sinceit can detect endogenous metabolites. However, the output data are often accompanied with high noise, and the retention times of ion peaks are nonlinear among samples.There fore it is a necessary step to align the peaks among these samples. The available alignment methods on LC/MS data are not suitable to fast alignment of ion peaks be cause they usually have complex structures and too many parameters to be set. A novel algorithm is proposed to perform fast peak alignment, itincludes three modules: data preprocessing, peak detection and peak alignment. The algorithm is simple in structure, has no parameters to be set by users and low time complexity. liquid chromatography-mass spectrometry (LC/MS); peak alignment; metabolic profile TP 311 A 1006-7167(2017)11-0020-04 2017-03-23 国家自然科学基金面上项目(61571341);中国国家留学基金资助项目(210508615092);陕西省自然科学基金(2017JM6036);渭南师范学院重点项目(16YKP002) 孙萧寒(1979-),女,陕西耀县人,副教授,现主要从事生物信息计算研究。 Tel.:15319118920; E-mail:sxhjpj@sina.com

