钢筋石笼串体稳定性试验研究

胡海松 伍学文 柳 滔

(三峡大学 水利与环境学院， 湖北 宜昌 443002)

钢筋石笼串体稳定性试验研究

胡海松 伍学文 柳 滔

(三峡大学 水利与环境学院， 湖北 宜昌 443002)

钢筋石笼串体是截流工程施工中较为重要的人工材料，研究钢筋石笼串体综合稳定性系数对其在实际应用中尤为重要．本文主要通过物理模型试验，得出钢筋石笼串体综合稳定系数范围，同时通过对伊兹巴斯公式综合稳定系数进行修正引入综合稳定折算系数α，拟合出钢筋石笼串体起动流速公式，为类似工程研究提供重要的参考依据．

截流； 钢筋石笼串体； 综合稳定性系数； 起动流速

1 研究背景

在水利施工中解决截流难度和提高截流效率一直是众多学者研究的关键问题，而钢筋石笼是将编制好的钢筋笼填充天然的石块构成的整体，在一定程度上增大了块体的重量，并具有较好的透水性和柔性特点，其抗冲能力明显高于单独石料及其他抛投材料，已在截流工程、护岸工程中得到了广泛的应用．目前，已经有学者针对钢筋石笼的截流研究做了大量的工作，如肖焕雄[1]对立堵截流抛石立径计算进行研究；李学海[2]的钢筋石笼的稳定性及其计算方法；孙东坡[3]对截流龙口水力特性与截流的试验进行了研究；叶恩立[4]的钢筋石笼起动流速试验与流场结构数值分析，黄国兵[5]等以截流块体稳定影响因素而推导出实用计算公式．然而到目前为止，针对钢筋石笼串体稳定性研究的理论成果并不是很多．因此，进行钢筋石笼串体的稳定性研究具有一定的学术价值和实用意义．

2 问题提出与分析

本文把钢筋石笼串体作为影响因素，通过一系列的起动流速试验，对伊兹巴斯公式综合稳定系数作出一定的修正，引入综合稳定折算系数α，转化为钢筋石笼串体截流块体的计算公式，期待为钢筋石笼串体在截流工程中的应用提供理论指导．

3 钢筋石笼串体稳定性试验

3.1 试验设计

试验在1∶50比尺的水槽模型中进行，其宽度为0.5 m，高度为0.8 m，长度为15 m，左右以及底部均采用加厚玻璃制作，便于试验观察，并通过流量控制仪器调节水槽内部的流量、流速、水位以满足试验的需要．

图1 试验水槽模型

试验工况：本次试验研究正六面体形状的钢筋石笼，在正六面体钢筋笼内装入不同级配的石子，使石笼的重量存在差异，分别设置2个、3个、4个、5个一串4组，每组设置2 cm、2.5 cm、3.0 cm、3.5 cm、4.0 cm边长的5种尺寸，一共20组工况，进而讨论钢筋石笼串体稳定性试验研究．

3.2 试验结果

本文指出钢筋石笼串体试验都是垂直于水流方向摆放，并且串体均是只发生水平滑动，不发生滚动和翻转．本试验采用多普勒超声流速仪测量钢筋石笼串体截面的平均流速，截面取左中右3条垂线，垂线采用三点法，截面流速取9点的平均值．钢筋石笼串体抗冲起动流速的试验结果见表1．

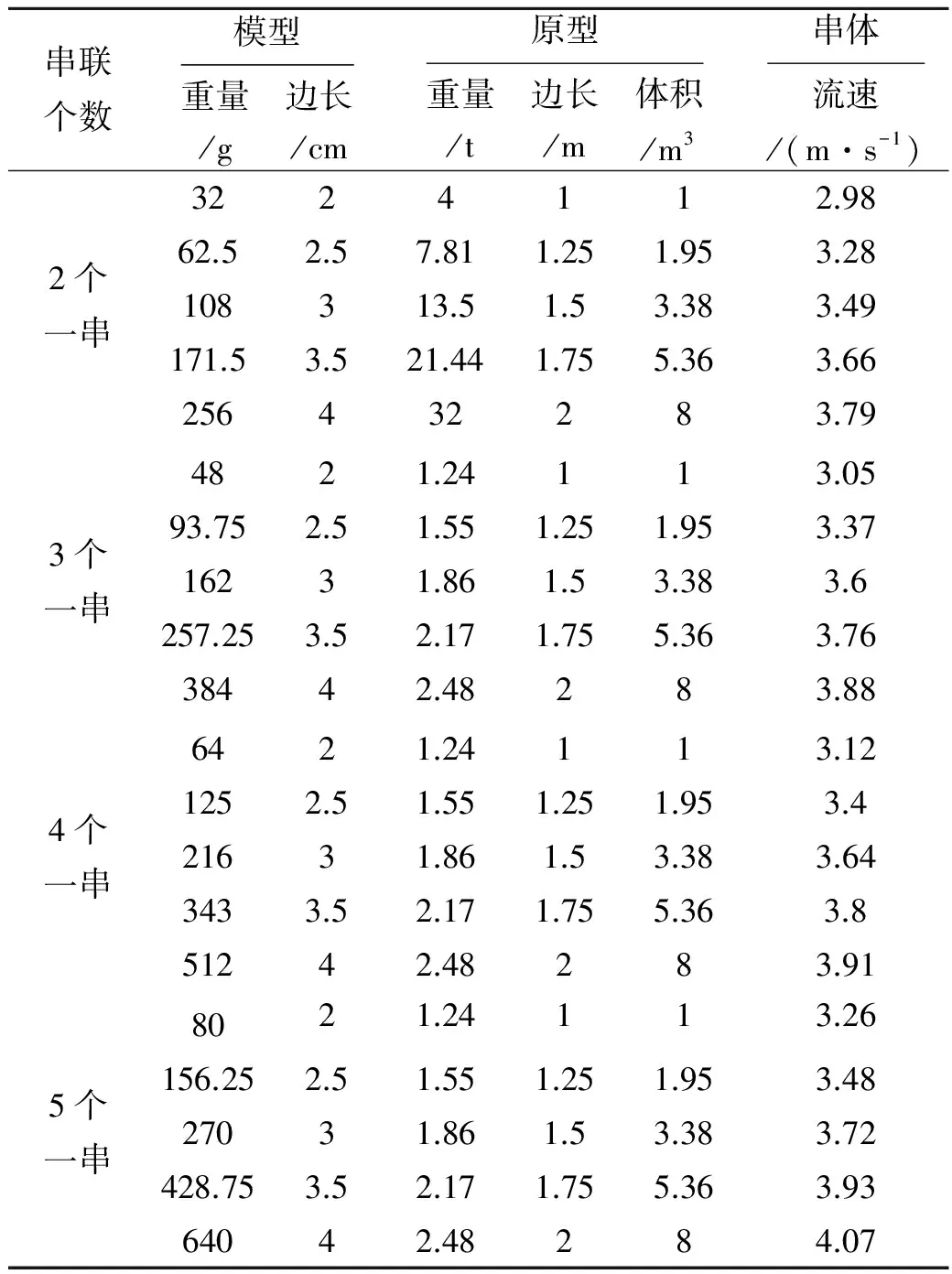
表1 正六面体钢筋石笼串体流速测量结果

3.3 钢筋石笼串体综合稳定性系数计算

试验结果表明，钢筋石笼串体综合稳定系数变化范围为0.543～0.661．钢筋石笼串体综合稳定系数随着串体个数的增加而增大，且在串联个数相同的情况下，串体的抗冲流速随着串联单体重量的增加而变大，其综合稳定系数值随着串联单体重量的增加而逐渐减小，如图2所示．

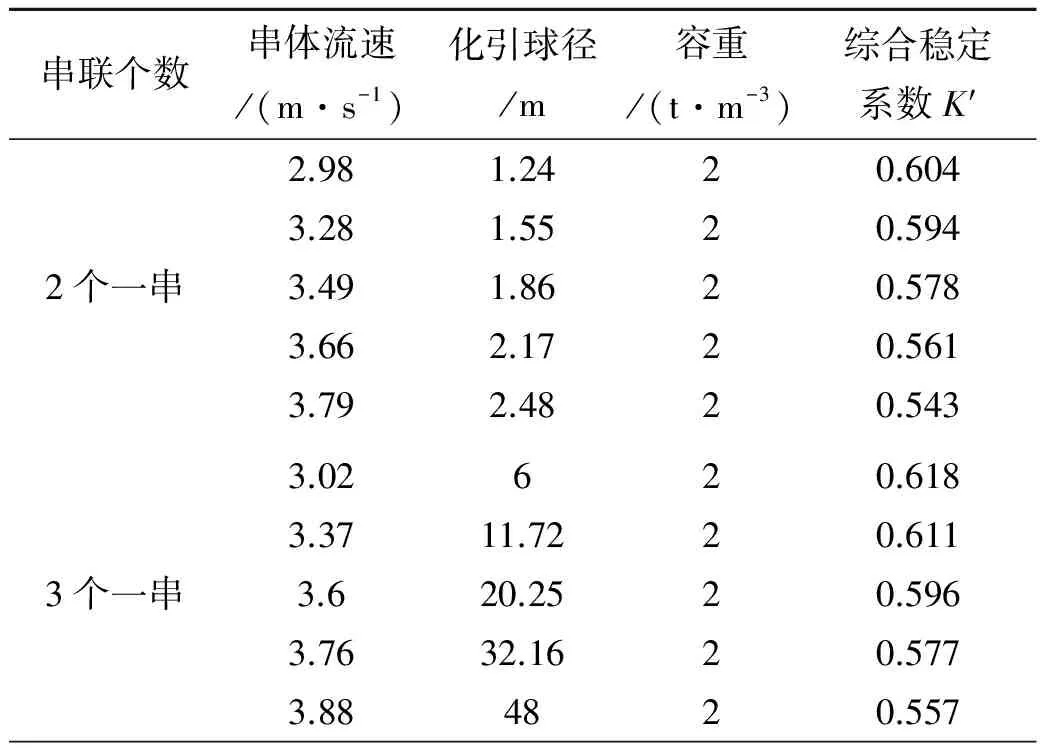
表2 正六面体钢筋石笼串体综合稳定系数K′计算结果

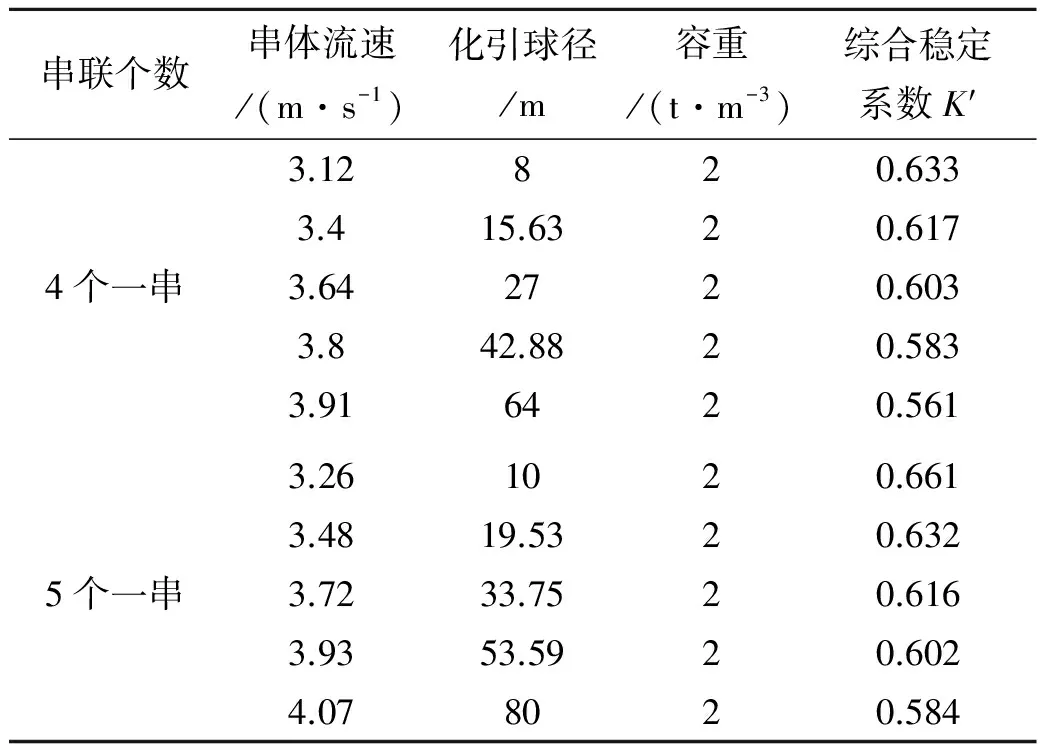
续表2 正六面体钢筋石笼串体综合稳定系数K′计算结果

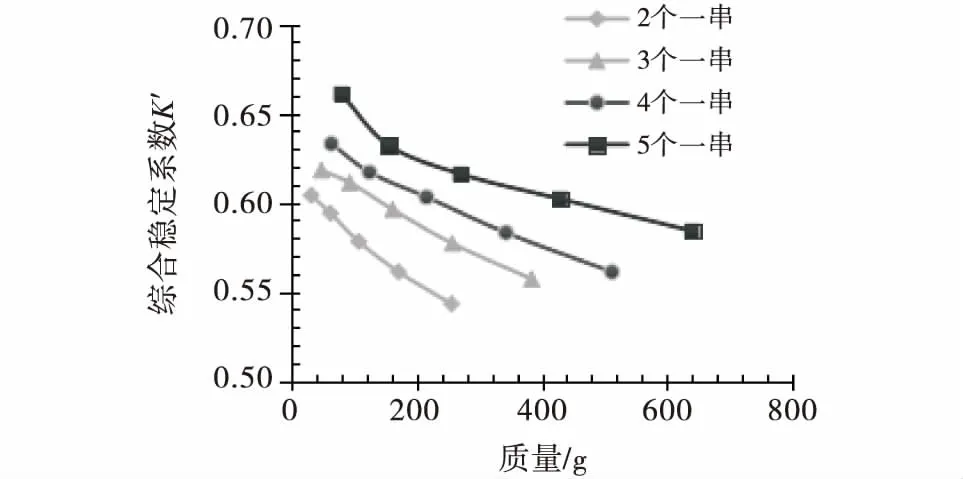
图2 正六面体钢筋石笼串体对综合稳定系数K′影响

4 钢筋石笼串体稳定计算公式的拟合与验证

4.1 钢筋石笼串体的稳定计算公式拟合

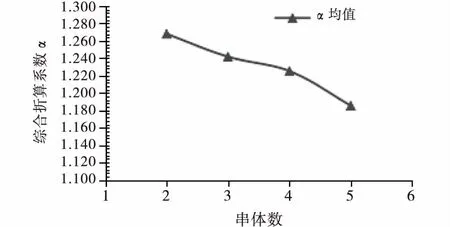
图3 正六面体钢筋石笼串体综合稳定折算系数α计算结果

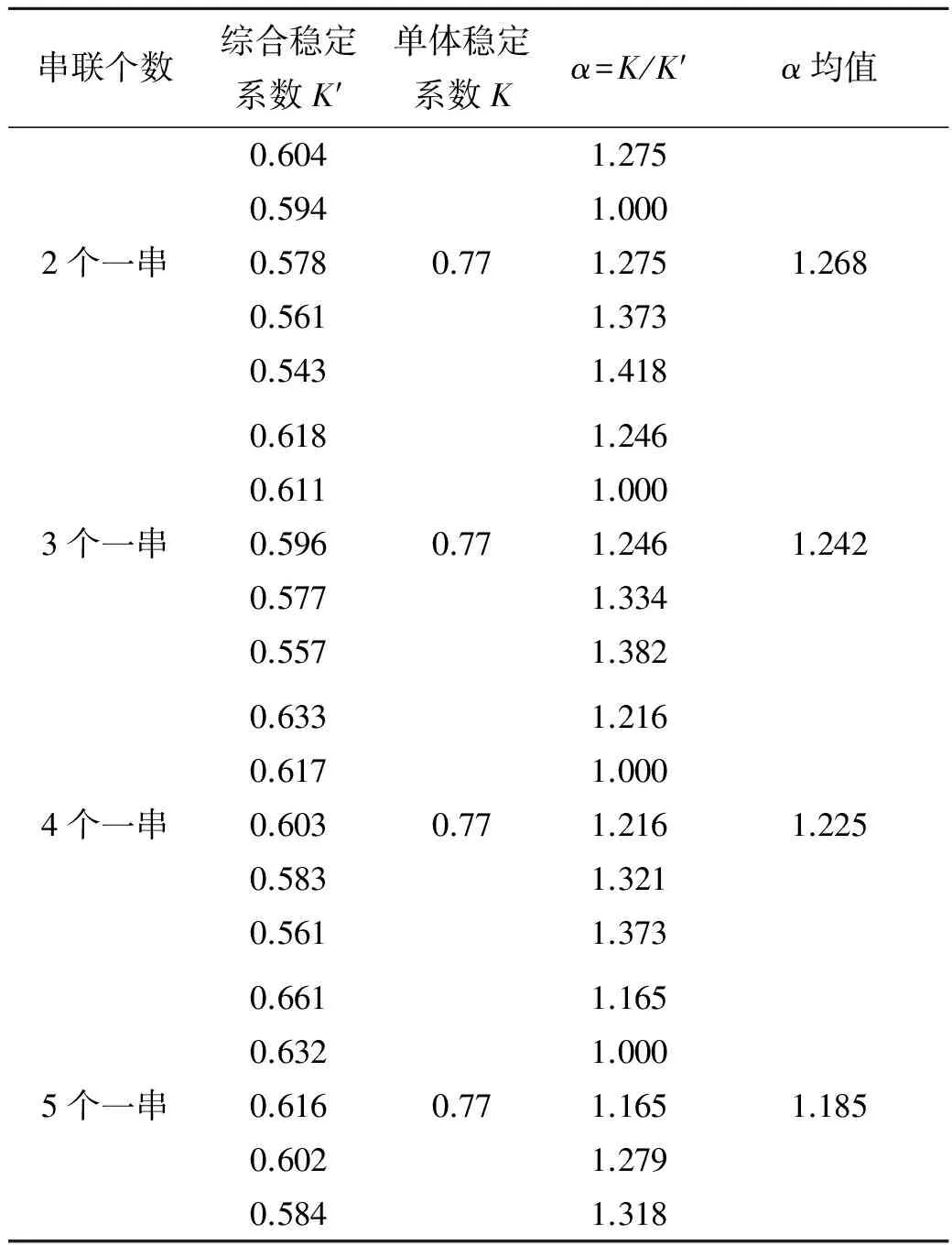
串联个数综合稳定系数K′单体稳定系数Kα=K/K′α均值2个一串0．6041．2750．5941．0000．5780．771．2751．2680．5611．3730．5431．4183个一串0．6181．2460．6111．0000．5960．771．2461．2420．5771．3340．5571．3824个一串0．6331．2160．6171．0000．6030．771．2161．2250．5831．3210．5611．3735个一串0．6611．1650．6321．0000．6160．771．1651．1850．6021．2790．5841．318

4.2 钢筋石笼串体的稳定计算公式的验证

为验证公式(2)的准确性，本文又进行了验证试验，针对串体个数不同的钢筋石笼，在试验条件相同的情况下进行验证试验．将试验测得的钢筋石笼串体起动流速与依据式(2)计算所得的起动流速进行对比分析，结果见表4，计算值与实测值的对比如图4所示．

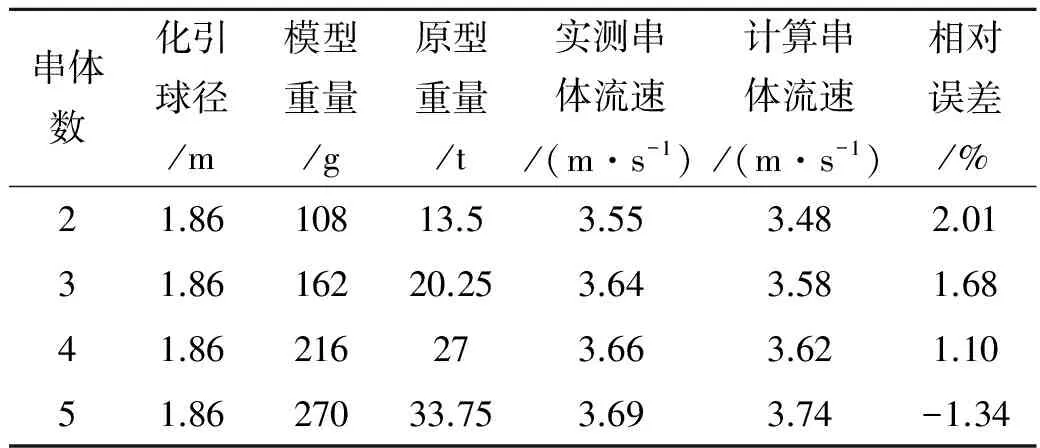
表4 钢筋石笼串体起动流速试验验证计算结果

图4 钢筋石笼串体起动流速计算值与试验值比较

由表4和图4可知，用本文拟合钢筋石笼串体公式计算的起动流速值与试验实测的起动流速值基本吻合，误差在1.10%～2.01%之间，满足实验室误差[6]精度要求．

5 结 论

本文通过对钢筋石笼串体的稳定性起动流速试验数据研究分析，得出如下结论：

1)串体个数一定，随着钢筋石笼串体质量的增加起流速也随之增加，稳定性越好．

2)钢筋石笼串体综合稳定系数K′变化范围为0.543～0.661，它随钢筋石笼串体质量的增大而减小，同时随串联个数的增加而增加．

3)在伊兹巴斯公式的基础上，引入了综合稳定折算系数α，拟合出钢筋石笼串体综合稳定系数起动流速新的计算公式，经试验验证该公式计算精度较好，具有一定可靠性，对实际工程应用有一定的参考价值．

[1] 肖焕雄．立堵截流抛石立径计算研究[J]．水电站设计，2000，1(3)：1-7．

[2] 李学海，程子兵，汪世鹏，等．钢筋石笼的稳定性及其计算方法[J]．长江科学院院报，2013，30(8)：31-36．

[3] 叶恩立，周宜红，肖焕雄，等．钢筋石笼启动流速试验与流场结构数模分析[J]．天津大学学报，2014，47(2)：108-115．

[4] 孙东坡，赵若鼎，严 阔，等．立堵截流龙口水利特性与截流难度的试验研究[J]．中国农村水利水电，2013(5)：122-125．

[5] 黄国兵，李学海，程子兵，等．截流块体稳定影响因素及实用计算公式[J]．长江科学院院报，2013，30(8)：25-30．

[6] 肖焕雄．施工水力学[M]．北京：水利电力出版社，1992．

[7] 杨旭武．实验室误差原理与数据处理[M]．北京：科技出版社，2009．

ExperimentalStudyofReinforcedGabionStringBodyStability

Hu Haisong Wu Xuewen Liu Tao

(College of Hydraulic & Environmental Engineering， China Three Gorges Univ.，Yichang 443002， China)

The reinforced gabion is one of the most important artificial materials in the construction of the river closure project. It is very important to study the comprehensive stability coefficient of the reinforced gabion. Through the physical model test, the reinforced gabion body comprehensive stability coefficient range is obtained. Meanwhile, based on the comprehensive stability coefficient, S. V. lsbash formula modification is introduced into the integrated stable conversion coefficient, fitting out the starting velocity of reinforced gabion string body, so as to provide important reference for similar projects.

river closure； reinforced gabion string body; comprehensive stability coefficient; starting velocity

10.13393/j.cnki.issn.1672-948X.2017.05.012

2017-03-10

水利部公益性行业科研专项项目(2014401027)

胡海松(1992-)，男，硕士研究生，主要从事水力学及河流动力学研究，E-mail：2369577695@qq.com

TV131

A

1672-948X(2017)05-0059-04

[责任编辑王迎春]