一类随机切换模糊时滞系统的镇定研究
李梁杰, 范立南, 杨 红
(沈阳大学 信息工程学院, 辽宁 沈阳 110044)
一类随机切换模糊时滞系统的镇定研究
李梁杰, 范立南, 杨 红
(沈阳大学 信息工程学院, 辽宁 沈阳 110044)
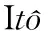
模糊系统; 随机; 时滞; 切换系统; 切换律
现代工业生产流程中碰到的各种控制问题十分复杂,被控制的系统包含了许多连续时间动态系统、离散事件动态系统,以及彼此之间的相互耦合作用,具有非常明显的“混杂”特性,这样的系统被称为混杂系统.典型的切换系统是由一组连续(或离散)的时间子系统和作用在其中合适的切换规则组合而成的,其中子系统是切换系统的连续动态部分,切换规则是切换系统的逻辑、决策部分,表现形式为离散动态.整体切换系统的运行状况受控于这条切换规则,这条规则也称为切换律或切换信号,一般情况下它是一个依赖于状态或时间的分段常值函数.子系统之间的切换表示离散时间动态,每个子系统对应着离散变量的一个取值.切换系统的性质不是子系统各自性质的简单叠加,而是与切换律紧密联系的,切换律设计对于切换系统而言是非常重要的.切换系统是混杂动态系统的一种重要简化模型,具有很强的建模通用性,子系统是T-S模糊模型的切换模糊系统,简称为T-S切换模糊系统,该系统是目前混杂系统的一个研究热点[1-5].沟通模糊系统和线性系统联系的桥梁之一就是T-S模糊动态模型,该系统的出现使得模糊系统得到了极大的丰富,拓宽了线性系统和非线性系统的有关理论稳定性研究,文献[6-8]基于此类系统的研究具有相当的代表性,并已在大量的现实生活问题中得到了应用,获得了相当多的社会和经济效益.
随机系统是含有大量不同随机变量的系统,其包含了内部随机参数、元器件自带误差及运行时产生的噪声、外部随机干扰等.在系统中引起不确定性的原因是随机性的存在,因此复杂系统中引起不确定性的因素是大量存在的且无法避免,则原来按照确定性控制理论设计的控制行为就会偏离预定的设计要求,随着时间变量的增加,随机偏差量就会积累到最终控制器达不到理想的设计目标[9].
模糊切换系统和随机系统在各自领域都获得了巨大的发展.文献[10]分析了各类不确定切换模糊时滞系统的可靠控制问题.针对典型的混杂系统,重新设计使系统渐近稳定的状态反馈控制器及切换律,以及在系统状态不可观测情况下,进行重构系统状态,设计合适的模糊控制器等方面都取得了很大的成果[11-14].文献[15]采用了含有随机因素的Lyapunov稳定性理论,对T-S模糊随机时滞系统的鲁棒控制进行研究,但是在分析Lypaunov泛函时并没有用模型变换的方法.目前含有随机因素的模糊切换系统的研究成果还比较有限,文献[16]研究了包含有随机元素的T-S模糊切换系统的均方镇定问题,但该系统并没有考虑含有时滞时的情况.而本文则是基于T-S模糊时滞随机切换系统,研究了模糊时滞随机切换系统的镇定问题.提出了新的包含有时滞的随机模糊切换控制理论方法,进一步丰富和完善了现有的切换系统控制理论,拓宽了对复杂系统的控制研究.本文采用多Lyapunov函数方法,对不确定模糊随机时滞系统设计状态反馈控制器,当系统运行过程中发生了严重不稳定状况时,设计的控制器进行切换使系统快速稳定.
1 问题描述
有Nσ(t)个模糊规则带有时滞的随机切换模糊系统模型如下:
式中

第i个带有时滞的随机切换模糊系统的数学模型如下:
第i个带有时滞的随机切换模糊系统全局数学模型如下:
式中
有

选择的前件变量和式(1)系统是相同的,根据模糊系统中的平行分布补偿(parallel distributed compensation,PDC)控制器,设计出相应的切换PDC控制器,即
l=1,2,…,Nii=1,2,…,m.
那么式(6)控制器的全局模型如下
则第i个带有时滞的随机切换模糊系统的闭环全局数学模型为:
假设以下参数不确定项是范数有界的,而且满足
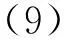

以上是随机模糊切换时滞系统的数学模型描述,下面给出本文的定理1,定理1采用矩阵不等式,对切换系统进行数学模型上的理论推导.
定理1 多Lyapunov函数方法
假设存在两个非正或非负常数βiα,两个正定矩阵Pi、Qi,若以下矩阵不等式
成立,则设计的切换律为
使得式(8)闭环系统在式(7)切换控制器下是渐近稳定的,即保证了闭环系统是相对稳定的.
证明 假设βi α同为非负,则对于∀x∈Rn{0},必有一个i∈M,使得
xT(t)(Pi-Pα)x(t)≥0,∀α∈M,
存在矩阵不等式
令
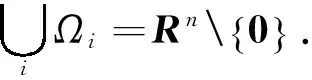

(12)
则可以获得矩阵不等式
当以上公式成立时,有dVilt;0,则式(8)闭环系统是渐近稳定的.
设计切换律为
定理1中的矩阵不等式只是切换系统数学模型上的理论推导,计算十分复杂,为了LMI可解,方便切换控制系统的应用和推广,由定理1产生定理2,定理2作了相应的变换,得到了MATLAB可解的LMI形式.
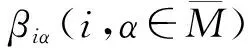

系统的切换信号设计为
2 仿真实例
文献[17]构造了1个切换混沌系统,其子系统是2个不同的混沌系统,不同的混沌系统之间通过操作开关来实现彼此切换,该类切换系统具有极大的操作灵活性.
此类混沌系统方程表示如下:
安全性、保密性是现代同步通信研究中一个非常重要的性能,在通信领域中采用多关联系统切换混沌同步的通讯系统,可以极大地加强混沌同步保密通信的安全时效性能,同时,这类切换系统在其他领域也具有广泛的潜在应用价值.
建立的随机切换模糊时滞系统模型如下:
式中
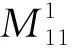
求解式(16)LMI,可以得到
取初始条件为x(0)=[-10;10].图1为整体随机切换模糊时滞系统的状态响应曲线,图2、图3分别为随机切换模糊时滞系统的子系统1和子系统2的状态曲线.可以根据对比仿真例子看出,如果子系统1和子系统2的收敛效果都各自达不到要求时,设计恰当的切换信号能让整个随机切换模糊时滞系统状态获得很好的稳定性能,实现理想的控制效果.

图1 随机切换模糊时滞系统的状态响应曲线

图2 子系统1的状态响应曲线Fig.2 State response curve of sub-system 1

图3 子系统2的状态响应曲线Fig.3 State response curve of sub-system 2

图4 随机切换模糊时滞系统的状态响应曲线
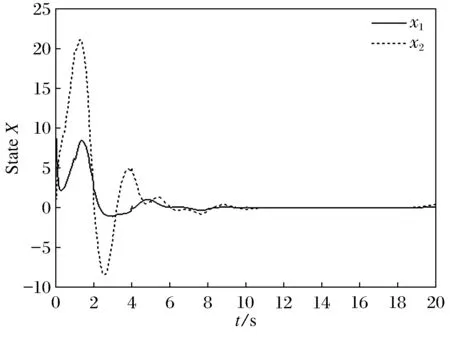
图5 随机模糊时滞子系统2的状态响应曲线
利用文献[15]中的模糊随机时滞方法进行了仿真.取初始条件为x(0)=[15;-4].
改变初始条件,采用文献[15]中的方法.图4为添加有切换模块的模糊随机时滞系统的状态响应曲线,图5为随机模糊时滞子系统2的状态曲线.由以上仿真图可看出,当其子系统2的超调量较大,收敛效果不是很好时,加上设计的切换信号之后,整体的随机模糊时滞系统状态获得了很好的收敛性,图4体现了本文方法的优势.
3 结 论
本文研究了不确定随机切换模糊时滞系统的控制问题.这类模型结合了随机系统控制和切换模糊控制各自的优势,对混杂系统具有很好的控制效果,随机切换模糊时滞系统的所有子系统均为包含有随机因素的模糊时滞系统.基于多Lyapunov函数方法,稳定性条件以可解的LMI形式给出,设计出新的切换控制策略,当子系统出现较大的波动时,可以使整个随机切换模糊时滞系统获得理想的稳定性.最后,通过两组仿真实验验证了此方法的可行性和有效性.
[ 1 ] TANAKA K,WANG H. A descriptor system approach to fuzzy control system design via fuzzy Lyapunov function[J]. IEEE Trans-actions on Fuzzy Systems, 2007,15(3):333-341.
[ 2 ] LIU M,SHI P,ZHANGL,et al. Fault-tolerant control for nonlinear Markovian jump systems via proportional and derivative sliding mode observer technique[J]. IEEE Transactions on Circuits and Systems Ⅰ: Regular Papers, 2011,58(11):2755-2764.
[ 3 ] XIA Z L. Delay-dependent generalized H2control for discrete-time T-S fuzzy systems based on a switching fuzzy model and piecewise Lyapunov function[C]∥Fifth International Conference on Fuzzy Systems and Knowledge Discovery, 2008:243-247.
[ 4 ] 李华. 一类带有时滞的切换模糊系统的鲁棒控制设计[D]. 沈阳:东北大学, 2012:21-30.
LI H. Robust control design for a class of switched fuzzy systems with time-delay[D]. Shenyang: Northeastern University, 2012:21-30.
[ 5 ] SALA A,ARINO C. Asymptotically necessary and sufficient conditions for stability and performance in fuzzy control: Applications of Polya’s theorem[J]. Fuzzy Sets and Systems, 2007,158(24):2671-2686.
[ 6 ] WAND W J,SUN C H. Relaxedstability and stabilization conditions for a T-S fuzzy discrete system[J]. Fuzzy Sets and Systems, 2005,156(2):208-225.
[ 7 ] LIU Y G,ZHAO S W. T-S model-based impulsive control for chaotic systems and its application[J]. Mathematics and Computers in Simulation, 2011,81(11):2507-2516.
[ 8 ] 齐丽,杨俊友. 基于观测器的不确定T-S模糊系统鲁棒镇定[J]. 控制理论与应用, 2010,27(5):627-630.
QI L,YANG J Y. Observer-based robust stabilization of uncertain T-S fuzzy systems[J]. Control Theory amp; Applications, 2010,27(5):627-630.
[ 9 ] 王芬. 不确定随机时滞系统的稳定性[D]. 武汉:武汉科技大学, 2006:10-21.
WANG F. Stability of uncertain stochastic systems with time delays[D]. Wuhan: University of Science and Technology Wuhan, 2006:10-21.
[10] 吴金男,张乐. 一类不确定切换模糊时滞系统的可靠控制[J]. 沈阳大学学报(自然科学版), 2014,26(1):55-59.
WU J N,ZHANG L. Reliable control for a class of uncertain switched fuzzy time-delay[J]. Journal of Shenyang University (Natural Science), 2014,26(1):55-59.
[11] 杨月全,邓林,姜建妹,等. 一类时滞不确定切换T-S模糊系统的稳定性分析[J]. 东南大学学报(自然科学版), 2010,40(1):127-130.
YANG Y Q,DENG L,JIANG J M,et al. Stability analysis of s class of uncertain switched T-S fuzzy systems with time-delay[J]. Journal of Northeastern University(Natural Science), 2010 40(1):127-130.
[12] 刘毅,冯佳昕,赵军. 一类不确定离散切换模糊时滞系统的鲁棒输出反馈控制[J]. 东北大学学报(自然科学版), 2009,30(1):13-16.
LIU Y,FENG J X,ZHAO J. Robust output-feedback control for a class of uncertain discrete switched fuzzy systems with time-delay[J]. Journal of Northeastern University(Natural Science), 2009,30(1):13-16.
[13] 张乐,杨红,井元伟. 一类不确定切换模糊系统的鲁棒可靠自适应控制[J]. 东北大学学报(自然科学版), 2008,29(9):1228-1231.
ZHANG L,YANG H,JING Y W. Robust and reliable adaptive control of a class of uncertain switched[J]. Journal of Northeastern University(Natural Science), 2008,29(9):1228-1231.
[14] 杨红,李猛,宋健,等. 基于T-S模型的模糊时滞系统混杂输出控制[J]. 沈阳大学学报(自然科学版), 2016,1(28):41-44.
YANG H,LI M,SONG J,et al. Output hybrid control for a class of fuzzy time-delay systems based on T-S model[J]. Journal of Shenyang University (Natural Science), 2016,1(28):41-44.
[15] 鲁叶,彭世国. T-S模糊随机时滞系统的鲁棒控制[J]. 广东工业大学学报, 2013,30(1):68-71.
LU Y,PENG S G. Robust control of T-S fuzzy stochastic system with time-delay[J]. Journal of Guangdong University of Technology, 2013,30(1):68-71.
[16] 张乐,郭春鹏,关忱,等. 基于T-S模型的随机切换模糊系统的稳定性研究[J]. 沈阳大学学报(自然科学版), 2017,29(2):107-112.
ZHANG L,GUO C P,GUAN C,et al. Stabilization analysis for a class of stochastic switched fuzzy systems based on T-S model[J]. Journal of Shenyang University(Natural Science), 2017,29(2):107-112.
[17] 王忠林,刘滨,王树斌. 一个切换混沌系统的设计与实现[J]. 中国海洋大学学报, 2009,39(3):509-512.
WANG Z L,LIU B,WANG S B. Design and implementation of a switchable chaotic system[J]. Periodical of Ocean University of China, 2009,39(3):509-512.
【责任编辑:肖景魁】
StabilizationforaClassofStochasticSwitchedFuzzySystemswithTime-Delay
LiLiangjie,FanLinan,YangHong
(School of Information Engineering, Shenyang University, Shenyang 110044, China)

fuzzy systems; stochastic; time delay; switched system; switching law
TP 273
A
2017-09-18
国家自然科学基金资助项目(61603261); 沈阳市科技计划资助项目(17-175-3-00).
李梁杰(1993-),男,山西阳泉人,沈阳大学硕士研究生; 范立南(1964-),男,辽宁沈阳人,沈阳大学教授,博士.
2095-5456(2017)06-0466-07

