基于GWR的住宅地价相对修正方法研究——以深圳市为例

胡 炜，刘永学，林勇军

（1.深圳市规划国土发展研究中心，广东 深圳 518040；2.国土资源部城市土地资源监测与仿真重点实验室，广东 深圳 518034；3.南京大学地理与海洋科学学院，江苏 南京 210023）

基于GWR的住宅地价相对修正方法研究
——以深圳市为例

胡 炜1，2，刘永学2，3，林勇军1，2

（1.深圳市规划国土发展研究中心，广东 深圳 518040；2.国土资源部城市土地资源监测与仿真重点实验室，广东 深圳 518034；3.南京大学地理与海洋科学学院，江苏 南京 210023）

研究目的：提出一种适用于地产市场活跃地区的住宅地价相对修正方法，解决传统市场比较法过分依赖估价师经验的问题。研究方法：运用GWR模型，量化影响因素对住宅地价作用的空间分异规律，确定影响因素单位变化对应的地价修正百分比；运用空间单元相似度评价方法，自下而上生成住宅地价修正分区。研究结果：从GWR模型原理出发，建立了基于客观数据的修正公式；构建了从回归模型构建到修正分区建立，再到地价修正的完整技术路线；研究提出的修正方法经真实数据检验取得了较好的效果。研究结论：本文构建的住宅地价相对修正方法在估价工作中具有实操可行性；地价修正精度与GWR模型构建精度正相关；该方法更加适用于具备高密度地价样本点的地产市场活跃地区。

土地经济；住宅地价；地价修正；GWR；深圳市

1 引言

根据《城镇土地估价规程》（GB/T 18508-2014），地价评估的基本方法主要有市场比较法、收益还原法、剩余法和成本逼近法4种[1]。市场比较法通过选取与待估宗地在同一供需圈内的3个（含3个）以上比较实例，通过对比较实例的成交价格进行比较、修正得到待估宗地的评估价格。在地产市场活跃、有充足可比实例的地区，通常为估价的首选方法[2]。收益还原法通过选取一定的还原利率，将未来若干年中预期从土地上获取的纯收益折算为评估基准日时的收益总和，即为地价，适用于商业等有现实收益或潜在收益的土地。剩余法通过从开发完成后的房地总价中扣除所需花费的建筑成本、相关税费、各类预付资本利息及开发利润等，剥离出土地价格，适用于具有投资开发或在开发潜力土地的估价。成本逼近法以取得和开发土地所耗费的各项费用之和为主要依据，加上一定的利润、利息、税费和土地增值收益来推算土地价格。该方法一般只适用于新开发土地或土地市场欠发育、交易实例少的地区。在上述4种方法中，只有市场比较法最适用于地产市场活跃地区的住宅地价评估。

市场比较法的使用中存在两个关键环节：同一供需圈的确定；待估对象与比较实例对比修正。对于前者，土地估价师一般根据经验确定“同一供需圈”的具体含义，选取空间和属性上较为接近的案例作为地价修正参考；对于后者，则需要借助地价影响因素修正系数表，将待估对象与对比案例在属性上的差异转换为地价百分比的差异进行累加修正，而该表往往借助专家打分法等经验方式确定。可见，目前市场比较法在实操过程中带有一定的主观性，估价结果的准确性一定程度上依赖于估价师的个人经验[3]。在地产市场活跃地区，影响因素与地价的关系已经充分体现在丰富的地价样本点中，因此可考虑借助地理统计模型对这种关系进行定量描述，为地价相对修正提供客观参考。

2 基于GWR的住宅地价相对修正方法

2.1 方法思路分析

土地是一种高度异质性的商品，对于这类商品的价格，学界常采用特征价格模型（Hedonic模型）进行描述。该模型最早由Court在1939年用来研究汽车的价格与汽车特征的关系，建立汽车产业的价格指数[4]。随着研究的深入和计算机技术的发展，特征价格模型逐渐在土地和房地产市场研究领域发挥着越来越重要的作用，产生了大量的研究成果[5-7]。特征价格模型将土地看做是属性特征（区位、交通、配套等）的集合[8]，消费者购买土地时实际上是在选择一个属性集，土地的价格可以看做是其内含属性特征复合的结果。为了描述土地属性和土地价格的关系，国内外学者发展了线性形式、对数形式、半对数形式等一系列函数模型[9]。虽然形式上有所不同，但上述模型均只能使用在统一的城市土地市场中，即土地属性对土地价格的贡献在研究范围内应保持一致，但多名学者研究表明，土地市场具有空间分割性的特点，即土地属性对价格的作用具有空间非平稳性[10-14]。在城市尺度下，土地市场往往需要被分割为若干个子市场，才能在子市场内部满足统一市场假设，进而使用特征价格模型。为了解决这一问题，地理加权回归模型（GWR）被引入地价研究领域[15-16]，该模型通过在每一样本点建立独立的回归方程以克服空间异质性问题。

理论上，在样本点足够丰富的情况下，可以在城市范围内建立土地价格与土地属性的GWR模型，只要给定待估宗地的属性，即可通过回归方程求出其价格，但该方法在实际操作中面临3个主要问题：土地价格会随着时间发生变化，尤其在中国当前的发展阶段，土地价格变化速度较快，而完善的GWR模型需要经过数据收集筛选、模型构建、模型检验及调校等诸多环节，难以实时更新；GWR模型难以在市域任何地区均保持较高精度，局部土地价格仍要以时空上相近比较实例作为锚定；该方法不属于《城镇土地估价规程》规定范围，在实际估价业务中无法使用。

因此，综合考虑科学性和实操性两方面因素，本文以特征价格模型为理论基础，借助GWR模型对市场比较法的两个关键环节（同一供需圈确定和对比修正）进行完善，建立一种基于GWR的住宅地价相对修正方法。

2.2 方法原理

由于影响因素对于地价的作用会随着空间位置的不同而不同，因此修正模型必须考虑这种作用的空间分异，较为可行的做法是引入GWR模型，该模型已被多次证明适用于不动产价格的解释。基于GWR模型的特征价格模型可以描述为：

式（1）中，yi为第i个地价点的价格，（ui，vi）为第i个地价点的空间坐标，βk（ui，vi）为第k个地价影响因素在i处的回归系数，xik为第k个地价影响因素在i处的取值，εi为回归残差[17]。

回归系数βk（ui，vi）的涵义为：第k个地价影响因素在i处每增加一个单位，地价增加的绝对数值。为了与市场比较法中的百分比修正保持一致，定义“校正回归系数”αk（ui，vi） =βk（ui，vi）/yi，αk（ui，vi）的涵义为：第k个地价影响因素在i处每增加一个单位，地价上升的百分比，相应的GWR模型公式可写作：

对于i和j两个地价点，若二者的空间位置较为接近以致可以忽略影响因素对地价作用的空间分异，可假设在yi和yj差异不大的情况下，则i点的地价可近似由j点的地价经下式修正得到：

根据式（3），将i作为待估地价点，j作为参考地价点，即可通过对比i、j的影响因素差异，由地价点j的价格修正得到地价点i的价格。

2.3 修正模型构建技术路线

根据模型原理可知，该修正模型的使用须满足以下条件：（1）两个地价点的空间位置较为接近，使得β0（ui，vi）和β0（uj，vj）取值相当，αk（ui，vi）和αk（uj，vj）（k= 1，2，3，…）取值相当；（2）参考案例点和待评估地价点在影响因素取值上的差异不能过大，避免yi和yj差异过大。

根据地理学第一定律，一个空间单元内的信息与其周围单元信息有相似性。若将市域空间划分为若干较小的子单元，在子单元内部进行地块间的修正，则较容易保证上述两个条件的成立，因此修正模型构建的技术路线为：（1）选取覆盖全市域，具备足够数量的地价点，获取同一时点的地价和影响因素信息建立GWR回归模型，内插得到常数项和各影响因素的β0和αk（k= 1，2，3，…）值栅格图。（2）设计覆盖城市地价待估区域的最小修正分区，统计每个修正分区内的β0平均值和αk平均值向量。（3）遍历所有修正分区，将满足以下条件的修正分区合并：①空间相邻；②两个修正分区的β0平均值差值和αk平均值向量差异小于相应阈值；③拟合并形成的新修正分区内部的各栅格αk值离散程度小于相应阈值。重新统计合并后修正分区内的β0平均值和αk平均值向量。（4）采用深度优先或广度优先次序重复进行步骤（3），直到所有可合并的修正分区均合并完成。

经过上述步骤，即得到最终估价修正分区，每个修正分区对应一个αk值向量，可支持分区内部属性相似地块的价格相互修正。

3 实证分析

3.1 研究区与数据

3.1.1 研究区 深圳市位于广东省南部，北邻东莞、惠州，南接香港，西临珠江口，土地面积1997 km2，常住人口1078万人（2014年末），是华南地区的特大城市。全市下辖10个（新）区，其中福田、罗湖、南山、盐田4区为原特区内部分，也是土地利用总体规划（2006—2020年）确定的中心城区范围。全市地貌以山地丘陵为主，山体多为500—700 m的低山和300—400 m的高丘陵，海岸线长度超过200 km，景观资源丰富。

3.1.2 研究数据 2012年以来深圳市政府直接出让的住宅用地中，90%以上为协议出让，多涉及城市更新等特殊政策，并非正常市场条件下的土地价格。经过抽样验证发现，一手房交易备案、二手房市场交易抽样数据基本能够反映所在时点的房地产价格水平，可作为研究数据基础。本文选用了2012—2014年的一手房价格数据及2010—2014年二手房价格数据作为基础数据，不包括保障性住房、城市更新等特殊情形。具体操作上，首先对数据进行验证处理，去除由于非正常交易等原因产生的异常样本点，其次借鉴土地估价中的剩余法，使用房地产楼面地价，扣除开发成本、税费、利息、开发商利润等项目，得到所在时点的地价水平，再根据土地剩余年期和地价指数开展年期修正和期日修正，最终得到以2015年1月1日为时点的楼面地价水平。剩余法估价过程中，充分考虑了不同密度等级、总层数、是否豪宅等因素对开发成本、利润等的影响。经过以上处理，得到住宅用地1021宗，空间上覆盖了深圳市主要建成区，全市建成区平均样本点密度为1.14个/km2，在原特区内的福田、罗湖、南山、盐田4区住宅地价样本密度较高，光明、大鹏两区地价样本密度最低，详见表1。住宅地价微观影响因素数据来源较多，主要是深圳市规划“一张图”、遥感影像提取、土地利用现状调查数据提取等，为保证数据准确性，对所提取的数据进行了抽样检查，对问题较多的数据，如综合性医院数据，进行了逐个调查修正。

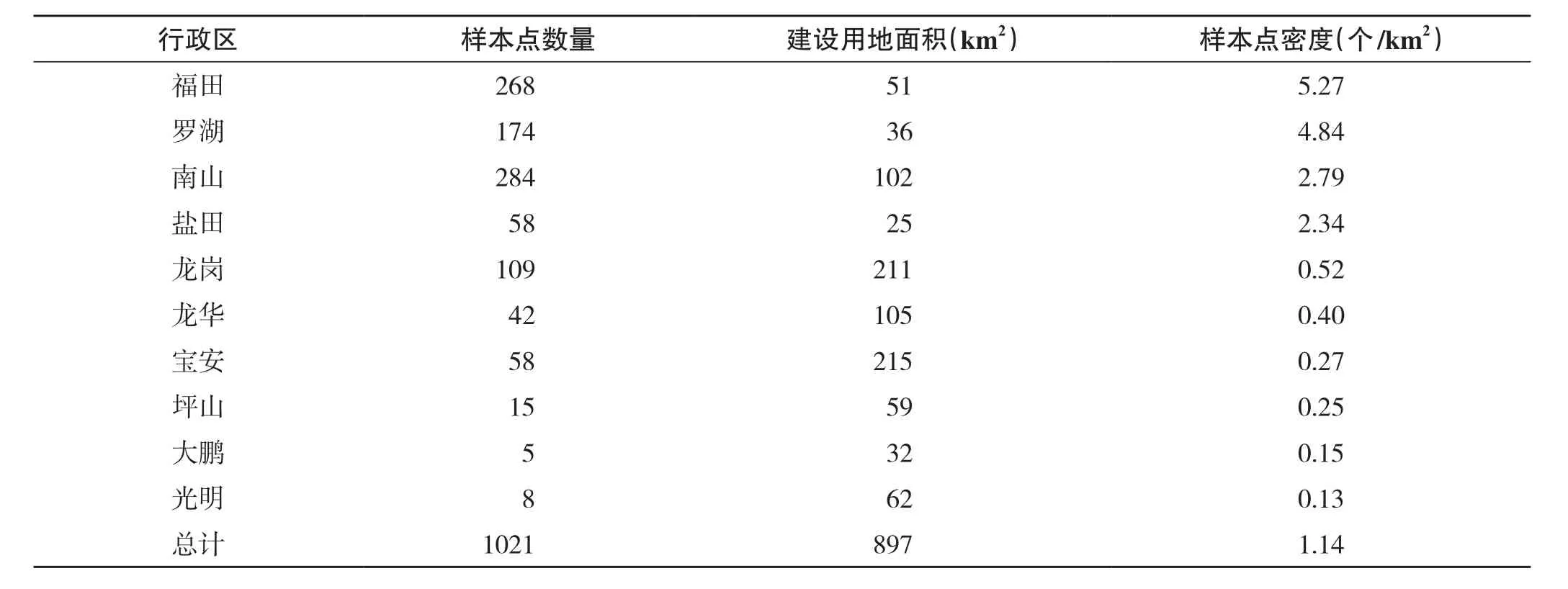
表1 地价样本点空间分布情况Tab.1 The spatial distribution of sample points about land price

3.2 GWR回归模型构建

3.2.1 回归因子选取 回归因子包括区域因素和个别因素两个方面。结合相关研究文献的结论与领域专家咨询结果可知，区域因素主要包括公共配套、区位条件、交通条件、城市规划、景观等[18-22]。对于住宅用地而言，最重要的公共配套资源为教育与医疗资源，可使用中小学校和医院反映；区位条件代表宗地与城市中心、副中心的关系，可使用商服中心反映；交通条件包括轨道交通、道路交通，但由于在其他因素量化时已经考虑道路交通因素，因此不需要将道路交通专门考虑，这里只单独考虑轨道交通；城市规划因素十分复杂，城市规划中的诸要素对地价的作用时段、作用范围受规划本身的知晓度以及公众理解影响较大，难以精确把握，故本文只选用普遍认为影响力最大的一项，即规划重点片区；景观因素中，城市景观对地价的影响与商服中心相关度高，且难以量化，研究选用对住宅地价影响较大的自然景观作为代表因素。个别因素方面，对地价作用较大的因素主要有容积率和地块面积两项[23-24]。

综上，本文最终确定了中小学校、医院、轨道交通、商服中心、规划重点片区、景观6方面的区域因素，结合容积率和地块面积两项个别因素作为回归因子。

3.2.2 GWR回归 从全市地价样本点中，随机选取80%的样本点用于模型构建，其余用于修正结果验证。为了判断使用GWR模型的必要性，首先对地价样本点进行空间自相关分析，结果表明，样本宗地楼面地价的Moran’s I指数为0.37，在0.01水平上显著，为显著正相关，具备使用GWR模型的条件。

使用样本点楼面地价作为回归因变量，将影响因素量化为容积率、地块面积、中学学位级别、小学学位级别、到市属国有综合医院时间、到区属国有综合医院时间、到现状轨道站点距离、到在建轨道站点距离、到市级商服中心时间、到区级商服中心时间、是否在规划重点片区内、到海岸线距离、到湖泊距离、到绿地距离14项指标作为自变量。首先构建全局回归模型，剔除显著性较差的到市属国有综合医院时间、到区属国有综合医院时间、到在建轨道站点距离、到区级商服中心、到绿地距离5项。使用剩余9项自变量用于GWR模型构建，带宽确定采用基于AICc的自适应方法，回归R2值为0.652，整体效果较好，自变量回归系数见表2。

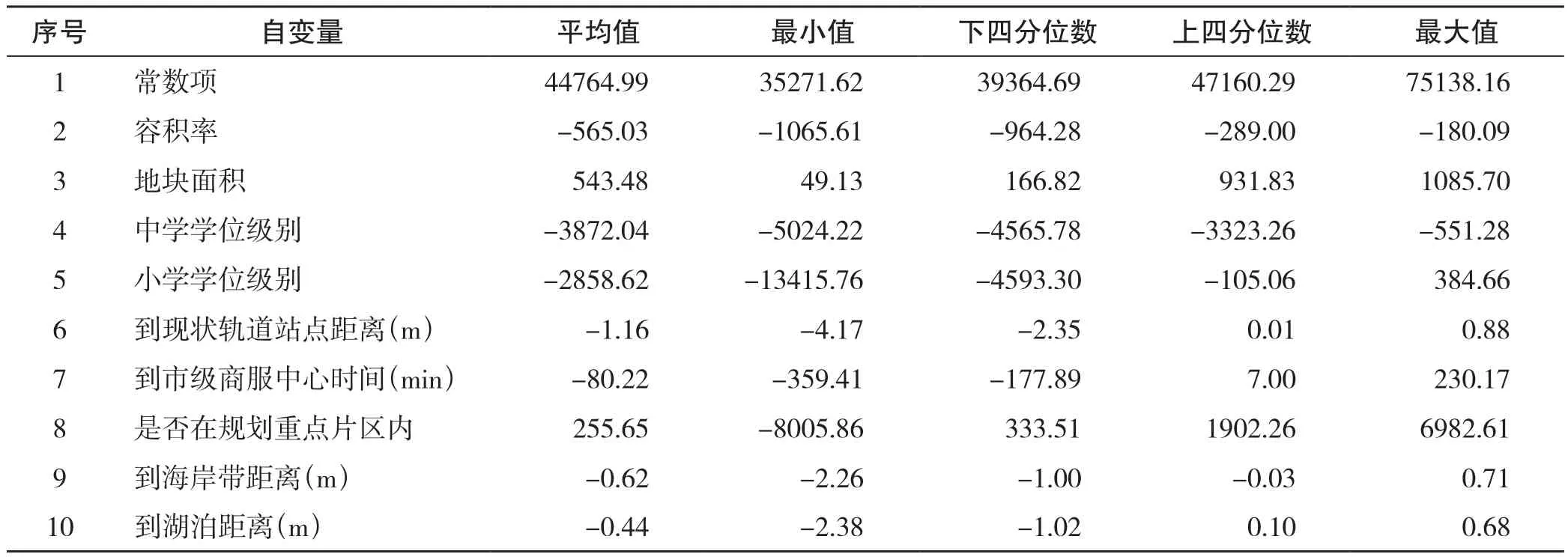
表2 住宅地价GWR模型回归系数Tab.2 The regression coefficients of GWR model for residential land price

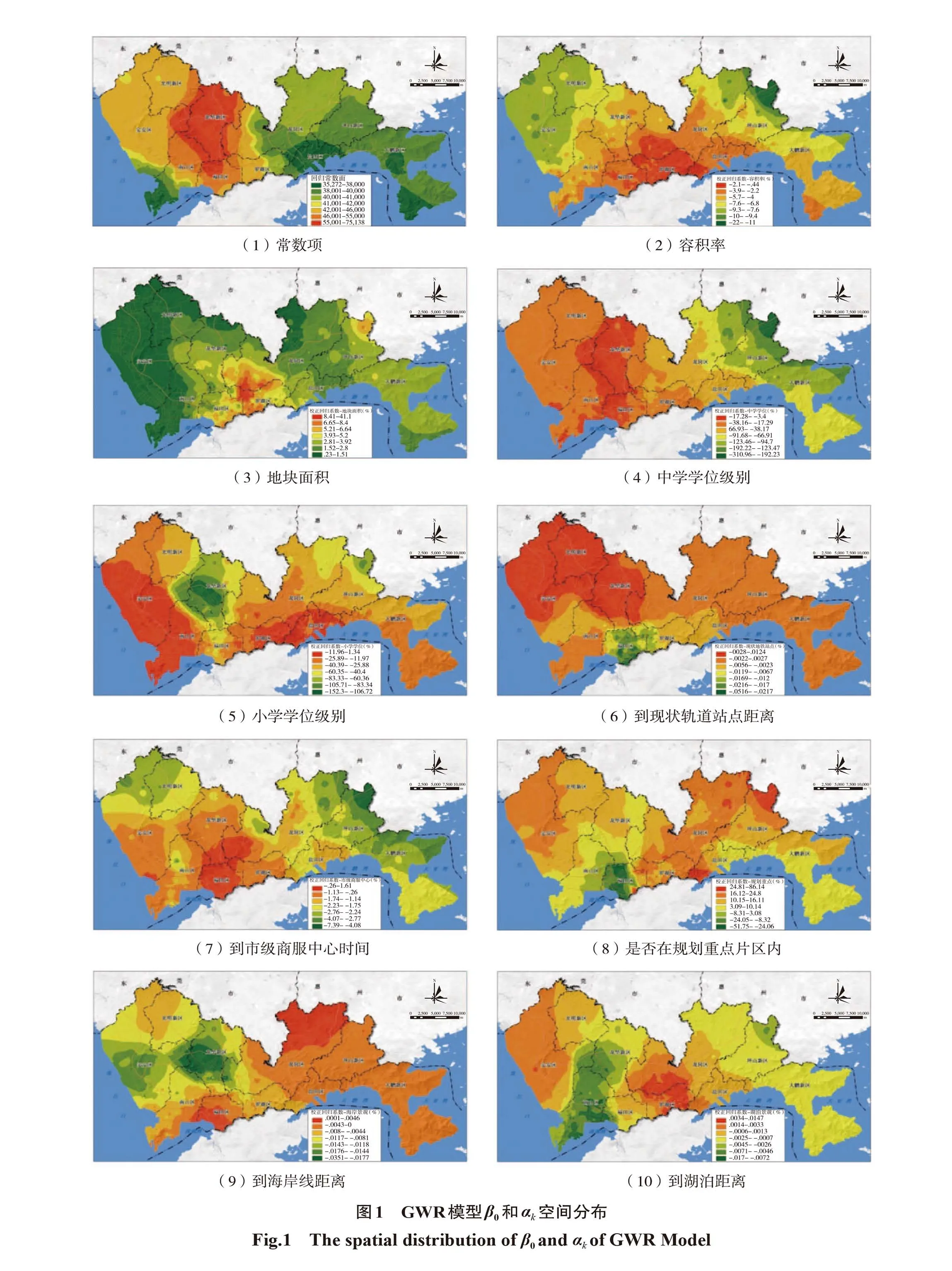
计算各回归样本点的校正回归系数αk（ui，vi），采用距离反转加权法空间内插得到β0和αk的空间栅格分布图（图1，封二）。可以看出，各影响因素对地价的作用在空间上均存在明显的空间非平稳性。

3.3 住宅地价修正分区生成

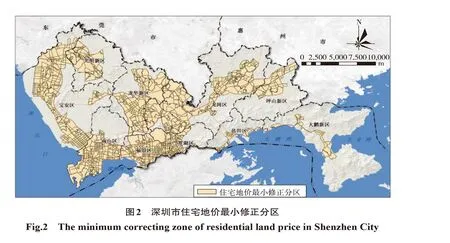
3.3.1 最小修正分区生成 住宅地价最小修正分区的设计以街区单元为基础，为保证运算效率和修正模型易用程度，使用高速公路、快速路、主干道、次干道4级道路作为街区划分依据。考虑规划重点片区、中小学学位等具有突变特征的影响因素边界可能与上述4级道路不相吻合，将规划重点片区、中学学位、小学学位3项影响因素的边界也加入到街区边界中，共同作为空间划分的依据。采用上述方法，得到住宅地价最小修正分区1579个，平均面积0.51 km2（图2，封三）。

3.3.2 修正分区合并 统计所有住宅地价最小修正分区中的回归常数项均值、各回归因子校正回归系数均值向量以及各回归因子校正回归系数标准差向量。对于最小修正分区i，上述三项统计量表示为Bi，A= （Ai1，Ai2，…，Ai9）T和S= （Si1，Si2，…，Si9）T。进一步计算最小修正分区内各校正回归系数的变异系数向量C= （Ci1，Ci2，…，Ci9）T，其中Cin=Sin/Ain（n= 1，2，…，9），用于衡量分区内校正回归系数的离散程度。

对于任意两个空间上相邻的住宅地价修正分区i和j，定义以下3项评价指标作为判断是否应当合并的依据：用以反映两个修正分区的各回归因子校正回归系数均值向量相似度，取值越小，相似度越强用以反映两个修正分区的回归常数项均值相似度，取值越小，相似度越强；k为假设i和j合并后的修正分区），用以反映两个修正分区合并后内部各回归因子的校正回归系数差异，该数值过大则表示两个分区不宜合并。

将所有住宅地价最小修正分区按照以下步骤操作：（1）计算所有住宅地价最小修正分区的回归常数项均值、各回归因子校正回归系数均值向量以及各回归因子校正回归系数标准差向量，对于相邻的修正分区，计算IA、IB和IC，得到相邻修正分区列表；（2）从相邻修正分区列表中筛选出所有满足IA＜0.15且IB＜0.15且IC＜0.5的修正分区组合；（3）从筛选出的修正分区组合中选取IA值最小的组合，合并该两个修正分区；（4）重新计算合并后修正分区的回归常数项均值、各回归因子校正回归系数均值向量以及各回归因子校正回归系数标准差向量，计算其与相邻单元的组合的IA、IB和IC，更新相邻修正分区列表；（5）重复步骤（2）、（3）、（4），直到无修正单元可供合并。

经过上述操作，得到住宅地价修正分区190个，平均面积4.24 km2（图3，封三）。

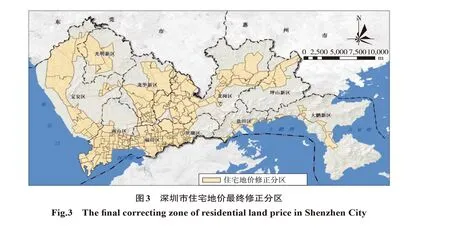
3.4 修正结果验证

住宅地价修正结果验证的方法为：对于地价验证点，使用修正公式将同一修正分区内的多个已知地价验证点价格修正为地价验证点价格，取平均值作为该验证点的修正地价。通过对比地价验证点的实际地价（Pa）和修正地价（Pc），计算绝对误差率（Er）：

参照《城镇土地估价规程》中对于市场比较法使用的规定“根据估价对象状况和估价目的，应从搜集的交易实例中选取3个以上的比较实例”，考虑样本点数限制，本验证规定同一修正分区内的比较实例不少于2个。通过筛选，满足该条件的地价验证点共72个。

经过使用所在修正分区内的地价点进行修正，得到地价验证点的楼面地价，72个地价验证点的修正地价绝对误差率最大39.64%，最小0.06%，平均值为14.61%，中位数12.84%。其中，69.4%的地价验证点绝对误差率分布在20%以内，绝对误差率大于30%的地价验证点较少，占9.7%。

绝对误差率空间分布见图4（封三），可以看出，原特区内福田、南山、罗湖的修正误差总体较低，原特区外的修正误差普遍偏高，其中福田区的总体误差水平最低。分析修正分区内回归样本点密度和绝对误差率的关系（图5），可见二者存在一定的负向关联，参与GWR模型的样本点密度每增加1个/km2，修正误差率下降0.91%，当样本点密度大于5时，修正的绝对误差率平均仅为11.06%。因此，在福田、南山等房地产市场活跃的地区，由于可获取的地价样本点数量较多，GWR模型能够更加细致地刻画影响因素对地价在每一位置的影响，而在原特区外的宝安、光明、龙岗、坪山等区地价点数量较少的地区，GWR模型不能精确地反映影响因素对地价作用的空间分异特征，因此采用该方法修正偏差相对较大。

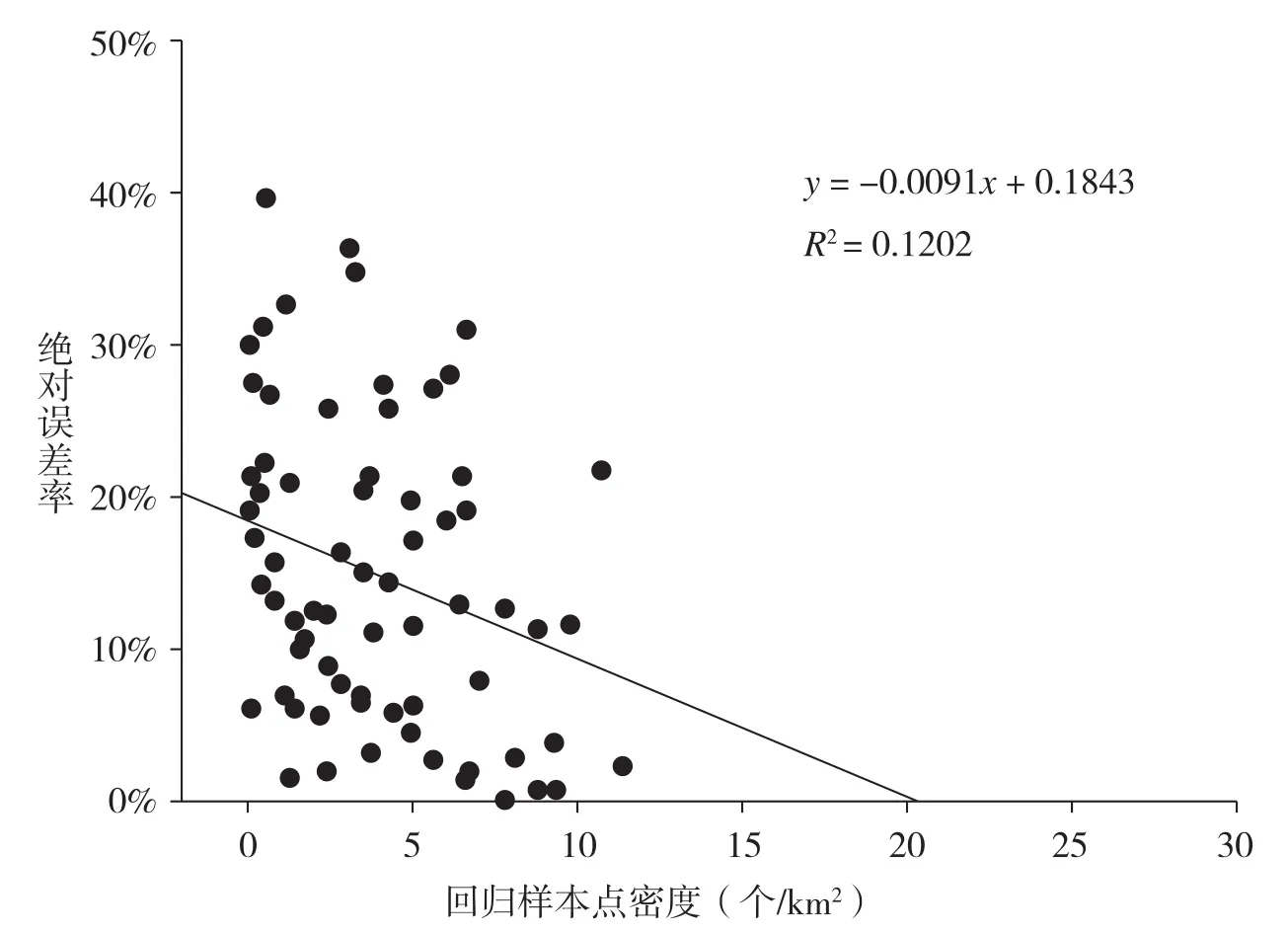
图5 回归样本点密度与绝对误差率的关系Fig.5 The relationship between sample point density and absolute error rate

3.5 方法实用性分析

从估价目的来看，本文提出的地价相对修正方法以正常市场条件下的土地价格样本作为回归模型的构建基础，旨在得到正常市场条件下的土地价格，能够客观掌握土地的实际市场价值，可直接用于新增土地供应中的土地拍卖底价和挂牌价格确定。就深圳市而言，虽然目前土地以存量供应为主，近年来出让的住宅土地多涉及城市更新等特殊政策，但这些政策制定过程中所涉及的利益分配测算等问题必须考虑土地在正常市场条件下的价值。此外，掌握正常市场条件下的土地价格也是与土地有关各类经济活动的关键，例如地价监测与指数发布、标定地价评估、补交地价、土地抵押等。从估价结果精度来看，修正结果绝对误差率平均值为14.61%，特别在样本点密集地区，修正误差可控制在更低的水平，能够为地价评估提供一定参考。

4 结论

本文针对市场比较法在使用过程中面临的关键问题，引入GWR模型刻画住宅地价影响因素与住宅地价的空间分异，提出了一种自下而上的修正分区生成流程，构建了一种住宅地价相对修正方法，主要结论如下：

（1）本文构建的住宅地价相对修正模型具有实操可行性。本文通过选取9项因子构建覆盖全深圳市的住宅地价GWR模型，并以此为基础构建住宅地价相对修正模型。验证结果表明，全市范围内绝对误差率平均值为14.61%，约70%的验证点修正误差在20%以内。此外，该方法与《城镇土地估价规程》中的市场比较法相兼容，具有一定的实际应用价值。

（2）地价修正精度与GWR模型构建精度正相关。通过分析可知，在GWR模型样本点密度较高的地区，地价修正精度较高，在样本点密度较低的地区，地价修正精度也相应较低。平均来看，参与GWR模型的样本点密度每增加1个/km2，修正误差率下降0.91%，当样本点密度大于5时，修正的绝对误差率平均仅为11.06%。增加有效样本点密度，提高GWR模型的构建精度是提升地价修正精度的关键。

（3）该方法更加适用于地产市场活跃地区。与常规市场比较法类似地，该方法适用于地产市场活跃地区，原因如下：①在数据收集处理环节，发达的地产市场能够提供时间较近、数量较大的地价样本点，有助于自动识别并剔除原始数据中的各类异常值，保证回归分析的准确性；②在GWR模型构建环节，发达的地产市场能够提供足够密集的地价样本点，保证GWR模型构建的空间精度；③在地价修正环节，发达的地产市场能够在一个修正分区内提供足够数量的比较实例，保证修正结果的可信度。

（References）：

［1］ GB/T 18508-2014. 城镇土地估价规程［S］ . 2014.

［2］ 王秀丽，李恒凯，刘小生. 基于GIS的房地产市场比较法评估模型研究［J］ . 中国土地科学, 2011，2（510）：70 - 76.

［3］ 李恒凯，郝雷，刘德儿. GIS改进市场比较法估价的研究与实践［J］ . 测绘科学, 2011（，1）：204 - 206.

［4］ Court A. T. Hedonic price indexes with automotive examples［J］ . The Dynamics of Automobile Demand，1939.

［5］ Bender Bruce, Hwang Hae-Shin. Hedonic housing price indices and secondary employment centers［J］ . Journal of Urban Economics,1985，1（71）：90 - 107.

［6］ Shonkwiler J. S., Reynolds J. E. A Note on the Use of Hedonic Price Models in the Analysis of Land Prices at the Urban Fringe［J］ .Land Economics，1986，6（21）：58 - 63.

［7］ Tokuda Masaaki. Consideration of Relation between Characteristic and Price of Land by Hedonic Approach: The Residential Quarter in Shiga Prefecture as a Case Study［J］ . 2009.

［8］ Lancaster K. J. A New Approach to Consumer Theory［J］ . The Journal of Political Economy，1966：132 - 157.

［9］ 周林林. 基于特征价格模型的城市住宅用地价格影响因素研究［D］ . 上海：华东师范大学，2015：76.

［10］ Straszhein M. Hedonic Estimation of Housing Market Pirce: A Further Commen［tJ］ . Review of Economic and Statistics，1974，5（63）：404 - 406.

［11］ Goodman A. C. Hedonic Prices, Price Indices and Housing Markets［J］ . Journal of Urban Economics，1978，（54）：471 - 484.

［12］ Capozza D., Helsley R. W. The Fundamentals of Land Prices and Urban Growth［J］ . Journal of Urban Economics，1989，2（63）：295 -306.

［13］ Michaels R. G., Smith V. K. Market Segmentation and Valuing Amenities with Hedonic Model: The Case of Hazardous Waste Site［J］ .Journal of Urban Economics，1990，28（2）：223 - 242.

［14］ Hu Shougeng, Yang Shengfu, Li Weidong, et al. Spatially non-stationary relationships between urban residential land price and impact factors in Wuhan city, China［J］ . Applied Geography，2016，68（68）：48 - 56.

［15］ Brunsdon Chris, Fotheringham A. Stewart, Charlton Martin. Some Notes on Parametric Significance Tests for Geographically Weighted Regression［J］ . Journal of Regional Science，1999，39（3）：497 - 524.

［16］ 李志，周生路，张红富，等. 基于GWR模型的南京市住宅地价影响因素及其边际价格作用研究［J］ . 中国土地科学，2009，23（10）：20 - 25.

［17］ Fotheringham A. S., Brunsdon C., Charlton M. Geographically Weighted Regressing: The Analysis of Spatially Varying Relationships［M］ . Hoboken: Wiley，2003.

［18］ 任辉，吴群. 基于ESDA的城市住宅地价时空分异研究——以南京市为例［J］ . 经济地理，2011，31（5）：760 - 765.

［19］ Mcdonald John F., Osuji Clifford I. The effect of anticipated transportation improvement on residential land values［J］ . Regional Science amp; Urban Economics，1995，25（3）：261 - 278.

［20］ Villalobos Emmanuel. Housing attribute preferences in El Paso［J］ . Dissertations amp; Theses-Gradworks，2010.

［21］ Jahanshahloo L., Salahshour S. Fuzzy effects of urban landscapes on land prices［J］ . Procedia Computer Science，2011，3：595 - 599.

［22］ 董冠鹏，张文忠，武文杰，等. 北京城市住宅土地市场空间异质性模拟与预测［J］ . 地理学报，2011，66（6）：750 - 760.

［23］ 欧阳安蛟. 容积率影响地价的规律及修正系数确定法［J］ . 经济地理，1996，（1）：97 - 101.

［24］ 罗罡辉，吴次芳，郑娟尔. 宗地面积对住宅地价的影响［J］ . 中国土地科学，2007，21（5）：66 - 69.

Study on the Correcting Method of Residential Land Price based on GWR: A Case Study of Shenzhen City

HU Wei1，2, LIU Yong-xue2，3, LIN Yong-jun1，2
（1. Shenzhen Urban Planning amp; Land Resource Research Center, Shenzhen 518040, China; 2. Key Laboratory of Urban Land Resources Monitoring and Simulation, Ministry of Land and Resources, Shenzhen 518034, China; 3. School of Geographic and Oceanographic Sciences, Nanjing University, Nanjing 210023, China）

The purpose of the study is to propose a correcting method of residential land price, which is suitable for the regions with active estate market, to solve the problem of traditional market comparison approach that relies too much on experience of the appraisers. The research methods are as follows. The GWR model is introduced to measure the spatial differentiated law of the impact factors of residential land price, and to determine the correcting percentage in light of each unit change of impact factors. A spatial unit similarity evaluation method is developed to generate the residential land price correcting zone from bottom to top. The research results show that starting from the principle of GWR model,the correcting formula based on objective data is established and a complete technical route containing the regression model building, correcting zone generating and land price correcting is developed. The proposed method achieves good effect in the test by using real data. In conclusion, the proposed method has feasibility in the actual land appraisal work;the precision of land price correcting is positively associated with the precision of GWR model; and this method is more suitable for the regions with active estate market which have high density of land price sample points.

land economy; residential land price; land price correcting; GWR; Shenzhen City

F301.3

A

1001-8158（2017）09-0062-08

10.11994/zgtdkx.20171027.122254

2017-02-04；

2017-05-24

国土资源部城市土地资源监测与仿真重点实验室开放基金（KF-2015-01-036）。

胡炜（1988-），男，河南信阳人，硕士。主要研究方向为GIS应用与土地管理。E-mail: have211@163.com

刘永学（1976-），男，江苏扬州人，教授，博士生导师。主要研究方向为地图学与GIS。E-mail: yongxue@nju.edu.cn

（本文责编：陈美景）