基于流固耦合的减振器复原阀外特性分析

叶万权，杨礼康，杜嘉鑫，周安江

(浙江科技学院 机械与汽车工程学院，杭州 310023)

基于流固耦合的减振器复原阀外特性分析

叶万权，杨礼康，杜嘉鑫，周安江

(浙江科技学院 机械与汽车工程学院，杭州 310023)

为了研究液压减振器弹性复原阀对阻尼力的影响，使用ADINA有限元软件，并结合流固耦合相关理论，构建了固体有限元模型及减振油流体有限元模型。通过相关软件后处理进行计算与求解，获得了该减振器的示功特性和速度特性。在此基础上，对该型号液压减振器进行试验验证，并将前后结果进行对比，结果表明所建立的有限元网格模型准确有效。

流固耦合；液压减振器；复原阀；示功特性

减振器是车辆底盘减振系统不可或缺的部分，汽车的整体舒适性和稳定性都与其工作性能息息相关[1]。其中，内部活塞和与活塞配合使用的弹性阀片是液压减振器产生阻尼力的主要元件[2-4]。因此，在研究减振器性能状况时，首先要对这些主要零部件进行分析。如今较为常见的方法是利用半经验公式及实际试验数据对车辆减振器进行开发[5]，但这样做不仅导致开发周期较长，而且不易获得减振器弹性阀片开度对阻尼力影响程度的性能参数。对此，笔者结合流固耦合(fluid-structure interaction, FSI)相关理论[6-8]，利用动态增量非线性分析(ADINA)软件建立了车辆液压减振器复原阀系有限元网格模型，从而得到了减振器示功图和阻尼力-速度曲线，再利用减振器测试系统进行试验，将仿真与试验结果进行对比分析。

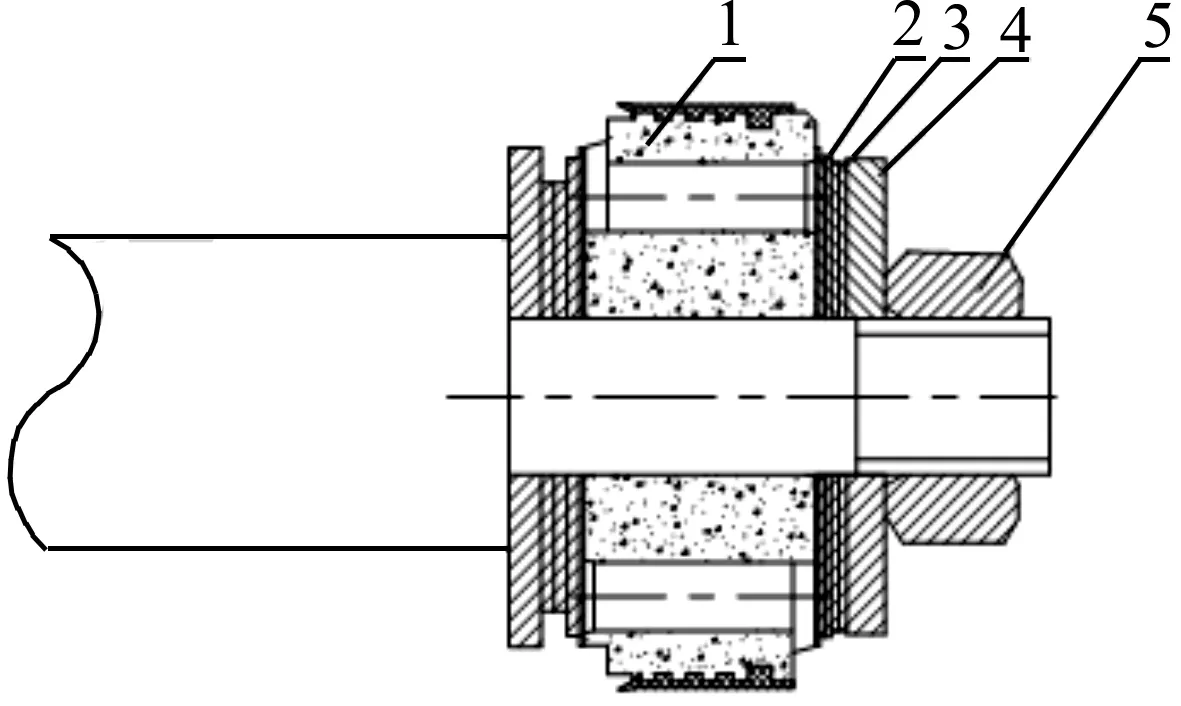
1—活塞；2—节流阀片；3—调整片； 4—限位片；5—自锁螺母。图1 液压减振器复原阀系Fig.1 Restoring valve system of hydraulic shock absorber

1 减振器弹性阀系结构原理分析

液压减振器复原阀总成剖视图见图1。对液压减振器复原阀系而言，当活塞杆所受复原拉力较小时，内筒压力差同样较小，液压油经活塞常通孔和节流阀片缝隙从工作缸上腔室流入工作缸下腔室，此时复原弹性阀片等没有发生变形，减振器复原阀就未开阀，减振器阻尼力主要由节流阀片缝隙所产生[9]；当活塞杆所受复原拉力较大时，内筒的压力差将增大，此时弹性阀片将产生形变，阀系开阀，减振器阻尼力将受弹性复原阀片的变形量影响[10]。

2 建立减振器FSI模型

2.1 FSI基本分析理论

FSI分析方法是研究流体和固体相互作用的常用方法，它可以分析并解决两者物态之间因受力而相互作用所导致的固体形变、流体运动等相关技术问题。其研究分析理论需要运用流体耦合动力学方程、固体耦合动力学及两种物态相应的相关运动学方程。

设定n为单位外法线矢量，流体、固体两者对应需要满足的条件方程[11]分别为:

nτf=nτs，

(1)

df=ds。

(2)

式(1)～(2)中:τf为流体应力；τs为固体应力；df与ds为对应物态的边界位移量。

由式(1)可推导出流体速度vf与固体速度vs的关系式：

nvf=nvs。

(3)

2.2 基于ADINA的模型建立

固体模型和液体模型单独构建。在ADINA中划分模型的网格时，由于该软件针对FSI面上不同精度的有限元网格具有自适应计算的能力，为了保证求解结果相对准确且尽量减少耦合计算所消耗的大量时间，减振器阀系各部件的网格密度并没有必要保持一致，即保证网格达到一定的容差即可；对计算结果有较大影响的阀片采用较细化的网格，而对计算结果影响较小的部件(例如活塞杆)则采用较大密度的网格，网格划分的节点数及单元数分别为：液体模型81 372个节点及390 279个单元，固体模型61 256个节点及27 1457个单元。经有限元模拟计算后发现，在仿真过程中，液体模型按时间步流动变化，而固体的动网格部分会随着流体压力的变大而发生形变；随着时间步的结束，弹性阀系也会自动恢复为初始状态，相比于仿真前，模型并没有发生明显变化。

针对两物态有限元模型，要认真思考并合理去掉那些虽然不影响计算结果精度，但影响计算速率的相关零部件。例如，可以将液压减振器的内筒视为不可形变的刚体进行分析系统简化[12-14]。液压减振器复原阀系的流、固网格模型如图2～3所示。

针对有限元模型网格划分单元的选取，在充分考虑FSI面上的密度相容性问题的基础上，均一致使用小六面体(8节点)结构单元。关于流固耦合面，为了减少所建模型的复杂程度及求解时间，在所建模型中仅将与活塞运动方向相同且与耦合正面相互作用的阀片定义为耦合面，其他均定义为非滑移面。

图2 流场有限元网格模型Fig.2 Finite element mesh model of flow field

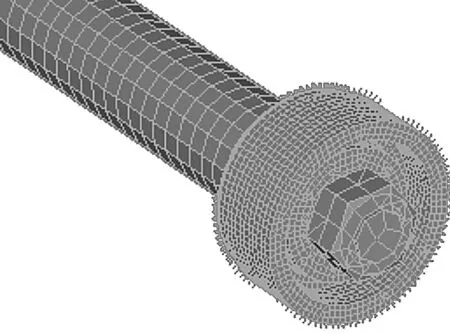
图3 固体有限元网格模型Fig.3 Solid finite element mesh model

3 模型计算及试验分析

3.1 模型后处理

为了有效提高计算的收敛性，两个有限元模型的对应面空间位置应该尽量相同，这样做不但保证了计算的精度，而且可以消除一些不确定因素所造成的影响[15]。固体模型包含复原阀片、复原调整阀片、节流片等6个阀片。其中，减振器复原阀片单片厚度为0.15 mm，直径为20.5 mm；复原调整阀片单片厚度为0.4 mm，直径为15.5 mm；复原节流片单片厚度为2.0 mm，直径为20 mm。结合相关理论，本研究利用隐式动态分析法对固体有限元网格模型进行求解。同时，根据实际流场流动的情况，将其网格模型设成从零开始的正弦波，并在出口处位置不设定流场边界条件。其中，由于液压油密度变化非常小，所以将其设定为不可压缩液体，并采用瞬态流动理论计算。另外，减振器的工作缸已经规定为刚性材料，因此内缸壁在软件中设置为wall。在液压减振器耦合部分计算时，本研究将两物态有限元网格模型放于一个整体矩阵中，设定λd、λτ分别为位移松弛因子和应力松弛因子，具体式子如下:

(4)

Xk+1=Xk+ΔXk，

(5)

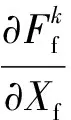
(6)

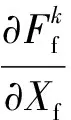
(7)

图4 MTS849型阻尼力测试系统Fig.4 MTS849 damping force test system

对于减振器固体网格模型，虽然采用六面体单元能够使计算结果更加精确，但求解所需的时间将大大延长。因此，不仅要通过经验和实际操作设置合适的求解收敛因子(此处根据实际计算测试选定收敛因子为0.8，对应的计算结果收敛最快)，而且要忽略除节流片位置外的其余部件动网格。此外，在设定时间步长时，要在求解效率和计算收敛性之间保持平衡。其中，在耦合计算的过程中，可以利用流体四周的固体节点位移经过数值插值计算求出油液流动节点的位移量，以及利用固体周围流体的应力积分计算求出固体节点的位移量。

3.2 试验分析

实际验证试验在某企业MTS849型减振器测试系统上进行，如图4所示。

测试过程中，运动行程设定为±25 mm，设定常规速度测试点，分别为0.052、0.131、0.262、0.393 m/s，测得各点的阻尼力并绘制示功图。设置试验系统的测试频率值，获得对应的速度特性曲线。为了减少测试误差，取多组试验的均值作为最终测试结果，最后将仿真与试验结果进行对比，如图5～6所示。

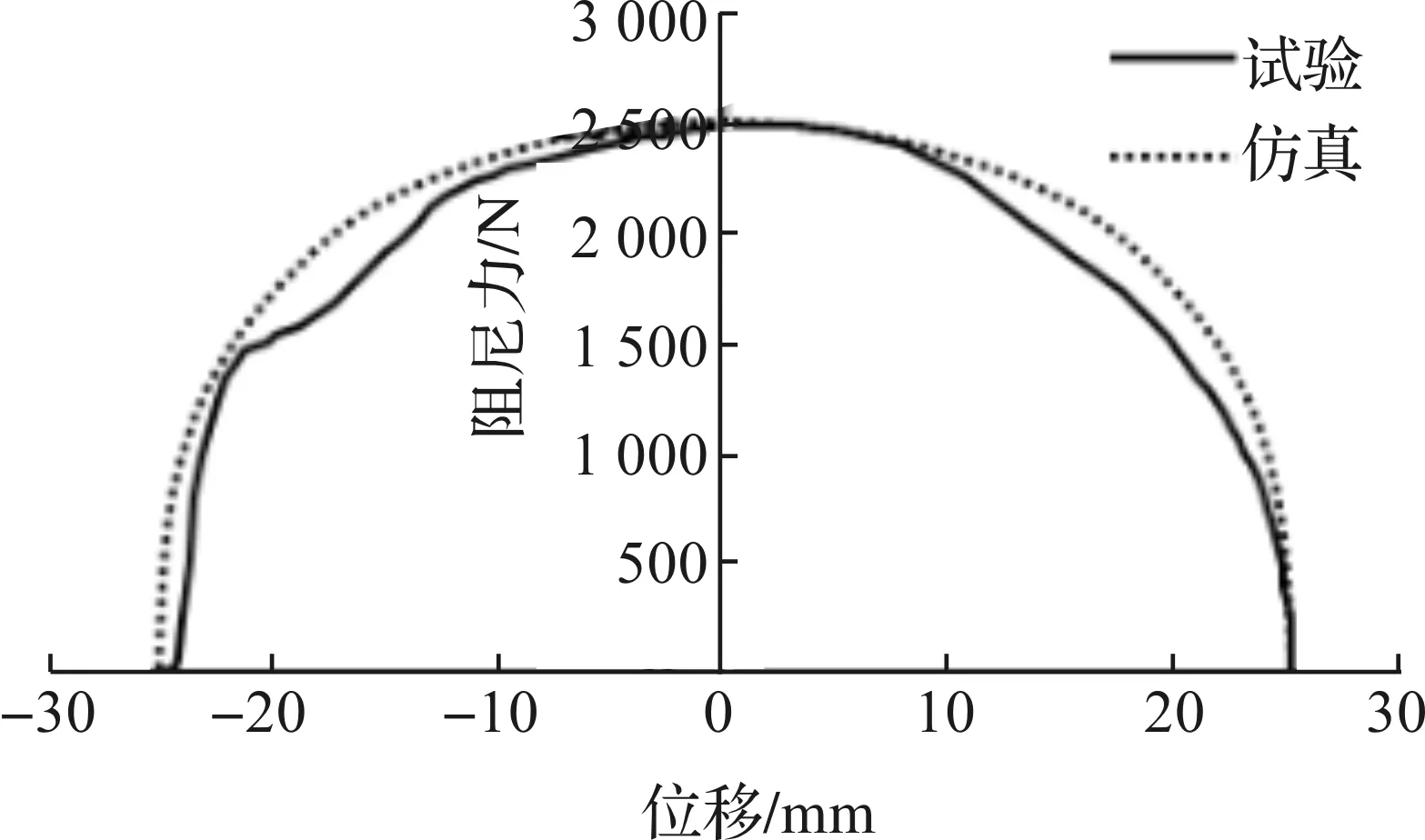
图5 仿真与试验的示功图对比Fig.5 Comparison of indicated work between simulation and test

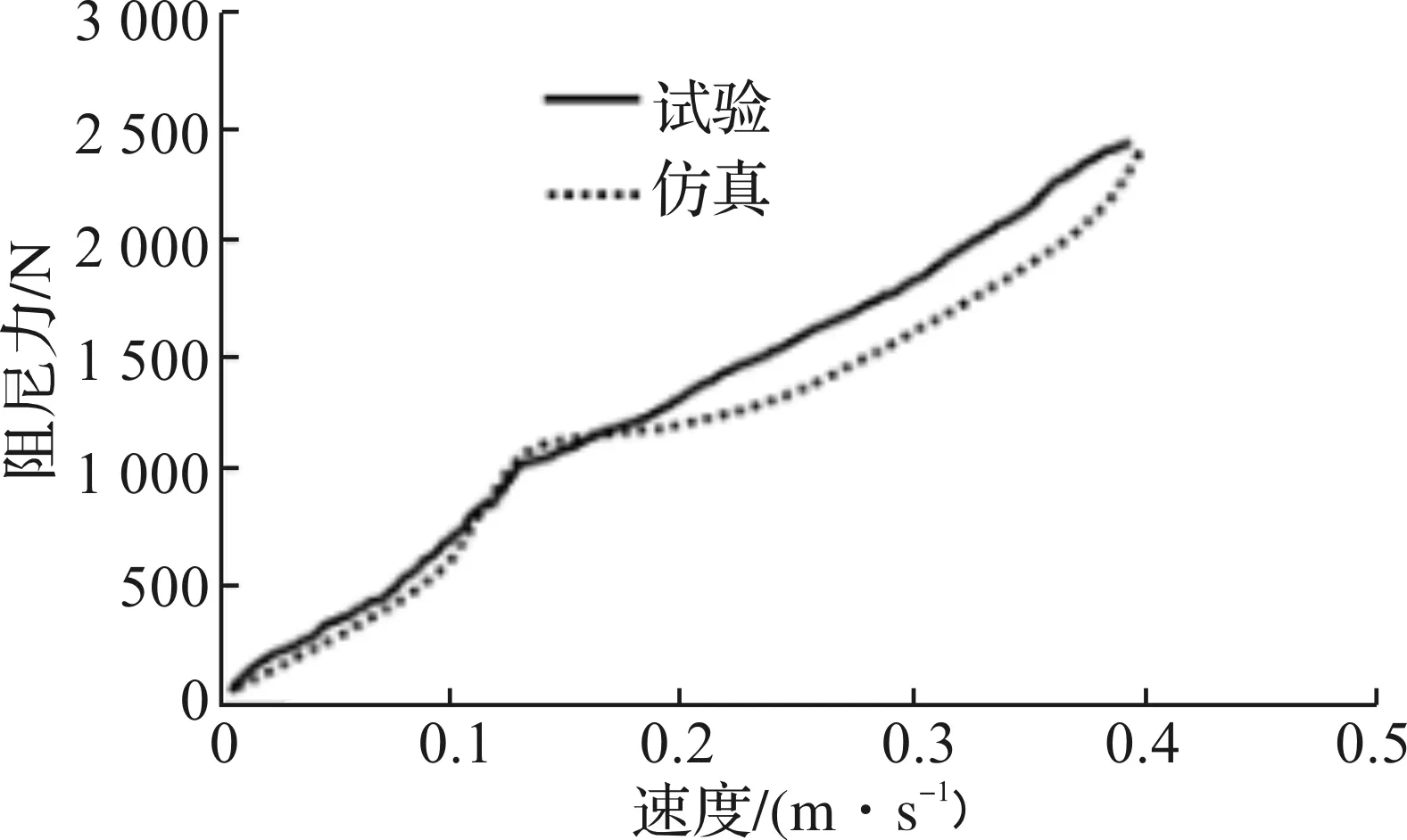
图6 仿真与试验的速度特性图对比Fig.6 Comparison of speed characteristics between simulation and test

经计算发现，双筒液压减振器仿真与试验结果之间误差范围均小于15%，符合要求的误差范围；而且速度曲线分段特征显著，符合理论依据及实际的液压减振器工作过程。

在ADINA软件计算分析中发现，在0.08、0.42 s两时间点时，复原阀系呈现两种状态，即分别为复原阀开阀前及其开阀后。从开阀前、后液体节流通道压力场可以看出：在活塞低速时，内部压力均匀分布，减振油为层流流动，此时弹性阀片没有开启；随着速度的增加，阀片开阀，减振油变为湍流流动。

4 结 论

本研究应用ADINA有限元分析软件构建某型汽车液压减振器复原弹性阀系，以及油液的有限元分析模型，并通过对有限元模型进行流固耦合分析及软件后处理计算获得仿真结果。减振器实际试验测试结果与计算仿真结果的对比表明，两者结果较为一致，从而证明此种分析方法能够有效解决和预测液压减振器的阻尼特性问题。但是，由于仿真设备的限制等，模型网格的划分并未达到足够的精细程度，仿真与实验结果误差仍然存在，尤其在高速段。因此，该模型仍有待进一步优化。

[1] LEE C T，MOON B Y．Simulation and experimental validation of vehicle dynamic characteristics for displacement sensitive shock absorber using fluid-flow modeling [J]．Mechanical Systems and Signal Processing，2006，20(2)：373．

[2] 戎红俊，彭宇明，李国华，等．基于AMESim的汽车液压减振器失效仿真[J]．液压与气动，2016(5)：26．

[3] 杨明亮，李人宪，丁渭平，等．阀系参数对高速列车液压减振器阻尼特性的影响[J]．西南交通大学学报，2014，49(2)：291．

[4] 马天飞，崔泽飞，佟静．基于Isight和AMESim的液压减振器关键参数集成优化[J]．汽车工程，2015,37(1)：97．

[5] 于振环，刘顺安，张娜，等．磁流变减振器多场耦合仿真分析[J]．农业机械学报，2014,45(1)：1．

[6] 贺李平，顾亮，龙凯，等．基于流-固耦合的汽车减振器动态特性仿真分析[J]．机械工程学报，2012,48(13)：96．

[7] 吴英龙，王萌，赵华，等．筒式减振器瞬态双向流固耦合仿真系统的开发设计[J]．机械科学与技术，2013,32(12)：1722．

[8] 李万林．基于流-固耦合的汽车减振器仿真研究[D]．长春：吉林大学，2014．

[9] 张佳明，王文瑞，詹思源．叶片式液压减振器流场特性仿真研究[J]．液压与气动，2016(6)：8．

[10] 袁光明，周长城．液压减振器节流损失及对阀系参数设计影响[J]．液压与气动，2008(8)：1．

[11] 于振环，张娜，刘顺安．基于流-固耦合的车辆减振器动态非线性仿真分析[J]．吉林大学学报(工学版)，2015,45(1)：16．

[12] 汪明明．液力减振器结构异响形成过程的流固耦合仿真与分析[D]．重庆：重庆大学，2014．

[13] 李小波，沈季胜，宁晓斌，等．基于流固耦合分析方法的减振器复原阀节流特性研究[J]．机械制造与自动化，2010,39(4)：20．

[14] 何联格．液力减振器流固耦合仿真与结构异响分析[D]．重庆：重庆大学，2011．

[15] 岳戈，梁宇白，陈晨，等．ADINA流体与流固耦合功能的高级应用[M]．北京：人民交通出版社，2010．

Analysisonexternalcharacteristicsoftherestoringvalveofshockabsorberbasedonfluid-structureinteraction

YE Wanquan, YANG Likang, DU Jiaxin, ZHOU Anjiang

(School of Mechanical and Automotive Engineering, Zhejiang University of Science and Technology, Hangzhou 310023, Zhejiang, China)

In order to study the effect of the elastic restoring valve of hydraulic shock absorber on the damping force, this study employed the ADINA software, in combination with the fluid-structure interaction theory, to construct the solid finite element model and the fluid finite element model of damping oil. Through relevant software post-processing calculation, this study obtained the indicated work and speed characteristics of the shock absorber. On this basis, the hydraulic shock absorber has been tested and verified. By comparing the results before and after the test, the results show that the established finite element mesh model is accurate and effective.

fluid structure interaction(FSI); hydraulic shock absorber; restoring valve; indicated work characteristics

TH703.63

A

1671-8798(2017)06-0429-04

10.3969/j.issn.1671-8798.2017.06.006

2017-08-21

国家自然科学基金项目(51175474)；浙江省大学生创新创业孵化项目(2016R415004)；浙江科技学院研究生科研创新基金项目(2016yjskc005)

杨礼康(1971— )，男，山西省闻喜人，教授，博士，主要从事磁流变减振器研究。E-mail:104019@zust.edu.cn。