浅谈同种气体变质量问题的解法

河北 杨高轩

(作者单位：河北省石家庄市河北正定中学)

在多变的物理问题中追寻某些不变性是极为重要的研究方向。

浅谈同种气体变质量问题的解法

人教版选修3—3在讲授三个理想气体实验定律的基础上得出了理想气体状态方程，值得注意的是它们的适用条件为一定质量的理想气体，对于气体变质量问题显得有些捉襟见肘，于是“等效法”“气缸模型法”“气片模型法”“气体分态式法”等应运而生，这些方法抽象难懂，对学生解决问题未必是好方法，我从实际教学的角度浅谈同种气体变质量问题的求解方法。

一、气体密度方程

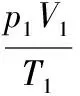
【例1】空气压缩机的储气罐中储有1.0 atm的空气6.0 L，现再充入1.0 atm的空气9.0 L。设充气过程为等温过程，空气可看做理想气体，则充气后储气罐中气体压强为

( )

A．2.5 atm B．2.0 atm

C．1.5 atm D．1.0 atm

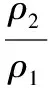
【答案】A

【例2】容积为20 L的钢瓶充满氧气后，压强为150 atm，打开钢瓶的阀门让氧气同时分装到容积为5 L的小瓶中，若小瓶原来是抽空的，小瓶中充气后压强为10 atm，分装过程中无漏气，且温度不变，那么最多能分装

( )

A．4瓶 B．50瓶

C．56瓶 D．60瓶

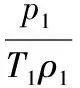
【答案】C

【例3】如图1所示，有一截面积为S=100 cm2的导热气缸，气缸内部有一固定支架AB，支架上方有一放气孔，支架到气缸底部距离为h=2 cm，活塞置于支架上，开始时气缸内部封闭气体的温度为300 K，压强为大气压强p0=105Pa。当外界温度缓慢上升至303 K时，活塞恰好被整体顶起，气体由放气孔放出少许，活塞又回到支架处，气缸内气体压强减为p0，气体温度保持303 K不变。整个过程中封闭气体均视为理想气体，已知外界大气压强恒为p0，重力加速度为g，不计活塞与气缸的摩擦，求：

(1)活塞的质量；

(2)活塞被顶起过程中放出的气体的体积。

【解析】(1)放气前气体密度不变，根据

根据平衡条件可得

mg+p0S=p1S

解得：m=1 kg。

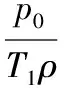
放气后气体的体积与原来的体积满足

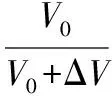
又V0=Sh

解得：ΔV=2×10-6m3。

二、质量守恒思想

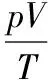
【例4】如图2所示为一太阳能空气集热器，底面及侧面为隔热材料，顶面为透明玻璃板，集热器容积为V0，开始时内部封闭气体的压强为p0。经过太阳曝晒，气体温度由T0=300 K升至T1=400 K。缓慢抽出部分气体，并使温度降为360 K，此时，集热器内气体的压强回到p0，求集热器内剩余气体的质量与原来总质量的比值。

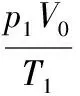
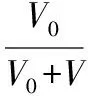
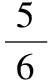
【例5】如图3所示，一底面积为S、内壁光滑的圆柱形容器竖直放置在水平地面上，开口向上，内有两个质量均为m的相同活塞A和B；在A与B之间、B与容器底面之间分别封有一定量的同样的理想气体，平衡时体积均为V。已知容器内气体温度始终不变，重力加速度大小为g，外界大气压强为p0，现假设活塞B发生缓慢漏气，致使B最终与容器底面接触。求活塞A移动的距离。

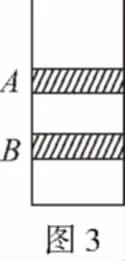
【解析】设A与B之间、B与容器底部之间的气体压强分别为p1、p2，漏气前

B最终与容器底面接触后，AB间的压强为p，气体体积为V3，则有

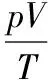
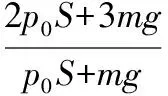
故活塞A移动的距离为

(作者单位：河北省石家庄市河北正定中学)