论新课标高考中的抛体运动命题及应对策略

江苏 邱爱东

(作者单位：浙江省东阳市第二高级中学)

(作者单位：江苏省江阴市江阴初级中学)

探讨命题特点，寻觅高考“踪迹”。

论新课标高考中的抛体运动命题及应对策略

曲线运动是新课标高考命题的热点和重点，而平抛运动作为两大典型的曲线运动之一，在高考命题中连续不断，命题难度中等，但是命题的形式有变化，所以本文就此探讨，希望读者在复习中进一步活用基础知识解决更多的变化问题。

一、多体平抛运动的分析与比较

【例1】(2017·全国卷Ⅰ)发球机从同一高度向正前方依次水平射出两个速度不同的乒乓球(忽略空气的影响)。速度较大的球越过球网，速度较小的球没有越过球网，其原因是

( )

A．速度较小的球下降相同距离所用的时间较多

B．速度较小的球在下降相同距离时在竖直方向上的速度较大

C．速度较大的球通过同一水平距离所用的时间较少

D．速度较大的球在相同时间间隔内下降的距离较大

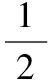
B．斜面体受桌面的支持力为(m+M)g

C．斜面体受桌面的摩擦力为mgcosθ

D．斜面体受桌面的摩擦力为mgsinθcosθ

【解析】此题采用解法一将会耗费学生大量时间，且增加出错概率。所以，我们采用解法二，利用加速度去求解桌面对斜面体的支持力和摩擦力。

对小木块和斜面体组成的系统进行分析，系统中的一部分(小木块)存在沿斜面向下的加速度。这个加速度可以分解为两种效果：水平方向和竖直方向的分加速度。

小木块加速度：gsinθ沿斜面向下

水平方向加速度为：gsinθcosθ水平向左

竖直方向加速度为：gsinθsinθ竖直向下

对于系统而言，应该存在水平向左的合外力和竖直向下的合外力。

水平向左的合外力只能由桌面给的摩擦力提供，故桌面给斜面体的摩擦力为：Ff=mgsinθcosθ；竖直向下的合外力由桌面的支持力和系统的重力提供：(M+m)g-FN=mgsin2θ，FN=Mg+mgcos2θ，故本题选D。

【变式】(2012·南昌一模)如图，质量为M的三角形木块A静止在水平面上。一质量为m的物体B正沿A的斜面下滑，三角形木块A仍然保持静止。则下列说法中正确的是

( )

A．A对地面的压力可能小于(M+m)g

B．水平面对A的静摩擦力可能水平向左

C．水平面对A的静摩擦力不可能为零

D．B沿A的斜面下滑时突然受到一沿斜面向上的力F的作用，当力F的大小满足一定条件时三角形木块A可能会开始滑动

利用本文的方法，可以避免大量重复的受力分析，且不难得出，答案应是：A、B。

(作者单位：浙江省东阳市第二高级中学)

【答案】C

【拓展】2012年新课标高考中的三个抛体运动的比较引出了很多的试题，在练习和检测中屡见不鲜，为此我们抽出典型模型进行分析比较。

同一水平直线上不同位置水平抛球并相遇抓住相同点：竖直方向运动情况相同；比较不同点：水平方向位移小，初速度小。要相遇，同时抛同一地点的不同高度处水平抛球抓住相同点：水平位移相同；比较不同点：竖直运动时间不同。要相遇，甲以更小速度先抛从相同高度同时水平抛出抓住相同点：高度相同；抓住关联点：AB水平位移之和不变

若第二张图是抛篮球运动，可以利用可逆性，将其视为反向平抛运动处理。

【变式】(2017·湖北华师一附中等八校联考)如图1所示，x轴在水平地面上，y轴沿竖直方向。图中画出了从y轴上不同位置沿x轴正向水平抛出的三个小球a、b和c的运动轨迹。小球a从(0，2L)抛出，落在(2L，0)处；小球b、c从(0，L)抛出，分别落在(2L，0)和(L，0)处。不计空气阻力，下列说法正确的是

( )

A．a和b初速度相同

B．b和c运动时间相同

C．b的初速度是c的两倍

D．a的运动时间是b的两倍

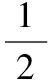
【答案】BC

二、单体平抛运动的功能结合

【例2】(2014·全国卷Ⅱ)取水平地面为重力势能零点。如图2所示，一物块从某一高度水平抛出，在抛出点其动能与重力势能恰好相等。不计空气阻力。该物块落地时的速度方向与水平方向的夹角为

( )

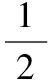
【答案】B

【例3】(2017·全国卷Ⅱ)如图3所示，半圆形光滑轨道固定在水平地面上，半圆的直径与地面垂直，一小物块以速度v从轨道下端滑入轨道，并从轨道上端水平飞出，小物块落地点到轨道下端的距离与轨道半径有关，此距离最大时，对应的轨道半径为(重力加速度大小为g)

( )

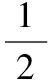
【答案】B

【点评】曲线运动与功能规律结合是新课标高考命题的热点之一。在2016年新课标2份试卷中，抛体运动、圆周运动以及功能规律的结合问题都是以压轴题形式出现，这种多过程问题利于考查学生对复杂过程的分析综合能力，利于不同层次的学生得到对应的分值，所以成为命题的热点。2017年的这道题还融入了数理结合知识，这种内容在最近几年的命题中比较常见，要高度重视，并用小专题熟悉理解。

三、单体平抛运动的受限问题

【例3】(2015·全国卷Ⅰ)一带有乒乓球发射机的乒乓球台如图4所示。水平台面的长和宽分别为L1和L2，中间球网高度为h。发射机安装于台面左侧边缘的中点，能以不同速率向右侧不同方向水平发射乒乓球，发射点距台面高度为3h。不计空气的作用，重力加速度大小为g。若乒乓球的发射速率v在某范围内，通过选择合适的方向，就能使乒乓球落到球网右侧台面上，则v的最大取值范围是

( )

【答案】D

【拓展】单体平抛运动的受限问题示例

斜面上的平抛问题半圆内的平抛运动平抛运动物体巧遇曲面x=v0t，y=12gt2，tanθ=yxvx=v0，vy=gt，tanθ=v0gth=12gt2，R±R2-h2=v0th=12gt2，Rsinθ=v0t，tanθ=vyv0=gtv0构建位移三角形构建速度三角形构建空间三角形构建速度三角形

【变式】一位网球运动员以拍击球，使网球沿水平方向飞出。第一只球飞出时的初速度为v1，落在自己一方场地上后，弹跳起来，刚好擦网而过，落在对方场地的A点处。如图5所示，第二只球飞出时的初速度为v2，直接擦网而过，也落在A点处。设球与地面碰撞时没有能量损失，且不计空气阻力，求：

(1)网球两次飞出时的初速度之比v1∶v2；

(2)运动员击球点的高度H、网高h之比H∶h。

【解析】(1)第一、二两只球被击出后都做平抛运动，由平抛运动的规律可知，两球分别被击出至各自第一次落地的时间是相等的

由题意知水平射程之比为：x1∶x2=1∶3

故平抛运动的初速度之比为v1∶v2=1∶3。

综合可得v1t2+v2t2=2v1t1

故t1=2t2，即H=4(H-h)

解得H∶h=4∶3。

(作者单位：江苏省江阴市江阴初级中学)