基于ANSYS零阶方法的海上风机单桩基础优化分析

胡丹妮+莫鋈+彭芬+严谨

摘 要：采用ANSYS有限元软件模拟了某海上风机单桩基础，考虑风、波浪、海流等环境荷载的共同作用对风机基础进行了拟静力分析，基于ANSYS零阶优化方法对桩基尺寸进行了优化。在保证位移、应力及稳定性要求的前提下，减小了桩基壁厚，优化后使桩基的总体积减小了33.4%，达到了轻型化设计目的；结合优化过程中目标函数、设计变量和状态变量的变化规律，提出了桩顶位移是优化设计的主要限制条件，结构设计时可以考虑进行形状拓扑优化；在保证桩顶位移的情况下，可以适当减小桩基础某些地方的壁厚，使材料的强度得到充分的利用。

关键词：海上风机 单桩基础 零阶优化方法 尺寸优化

海上风力发电作为当前提倡的低碳经济发展项目之一，近几年在我国发展十分迅猛。与陆上风力发电相比，它所处的海洋环境十分复杂和恶劣，是高风险投资的项目，如何降低海上风电成本是当前乃至今后海上风电发展的主要目标。根据相关资料显示，基础成本约占整个风电场工程成本的15%～25%，因此设计安全、合理且经济的基础成为降低开发海上风电资源成本的关键问题之一。

关于海上风机相关研究国外学者做得较多，由于造价低、施工方便等特点，目前，海上风机单桩基础得到了广泛应用，Yoon G等采用响应曲面法对海上风电单桩基础进行了可靠性分析；Agarwal P等通过相关研究，提出利用结构可靠度原理可以提高海上风机设计计算效率；Torcinaro M等考虑海上风机支持结构对应的环境荷载极限状态，提出了一个初步设计的优化过程；Bontempi F通过数值模型的建立，对海上风机在复杂环境下安全性能进行了评价，较好的指导了结构设计。国内学者康海贵等通过研究推荐了一種基于可靠度的海上风机基础优化设计方法，后期还借助有限元软件对风机基础与上部灌浆连接段进行了优化；郇彩云对海上风机桩基结构设计进行了研究；按照设计规范要求，我国海洋平台结构采用重复“试算—验证—修改”设计方法进行，需要消耗大量的人力资源和设计时间，所得到的设计方案也不一定是最好的或最优的，在海上风电场的设计过程中需要引入一个有力的辅助工具进行优化设计，严云对基于ANSYS参数化设计语言的结构优化设计方法进行了研究；ANSYS零阶优化方法已在机械结构尺寸优化方面得到了应用。基于此，本文以ANSYS零阶优化方法为理论基础，采用ANSYS有限元软件，对海上风机单桩基础进行了尺寸优化，并对优化结果进行了分析。

1.ANSYS零阶方法原理

零阶方法仅需要因变量的数值，而不需要其导数信息。在零阶优化方法中目标函数及状态变量首先通过最小二乘拟合近似值；然后将有约束的优化问题用罚函数转换成无约束的优化问题，优化过程在近似的罚函数上进行迭代，直至获得收敛解。因此，该方法属于直接法，可以有效的处理大多数的工程问题。ANSYS零阶方法建立在目标函数及状态变量的近似基础上，在设计初期需要一定的初始设计变量数据，初始数据可以根据其它优化工具和方法直接生成，或随机生成。零阶方法在初始数据中进行一定次数的抽样，拟合因变量和目标函数的响应函数，从而寻求最优解，故又可称其为子问题方法。

优化问题求解时，近似化处理目标函数与状态变量公式，将有约束的问题通过罚函数转换为没有约束的问题再进行优化，即零阶方法式：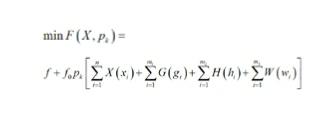

式中：xi—设计变量；gi、hi 、ωi—状态变量；X（xi）—与设计变量对应的罚函数；G（gi）、H（hi）及W（ωi）—与状态变量对应的罚函数；F （X，Pk）—响应面函数，与设计变量和响应面参数相关；f 表示目标函数；pk—响应面参数。

每个迭代中，采用SUMT方法，即一种系列无约束优化技术来计算F（X，Pk）。其中：k对应子问题求解时的子迭代，为尽量保证收敛结果的精确性，pk在数值上将随着子迭代的增加而增加。所有罚函数均采用由内伸张型，转化为无约束问题后，即可采用序惯无约束优化方法来搜索无约束目标函数。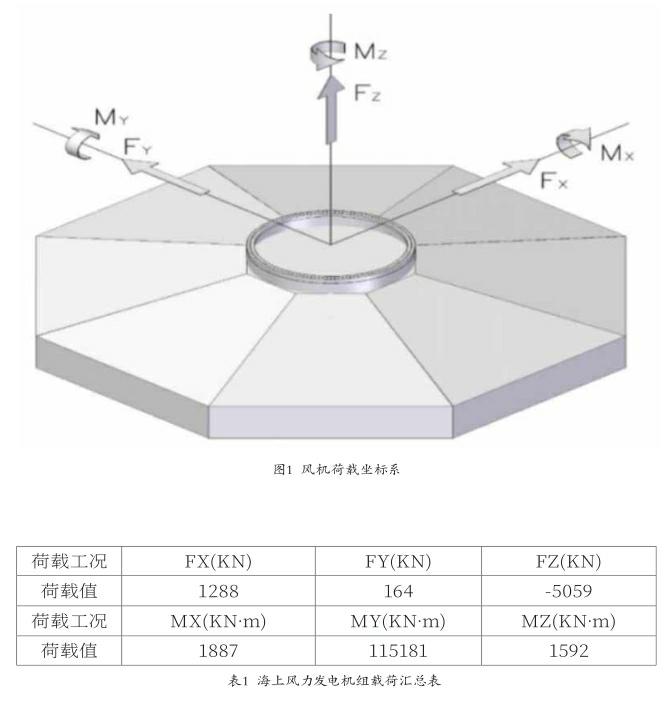

2.模型建立与优化

2.1荷载条件

按照风机承载能力极限工况对海上风机单桩基础进行加载，并考虑了1.35的安全系数，以集中荷载的形式加载在塔架底端法兰处。作用在塔架底端的风机荷载坐标系如图1所示，风机承受的荷载情况见表1。其它环境荷载直接利用Pipe59单元自带的水流参数表格自动模拟，其中，波浪荷载按照Stokes五阶波理论进行模拟。

2.2模型建立

常见海上风机桩式基础包括单桩基础、单立柱三桩和导管架基础等结构型式，本文主要对单桩基础进行有限元仿真建模及优化分析。文中的单桩基础采用钢管桩，经过试算得到满足规范要求的风机初始尺寸如表2所示：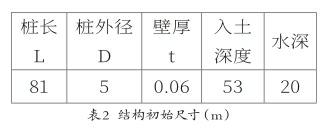

以往研究表明，对浸没在海水中的构件所承受的波浪、海流等荷载的作用力，可以采用ANSYS程序中的PIPE59单元进行模拟，效果较好。海上风机的桩基础可分为水面以下及以上两部分，后者又包括嵌岩部分及水浸部分，其中嵌岩部分桩基采用PIPE16单元模拟，水浸部分采用PIPE59单元模拟。采用P-y曲线来反映桩—土之间的相互作用关系，并利用Combin39单元来模拟，因为桩土相互作用的研究是一个比较复杂的问题，所以对于桩土关系不做详细研究，为了简化计算，考虑桩基底端是固定的。结构的简化模型与有限元模型如图2所示。

2.3优化过程

基于ANSYS零阶优化方法，采用ANSYS参数化设计语言（简称APDL）来实现优化设计，基本参数包括：设计变量（Design Variable简写为DV）、状态变量（State Variable 简写为SV）、目标函数（Objective Function）三个基本要素。在静力求解结束后的后处理模块中，可创建状态变量和目标函数。在单桩基础尺寸优化的过程中，以桩径 D和桩壁厚t为设计变量，以桩结构总体积 V最小为目标函数。约束条件包括强度约束（应力σ、τ）、刚度约束（位移U）、稳定性约束（细长比 λ）和几何约束（桩径D及壁厚t），强度、刚度和稳定性约束均按照结构设计规范中的具体规定处理，几何约束即为设计变量的上、下限。进行优化计算的数学模型如下：endprint

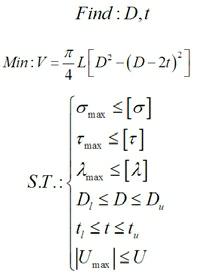
式中：D—桩基外径；t—钢管桩壁厚；V—总体积；L—桩长；σmax、[σ]—桩身中最大正应力及结构容许正应力；τmax、[τ]—桩身最大切应力及结构容许切应力；λmax—桩身最大长细比；Du、Dl—桩身外径上下限；tu、tl—桩基壁厚上下限；Umax、U—桩顶的最大位移及其上限。

2.4优化结果分析

优化结束后，优化前、后的相关参数值对比结果如表3所示。很显然，优化以后桩基础的的设计尺寸发生了变化，截面面积也减小了，最优结果主要是在确保位移、应力以及稳定性的要求的前提下，减小了桩的壁厚，最终使得桩身的重量达到轻型化的目的。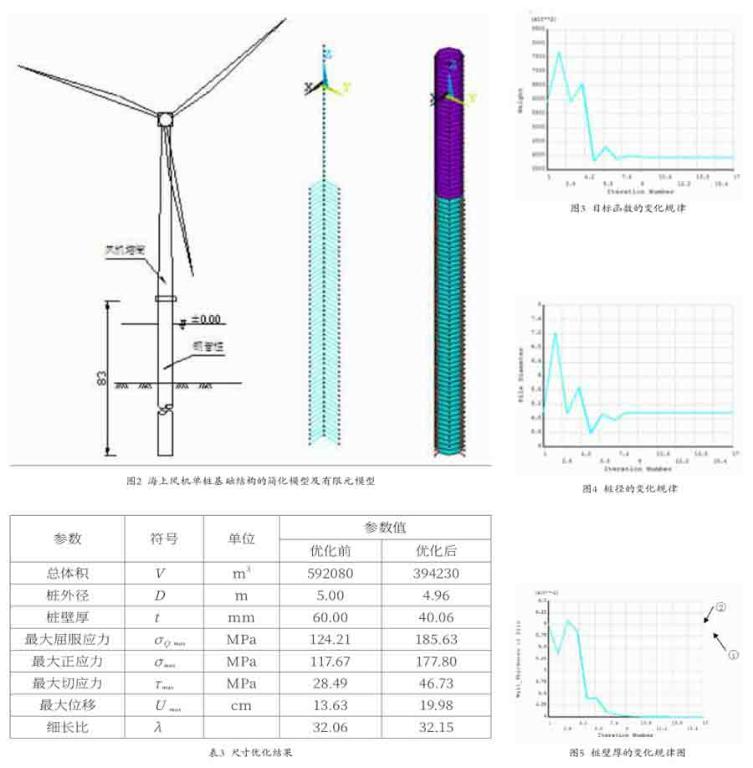

表3的结果显示：优化前后，桩基础的桩径并未发生明显的变化，因此，有必要研究一下优化过程中各参数的变化情况。目标函数、设计变量DV（包括桩径和桩壁厚）及状态变量SV（包括桩身应力、桩顶最大位移和细长比）等参数在优化过程中随迭代次数的变化规律如图3-8所示。

将优化前的设计变量代入目标函数进行迭代计算，可以找到系统默认的桩身最小体积，由图3-5的变化规律可以看出，迭代7次后目标函数计算曲线趋于平稳，对应的桩径、桩壁厚也达到了系统默认的最优状态，桩壁厚减小了近20mm，桩基的總体积减小了33.4%。

图6包括三条应力曲线，其中①代表最大屈服应力，②代表最大正应力，③代表最大切应力。在迭代计算初期，桩身应力较小，材料没有充分利用，随着迭代次数的增加，最大屈服应力及最大正应力都得到了提升，且始终保持在其容许应力范围内；图8反映的桩身细长比也充分满足桩身的稳定性要求；但图7的桩顶位移变化情况显示，迭代计算4次时出现桩顶位移最大值，已经超出桩顶容许位移的上限，之后的计算结果也都临近容许值。迭代计算结果表明：对单桩基础进行7次迭代计算以后，目标函数基本可以达到系统默认的优化值，各状态变量也得到了表3中优化后的结果，在优化的三组状态变量中桩顶位移是最为主要的限制条件。这主要是由于在海上风电场中，桩基础所支撑的是上部高达70～120m左右的塔筒及风机主体，桩顶微小的位移都会在风机机舱处放大几十倍，所以为了保证风机的正常运行，桩基顶端的位移必须限制在很小的范围内。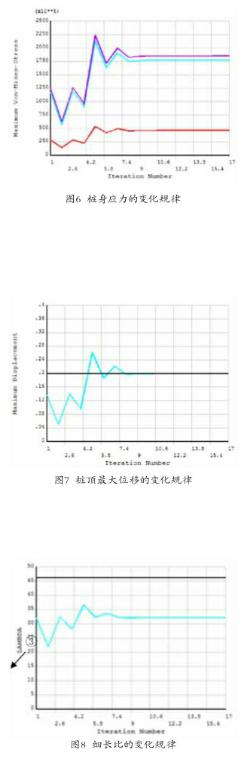

3.结论

设计安全、合理且经济的基础是降低开发海上风电资源成本的关键问题之一。本文通过建立海上风机单桩基础的优化模型，并基于ANSYS零阶优化方法对桩基尺寸进行了优化研究分析，结合优化结果可以得出：

（1）在确保位移、应力及稳定性要求的前提下，通过对风机桩基础的尺寸优化，减小了桩基壁厚，使得目标函数（桩基的总体积）减小了33.4%，经济效果十分可观，且达到了轻型化设计目的；

（2）桩顶的位移是优化过程中至关重要的约束条件，在风机设计时，可以考虑对基础进行形状的拓扑优化，在保证桩顶位移的情况下，适当减小桩基础某些地方的壁厚，使其材料的强度得到充分的利用。

[基金项目：广东海洋大学“创新强校工程”省财政资金支持项目（GDOU2017052503）。]

参考文献：

[1]Yoon G，Kim S，Kim H.Reliability analysis of monopole for offshore w i n d f o u n d a t i o n s u s i n g t h e response surface method[J]，New F r o n t i e r s i n G e o t e c h n i c a l Engineering， 2014：108-117.

[2]Agarwal P，Manuel L.Reliability analysis and design procedures f o r o f f s h o r e w i n d t u r b i n e s[J]，Structures Congress，2008：1-9.

[3]Torcinaro M，Petrini F， Arangio S . St r u c t u r al o f f s h o r e w i n d turbines optimization[J]，Earth and Space，2010： 2130-2142.

[ 4 ] B o n t e m p i F . A d v a n c e d t o p i c s i n o f f s h o r e w i n d t u r bin e s d e sign [J] ，Ea r t h an d Space，2010：1981-1991.

[5]康海贵，李玉刚，郇彩云.基于可靠度的海上风机基础结构优化设计方法研究[J].太阳能学报，2009，30（12）：1602-1607.

[6 ]康海贵，孙道明，莫仁杰，等.海上风机桩基础与上部结构灌浆连接段优化分析[J] ，沈阳建筑大学学报（自然科学版），2013，29（1）：77-85.

[7]郇彩云.海上桩式风机基础结构设计与研究[D].大连：大连理工大学，2009.

[8]严云.基于A N S Y S参数化设计语言的结构优化设计[J ] .华东交通大学学报，2004（8）：52-54.

[9]吴荣，王晓平，苟敦攀，等.基于ANSYS零阶方法的塔式起重机塔身结构优化设计[J]，设计计算，2014，45（2）：42-46.endprint