层次分析法和模糊矩阵法在绩效考核中的应用

尤兴华

（南京工程学院，江苏 南京211167）

绩效：相对于教师，是考评其工作表现、行为及其结果；相对于学校，是指任务在教学数量、教学质量和教学效率等方面完成的情况.考核绩效，利于制定人事决策与措施，利于调整和改进学校的效能.学校教师绩效考核的量化过程的处理是考核实施过程中的关键.下面的案例是5个评委利用8项评价指标，对某大学2007年教师进行绩效考核，主要参照上半年的绩效考核数据.限于篇幅，而不失一般性，本文选择某部门11个人进行绩效考核研究.

1 基于层次分析法的模型

为使模型相对精确，解决步骤如下：（1）5个评委打分；（2）加权平均，算出11个教师8个指标的平均成绩；（3）采用层次分析法 （AHP）［1］以及模糊一致矩阵法确定比较权重，量化绩效考核；（4）适当补充，完善考核的指标；（5）继续使用层次分析法确定考核因子的权值；（6）建立模糊综合评价模型.

注：（1）由于牵扯到学校内部资料，本文中只会将所用到的数据罗列出来，其他数据不会出现.（2）层次分析法具体理论及基本步骤详见参考文献［1、2］.（3）层次分析法与模糊矩阵法解决各类问题的文献很多［3～10］，说明具有研究的价值.

1.1 层次分析法的相关指标

决策问题分解为3个层次：目标层 （上层），准则层 （中层），方案层 （下层）.通过比较各准则对于目标的权重，及各方案对于每一准则的权重，将下层对中层的权重及中层对上层的权重进行一定综合，确定下层对上层的权重.计算出关于总目标优先度相对量度，排出优先顺序，从而为选择最优方案的决策.

如何比较同一层各因素，以及对上层因素的影响，从而确定它们在上层因素中所占的权重呢？

假设某一层共有n个因素C1，C2，…，Cn，它们对上层一个因素O有影响，需要每次取两个因素Ci和Cj，为了方便现在使用aij表示Ci和Cj对O的影响之比.它们的比较结果表示为：

成对比较矩阵

其中 （1）式中的A称为正互反矩阵.

这里，A可能是一致矩阵［11］，但也有可能不是一致阵.必须注意：如果不一致，在容许范围内Saaty等人用对应于A最大特征根λ的归一化后的特征向量w作为权向量，这里w满足

比较尺度：相对尺度aij，用Saaty等人提出的1～9尺度，即取1，2，…，9，其互反数即1，1／2，…，1／9.

一致性检验：Saaty定义为一致性指标：

其中CI＝0时，A为一致阵；CI≠0时A为不一致阵，CI越大，A的不一致程度越严重.确定A的不一致程度的允许范围.Saaty又引入所谓随机一致性指标RI，以便找出衡量A的一致性指标CI的标准.对于成对比较矩阵A：当n＝1，2时，RI＝0；当n≥3时，Saaty引入一致性比率CR，它由一致性指标CI与同阶的随机一致性指标RI之比表示，其中

k为矩阵A最大特征值平均值，当CR＜0.1时，可用其特征向量作为权向量.

1.2 数据预处理

现有组装车间中的11个教师，根据8个指标来比较这11个人.

8个指标分别为：职称、个人努力、教学质量、教学论文、科研论文、教材、基金、其他.

5个评委根据以上指标对教师打分，按照前文步骤，求得其平均得分值如下：p1＝ （7.8，8，8，8，8，7.4，8，7.4）；p2＝ （6.4，6.8，6.6，5.8，7.2，6.6，7，7.4）；p3＝ （6.8，7，6.2，5.8，6.4，5.2，5.6，6.4）；p4＝ （6.6，7，6.6，6，6.2，6.6，6.6，7）；p5＝ （7，6.6，6.4，6.8，7.4，7.4，7.2，7）；p6＝ （7.2，6.6，6.4，6.8，7.8，7.2，7.2，6.8）；p7＝ （7.8，6.8，7.6，7.2，7.6，7.6，7，7.4）；p8＝ （7.2，7.4，7，6.8，7.4，7.2，7，6.8）；p9＝ （8.6，8，8.2，7.4，8.2，7.4，8.2，7.8）；p10＝ （8.4，7.8，8.2，7.2，7，7.6，8.2，7.8）；p11＝ （8.2，7.6，8，7.6，8，8，7.6，7.8）.

1.3 AHP模型的建立

在进行绩效考核时，根据8个准则在学校发展中所占比重，选取影响学校发展的那些准则［4］.

通过比对，职称、教学质量、科研论文这3个指标比较看重.其次通过每一个准则进行对比，根据个人突出的地方，最后进行综合判断，确定出绩效成绩的先后顺序［1］.

三个层次分别为：目标层——绩效考核；方案层——pi（i＝1，…，11），11个选择；准则层——8个准则，见表1：

根据指标重要性，形成正互反矩阵：

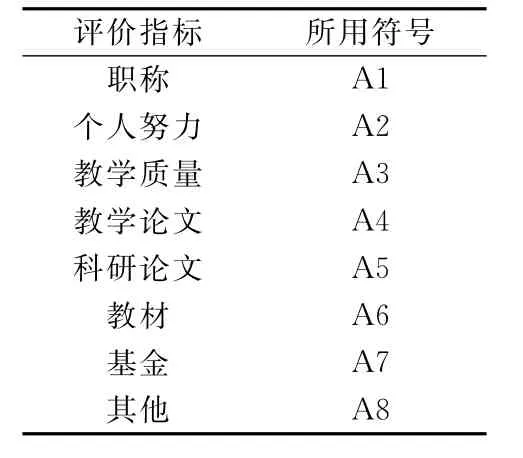
表1 绩效考核指标体系

利用Matlab，算出正互反矩阵A的特征值λ＝8.684 126 988，对应的特征向量

w＝ （0.358，0.095，0.141，0.079，0.079，0.046，0.133，0.070）T

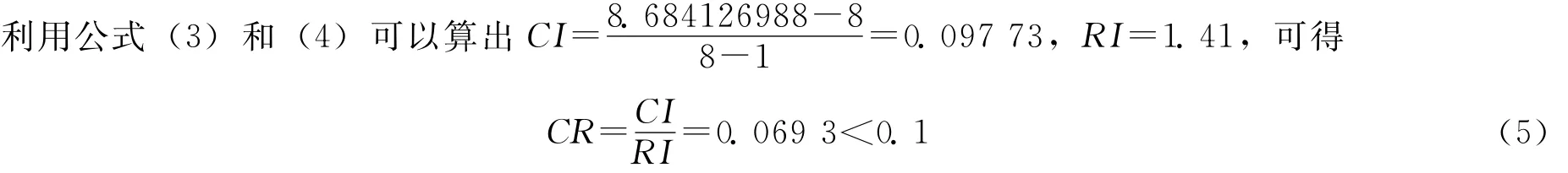
则CR＜0.1，符合一致性检验，这里特征向量w可作为权向量.

在绩效考核问题中已经得到第二层对第一层的权向量，同理可构造第三层对第二层的所有准则的所对应的成对比较阵，因为矩阵较多，限于篇幅，以第一个矩阵为例，其余的矩阵省略.

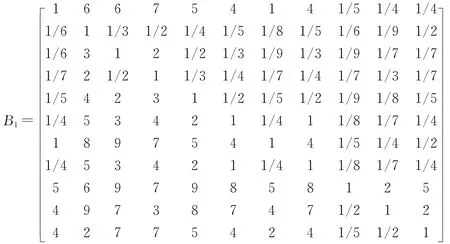
1.4 计算数据

用刚才的Bk计算出权向量w（8）k以及相应的最大特征根λk，数据见表2：

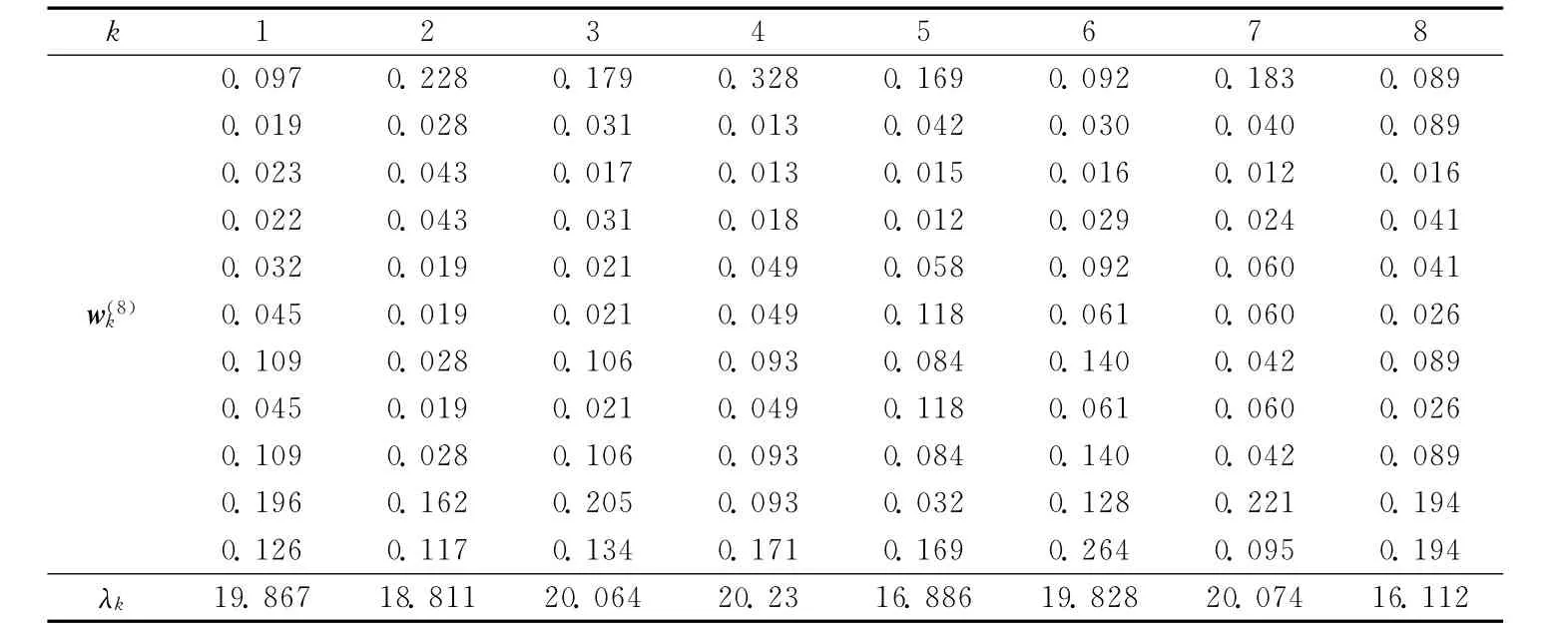
表2 绩效考核问题第3层的计算数据

利用Matlab以及文献 ［1］中方法，求出方案在目标中的组合权重：

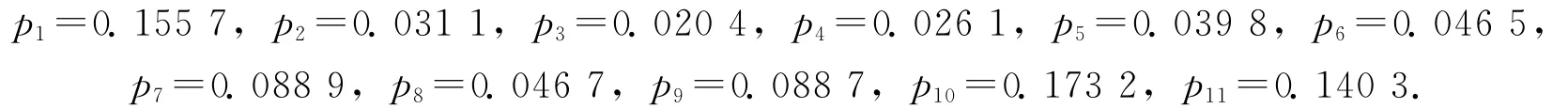
得出这11个人考核顺序为：

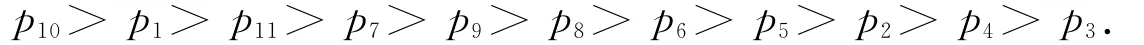
2 基于模糊一致矩阵法的模型

模糊一致矩阵法具体理论及基本步骤详见参考文献［1～3］.

2.1 相关参数

（1）多目标决策问题有n个目标Ok；

（2）指标Rk；

（3）m个决策方案Ai（i＝1，…，m）；

教师设情境置2：假如在等待“120”过程中，你发现晕倒的女生又被刮伤出血了，该怎么办？阅读教材76页第二段。如何根据出血状况，判断出血类型？请阅读教材86页。

（4）模糊优先关系矩阵B＝ （bij）m×m，其中bij＝1表示Oi比Oj要重要；bij＝0.5表示Oi与Oj同等重要；bij＝0表示Oj比Oi要重要.

（5）模糊一致矩阵F＝ （fij）m×m其中

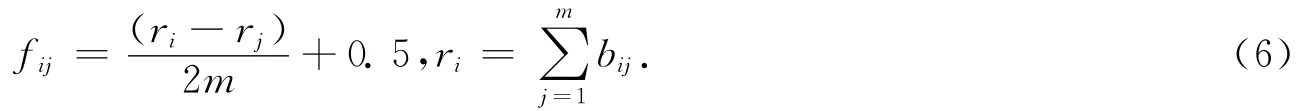
（6）权重wk（k＝1，…，n）

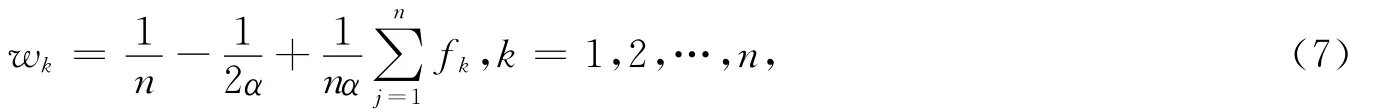
其中：α应满足α≥ （n－1）／2.

2.2 多目标决策方案优先过程的实现

实现步骤如下：

（1）建立优先关系矩阵：

因为是m个方案Ai（i＝1，…，m）在n个目标Ok下的优选问题，因此可得n个矩阵

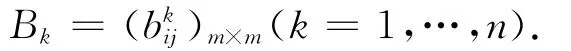
（2）将矩阵Bk＝（k＝1，…，n）改造成模糊一致矩阵

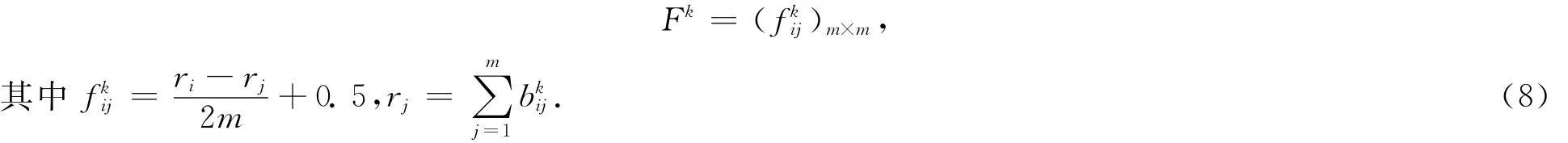
（3）单目标排序.

运用方根法计算方案Ai在目标Ok下的优度值ski，

（4）多目标总排序.

在（3）基础上，计算总体优度值

对诸方案进行总体排序（按大小），即如果Ti1≥Ti2≥…≥Tim，那么有从优到劣的顺序Ai1≥Ai2≥…≥Aim.

2.3 模型的建立

在本文所研究的问题中，有11个人选pi（i＝1，…，11），在8个指标ui（i＝1，…，8）的衡量下［8］，结果如表3所示：

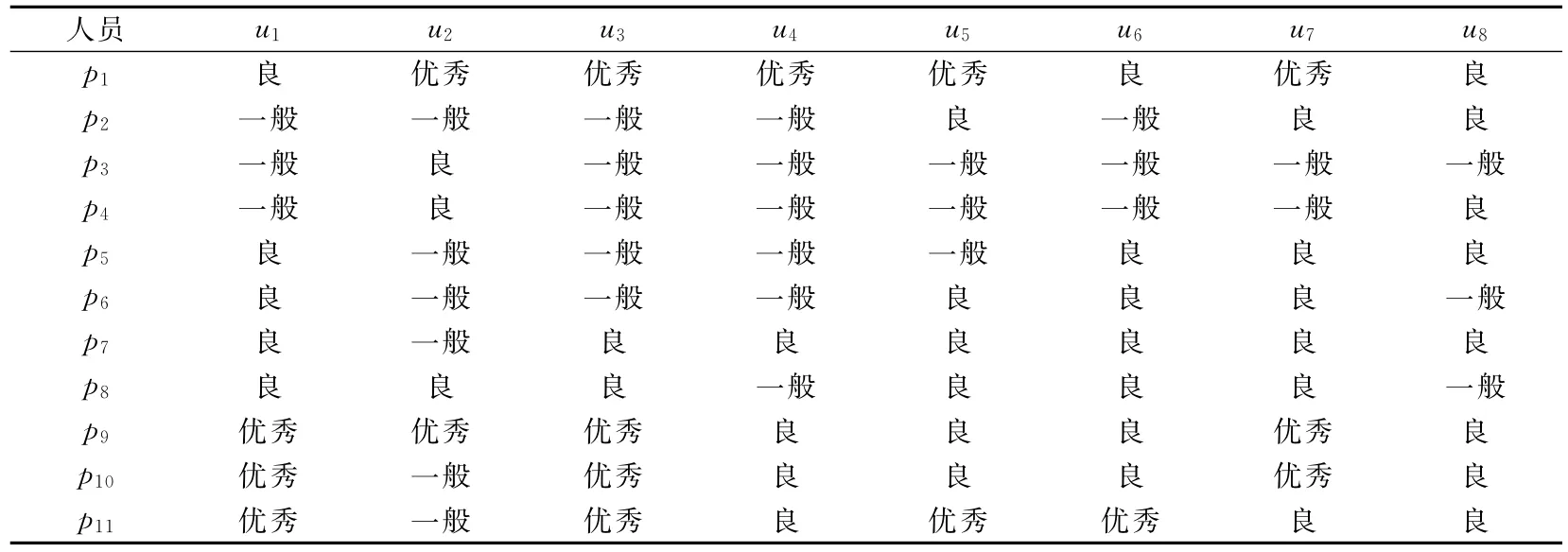
表3 模糊判断矩阵表

由前面数据标度，定义“优秀”、“良”、“一般”之间的相对优先程度数量标度如表4所示.

下面讨论确定评价指标对绩效考核影响的权重.按照学校实际经验可知，8个评价指标中u1最重要，u2第二重要，u3可认为第三重要，u4、u5、u6、u7、u8是同等重要的，则可建立

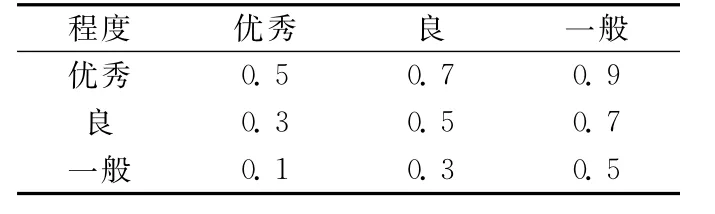
表4 相对优先程度优先数量标度表

评价指标的优先关系矩阵［9］

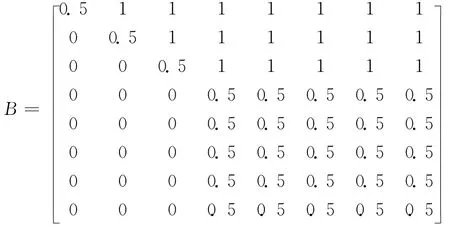
将模糊优先关系矩阵B改造成模糊一致关系矩阵F，具体如下：

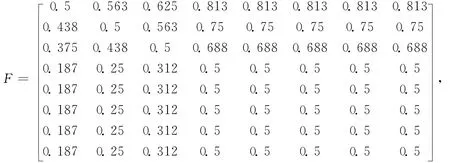
计算各权重α＝ （8－1）／2＝3.5则

进行优先排序，建立模糊关系矩阵，由于矩阵很多，现在只列出第一个模糊关系矩阵，其余矩阵省略：

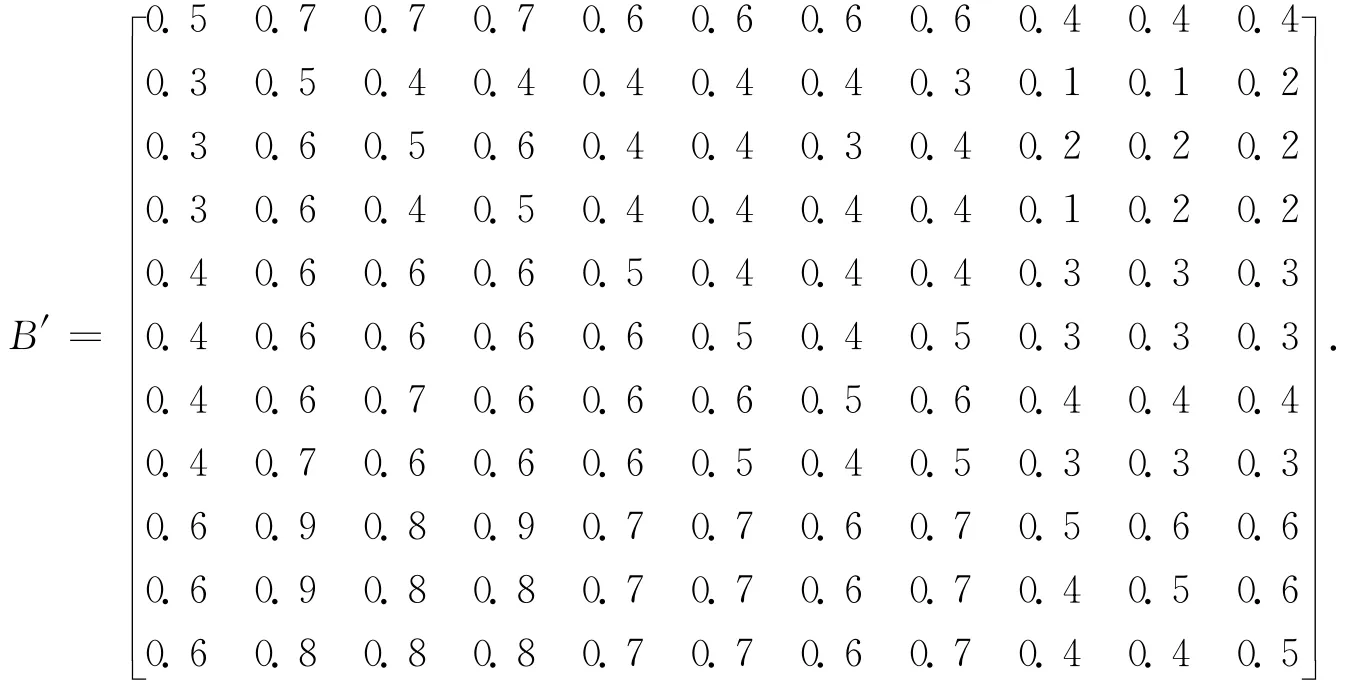
然后将关系矩阵改造成模糊一致矩阵，第一个见下面：

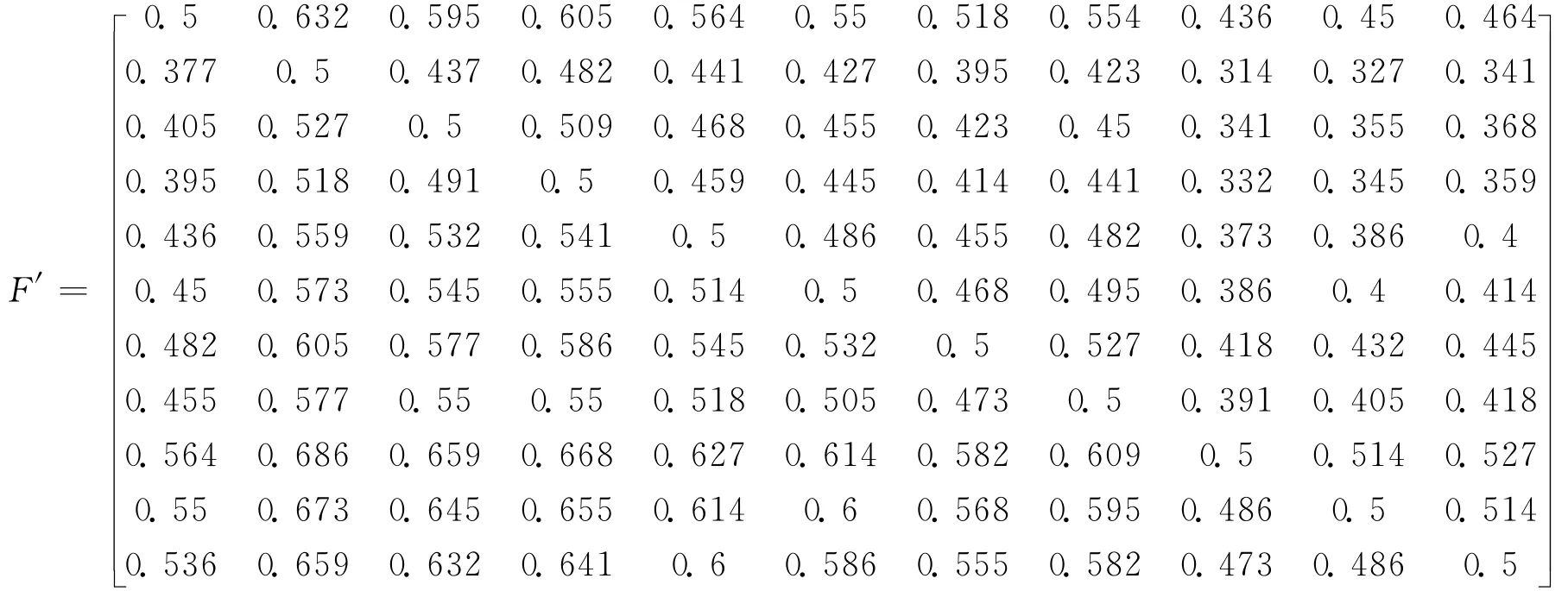
其余的模糊一致矩阵省略.

2.4 具体的计算

进行单目标排序，得到结果如表5所示.

进行多目标排序：

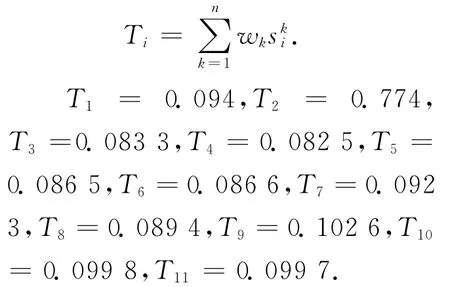
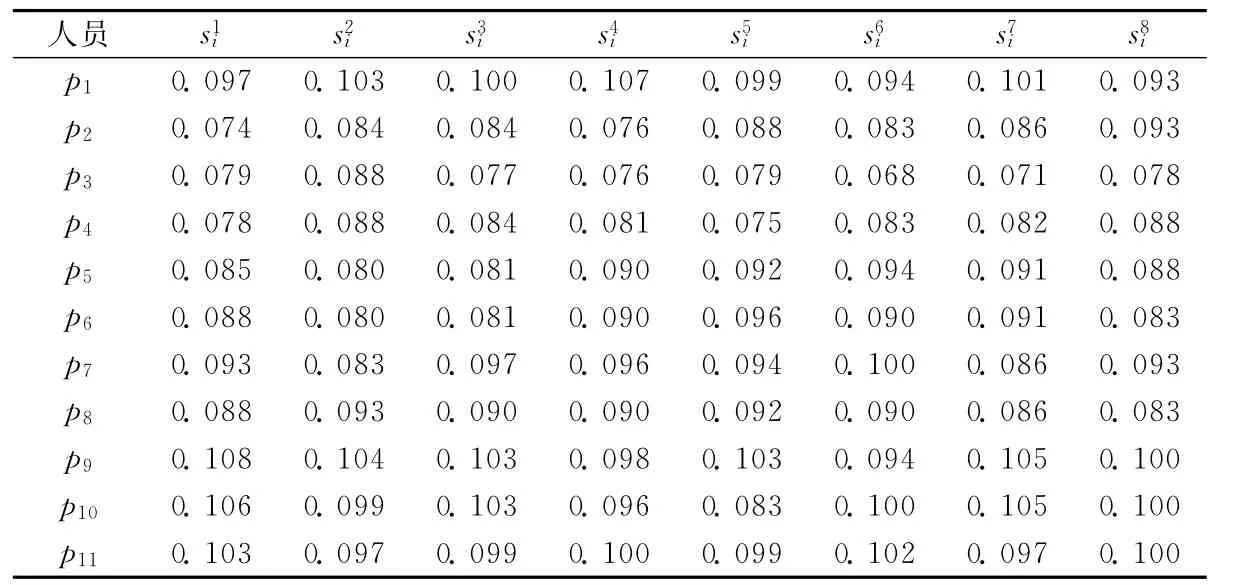
表5 方案优度值表

由此可以得出这11个人的绩效考核的先后顺序为T9＞T10＞T11＞T1＞T7＞T8＞T6＞T5＞T3＞T4＞T2.

3 相关结论

比较两种分析法，可以发现11人绩效排名有一些差异，层次分析法中排列如下：

p10＞p1＞p11＞p7＞p9＞p8＞p6＞p5＞p2＞p4＞p3，

模糊一致矩阵中排列如下：

T9＞ T10＞ T11＞ T1＞ T7＞ T8＞ T6＞ T5＞ T3＞T4＞ T2.

出现这种情况的原因：

（1）前者，在计算矩阵的最大特征值及对应特征向量时，利用了一致性指标、随机一致性指标以及一致性比率，并且做一致性检验.如果检验通过，那么特征向量可作为权向量，反之，则必须重新构造成对比较矩阵.实际案例中，有时要想一次通过检验的成对比较矩阵，需要在原始矩阵上进行一些必要的改动，致使数据会与原始数据产生误差.但AHP法在处理复杂问题时有它的可取之处，所得结果比较精确.

（2）后者，则不需要进行一致性检验，很大程度上保留了原始数据，但是，并没有层次分析法那样的精确，不能很好地体现出被评价者之间的差距.