虹吸式出水管体型优化设计研究
谭淋露,孙 杨
(1.江西省水利科学研究院,江西 南昌 330029;2.江西省水利职业学院,江西 南昌 330013)
虹吸式出水管体型优化设计研究
谭淋露1,孙 杨2
(1.江西省水利科学研究院,江西 南昌 330029;2.江西省水利职业学院,江西 南昌 330013)
在数值模拟基础上,利用神经网络算法对虹吸式出水管进行体型优化设计,得到了参数与优化目标之间的最优解集,优化方案解集相较于原方案,在虹吸性能和管内流态方面均有明显改善,可为虹吸式出水管设计提供参考。
虹吸式出水管;神经网络;数值模拟;水力优化设计
虹吸式出水管能够安全可靠地切断泵站出流,避免机组长时间倒转,因而应用广泛。在目前的虹吸式出水管参数设计中,大多根据经验推定取值,或是参考已有的规模相近且水力性能较好的管道形线,缺乏系统的设计依据。
本文基于数值模拟,利用SPSS Clementine内部的Exhaustive Prune神经网络模型对虹吸式出水管的主要设计参数进行了探讨,以虹吸形成时间与虹吸稳定后的水力损失为指标进行量化分析,综合研究成果,对虹吸式出水管管道体型设计提出优化方法[1-8]。
1 神经网络算法概述
人工神经网络是一种通过模拟脑神经细胞的结构实现复杂信息处理的人工智能技术。它具有自组织、自学习、能够分布并行处理及推理等特性,因而广泛应用于控制优化、故障诊断等领域。
如图1所示,人工神经网络利用物理器件来模拟生物神经网络的结构和功能。中间的圆形部分模拟的是我们人脑中神经元的中心——细胞体;在细胞体前有一个神经元的主要接收器,模拟的是脑神经元中的“树突”,用来接收信息;在细胞体后的是用来传导信息的“轴突”,轴突的末端与另一个细胞体或其树突构成一种突触的整体,从而通过突触实现神经元间信息的传递。
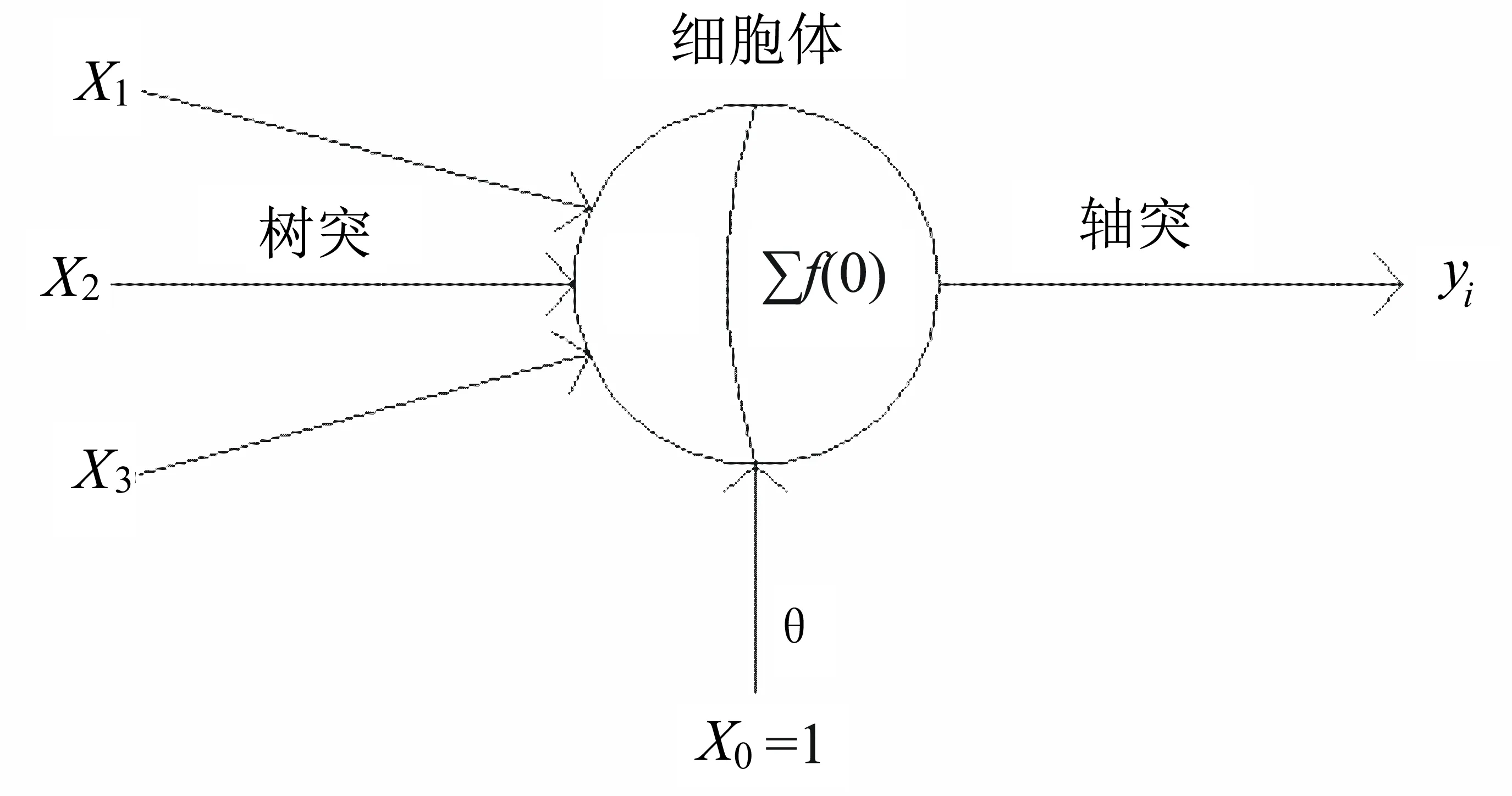
图1 典型人工神经元模型
大量人工神经元组成的拓扑结构即图2的神经网络模型。在神经网络中的处理单位可以分成一层层的不相交的子集,每一层的神经元在传递函数的过程中有3种形式:一是输入层:只接受信息的输入;二是输出层:将信息输出,此输出可能直接影响整个系统,也可能只影响系统外的其他系统;三是隐含层:信息的输入与输出都在系统中的单元。输入层接收从外部环境到达信息的输入,产生输出,而后此输出被用于隐含层的输入,这个过程一直持续到满足了某个特定条件进而输出到外界环境。
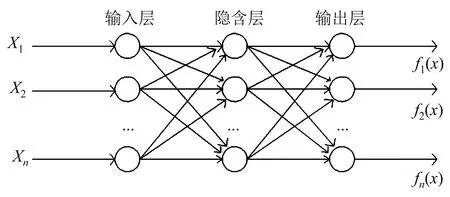
图2 典型神经网络模型
SPSS Clementine内部拥有高级建模技术,包含各种神经网络,极易操作理解,并且可视化性能好,是一款适合无编码基础的人员选择的软件。其中Exhaustive Prune神经网络算法是建立一个大型的神经网络,随着训练的进行修剪隐藏层和输入层。由于是彻底修剪,能够彻底搜索神经网络的内部空间,选出最好的模型,因而这种方法虽然较为缓慢,但常常生成的是最好的结果。
2 模型建立与模拟结果
2.1虹吸式出水管概况
虹吸式出水管的结构布置如图3所示,在管道的型线结构中,上升段上升角、驼峰断面高宽比、曲率半径与下降段下降角对水力特性影响较大,是本文的研究对象。
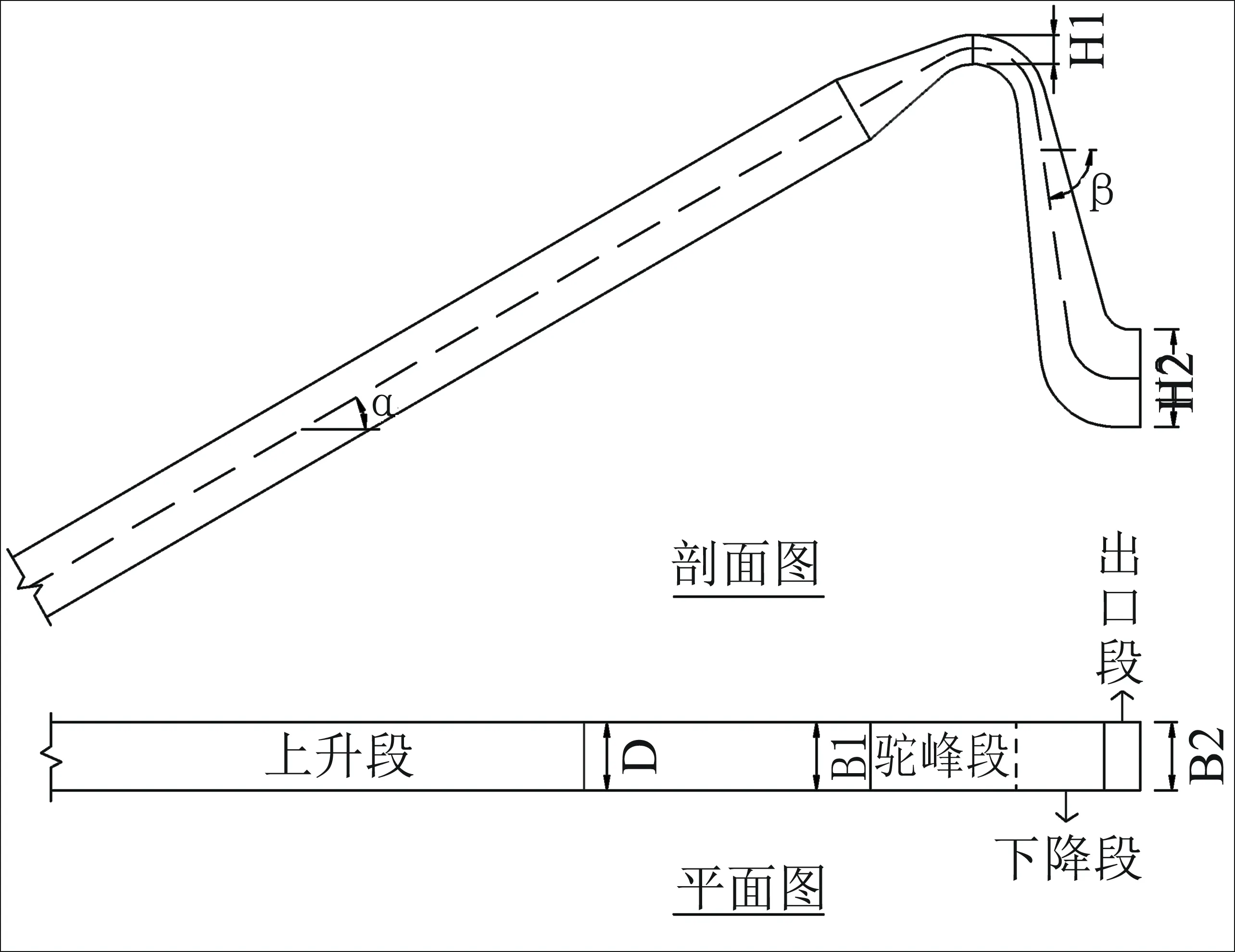
图3 虹吸式出水管管路模型
2.2计算模型
本文模拟的是水流进入管道,逐渐将空气排出,水流形成稳定虹吸的过程。在初始时刻,管内主体为空气,出水池中存有部分原始水体。模拟区域从水流进入上升段开始,至充满出口段后出水池结束。采用四面体单元进行网格划分,多相流模型混合模型,并采用了对弯曲流线运动支持较好的RNGk-ε进行数值模拟,采用SIMPLEC算法。进口边界采用速度入口条件,出水池水面以上大气进口设为压强出口,管道内部及出水池边壁设为壁面边界。用有限体积法对控制方程离散,将压力、湍动能、湍动能耗散率布置于控制体中心,速度矢量布置于控制体表面。采用压强速度耦合算法进行计算,选用SIMPLEC算法求解方程。
守恒方程为:
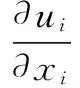
(1)
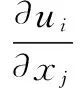
(2)
式(1)、(2)中:xi(i=1,2,3)为笛卡尔坐标系坐标;ui为速度矢量u在i方向的分量;gi为沿i方向的质量力;v为水的运动粘度系数;vt为涡粘性系数。
k-ε控制方程为:
(3)
(4)
其中:
μeff=μ+μt;
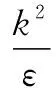
Cμ=0.0845,αk=αε=1.39;
C1ε=1.42,C2ε=1.68;
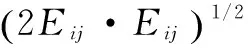
η0=4.377,β=0.012
2.3计算结果
2.3.1 虹吸形成过程 图4为数值模拟的虹吸形成过程图,水泵启动后,水流沿着管道上升段上升,管内气体受压挤向出口段水面,从出口段与出水池连接处排出。水流急剧翻越过峰顶后,快速下落,此时水气相互掺和翻滚剧烈,气体在水流的挟带下间歇性排出。随着空气的逐渐排出,驼峰气压逐步由正压转为负压,旋滚区逐渐减小,直至管内气体全部排出,虹吸形成过程完成。最终测得虹吸形成时间为36.3 s。
2.3.2 稳定后流态观测 在虹吸过程完全形成后,水流形成稳定虹吸。图5为均匀进水条件下,虹吸式出水管纵剖面水流流速图。从图5可知,上升段水流平顺,驼峰段由于管口缩小,流速增大,弯管部分因管道形状的变化流速以轴向流速为主,下大上小;下降段主流紧贴上壁,左下方存在脱流现象,尾部有较大范围的回流,流态较为紊乱;出口段流速稍有调整,但分布不均。这些局部的不良流态对管道的安全高效运行会产生不良影响,因此对其体型进行主要设计参数研究非常必要。
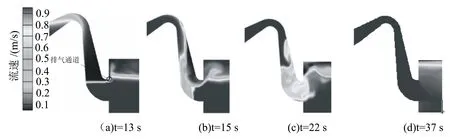
图4 虹吸形成过程图
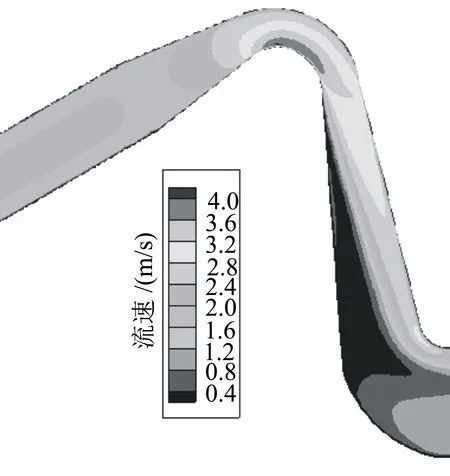
图5 虹吸式出水管纵剖面图
3 利用神经网络算法进行优化
3.1创建数据样本
采用SPSS 13.0软件中正交设计功能,在设计向导中输入参数和水平数,取得16组样本,通过流体动力学仿真,得到《正交实验结果》特征样本集用以训练神经网络。得到样本如表1所示。
同时,将其他可能的组合交互变化组成预测样本。

表1 正交实验特征样本及结果
3.2选择模型
如图6所示,采用SPSS Clementine中提供的Exhaustive Prune神经网络算法建立模型,将以上《正交实验结果》导入,分别以虹吸形成时间T权重与水力损失S权重为50%与50%、40%与60%、30%与70%、20%与80%、10%与90%作为目标建立Exhaustive Prune神经网络模型。
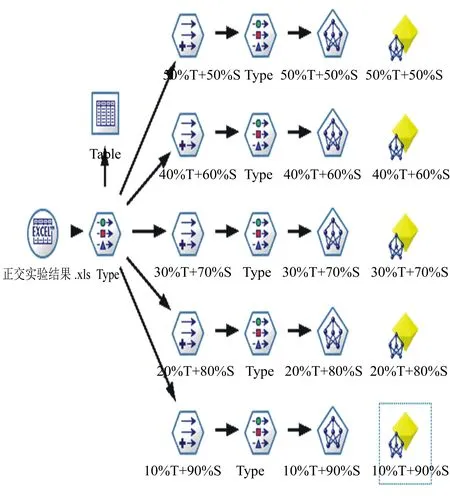
图6 神经网络模型建立设计图
如图7所示,将所建立的模型投入到预测样本中运行,对预测样本结果进行选择,即得到各优化目标下的优化结果,将5组优化结果对比取交集得到优化解集。
各优化解集中相同解汇集成表2,即虹吸式出水管的优化方案解集。
3.3优化结果验证
将得出的优化解集中的各优化方案进行数值模拟,分别得出各优化方案下虹吸式出水管的水流流动情况(图8)。

表2 优化解集
如图9、图10所示,在虹吸式出水管的各优化方案中,水流在上升段内流速分布均匀,流态较好;驼峰段由于管口逐渐缩小,流速加大,弯管部分流势明显,下大上小,均匀转向,且无原始设计方案中大于3.6 m/s的流速,说明流速均匀度有所提高;下降段虽仍存有脱流现象,但回流区较原方案均有明显减小,水流平顺,流态有较大改善;出口段流速分布基本均匀。与原方案相比,优化方案上升段和驼峰段流道线型光滑平顺,流速分布较为均匀,下降段虽仍有稍许回流、漩涡现象,但有所缓解,出口段高流速集中在靠近管壁上方位置,流速均匀度有所提高。总体而言,各优化方案较原方案流速分布有明显提高。
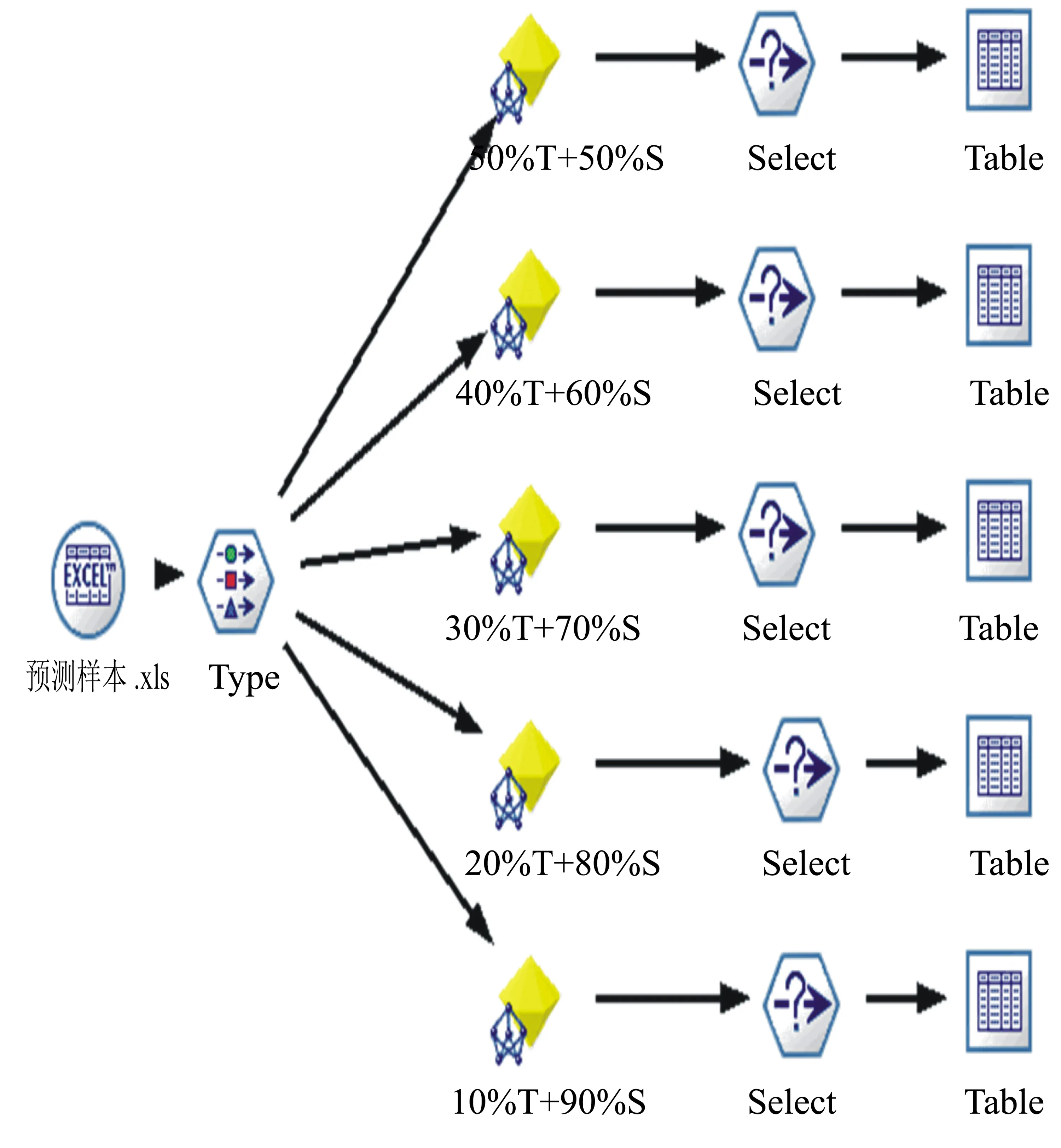
图7 优化样本数据流程设计图

图8 各虹吸管优化方案剖面流速分布图
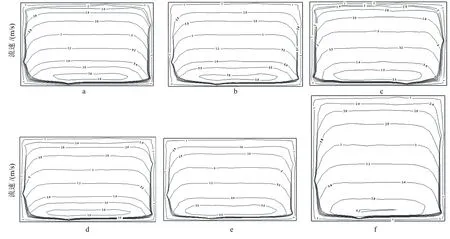
图9 各虹吸管优化方案驼峰断面等值线图

图10 各虹吸管优化方案出口断面等值线图
如图11所示,各优化方案虹吸形成时间较原型的虹吸形成有所增长,但涨幅不大,而水力损失则有较大幅度的降低。在神经网络模型的建立中,水力损失的优化比重设置均大于虹吸形成时间,而这两目标函数在某些设计参数的影响方向上是相异的,这样就导致了最优解的解集结果为水力损失有较大减小,但虹吸形成时间略有增长。可观察到无论是虹吸形成时间还是水力损失,预测数据均小于实测数据,虽两者差值不均,但趋势较为相近。
4 结论
原方案中下降段出现的脱流、回流等现象与出口断面流速分布不均现象在各优化方案中都有很大改善,从而各优化方案水力损失较原方案也有所减小,虽虹吸形成时间略有增长,但总体而言各优化方案对虹吸式出水管水力特性均有改善,证明了利用神经网络算法优化体型这一方法路径是行之有效的。
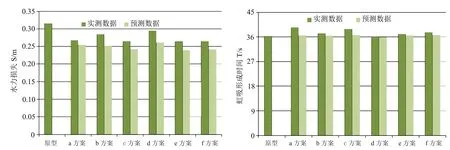
图11 各虹吸管优化方案量化对比图
[1] 于永海,徐辉,陈毓陵,等.城市排污泵站虹吸式出水管水力瞬变过程现场试验分析[J].给水排水,2005,31(9):86-87,88.
[2] 戴红霞.驼峰后带长直管的泵站虹吸式出水流道水力特性研究[D].南京:河海大学,2006.
[3] 冯建刚.城市排水泵站虹吸式出水管水力特性研究[D].南京:河海大学,2010.
[4] 习和忠,王常生,陈秀玉.虹吸式输水管道驼峰断面上压强分布的计算[J].水运工程,1987(7):8-12.
[5] 姜俊红,戴红霞.驼峰后带长直管虹吸式出水流道的水力特性试验研究[J].中国农村水利水电,2008(8):130-132.
[6] 徐辉,史旻.浅论数据挖掘技术及其应用[J].计算机光盘软件与应用,2012(5):119.
[7] 林耀斌,杜友福.基于Clementine神经网络的商品促销效果预测模型应用[J].电脑知识与技术,2009,5(34):9790-9792.
[8] 张帆.基于Clementine的广告客户数据挖掘模型设计与实现[D].北京:北京邮电大学,2010.
(责任编辑:曾小军)
StudyonOptimumDesignofSiphonicOutletPipeShape
TAN Lin-lu1, SUN Yang2
(1. Jiangxi Academy of Hydraulic Science, Nanchang 330029, China;2. Jiangxi Water Conservancy Vocational Institute, Nanchang 330013, China)
On the basis of numerical simulation, we studied the optimum design of siphonic outlet pipe shape by using the neural network algorithm, and obtained the optimal solution set between the parameters and the optimized target. In comparison with adopting the original scheme, adopting the optimized solution-set scheme obviously improved the siphonic performance and interior flow type of outlet pipe. This study can provide reference for the design of siphonic outlet pipe.
Siphonic outlet pipe; Neural network; Numerical simulation; Hydraulic optimized design
TV675
A
1001-8581(2017)12-0102-05
2017-07-10
国家自然科学基金资助项目(51009051);上海市力学在能源工程中的应用重点实验室开放基金。
谭淋露(1988─),女,江西高安人,硕士,主要从事农业水土工程研究。

