热工参数软测量技术在火电厂节能中的应用

贺 军

（贵州兴义电力发展有限公司，贵州 兴义 562400）

热工参数软测量技术在火电厂节能中的应用

贺 军

（贵州兴义电力发展有限公司，贵州 兴义 562400）

本文研究了热工参数软测量技术在火电厂节能中的应用，选取了烟气含氧量和飞灰含碳量两个对机组经济性能有重要影响的指标进行建模，得到了烟气含氧量和飞灰含碳量的软测量模型。为了验证模型的准确性，分别对两个模型的软测量值和实际值进行了比较验证，并采用均方根误差系数RMSE作为衡量指标进行了分析，两个模型的软测量模型输出结果和校验样本的均方根误差分别为0.043和0.039。

火力发电；软测量；支持向量机；烟气含氧量；飞灰含碳量

随着经济的不断发展，节能降耗越来越受到各个行业重视。然而，作为能源消耗大户的电力行业，在节能技术开发和节能效果提升上还有很大的潜力。对燃煤电厂来讲，调整炉膛结构、优化燃烧和运行方式等手段可以提高电厂的经济性，但是我们却忽略了一些关键技术参数测量不准确或者不及时对机组经济性的影响。

例如烟气含氧量、飞灰含碳量以及球磨机负荷等参数，其变化会对电厂的发电效率产生很大的影响，而在实际中，这些参数在技术上或者在成本上的因素往往不能及时准确地被测量到，运行人员不能及时针对上述参数对机组运行进行调整，也就不能使机组取得最大的经济效益。

锅炉烟气含氧量对调整风煤配比具有重要的意义，过高的含氧量会增大排烟损失，过低的含氧量会导致不完全燃烧损失增大。目前，大部分电厂用氧化锆来测量烟气含氧量，该方法需要经常对设备进行维护，耗费大量的人力和物力。飞灰含碳量能够很好的表征锅炉的燃烧效率，但是该参数很难通过直接测量得到，电厂中常见的方法是采用离线分析的方法，因此具有很大的滞后性，不能及时得到锅炉的燃烧情况。针对以上两种对机组性能有重要影响但是又不容易通过测量直接得到的参数，本文提出了软测量的方法，通过对烟气含氧量和飞灰含碳量建立软测量模型，从而实现上述参数的事实测量，进而实现机组的节能。

1 软测量方法简介

软测量方法是一种依靠间接手段对难测量以及不可测量量的估算方法，软测量的关键步骤是找到与被测量关系密切的易于测量的辅助量并建立相应的数学模型。

图1软测量方法示意图给出了建立软测量模型的具体步骤，首先通过对过程对象中系统干扰d和控制变量 u的分析得到辅助变量 x，然后通过软测量模型，以辅助变量 x为输入数据，得到输出变 y的最优解zy。

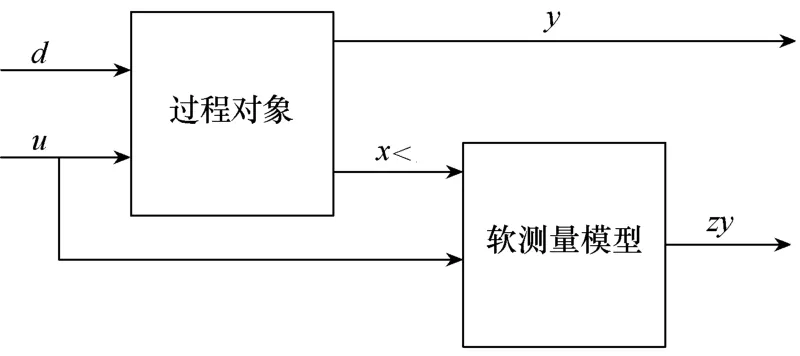
图1 软测量方法示意图

为了保证模型的精度，必须要保证辅助变量 x的准确性，为此需要对现场测量得到的数据进行预处理，去掉一些误差较大的数据，进而保证辅助变量的精确。

2 支持向量机的软测量建模

支持向量机的软测量建模方法是目前较为常用的建模方法。支持向量的基本原理就是通过寻找函数子集中使得经验风险的估值达到最小时的函数，此函数即为最佳的方案。

2.1 支持向量积计算方法

支持向量机计算方法中需要求解得到最优分类面，通过最优分类面来确定分类线，并将不同的类别区分开来。当区分误差为0时所得到的直线为最优分类线，如式（1）。

通过归一化的方法得到样本的集合（xi, yi），i=1, …, n，x∈Rd，y∈{-1，+1}，二者的关系可以用式（2）表示。

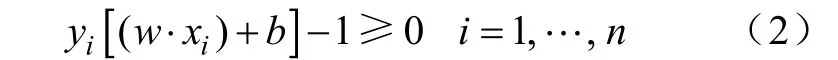
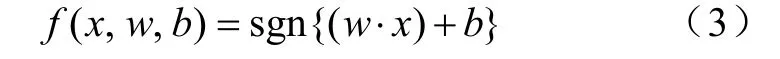
VC维的边界为

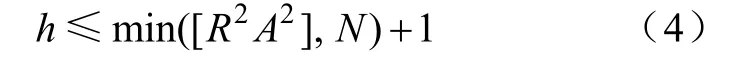
应用支持向量机的方法可以实现对回归问题的求解，首先对样本的集合（xi, yi），i=1, …, n，x∈Rd，y∈R设置回归函数如式（5）：

径向基函数作为核函数，即

最终得到方程为

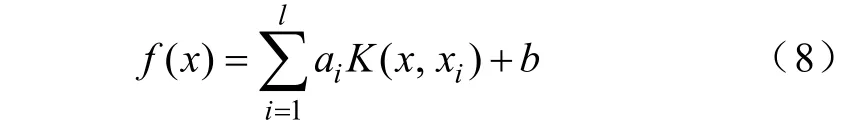
式中，iα和b为未知量，通过对样本数据结合中的数据训练得到。

2.2 模型的建立

烟气含氧量和飞灰含碳量是影响燃煤电厂经济性的主要指标，为此本文主要建立烟气含氧量和飞灰含碳量的软测量模型。

软测量建模主要原则如下：

1）对影响烟气含氧量和飞灰含碳量的原始数据进行采集和处理。采集的数据中不免有一些粗大误差的数据，需要仔细筛选并去除掉这些数据。同时不同辅助变量间的数量级会有较大差异，需要进行归一化处理。

2）对辅助变量进行优化选择。辅助变量是模型的基础数据，模型建立时对辅助变量的要求有两方面：①对所求参数的影响要大；②不同辅助变量之间要有较好的相关性。通过这两条准则可以实现对辅助变量的进一步筛选。

软测量建模流程图如图2所示。

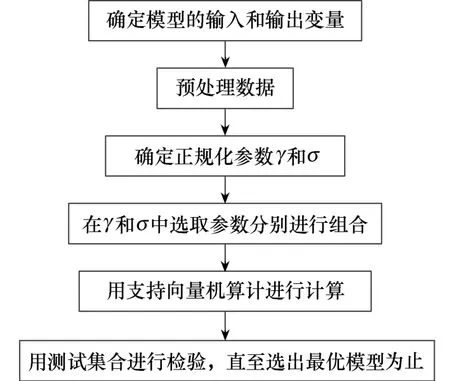
图2 软测量建模流程图

本文选取的模型为某燃煤电厂 600MW 超临界机组，锅炉的燃烧方式为四角切圆燃烧。本文对锅炉烟气含氧量和飞灰含碳量分别建立了软测量模型，其结构如图3和图4所示。

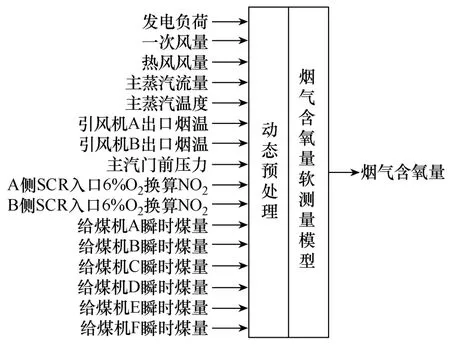
图3 烟气含氧量软测量模型结构

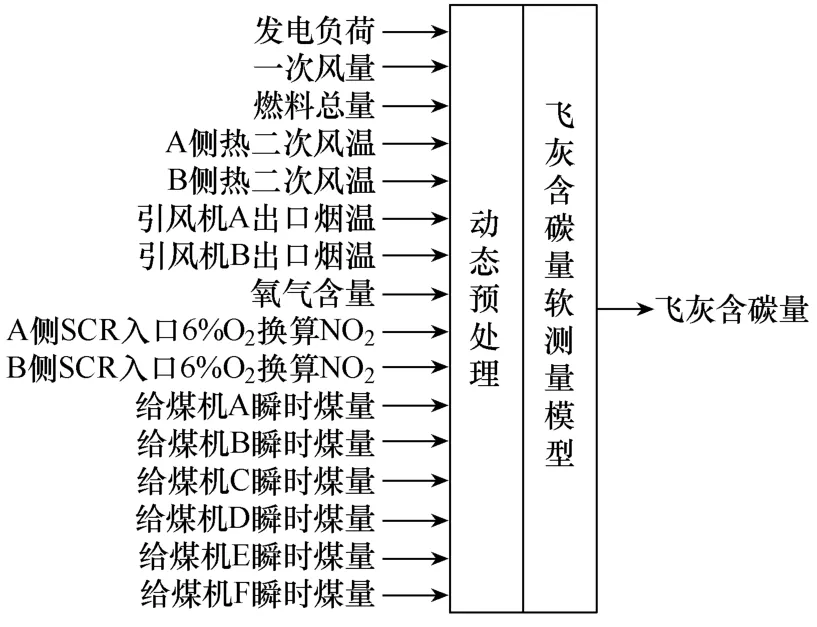
图4 飞灰含碳量软测量模型结构

3 模型验证

为了验证模型的准确性，本文选取电厂100组连续运行数据，通过对其中50组数据进行训练得到烟气含氧量和飞灰含碳量的软测量模型参数，30组用于模型的验证模型的准确性。通过计算得到烟气含氧量支持向量机软测量计算模型的核参数σ=2.0，γ=50，模型的预测值和实际值的比较曲线如图5所示。飞灰含碳量的支持向量机软测量计算模型的核参数σ=2.5，γ=45，模型的预测值和实际值的比较曲线如图6所示。

从图中可以看出，烟气含氧量和飞灰含碳量软测量值和实际值具有很好的吻合性。

为了比较预测值和实际值的偏差，采用均方根误差系数RMSE作为衡量指标。

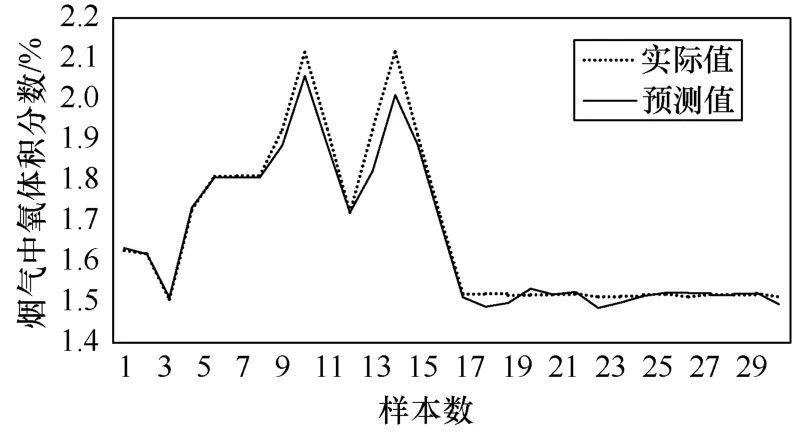
图5 烟气含氧量软测量模型预测值与实际值的比较

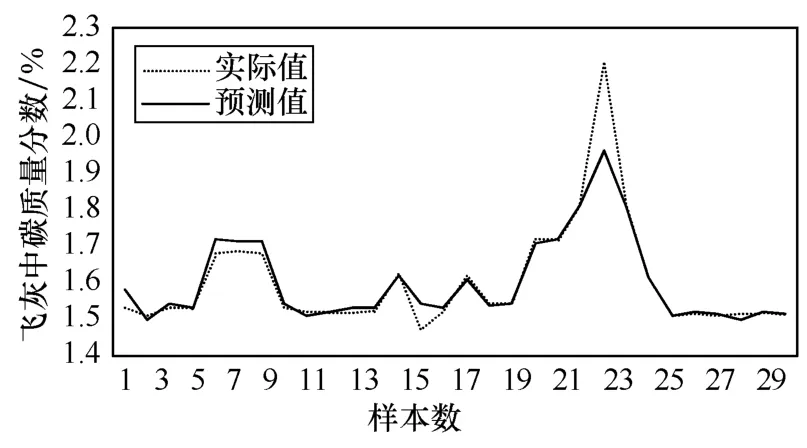
图6 飞灰含碳量软测量模型预测值与实际值的比较

通过计算可以得到烟气含氧量支持向量机软测量模型输出结果和校验样本的均方根误差为0.043，飞灰含碳量支持向量机软测量模型输出结果和校验样本的均方根误差为0.039。由此可见，支持向量机的软测量模型具有较高的精度，可以在实际中应用。

4 结论

1）本文主要研究了支持向量机计算的软测量方法在电厂节能中的应用，选取了烟气含氧量和飞灰含碳量两个对机组经济性能有重要影响的指标进行建模，得到了烟气含氧量和飞灰含碳量的软测量模型。

2）通过烟气含氧量和飞灰含碳量软测量值和实际值的比较验证了模型的有效性。

3）采用均方根误差系数RMSE作为衡量指标，求得烟气含氧量支持向量机软测量模型输出结果和校验样本的均方根误差为0.043，飞灰含碳量支持向量机软测量模型输出结果和校验样本的均方根误差为0.039。

[1] 阎威武, 朱宏栋, 邵惠鹤. 基于最小二乘支持向量机的软测量建模[J]. 系统仿真学报, 2003, 15(10):1494-1496.

[2] 周昊, 朱洪波, 曾庭华, 等. 基于人工神经网络的大型电厂锅炉飞灰含碳量建模[J]. 中国电机工程学报,2002, 22(6): 96-100.

[3] 王剑东, 王东风, 韩璞. 软测量技术及其在电厂热工过程中的应用[J]. 电站系统工程, 2002, 18(5):49-51.

[4] 乔弘. 火电厂热工参数软测量关键技术和方法研究[D]. 北京: 华北电力大学, 2009.

[5] 刘福国, 郝卫东, 韩小岗, 等. 基于烟气成分分析的电站锅炉入炉煤质监测模型[J]. 燃烧科学与技术,2002, 8(5): 441-445.

[6] 方湘涛, 叶念渝. 基于BP神经网络的电厂锅炉飞灰含碳量预测[J]. 华中科技大学学报(自然科学版),2003, 31(12): 75-77.

[7] 刘长良, 孙晓娇, 刘站营. 支持向量机在锅炉飞灰含碳量软测量中的应用[J]. 电力科学与工程, 2010,26(1): 39-43, 59.

[8] 付旭, 丁建设, 潘军民, 等. 基于模型预测控制的火电厂主蒸汽温度优化[J]. 电气技术, 2014, 15(1):126-127.

[9] 郭建仙, 杨帆. ECMS系统在百万机组的应用分析[J].电气技术, 2015, 16(9): 78-82.

The Application of Soft Measurement Technology of Thermal Parameter to Energy Saving in Thermal Power Plant

He Jun
(Xingyi Guizhou Electric Power Development Co., Ltd, Xingyi, Guizhou 562400)

The thermal parameter soft measurement technology in energy saving of thermal power plant has been studied. Two indexes which content on the economic performance of the unit are modeled as oxygen content and the carbon content of fly ash. The soft measurement and actual values of the two models are verified. At the same time, the mean square error coefficient is used as the measurement index. The results of the two models are 0.043 and 0.039 respectively.

thermal power generation; soft measurement; least square support machine; flue gas oxygen content; unburned carbon

贺 军（1979-），男，本科，工程师，从事热工自动控制工作。