Voronoi图在无人机航空影像匹配中的应用

王海涛,张 丹,张 娜

(1. 中国地质大学(武汉)国家地理信息系统工程技术研究中心，湖北 武汉 430074； 2. 湖北省基础地理信息中心(湖北省北斗卫星导航应用技术研究院)，湖北 武汉 430074)

Voronoi图在无人机航空影像匹配中的应用

王海涛1,2,张 丹2,张 娜2

(1. 中国地质大学(武汉)国家地理信息系统工程技术研究中心，湖北 武汉 430074； 2. 湖北省基础地理信息中心(湖北省北斗卫星导航应用技术研究院)，湖北 武汉 430074)

提出了顾及无人机航空影像地面覆盖范围的影像空间位置Voronoi图的生成方法，利用基于局部特征不变算子在多视影像匹配过程的可传递特性，使用影像的Voronoi图邻域关系开展多视影像的匹配，既保证了多视影像间匹配点的重叠度，又提高了多视影像间的匹配速度。

无人机航空摄影；多视影像匹配；Voronoi图

无人机航空摄影是快速获取地理空间数据的一种重要手段[1]，多使用导航型GNSS技术携带小面幅数码相机对地观测，获取的影像数量也较多。无人机航空摄影后处理的首要工作是影像间同名点匹配，考虑影像关系计算的可靠性[2-3]，需要在多视影像间匹配具有多度重叠的同名点。随着无人机航空摄影的广泛应用，对其后处理的实时性要求越来越高，多视影像间同名点的快速匹配需要考虑两个方面：①两幅影像间的快速匹配；②多视影像间匹配策略的优化。

对于两幅影像间的匹配，从无人机航空影像的特点来看，匹配算法要适应：①影像旋转；②仿射变形；③尺度差异；④色彩差异；⑤投影变形等。该方面的算法在David Lowe提出的SIFT(scale-invariant feature transform)[4]算法的基础上不断改进，形成了基于局部特征不变算子[4-12]算法来处理影像间不同形变的匹配。两幅影像间基于特征匹配的速度优可从：①特征描述改进[13]；②特征降维[8-9]；③匹配搜索策略优化[14]；④特征内在关系分析[15-16]等方面来实现。

基于局部特征不变算子影像匹配首先是特征点提取，这样同名点就包含在已知的特征点集内，因此多视影像间匹配同名点是在已知特征点集内开展的，那么已知特征点集内的同名点匹配过程有何特性呢？经分析，多视影像间特征点集内的同名点匹配具有“可传递性”，这样可通过建立多视影像间的邻域关系来提高匹配速度。无人机航空摄影同时获取影像中心点位置信息，可以利用这一信息建立多视影像的邻域关系，Voronoi图是按照最邻近原则对目标的一种空间剖分[17-19]，被广泛应用于几何信息的相关领域[20-22]。本文使用影像空间位置信息生成影像间Voronoi图，并以此构建多视影像的邻域关系，利用特征点集内同名点匹配具有可传递的特性来提高多视影像间的匹配速度。

1 多视影像间匹配分析

从无人机影像变形来考虑，匹配算法要适应影像间的仿射变形、色彩差异等，SIFT[4]算法是一种有效的算法，该算法首先提取特征点，通过统计特征点的梯度直方图来确定特征点主方向，并以主方向对特征点生成128维矢量特征(如图1所示)。从影像关系计算的可靠性来考虑[2-3]，需要在多视影像间匹配多度重叠的同名点，即每张影像与邻域内有重叠的影像进行匹配(如图2所示)，随着影像的重叠度的增大，每张影像与其有重叠的影像数量也在增多，后处理的计算量也大大增加。

图1 SIFT算法特征提取与描述

图2 无人机多视影像重叠关系(随着影像间重叠的增大，每张影像需要匹配的邻域影像也在增多)

基于局部特征不变算子的影像匹配首先是特征提取，这样同名点就包含在已知的特征点集内，因此多视影像间匹配同名点是在已知特征点集内开展，那么特征点集内的同名点匹配过程有何特性，下面以具体实例来分析，如图3所示，地面点P在影像3615、3614、3562、3561上成像点为Pi(i=1～4)，如影像3615上的点P1与影像3614上的点P2匹配成功，影像3614上的点P2与影像3562上的点P3匹配成功，这样影像3615与影像3562不需要匹配，影像3615上的点P1即可传递到影像3562上的点P3，此时点P已有3度重叠，点P的匹配还可以在影像3615的其他邻域影像(如影像3561)间传递。

2 Voronoi图与多视影像匹配

无人机航空摄影同时获取影像中心点坐标，影像间具有明确的空间关系，可借助影像的空间位置关系及特征点集匹配的“可传递性”实现多视影像间的快速匹配。Voronoi图是按照最邻近原则对目标的一种空间剖分[18-19]，已被广泛应用于几何信息的相关领域[20-22]，在此利用影像空间位置生成的Voronoi图来实现多视影像匹配的优化调度。

图3 无人机多视觉影像匹配分析

图4(a)所示为使用某区域无人机航空影像中心点坐标生成的Voronoi图，借助Voronoi图可给出每张影(如影像E)与其他影像的邻域关系，即有公共边的影像作为其邻域影像，这样借助特征点匹配的可传递性，多视影像间匹配仅需要每张影像与其Voronoi图领域影像匹配即可实现快速匹配。

直接使用影像中心点坐标生成影像的Voronoi图存在一些问题，如图4(a)所示，影像A与影像B间没有重叠，但是具有公共边，这样B也被列入影像A的邻域影像，同样影像C和影像D也存在同样问题。需要对Voronoi图生成算法加以改进，本文采用增加辅助点的方式来实现，方法如下(如图4(b)所示)：

(1) 辅助候选点计算：以影像中心点坐标建立辅助正方形，辅助正方形的四个角点作为辅助的候选点。

(2) 辅助点选取：对每张影像的4个候选点，判别是否在其他影像辅助正方形的覆盖范围内，如不在选取为辅助点。

图4(c)所示为使用增加辅助点生成的影像领域关系的Voronoi图，这样计算影像邻域关系更加合理。

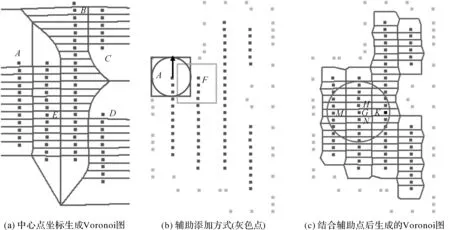
图4 无人机航空影像Voronoi图生成

3 多视影像间匹配工作的开展

3.1 多视影像匹配流程

由第1节分析可知，使用SIFT特征点集在多视影像间匹配，同名点匹配具有“可传递性”，利用这一特性并结合影像间的Voronoi图关系可以提高多视影像间匹配速度，如图4(c)所示，影像G仅需要与影像H、K、M、N匹配即可，不需要与其有重叠度的所有影像(图4(c)圆圈范围内的影像)匹配。

如图4(c)所示，影像G的邻域包括影像H，影像H的邻域包括影像G，这样影像G与影像H仅需要匹配一次，当影像G与影像H匹配完成后将匹配结果保存，当影像H与影像G匹配时，直接使用已记录的结果即可。考虑利用多核并行计算的开展，在影像匹配前建立影像关系表(以影像G、H为例，当影像G的关系中有影像H时，影像H的关系表中不需要包含影像G)。由本节分析可知，利用影像Voronoi图关系开展多视影像匹配，考虑影像匹配的双向性及多核心并行计算的开展，本文的影像匹配流程如图5所示。

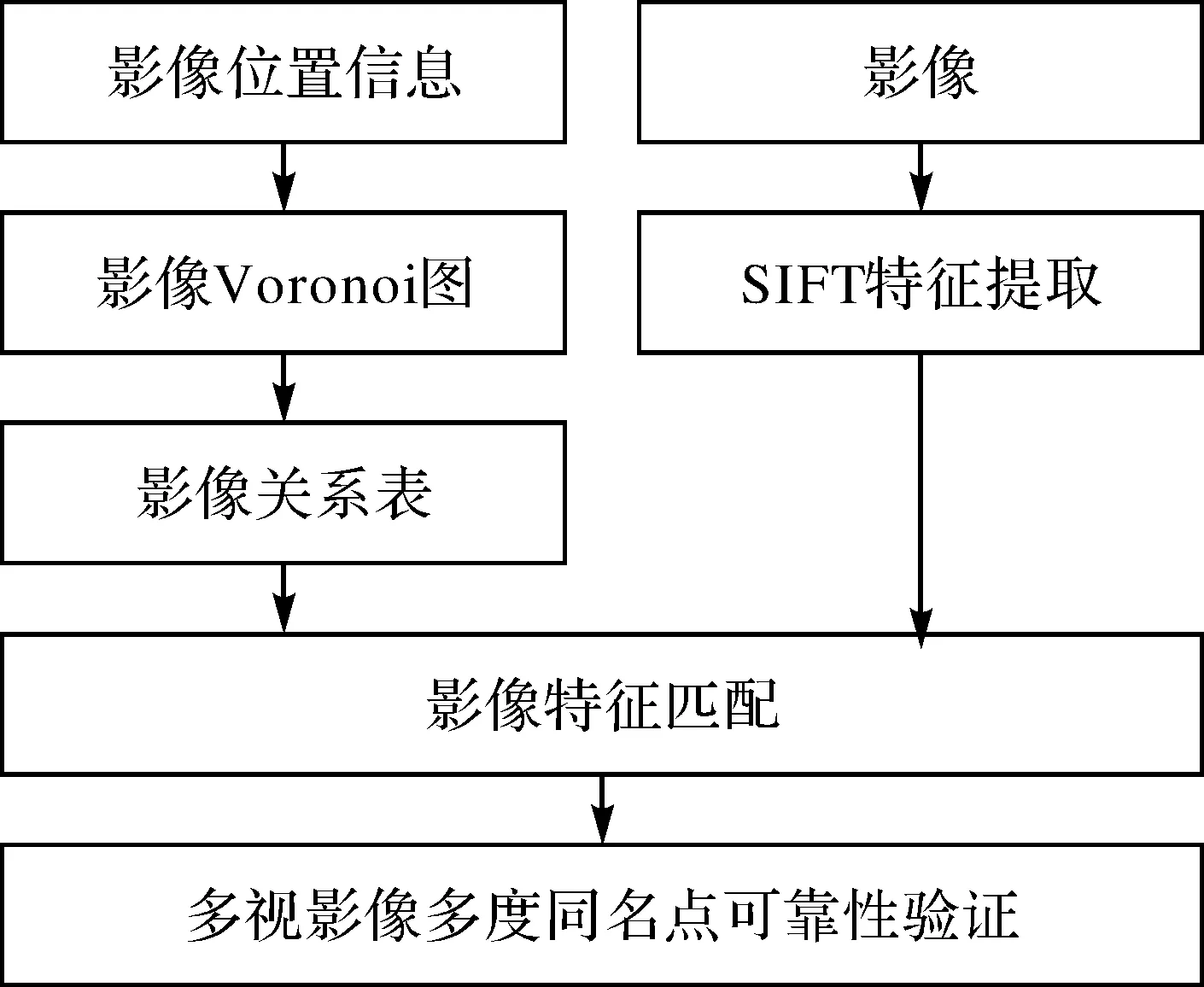
图5 多视影像匹配流程

3.2 多视影间匹配的可靠性处理

设影像特征点的SIFT描述子(归一化的128位描述子)为H=(h1,h2,…,h128)，则两幅影像间点i、j的相似度可采用欧氏距离来计算

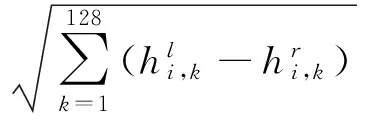
(1)

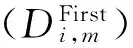
(2)

除采用距离比值方法量判断特征点之外，本文还采用核线约束[17]、双向一致性、匹配唯一性原则来提高匹配的可靠性，具体要求见表1。

表1 点匹配策略表及要求

图6中，Ai、Bj为左右影像特征点，如点A1与B1满足双向一致性要求，但如点A3对应目标点B4，B4对应目标点A4，不满足双向一致性要求。图7中，Ai、Bj为左右影像特征点，如点A1仅有一个同名点B1满足唯一性要求；如点A3对应两个目标点B4、B5，因此A3不满足唯一性要求。

对于核线约束，采用同名点计算本征矩阵F的方式实现，设左右影像同名点Al、Ar的坐标为xl、xr，则xlFxr=0，通过已知点同名点计算F并剔除错误点。

多视影像在匹配的“传递”过程中仍然有错误存在，SIFT点描述子H，对其相似度可采用欧氏距离，也可使用相关系数计算(式3)，对多视影像匹配的多度同名点计算相关系数进一步加以验证(在此取C≥0.85)。

(3)

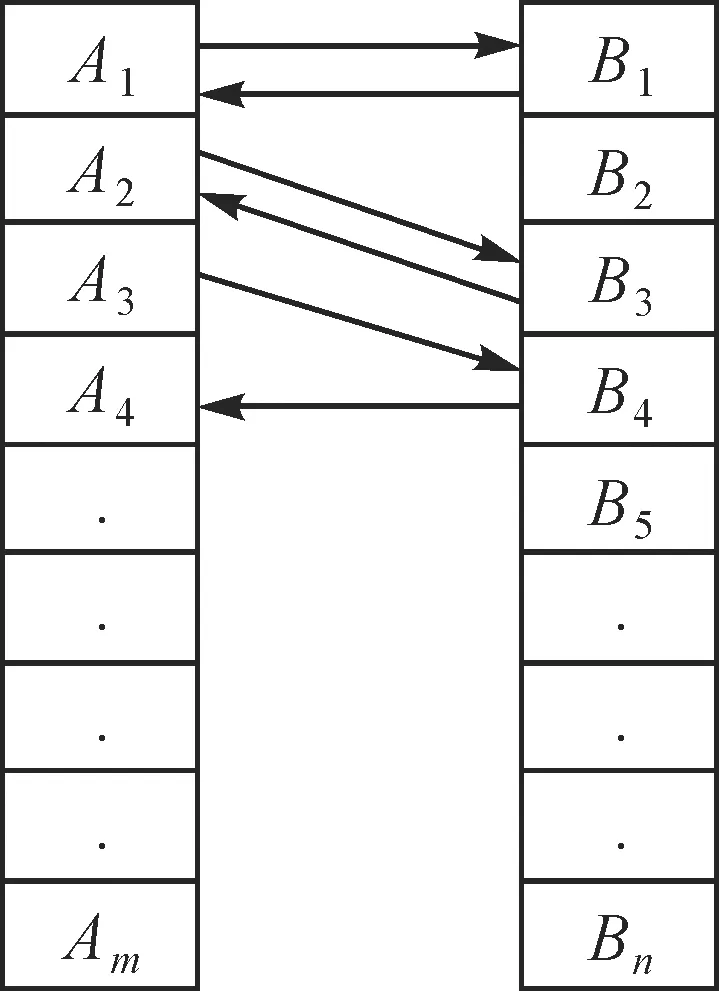
图6 匹配双向一致性

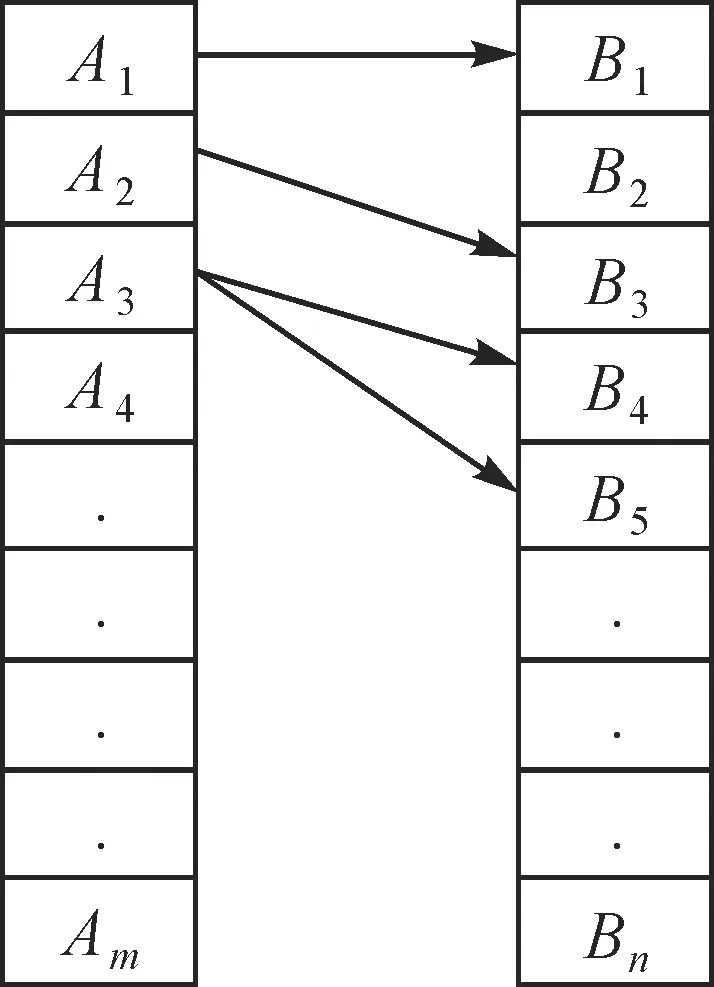
图7 匹配唯一性

4 试验分析

传统多视影像匹配是对每张影像在一定半径内搜索与其有重叠的影像匹配(在此称为半径搜索匹配，简称R-匹配)，本文利用影像Voronoi图邻域方式开展多视影像匹配(在此称为V图邻域匹配，简称V-匹配)。

从多视影像匹配的可靠性要求来考虑，R-匹配可有效保证影像点匹配的多度重叠，针对V-匹配是否可保证影像点匹配的多度重叠的问题，本文选取3组样例数据(见表2)来验证匹配效率和特征点的重叠度，结果如图8和表3所示。试验表明，R-匹配与V-匹配同名点的重叠度相当，但是后者可以大幅度提高匹配速度，匹配效率的加速比与影像的重叠度有关，加速比随着影像间的重叠度增大而增大。

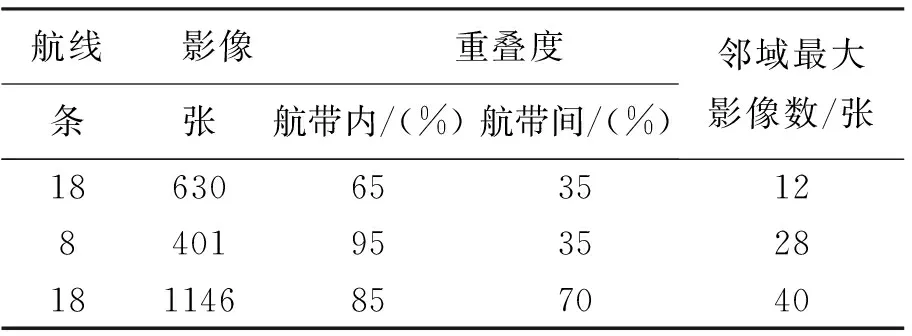
表2 样例影像数据信息

图8 匹配点重叠度分析

匹配时间/sR-匹配V-匹配加速比220278.152701419.2320907727.14

5 结 论

从无人机航空影像的特点来看，匹配算法要适应：①影像旋转；②仿射变形；③尺度差异；④色彩差异；⑤投影变形；⑥视点变化等。基于局部特征不变算子的影像匹配是一种有效的方法，该方法提取的特征点在多视影像间的同名点匹配过程具有“可传递性”，利用这一特性，使用影像空间位置信息生产顾及影像覆盖范围的Voronoi图，并构建了影像的邻域关系，这样构建的影像邻域关系更加合理，然后利用影像Voronoi图邻域关系开展多视影像间匹配，既保证了匹配同名点重叠度，又提高了多视影像间的匹配效率。

[1] 李德仁,李明. 无人机遥感系统的研究进展与应用前景[J]. 武汉大学学报(信息科学版), 2014, 39(5): 505-513.

[2] 李德仁,袁修孝.误差处理与可靠性理论[M].2版.武汉：武汉大学出版社,2012.

[3] HARTLEY R, ZISSERMAN A. Multiple View Geometry in Computer Vision[M].Cambridge: Cambridge University Press,2004.

[4] LOWE D G. Distinctive Image Features from Scale-Invariant Keypoints[J].Internation Journal of Computer Vision,2004,60(2):91-110.

[5] HERBERT Bay, ANDREAS Ess, TINNE Tuytelaars, et al. SURF: Speeded Up Robust Features[J]. Computer Vision and Image Understanding, 2006,110(3): 404-417.

[6] YAN K, SUKTHANKAR R. PCA-SIFT:A More Distinctive Representation for Local Image Descriptors[J].IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2004,2(2): 506-513.

[7] MIKOLAJCZYK K, SCHMID C. A Performance Evaluation of Local Descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10):1615-1630.

[8] WANG Zhenhua, FAN Bin, WU Fuchao. Local Intensity Order Pattern for Feature Description[J]. International Conference on Computer Vision, 2011,23(5):603-610.

[9] ABDELHAKIM A E, FARAG A A. CSIFT: A SIFT Descriptor with Color Invariant Characteristics[C]∥2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2006). New York, NY, USA: IEEE, 2006.

[10] MIKOLAJCZYK K, TUYTELAARS T, SCHMID C, et al. A Comparison of Affine Region Detectors[J]. International Journal of Computer Vision,2005,65(1-2): 43-72.

[11] MIKOLAJCZYK K, SCHMID C. Scale & Affine Invariant Interest Point Detectors[J]. International Journal of Computer Vision,2004,60(1):63-86.

[12] MOREL J M, YU G, ASIFT: A New Framework for Fully Affine Invariant Image Comparison[J]. SIAM Journal on Imaging Sciences, 2010, 2(2)：438-469.

[13] OJALA T, PIETIKINEN M, MAENPT. Multiresolution Gray-scale and Rotation Invariant Texture Classification with Local Binary Patterns[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(7):971-987.

[14] MIKOLAJCZY K, MATAS J G. Improving Descriptors for Fast Tree Matching by Optimal Linear Projection[C]∥IEEE International Conference on Computer Vision. [S.l.]: IEEE, 2007.

[15] GRABNER M, GRABNER H, BISCHOF H. Fast Appro-ximated SIFT[C]∥Asian Conference on Computer Vision. Hyderabad, India:[s.n.], 2006: 918-927.

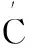
[17] HAN J H,PARK J S. Contour Matching Using Epipolar Geometry[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2000,22(4):358-370.

[18] AURENHAMMER F. Voronoi Diagram: A Survey of a Fundamental Geometric Data Structure[J]. ACM Computing Surveys,1991,23(3):345-405.

[19] GOLD C M. The Meaning of ‘Neighbour’[C]. Lecture Notes in Computing Science. Berlin:Springer-verlag,1992: 200-235.

[20] 潘俊，王密，李德仁. 基于顾及重叠的面Voronoi图的接缝线网络生成方法[J]. 武汉大学学报(信息科学版), 2009, 34(5): 518-521.

[21] 乔朝飞，赵仁亮，陈军,等. 基于Voronoi内邻近的等高线树生成法 [J]. 武汉大学学报(信息科学版), 2005, 30(9): 801-804.

[22] 李佳田,康顺,李晓娟,等. 宽泛地理注记的投放模型[J]. 武汉大学学报(信息科学版), 2015, 40(1): 20-25.

ApplicationofVoronoiDiagraminUAVAerialImageMatching

WANG Haitao1,2,ZHANG Dan2,ZHANG Na2

(1. National Engineering Research Center for Geographic Information System, Wuhan 430074, China; 2. Hubei Geomatics Information Center(Hubei Institute of BeiDou Satellite Navigation Applied Technology)， Wuhan 430074,China)

A method of generating Voronoi diagram of the spatial location of UAV aerial images is presented in this paper. This method takes the ground coverage of images into account. A matching algorithm based on local invariant features, which is transferable during the matching procedure between multi-view images, combined with Voronoi diagram of images is used to improve the matching speed and the degree of overlapping of corresponding points between multi-view images.

UAV aerial photography;multView image matching;voronoi diagram

王海涛,张丹,张娜.Voronoi图在无人机航空影像匹配中的应用[J].测绘通报，2017(11)：118-122.

10.13474/j.cnki.11-2246.2017.0360.

P23

A

0494-0911(2017)11-0118-05

2017-08-09

国家高科技研究发展计划863(2013AA122104)；测绘地理信息公益性行业科研专项(201512012)

王海涛(1976—)，男，博士生，高级工程师，主要研究方向为摄影测量与计算机视觉。E-mail:306550757@qq.com