Titanic生存问题常见分类算法对比分析
贵州大学大数据与信息工程学院 郑晓静 朱 桐
Titanic生存问题常见分类算法对比分析
贵州大学大数据与信息工程学院 郑晓静 朱 桐
为了分析Titanic人员生存问题,针对生存与否使用常见的六种二分类模型进行了分析判断,通过对各模型准确率及效率的分析比较,发现SVM算法在解决此问题时的准确率较高,且计算时间较短。
Titanic生存问题;机器学习;分类算法
引言
泰坦尼克号沉没事故为和平时期死伤人数最惨重的海难之一,在2224名船员及乘客中,逾1500人丧生。 而决定船上人员存活状况的条件也由多种因素决定着,此文通过k-近邻分类算法,逻辑回归,支持向量机,朴素贝叶斯,决策树及随机森林共六种算法分别实现对Titanic人员数据的分类判别,研究其准确率及相对效率。
1.问题分析
针对Titanic人员生存判断问题,此处我们使用kaggle平台的Titanic人员生存数据集为样本,通过对船上人员的年龄、性别、座号,船舱等级、亲属关系等信息作为影响因素来使用几种不同的分类算法进行生存状况分析。
2.数据预处理
Titanic人员生存数据共1309组,其中取前891组数据为学习样本,剩余418组数据为测试样本。
为消除数据中各指标之间的量纲和取值范围差异的影响,此处采用离差标准化对原始数据进行线性变换,将数值映射到[0,1]区间,公式如下:
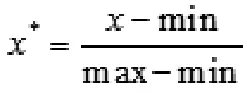
其中max为单维度样本数据最大值,min为单维度样本数据最小值。
3.分类算法
3.1 k-近邻分类算法
kNN算法是一种常用的监督学习方法,通过学习样本的学习后,再用测试样本分类检验,如果测试样本中一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性[1]。从而得出该样本的分类结果,即人员的存活状况。
3.2 Logistic Regression 算法
逻辑回归算法主要是对现有的数据对分类边界线建立回归公式,以此分类。通过使用梯度上升法对学习样本进行计算,求出最佳回归系数ωT,将Sigmoid函数的输入记为z,代入测试样本,设为测试样本Titanic人员信息的n个特征值,在样本每个特征上乘以一个回归系数,然后把所得的值相加,则可求出z为:

将求出的z值代入下列Sigmoid函数中:

则可得到一个范围在[0,1]之间的数值,任何大于0.5的数据判定为1类(生还),小于0.5的判定为0类(死亡)。
3.3 支持向量机
支持向量机是一种二类分类模型,在此将生还状况看成一类,将死亡状况看成一类。
设学习样本集为:

其中yi为输出,把m个样本点看作是n维空间的点,如果存在一个超平面:
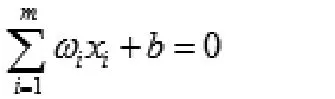
这个超平面能将m个样本分作两类,且使得分类间隔最大即使得最小,则可转化为一个凸二次规划问题的求解则,如下所示:


根据优化理论,可得出以下决策式:

3.4 朴素贝叶斯分类器
朴素贝叶斯分类器是一种应用概率模型贝叶斯定理的简单概率分类器。
通过对学习样本对生还和死亡状况的先验概率进行计算,然后再建立后验概率模型,使用测试样本集分别进行判别分类。
其后验概率公式为:
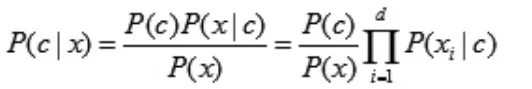
其中d为属性数目,xi为x在第i个属性上的取值。
若一条数据的生还后验概率大于死亡后验概率,则该条数据的人员生还,反之则人员死亡。
3.5 决策树分类器
决策树是一个树结构。其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别[2]。使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。
本文通过ID3算法来对决策树属性进行划分,计算各根节点的信息熵,令Titanic人员生存情况学习样本为C,设第k类样本所占比例为:

则信息熵定义为:

由信息熵大小对决策树属性意义划分,构造出树的数据结构,在将测试数据集带入构造好的决策树分类,得出结果。

表1 六种分类方法正确率及消耗时间
3.6 随机森林
随机森林算法用学习样本数据随机生成N个训练子集,每个子集的生成从原始样本中随机抽取三分之二,抽取后放回继续抽样,避免局部许最优解,决策树节点分裂时,对于M个输入变量,随机抽取指定logM+1个随机特征变量,减少构建的随机森林中决策树之间的相关性[3]。在输入测试样本时,让构建好的随机森林每一棵决策树分别判别,选择多的分类结果即为最终的分类结果。
4.结果比较(见表1)
5.结论
本文列举了共六种处理Titanic人员生存问题的分类方法,通过对六种方法的正确率和效率的分析研究,我们可以看出,支持向量机算法在处理Titanic人员生存问题上更加具备优势,在具备良好正确率的同时,其消耗时间也相对适宜。
[1]周洲.K近邻法在 matlab 上的应用与分析[J].商情,2013(12):159-159.
[2]陈丽芳,王云,张奉.粗决策树动态规则提取算法研究及应用[J].计算机应用,2015,35(11):3222-3226.
[3]曹正凤.随机森林算法优化研究[D].首都经济贸易大学,2014.

