要素投入及结构变动对经济增长稳定性的影响研究
(云南大学 发展研究院,云南 昆明 650091)
要素投入及结构变动对经济增长稳定性的影响研究
赵鑫铖,张利军
(云南大学 发展研究院,云南 昆明 650091)
从供给侧的要素投入和要素结构角度研究了我国经济增长稳定性,对我国经济在“十三五”及未来很长一段时间实现中高速稳定增长具有重要的理论意义和现实意义。依据增长核算理论和时变参数模型,分两个层面分析了要素投入和要素结构变动对经济增长及其稳定性的影响。增长核算角度分析结果表明,劳动投入、资本投入、全要素生产率增长率分别波动1%,将导致经济增长波动0.5046%、0.4954%、1%;基于时变参数模型分析表明:1978—1991年,资本冲击、劳动冲击和要素结构变化冲击较为剧烈,1992年至今,资本冲击是经济稳定性的降低主要原因,劳动冲击对经济稳定性的影响较小,而要素结构冲击缓解了经济波动且提高了经济增长稳定性。
要素投入;要素结构;经济增长;增长核算;时变参数模型
1 引言
要素投入是经济增长最直接的动力,而要素结构通过要素在不同产业、地区间的配置也会对经济增长产生重要影响。在供给侧结构性改革已成为我国“十三五”时期经济政策导向的背景下,从供给侧的要素投入和要素结构角度研究了我国经济增长稳定性,对我国经济在“十三五”及未来很长一段时间实现中高速稳定增长具有重要的理论意义和现实意义。
本文从两个层面分析了要素投入、要素结构对经济增长稳定性的影响:一是沿用传统的增长核算理论,分析了各投入要素对经济增长的贡献,进而探讨了当要素投入发生波动时对经济增长的影响;二是以传统总量生产函数为基础,通过构建状态空间模型分析了劳动冲击、资本冲击及要素结构变动对我国经济增长稳定性的影响。
2 要素投入、要素结构与经济增长稳定性
经济增长理论表明,要素投入和生产技术结合起来形成经济的产出。一般来说,最重要的投入要素分别是资本、劳动力和技术,资本可进一步可划分为人力资本、物质资本和社会资本等。当各要素投入发生波动时,产出也会发生波动,因此要素结构的变动也会影响经济增长的稳定性[1]。基于要素与增长的关系,测算资本、劳动等要素投入的收入份额(即产出的要素弹性),分析我国长期经济增长的要素投入及其结构特征。在此基础上,利用增长核算模型分析要素结构对我国经济增长稳定性的影响。
2.1 增长核算模型
阿布拉莫维茨和索洛共同创立了增长核算理论来解决经济增长的源泉问题[2,3],他们在模型中主要考虑了劳动力投入、资本投入和技术进步对经济增长的推动作用。考虑总量生产函数Y(t)=F[A(t),K(t),L(t)],总产出y(t)对时间t求导数,可得:
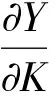
(1)

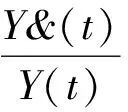
(2)
=αK(t)gK+αL(t)gL+B(t)
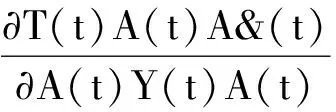
式(2)中的各项分别反映了各因素的增长对产出的贡献:等式左边反映了产出的增长,右边第一、二、三项分别反映了资本、劳动和人力资本对产出的贡献。在关于经济增长因素分析的实证研究中,生产函数的形式一般采用柯布—道格拉斯形式,即:
Y(t)=F[A(t),K(t),L(t)]=A(t)K(t)αL(t)β
(3)
式中,A(t)为t时期的技术水平,假设A(t)=A0eα0t,则Y(t)=A0eα0tK(t)αL(t)β,对该式两边求对数,得:
lnY(t)=lnA0+α0t+αlnK(t)+βlnL(t)
(4)
2.2 我国经济增长的要素投入及其结构特征
数据来源:本文模型分析所需数据包括我国实际的经济产出、资本存量和劳动力等3个指标,对相关指标说明如下:对产出,取GDP作为产出的衡量指标,并用GDP指数折算为1978年不变价;对劳动力,直接采用我国的就业人员数量代表劳动力投入;对资本存量的核算,1978—2015年的数据(1952年的不变价格)来源于单豪杰[5]关于省际资本存量数据的整理,并换算为1978年不变价格。考虑到数据的可得性,本文选取了1978—2015年的有关数据(表1),数据主要来源于《新中国60年统计资料汇编》和2016年的《中国统计年鉴》。
2.3 要素投入结构变化分析
由于其他要素的度量相对比较困难,因此在进行经济增长分析时,我们笼统地将除劳动力和物质资本外的所有要素称为全要素,它对经济增长的贡献由全要素生产率来衡量。
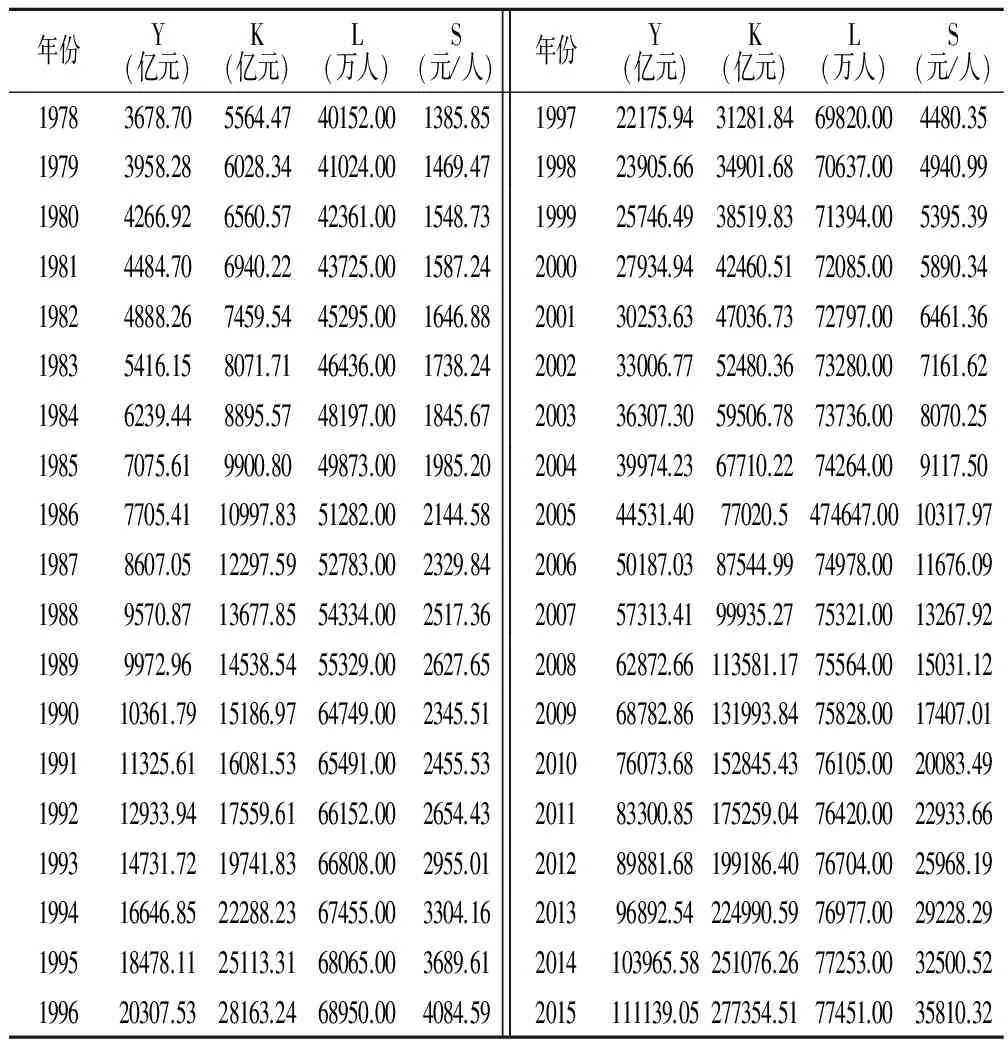
表1 我国1978—2015年相关经济数据
注:数据来源于2015年《中国统计年鉴》和作者的计算;S为资本劳动比,即下文中要素结构的衡量指标。
要素投入结构变动趋势:1978—2015年我国劳动力和物质资本投入的结构变动特征表现为:首先,从资本投入和劳动投入的变化特征来看,1978—2015年我国资本积累的增长速度远远高于劳动力投入的增长速度。具体来看,1978年的资本存量为5564.47亿元(1978年不变价),2015年增长到28163.24亿元,是1978年的49.84倍;而劳动力投入1978年为40152万人,2015年增加到77451万人,是1978年的1.93倍。图1给出了1978—2015年我国的资本劳动比(1978年不变价,元/人)。可以看出,我国的人均资本存量的变化经历了三个阶段:第一阶段(1978—1991年),这一时期我国的人均资本存量基本维持在2500元/人上下波动;第二阶段(1992—2000年),这一时期我国人均资本存量增长速度开始上升;第三阶段(2000—2015年),这一时期我国人均资本存量增长速度急剧上升。
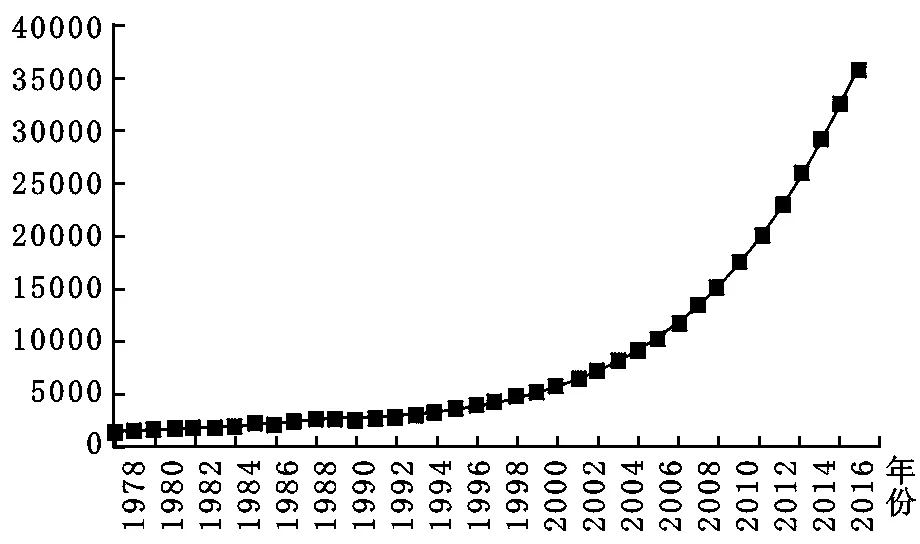
图1 1978—2015年我国的资本劳动比(元/人)
从资本和劳动投入的增长率来看(表2),1978—2015年我国资本投入年平均增长率与经济增长率基本持平,分别为11.14%和9.65%,而劳动投入年均增长率则远低于资本投入,为1.79%。我国要素投入的变化也体现出阶段性的特征:第一个阶段(1978—1991年),资本增长率相对较低,而劳动增长率较高,经济增长主要依靠的是要素投入效率的提高;第二阶段(1992—2000年),资本投入增长率急剧上升到11.67%,而劳动投入增长率由于计划生育政策效果显现而降低为1.08%,经济增长的投资驱动特征开始显现;第三阶段(2000—2015年),资本投入依然维持高增长的13.33%,劳动力投入增长率降低为0.48%。进入第三阶段后,经济增长的资本驱动特性进一步凸显,资本投入的效率也由于投资的持续增加有所下降,如何提高资本和劳动的利用效率进而实现经济增长方式由要素投入驱动向创新驱动转变是我国经济面临的最为严峻的问题。
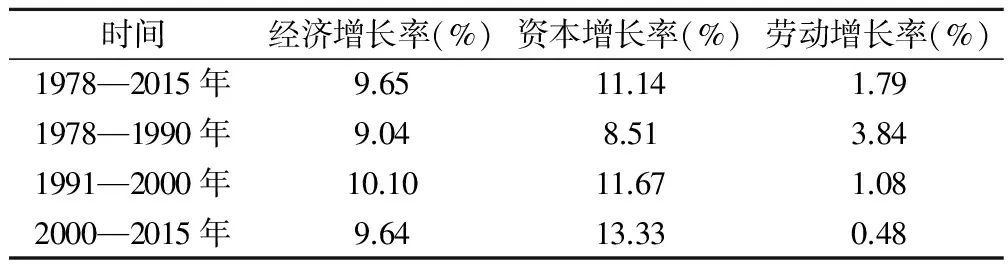
表2 我国不同时期要素投入量的平均增长率
从劳动力供给的角度看,未来十年我国人口自然增长率会有所下降,但由于“单独二胎”、“全面二胎”等政策的实施,我国就业人口将维持年均1.2%水平增长。从资本投入,未来十年我国资本存量的增长速度将会由于经济增长方式转变的实现和结构调整等因素有所回落,考虑到我国的投资驱动特征,资本投入的增长率能维持在10%以上的增长速度。
回归分析:由于本文的数据为时间序列,为避免伪回归的出现,先对数据进行平稳性检验,检验结果表明,产出对数ln(Y)、资本存量对数ln(K)和劳动力对数ln(L)均为1阶单整序列,且协整检验表明三个变量之间存在协整关系,可以进行回归分析(由于篇幅限制,单位根检验和协整检验结果从略)。在回归分析前,运用Wald检验方法对式(4)检验规模报酬不变α+β=1的假设,检验结果见表3。

表3 生产函数规模报酬不变的Wald检验
Wald检验结果表明,Pgt;0.05表明在5%的显著水平上不能拒绝原假设,即我国经济在1978—2015年规模报酬不变。因此,通过将式(4)两边同时减去lnL,得人均形式的增长核算方程:
ln[Y(t)/L(t)]=lnA0+α0t+αln[K(t)/L(t)]
(5)
运用表1的数据对式(5)进行估计,结果如下:
lnY/L=-1.4155+0.0328t+0.4954(K/L)
(-11.3495) (6.754) (9.54)
AR(1)=1.2270 (t统计量为8.090)
AR(2)=-0.630 (t统计量为-4.051)
R2=0.9994,F=1376.49,DW=1.899
(6)
式(6)的估计结果表明,各变量t统计量显著,不存在自相关,模型整体拟合结果较好。资本产出弹性为0.4954,由于生产函数具有规模报酬不变特征,则劳动产出弹性为0.5046,全要素生产率的增长率为0.0328,这一估计结果与赵志耘等[6]、陈彦斌、姚一旻[7]对要素产出弹性估计结果一致。
2.4 要素结构对我国经济增长稳定性的影响
根据实证分析结果式(6),我国各生产要素增长率的波动会直接导致经济增长的波动:劳动投入增长率波动1%,会导致经济增长率波动0.5046%;资本投入增长率波动1%,会导致经济增长率波动0.4954%;全要素生产率增长率波动1%,将导致经济增长波动1%。从各要素自身的波动程度来看,劳动要素由于人口演变规律的制约,其波动性相对较小;而资本要素是通过投资累积而成的,投资往往随经济周期会发生大的波动,因此资本要素的波动性一般较大[8];全要素生产率波动是经济波动的主要来源[9,10]。
3 要素投入与结构变动对经济增长的影响
根据总量生产函数可知,要素投入结合生产技术得到经济的产出,因此要素投入和要素结构变动会导致产出水平的波动。国内学者从要素投入角度研究了要素投入与经济波动(经济稳定)的关系,具有代表性的有:郭庆旺、贾俊雪[11]运用产出缺口、投资缺口和全要素生产率缺口分别度量了产出波动、投资波动和全要素生产率波动,并结合中国经济数据分析了投资冲击和全要素生产率冲击(波动)对经济波动的影响,结果表明,投资冲击和全要素生产率冲击都是我国经济波动的重要原因,但全要素生产率的影响程度更大且持续时间更长。陈亮[12]通过省级面板数据分析了外生冲击、要素投入变化对我国产出波动的影响,分析结果表明投资波动显著加剧了经济波动,而劳动投入的波动并不会加剧经济波动。冉光和、曹跃群、钟德华[13]考察了要素投入、货币供应和技术进步对中国经济波动的影响,指出资本投入波动是中国经济波动的主要原因,货币波动次之,技术进步对经济波动的影响相对较小但更为持久。方福前、詹新宇[14]分析了资本冲击、劳动冲击和产业结构升级对我国经济波动的影响,这种影响呈现出阶段性:以1992年为界,1992年前资本冲击、劳动冲击和产业结构升级的变动都比较剧烈;1992年后资本对经济的冲击最大,而劳动次之,产业结构升级的冲击一直为负。邓可斌等[15]通过结构GMM模型分析了要素投入对经济增长与波动的影响,结果表明要素投入特别是资本投入对经济增长稳定性有重要的影响。本文以传统总量生产函数为基础,通过构建状态空间模型来分析劳动、资本、要素结构变动对我国经济波动(稳定)的影响。
3.1 理论模型
借鉴方福前、詹新宇[12]的模型,将劳动、资本、要素结构、技术等指标一起纳入总量生产函数:
Yt=F(Kt,Lt,St,At)
(7)
式中,Yt为产出水平;Kt为资本投入;Lt为劳动投入;St为要素结构,由于模型中只简单考虑了两种生产要素,用资本劳动比来衡量;At为技术水平(短期中用常数c来表示)。对式(7)两边取对数得线性的生产函数:
lnY=c+αlnK+βlnL+γlnS+μt
(8)
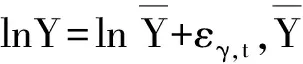
εY,t=c+αεK,t+βεL,t+γεS,t+μt
(9)
式(9)给出了资本波动、劳动波动和要素结构变动是如何影响产出的波动。此外,设Y%=εY,t、K%=εK,t、L%=εL,t、S%=εS,t,从而式(3)变为:
(10)
式(10)即为测度资本波动、劳动波动和要素结构变动对经济波动影响的主要模型。
3.2 状态空间模型
采用1978—2015年我国宏观经济数据进行分析,数据属于时间序列,考虑到改革开放以来我国经济结构、制度环境等发生了较大的变化,若采用传统的固定参数模型将难以捕捉要素结构变化对经济波动的影响,通过计量经济学中的状态空间模型来建立时变参数模型[16]:
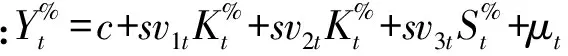
(11)
状态方程:sv1t=γ1sv1t-1+η1t,sv2t=γ2sv2t-1+η2t,sv3t=γ3sv3t-1+η3t
(12)
其中,μt和ηit的均值为0且彼此相互独立,即有
3.3 数据处理与实证分析
基础数据来源:式(8)中产出Y、资本存量K、劳动力L与表2相同,要素结构指标S通过资本存量K除以劳动力获得,基础数据见表1。
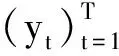
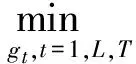
(13)
式中,yt为经济变量的对数值;gt为经济变量的趋势成分;λ为观测者选取的一个参数对于年度数据;λ一般选取100。对经济变量的对数值进行滤波处理后得到经济变量的波动成分Y%,K%、L%和S%(图2)。
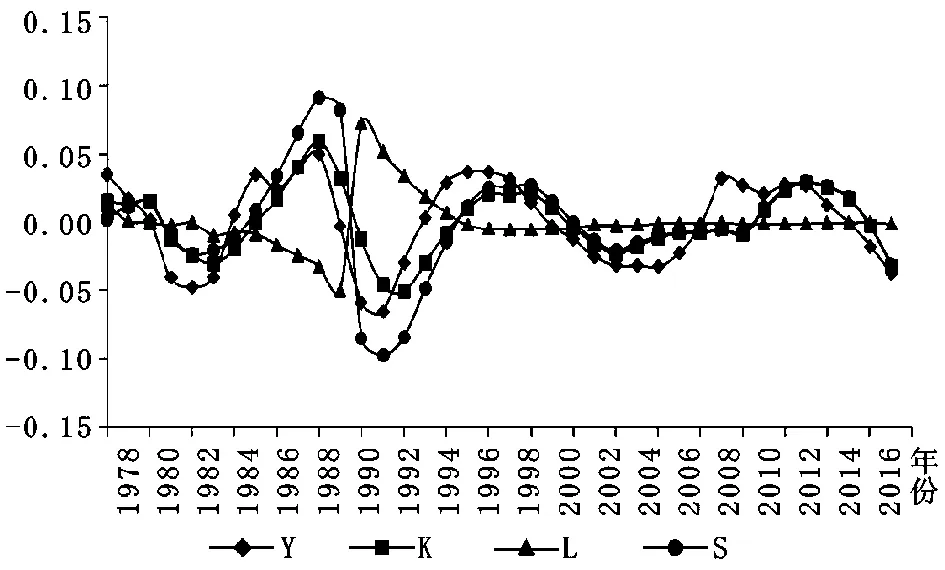
注:从图2反映的特征可见,我国就业人员统计在1989—1990年进行了统计口径的调整,1989年就业人员数为55329万人,1990年为64749万人,就业人员一年时间增加了近1亿人,与此前和此后年平均增加10000多万人形成了鲜明的对比。由于找不到合适调整的方法,本文没有对数据进行调整。
考虑到20世纪90年代是我国市场化改革的转折点,以1992年为界将本节考察的时间序列1978—2015划分为两个阶段:1978—1991年和1992—2015年,经济波动、要素冲击与结构变化特征见表4。总体来看,各要素冲击的波动性在改革开放的第一阶段要高于第二阶段,这主要是由于改革开放前的计划经济体制受社会保障、投资体制等体制改革影响较大,对生产要素产生了比较大的冲击。而从波动幅度来看,第一阶段(1978—1991年),要素结构变化最大,经济波动次之,资本冲击和要素冲击基本相当;第二阶段(1992—2015年),经济波动、各要素及结构的波动幅度较第一阶段都有不同程度的下降,要素结构变化最大,经济波动和资本冲击次之,劳动冲击最小。从各要素及结构的周期性来看,资本和要素结构呈现出顺周期特征,而劳动呈现出逆周期特征。
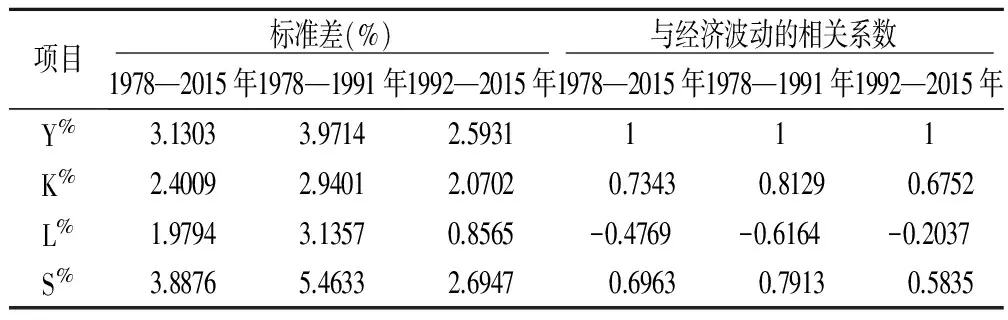
表4 经济波动、要素冲击与结构变化的描述性统计
3.4 状态空间模型下的时变参数模型分析
运用我国1978—2015年数据对式(11)进行估计,状态方程和量测方程均通过检验,得状态方程的参数估计结果见图3。若资本冲击、劳动冲击和要素结构变化冲击与经济波动之间的关系相对稳定,则图3中SV1F、SV2F、SV3F等参数应为固定值(对应固定参数模型情况),而SV1F、SV2F、SV3F等应随时间呈现为直线,但根据状态空间模型参数估计结果,三条线明显为曲线,说明资本冲击、劳动冲击和要素结构变化冲击对经济波动的影响是动态变化的。这种结果是由我国改革开放以来经济制度变化、经济结构调整和发展方式转变等多因素造成的。根据图3可见,SV1F、SV2F、SV3F等参数变化可划分为两个阶段:第一阶段(1978—1991年),SV1F、SV2F、SV3F等参数剧烈波动;第二阶段(1992—2015年),SV1F、SV2F、SV3F等参数呈有规律的变动。
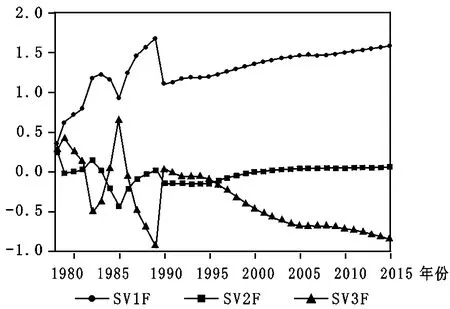
图3 状态空间模型的变参数估计值
资本冲击、劳动冲击和要素结构变化冲击对经济波动的影响两阶段的划分以1992年为界,1992年我国的市场化改革进入了一个新的阶段。1978—1991年是我国进行市场化改革的第一个阶段,这一时期我国经济要素配置的特点是资本要素稀缺,劳动要素相对丰裕,因此产出的劳动份额高于资本份额。从各要素冲击对经济波动的影响来看,资本冲击、劳动冲击和要素结构变化冲击都较剧烈,资本冲击对经济波动的贡献是较大的且呈现出在波动中上升的态势,劳动冲击对经济波动的贡献在均值为零附近上下波动,要素结构变化冲击对经济波动的贡献仅次于资本冲击且呈现出在波动中下降的趋势,说明要素结构的逐步调整有利于熨平经济波动,但其作用较小。各要素冲击波动剧烈可能与我国刚开始进行市场化改革,缺乏市场经济运作的经验和各种体制机制转变造成各要素配置的波动有关。
1992年后,我国市场化改革进入了一个新的阶段,随着经济体制改革的深化,资本要素相对稀缺的状况逐步得到改善;2008年金融危机前后,我国资本存量已逼近黄金律资本存量[18],因此这一阶段产出的资本份额比上一阶段有所提高。劳动要素方面,由于“人口红利”即将消失等因素的影响,产出的劳动份额有一定的下降。资本冲击、劳动冲击和要素结构变化冲击都呈现一定的规律性,资本冲击对经济波动的贡献是三者中最大的且为正,呈现出逐渐上升的态势,这在一定程度上与需求结构中投资的波动性最大相呼应;劳动冲击对经济波动的贡献很低接近于零,说明在这一阶段我国劳动供给是较充足的;要素结构变化冲击对经济波动的贡献与资本冲击变化趋势恰好相反,呈现逐渐下降的趋势,且在1995年后转为负值,说明要素结构变化冲击在1995年后有利于熨平经济波动,即随着经济的人均资本存量逼近人均黄金律资本存量,要素结构对经济波动的熨平效应逐步显现出来。
4 结论与政策启示
本文从增长核算和状态空间模型分析两个层面分析了我国要素投入及结构对经济增长稳定性的影响,得出如下结论:首先,各生产要素增长率的波动会直接导致经济增长的波动,劳动投入增长率波动1%,会导致经济增长率波动0.5046%;资本投入增长率波动1%,会导致经济增长率波动0.4954%,全要素生产率增长率波动1%,将导致经济增长率波动1%。其次,各要素冲击及要素结构变化对经济增长稳定性的影响体现出明显的阶段性:第一阶段(1978—1991年),资本冲击、劳动冲击和要素结构变化冲击都较剧烈,资本冲击对经济波动的贡献较大且呈现出波动中上升的态势,劳动冲击对经济波动的贡献在均值为零附近上下波动,要素结构变化冲击对经济波动的贡献仅次于资本冲击且呈现出在波动中下降的趋势,说明要素结构的逐步调整有利于熨平经济波动,但其作用较小。第二阶段(1992年至今),资本冲击、劳动冲击和要素结构变化冲击都呈现一定的规律性,资本冲击对经济波动的贡献是三者中最大的且为正,呈现一个逐渐上升的态势,劳动冲击对经济波动的贡献很低接近于零,说明在这一阶段我国劳动供给还是较充足的,要素结构变化冲击对经济波动的贡献呈逐渐下降趋势。
为确保我国经济以中高速平稳增长,基于本文的研究结论,并结合当前供给侧结构性改革的政策导向,提出如下政策启示:首先,调节要素有效供给。各生产要素的波动会导致经济增长率的波动,确保各生产要素的供给和需求进一步实现匹配,减少资源错配带来的要素波动性。提高投资的有效性,使资本投入稳步增长;落实“全面二胎”等人口政策,保证劳动要素供给;加大科技投入,实现创新驱动。其次,优化要素投入结构。要素结构变化在一定程度上起到了缓解经济波动、稳定经济增长的作用,调节生产中资本、劳动和技术结构,使生产投入向技术创新和劳动力素质提高倾斜。第三,推动供给侧结构性改革。当经济的供给和需求不匹配时,生产出的产品找不到需求时,造成产品积压,既不能形成经济增长,还会造成经济波动。减少无效和低端供给,增强供给结构对需求变化的适应性和灵活性,提高全要素生产率,使供给体系更好地适应需求结构的变化。
[1]谭鑫,赵鑫铖.产业结构调整对经济增长稳定性影响分析——以云南省为例[J].资源开发与市场,2016,32(5)∶573-577.
[2]Abramowitz Moses.Resource and Output Trends in the United States Since 1870[J].American Economic Review,1956,46(2)∶5-23.
[3]Solow Robert M.Technical Change and the Aggregate Production Function[J].Review of Economics and Statistics,1957,39(3)∶312-320.
[4]戴维·罗默.高级宏观经济学[M].北京:商务印书馆,1999.
[5]单豪杰.中国资本存量K的再估算:1952—2006年[J].数量经济技术经济研究,2008,(10)∶17-31.
[6]赵志耘,刘晓路,吕冰洋.中国要素产出弹性估计[J].经济理论与经济管理,2006,(6)∶5-11.
[7]陈彦斌,姚一旻.中国经济增长的源泉:1978—2007年[J].经济理论与经济管理,2010,(5)∶20-28.
[8]李春吉.投资冲击、全要素生产率冲击与中国经济波动——基于RBC模型估计结果的分析[J].经济问题,2010,(9)∶4-10.
[9]白强,白仲林.中国宏观经济波动源的识别与原因分析[J].统计与信息论坛,2016,(11)∶49-53.
[10]张自然,陆明涛.全要素生产率对中国地区经济增长与波动的影响[J].金融评论,2013,(1)∶7-31,123.
[11]郭庆旺,贾俊雪.中国经济波动的解释:投资冲击与全要素生产率冲击[J].管理世界,2004,(7)∶22-28.
[12]陈亮.外生冲击、要素投入变化及产出波动[D].上海:复旦大学硕士学位论文,2010.
[13]冉光和,曹跃群,钟德华.要素投入、货币供应与中国经济波动[J].管理世界,2008,(2)∶170-171.
[14]方福前,詹新宇.我国产业结构升级对经济波动的熨平效应分析[J].经济理论与经济管理,2011,(9)∶5-16.
[15]邓可斌,刘烨,汪修宇.要素投入、经济波动与增长——对资本与“主观学习”投入作用的结构模型研究[J].产业经济研究,2016,(4)∶74-86.
[16]高铁梅.计量经济分析方法与建模:EViews应用及实例(第二版)[M].北京:清华大学出版社,2009.
[17]董进.宏观经济波动周期的测度[J].经济研究,2006,(7)∶41-48.
[18]黄飞鸣.中国经济动态效率——基于消费—收入视角的检验[J].数量经济技术经济研究,2010,(4)∶3-19,106.
ResearchonInfluenceofFactorInputandStructuralChangeonStabilityofEconomicGrowth
ZHAO Xin-cheng,ZHANG Li-jun
(School of Development Studies,Yunnan University,Kunming 650091,China)
Studying on the stability of China′s economic growth from the perspective of inputs and the key elements of the supply side,had important significance for realizing the rapid and stable growth in the “13th Five-Yearquot; and the future for a long period of time.Based on the growth accounting theory and time varying parameter model,this paper analyzed the influence of factor input and structure change on economic growth and stability from two aspects:The analysis of growth accounting showed that labor input,capital input and total factor productivity growth rates were 1% fluctuation,would lead to economic growth and fluctuation 0.5046%,0.4954%,1%.The analysis based on the state space model showed that the impact of capital,labor shocks and structural changes were more severe from 1978 to 1991.The impact of capital was the mainly reason or reducing of economic stability,labor shock had little effect on the stability of the economy,and factor structure shock eased the economic fluctuation,improved the stability of economic growth since 1992.
factor input;factor structure;economic growth;growth accounting;time varying parameter model
10.3969/j.issn.1005-8141.2017.08.017
F061.2
A
1005-8141(2017)08-0985-06
2017-06-15;
2017-07-23
国家社科基金项目“最优消费率与我国经济稳定增长研究”(编号:12CJY074)。
赵鑫铖(1982-),男,云南省鹤庆人,博士,副研究员,研究方向为宏观经济运行、经济增长理论。
张利军(1977-),男,河南省新乡人,博士研究生,研究方向为宏观经济增长理论。

