恒定行和矩阵的特征值定位

何建锋

(楚雄师范学院 数学与统计学院,云南 楚雄 675000)

恒定行和矩阵的特征值定位

何建锋

(楚雄师范学院 数学与统计学院,云南 楚雄 675000)

恒定行和矩阵是指矩阵每行元素的和都为同一个数,提供了恒定行和矩阵特征值定位的一种方法并给出相关的结果,通过例子说明这种方法在矩阵特征值定位方面的有效性.

特征值;矩阵;恒定行和;Geršgorin圆盘

令e=(1,1,…,1)T,A∈Rn×n,若矩阵A每行(列)元素之和均为同一个固定常数,即有常数λ∈R,使Ae=λe(ATe=λe),则称矩阵A为恒定行(列)和矩阵.易知λ是矩阵A的一个特征徝,e为特征向量.

文献[1]中给出恒定列和矩阵特征值定位如下的一个结果.

性质1 令A为恒定列和矩阵,即有常数λ∈R,使ATe=λe,则μ∈σ(A)/{λ}也为矩阵C∶=A-diag{d1,d2,…,dn}(eeT)的特征值,其中d1,d2,…,dn∈R,σ(A)表示矩阵A的谱.

对于恒定行和矩阵A,也有类似的结果,即若有常数λ∈R,使Ae=λe,则μ∈σ(A)/{λ}也为矩阵B∶=AT-diag{d1,d2,…,dn}(eeT)的特征值,其中d1,d2,…,dn∈R.

利用文献[1]中性质1来确定恒定行(列)和矩阵的特征值定位区域,需要对参数d1,d2,…,dn∈R进行选择,结果的好坏与d1,d2,…,dn的选择有关,实际应用时很不方便.本文在第二部分中将用另一种方法给出恒定行和矩阵特征值定位的结果,所用的方法,只需知道矩阵元素即可进行计算,有其便捷性.

随机矩阵是行和为1的非负矩阵.当矩阵A为恒定行和矩阵且非负时,若行和λgt;0,则λ-1A为随机矩阵,此时对矩阵A的讨论可转化为对随机矩阵λ-1A进行,易知λ为矩阵A的主特征值.随机矩阵及其特征值定位在诸如计算机辅助设计[2]、有限Markov过程[3]、计算生物学[4]等领域都有着重要的应用.由非负矩阵的Perron-Frobenius定理[5-6]知,1是任何随机矩阵的主特征值,且e是其对应的一个特征向量.因此对于随机矩阵的特征值定位问题,只需对其所有非1特征值进行定位即可.

为了更精确的定位随机矩阵的特征值,LJ.Cvetkovic等在文献[1]中引入修正矩阵的概念,并将著名的Geršgorin圆盘定理应用于修正矩阵,得到如下随机矩阵特征值定位定理.

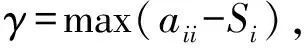
Li等在文献[7]中对定理1作了进一步改进,得到如下定理.

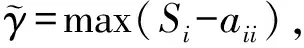
A.Banerjee等在文献[8]中给出如下结果.

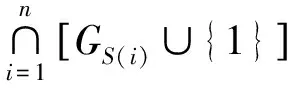
文献[8]中举例说明了在有的情况下,定理3的结果要好于定理1和定理2.本文主要讨论一般恒定行(列)和矩阵的特征值定位问题,该问题除文献[1]中有所讨论外,在其它文献中尚未见相关的讨论.在本文中,A(i|i)表示矩阵A删去第i行第i列的主子矩阵,jk=(1,1,…,1)1×k,k∈{1,2,…,n},In为n阶单位矩阵.

1 恒定行和矩阵的特征值定位

在该部分主要利用矩阵相似,讨论恒定行和矩阵的特征值定位问题.

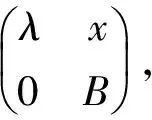
证明令α=(a21,a31,…,an1)T,

则:

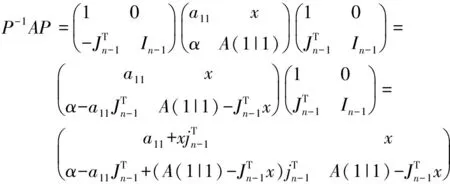
证毕.

定理5 设A=(aij)是行和恒为λ的n阶实方阵,则矩阵A除λ以外的特征值也为矩阵:

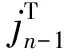
的特征值,其中α(k)=(ak1,…,ak,k-1,ak,k+1,…,akn),k=1,2,…,n.

证明k=1时,由定理4直接得结论成立.

kgt;1时,取Pk=(e2,e3,…,ek,e1,ek+1,…,en),ei=(0,…,1,…,0)T,则矩阵A相似于矩阵:

其中y=(a1k,…,ak-1,k,ak+1,k,…,ank)T.

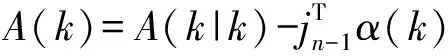
对于恒定列和矩阵也可得到与定理5相似的结论.

定理6[9](Geršgorin定理)矩阵A∈Cn×n的全体特征值都在区域:

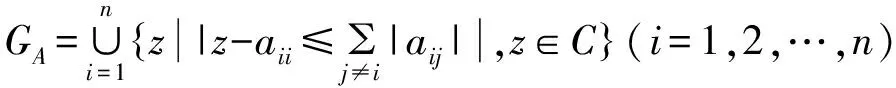
由定理5和定理6得本文的主要结论如下.

证明根据定理5的证明过程,对于任意i∈{1,2,…,n},有σ(A)=σ(A(i))∪{λ})且

证毕.

在定理7中,当矩阵A为非负矩阵,且λ=1时,即得定理3.

利用定理7,可给出恒定行和矩阵的特征值定位区域,具体例子在本文第三部分给出.

由定理6和定理7,得如下推论.

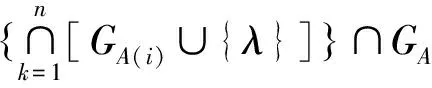
推论1给出了恒定行和矩阵的一个特征值包含区域,这个区域小于矩阵的Geršgorin区域.

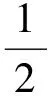
Ωij(A)={z||z-aii||z-ajj|≤RiRj,z∈C}(ilt;j;i,j=1,2,…,n)

构成的并集之中.

由定理5和定理8得如下结论.

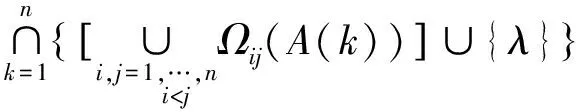
证明由定理5,∀k∈{1,2,…,n},σ(A)=σ(A(k))∪{λ}.根据定理8：

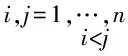
因此,

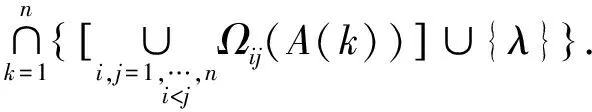
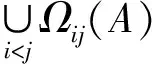
根据性质2,定理9所给的特征值定位区域要小于定理7中的区域,但定理9的计算量要比定理7的计算量大得多.

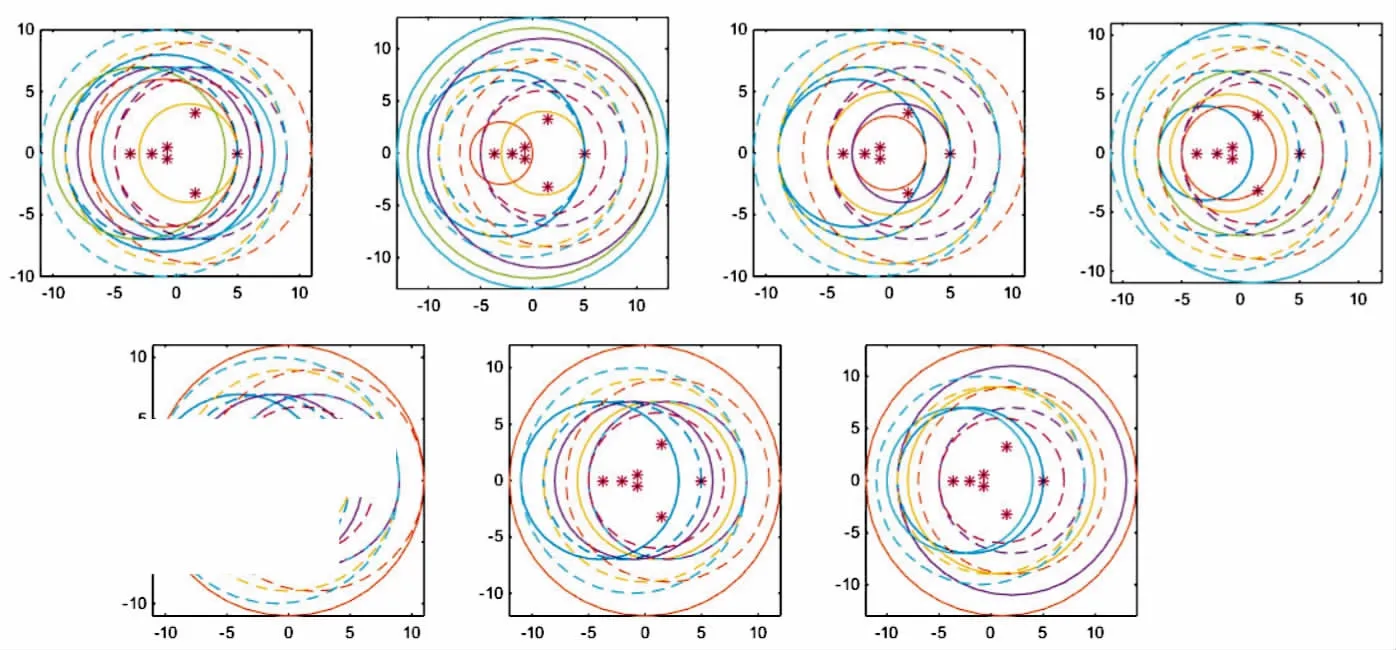
图1 GA1(i)(i=1,2,…,7)和GA1的区域Fig.1 The regions of GA1(i)(i=1,2,…,7) and GA1

2 数值算例

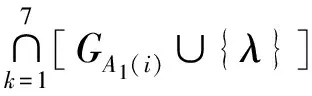
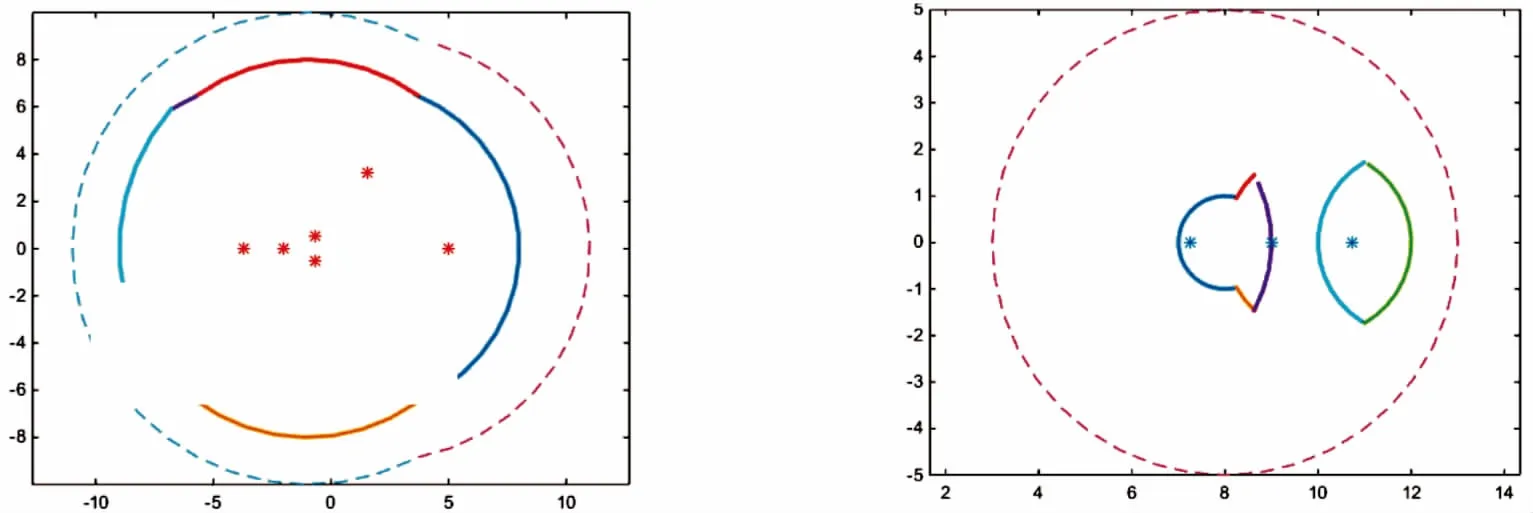
图2 区域和GA1 图3 区域和GA2 Fig.2 The regions [GA1(i)∪{λ}] and GA1 Fig.3 The regions [GA2(i)∪{λ}] and GA2

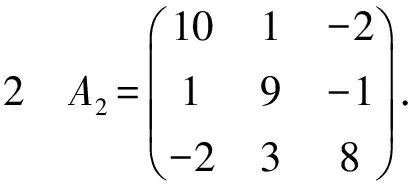
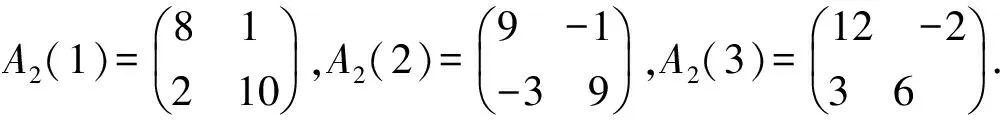
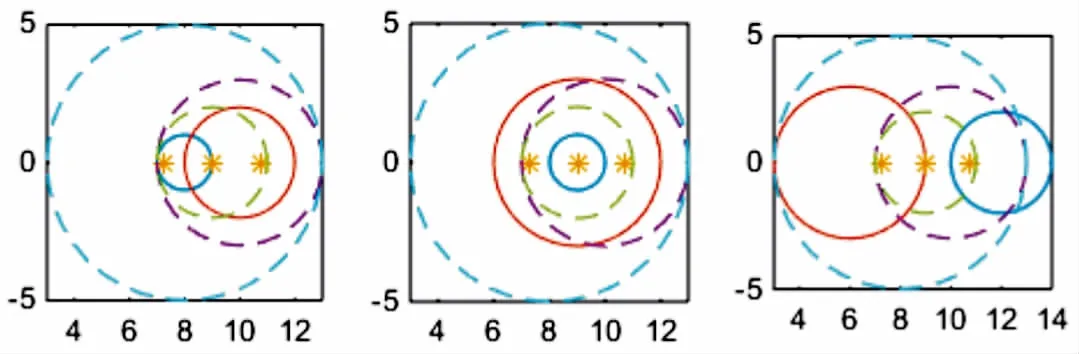
图4 区域GA2(i)(i=1,2,3)和GA2Fig.4 There regions GA2(i)(i=1,2,3) and GA2

图4显示了矩阵的Geršgorin圆盘(实线)与矩阵的Geršgorin圆盘(虚线)的位置情况.根据定理7,矩阵的特征值位于区域(见图3中的实线区域)中,该区域包含了矩阵的全部特征值,虚线圆为矩阵的Geršgorin区域,星号表示矩阵的特征值.例2直观的说明了定理7在恒定行和矩阵特征值定位中的有效性.

[3] SENETA E.Non-Negative Matrices and Markov Chains[M].Second Edition.Springer-Verlag,Heidelberg Berlin,NY,1981.

[4] NEWMAN M.Networks: an Introduction[M].Oxford University Press,NY,2010.

[5] BANERJEE A,JOST J.On the spectrum of the normalized graph Laplacian[J].Linear Algebra Appl,2008,428 (11/12) :3015-3022.

[6] BAUER F,JOST J,LIU S.Ollivier-Ricci curvature and the spectrum of the normalized graph Laplace operator[J].Math Res Lett,2012,19(6):1185-1205.

[7] LI C,LI Y.A modification of eigenvalue localization for stochastic matrices[J].Linear Algebra Appl,2014,460:231-241.

[10] 徐仲,张凯院.矩阵论简明教程[M].2版.北京:科学出版社,2005.

责任编辑：时凌

EigenvalueLocalizationforMatriceswithConstantRowSum

HE Jianfeng

(School of Mathematics and Statistics,Chuxiong Normal University,Chuxiong 675000,China)

A matrix is constant row sum if all its row sums are constant.In this paper,eigenvalue localization results and methods for matrices with constant row sum are provided,and the numerical examples are given to show the efficiency of the proposed methods in eigenvalue localization for matreces.

eigenvalue;matrix;comstant row sum;Geršgorin disk

2017-05-08.

国家自然科学基金项目(61463002).

何建锋(1974-),男,硕士,副教授,主要从事矩阵理论、图论的研究.

1008-8423(2017)04-0413-04

10.13501/j.cnki.42-1569/n.2017.12.013

O151.21

A