挠性接头细颈微细磨削仿真研究*

陈 杰，李蓓智，杨建国

(东华大学 机械工程学院，上海 201620)

挠性接头细颈微细磨削仿真研究*

陈 杰，李蓓智，杨建国

(东华大学 机械工程学院，上海 201620)

惯性导航关键件挠性接头细颈尺寸小、刚性差，在微细加工中极易变形，其精度很难控制。为了更加明确工艺参数与残余应力间的关系，充分认知细颈结构特征对残余应力分布的影响，形成更加符合细颈结构特征的相互作用机制的残余应力精确预测，以挠性接头细筋为研究对象，基于磨削加工理论、弹塑性力学和有限元等理论，利用专业金属切削软件Advantedge对残余应力进行仿真，构建了单侧及双侧磨削工艺参数对挠性接头细颈残余应力仿真模型，并分析两种模型得出的残余应力分布规律。实现了在现有条件下以加工质量为主要目标，提高加工效率为次要目标对工艺参数进行优化，为实际加工工艺参数的选择提供理论指导。

挠性接头；细颈；微细磨削；仿真

0 引言

挠性接头关键部件是厚度为50μm以下的细颈，由2个直径为1～3mm的微小孔形成，其尺寸精度要求在±1μm内，其加工质量直接影响整个惯性陀螺仪的工作性能[1-2]。细颈因为刚性差导致极易变形，加工一直面临的严峻问题是加工完成后短期及在后期使用过程中，构件会因为受到工件表面组织缺陷以及残余应力的影响而导致产品合格率极低。小孔进行精磨，对细颈的表面质量和使用性能至关重要。

阎志强，于波等人[3-4]对挠性接头制造工艺及关键技术进行了系统全面的分析，并探讨了研磨必要性。现有文献资料都局限于对挠性接头细颈加工工艺方法研究，很少有磨削工艺参数对挠性接头细颈加工质量，尤其是残余应力的作用机制研究报导。已有仿真研究多集中于构建薄壁件单侧微细磨削，对于两侧都进行微细磨削过程缺乏研究和讨论，这对于细颈双侧磨削的残余应力的生成与叠加分析具有一定的局限性。

研究克服构件变形问题，实际上就是研究减小内部应力改变其分布状态以适应结构的问题。挠性接头细颈是典型的薄壁件，其变形受多方面影响，集中体现在细颈内部应力的大小和应力分布不均匀。细颈处的应力过大或者分布不合理会使得细颈失去应有的平衡状态而产生变形[5-6]。为了维持细颈的平衡状态，应使得细颈处的残余应力分布适应其结构或减小应力。因此，本文基于有限元仿真技术，构建了单侧及考虑细颈结构特点的双侧磨削的仿真模型，分析不同工艺参数对细颈残余应力作用规律，为实际加工生产挠性接头提供理论依据。

2 单颗磨粒微细磨削仿真模型的构建

2.1 细颈微细磨削仿真运动几何模型

挠性接头细颈小孔微细磨削中，主轴转速最高可达到120000r/min，磨粒在细颈小孔上作用的时间很短，故把细颈小孔磨削简化为平面磨削。采用直径为φ2.5mm的CBN小砂轮磨削小孔直径为φ3mm的挠性接头细颈。将单颗磨粒统一假设成理想锥体，磨粒高度20μm，磨粒刃弧半径5μm，顶锥半角为53°。单颗磨粒最大未变形厚度agmax计算公式[7-9]如式(1)所示。

(1)

式中，vw为工件线速度；vs为砂轮线速度；Nd为砂轮动态有效磨刃数；θ为磨粒顶锥半角；ap为磨削深度；ds为砂轮直径；dw为工件直径。选取Advantedge软件里的二维正交微切削模块，如图1a所示为单颗磨粒磨削高弹性合金钢3J33的仿真模型；如图1b所示为磨削结束后工件自动冷却至室温，得到残余应力分布状态。

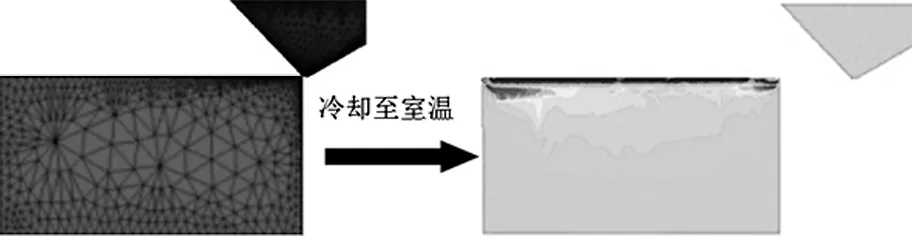
(a) 仿真模型 (b) 工件残余应力 图1 残余应力仿真模型

2.2 细颈磨削工艺参数方案

在磨削中改变砂轮线速度vs和最大未变形厚度agmax；微细磨削切削深度小，仿真中取磨削深度为1～5μm。考虑到东华大学自主研制的曲面纳米磨床高速电主轴的极限转速为120000r/min，故仿真研究中选取砂轮转速为60000～120000r/min，采用φ2.5mm小砂轮磨削，砂轮线速度范围为6.28～12.57m/s。

2.3 材料本构模型的建立

高弹性合金钢3J33是挠性接头的使用材料。砂轮磨粒材料CBN视为刚体，其物理性能参数如表1所示。

表1 工件与磨粒材料机械物理性能参数表

由于挠性接头细颈在磨削时，其材料会表现出应变率强化、应变硬化等。故在模拟微细磨削时，使用Johnson-cook模型，其数学表达式及相关参数含义为如式(2)所示[10-11]。

(2)

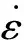
表2 3J33模型参数

2.4 网格划分

微细磨削中最小切深可达1μm，最大未变形厚度agmax至少为切深的1/10，所以最小网格可细分至0.1μm。刀具的最大网格尺寸设置为0.5μm，最小尺寸设置为0.1μm；对细颈表层40μm深度进行细分网格，网格的最大尺寸设置为5μm，最小尺寸为1μm。最终划分好的网格如图2所示。

图2 刀具、工件网格划分

2.5 细颈双侧微细磨削残余应力有限元模型构建

挠性接头关键部位细颈，其厚度仅为50μm，是典型的薄壁件，如图3所示。细颈两侧分别进行微细磨削，细颈表面及亚表面的残余应力将重新分布。本文通过在挠性接头细颈两侧微细磨削，改变工艺参数以改善残余应力分布。目前，国内外的研究最多构建细颈单侧微细磨削，对于细颈两侧都进行微细磨削后残余应力分布缺乏分析和研究。因此，通过得到的单侧磨削残余应力分布数据，以应力文件格式导入至Advantedge中，仿真计算细颈另一侧微细磨削对残余应力重新生成的影响，为提出和优化细颈双侧微细磨削加工残余应力奠定理论基础，具体流程如图4所示。

(a)实物图 (b) 细颈图图3 挠性接头细颈结构

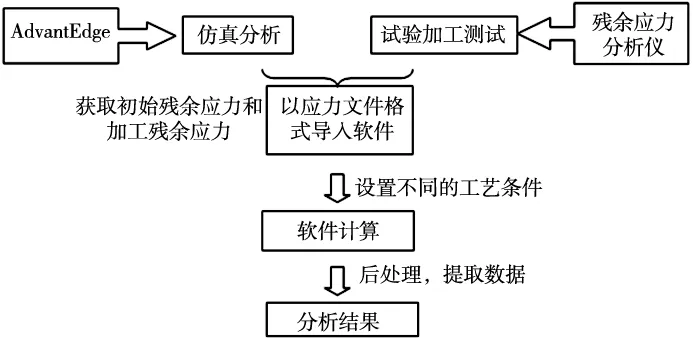
图4 细颈双侧微细磨削残余应力有限元模型构建

3 细颈微细磨削残余应力仿真结果分析

3.1单侧磨削工艺参数对挠性接头细颈残余应力的影响机制

残余应力分布见图5、图6，微细磨削作用的残余应力深度为0.034mm，在0.034mm～0.050mm范围内，细颈的残余应力趋于平衡。细颈表面残余应力为压应力(-150～-400MPa)，说明是机械效应起主要作用；亚表层为拉应力(100～300MPa)，是热效应和机械效应等共同作用的结果。

(1)砂轮线速度对残余应力影响

当保持磨削深度3μm不变时，随着砂轮线速度提高，会使细颈表面残余压应力的绝对值减小，亚表面的拉应力也减小，导致应力极差减小，拉应力深度减小。如砂轮线速度从6.28m/s增加到9.42m/s时，应力极差减小了24%；砂轮线速度从6.28m/s增加到12.57m/s时，应力极差减小了52%；应力极差减小，这对控制挠性接头的变形有利。小孔磨削因砂轮直径小，导致线速度很低情况下，仍然是较高的砂轮转速有利于控制工作表面温度和残余应力。如图5所示。

图5 砂轮线速度对残余应力影响

(2)磨削深度对残余应力影响

当保持砂轮速度9.42m/s不变时，磨削深度减小，会使细颈表面残余压应力的绝对值减小，亚表面的拉应力也减小，导致应力极差减小，拉应力深度减小。如磨削深度从5μm减小至3μm时，应力极差减小27%；磨削深度从5μm减小至1μm时，应力极差减小36%。由此可知，残余应力极差的变化程度不及磨削深度的大，提高磨削深度可以提高磨削效率，在选取加工工艺参数的时，可在细颈所允许的变形范围内选择合理的磨削深度，不仅可提高效率又可达到细颈表面质量要求。如图6所示。

图6 磨削深度对残余应力影响

3.2双侧磨削工艺参数对挠性接头细颈残余应力的影响机制

(1)细颈双侧相同工艺参数磨削对残余应力的影响

当采用和原有对应的工艺参数，即一侧细颈分别采用vs=6.28m/s，ap=3μm；vs=9.42m/s，ap=3μm和vs=12.57m/s，ap=3μm进行磨削，采用相对应参数磨削对应每一组另一侧细颈，得到的残余应力分布如图7所示。通过所得结果可知，残余应力的重新分布和原来磨削单侧后形成的残余应力分布有很大的改变。当磨削两侧细颈后，距离原有一侧细颈的表层和亚表层，残余应力由压应力变为拉应力分布；而距离新磨削一侧细颈，表层残余应力由原有的趋于平衡状态变为压应力状态分布；亚表层由原有的拉应力分布变成了压应力分布；而且压应力分布的深度范围比单侧磨削的压应力分布更深。

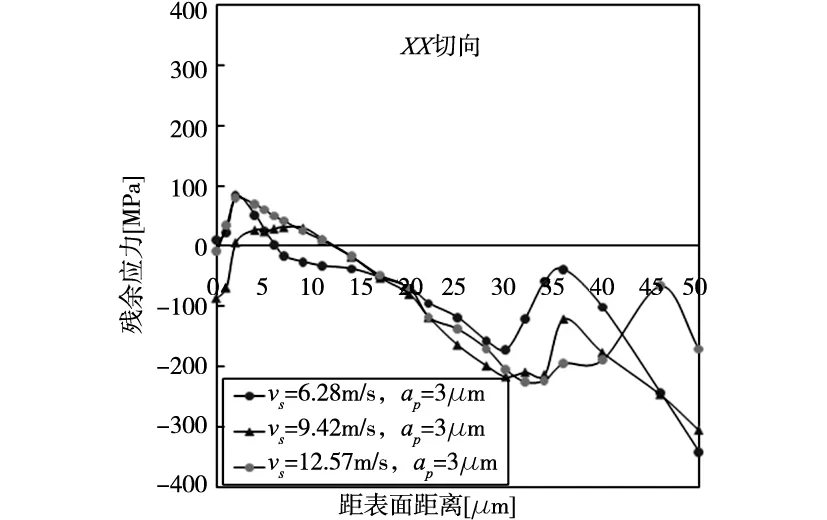
图7 细颈两侧相同工艺参数磨削对残余应力的影响

当磨削深度ap=3μm一定时，在一定砂轮线速度范围内(6.28～12.57m/s)，通过提高砂轮速度对细颈最终表面残余压应力的减小更加显著，砂轮线速度从6.28m/s增加到9.42m/s时，应力极差减小了21%；砂轮线速度从6.28m/s增加到12.57m/s时，应力极差减小了28%。

(2)细颈双侧不同工艺参数磨削对残余应力的影响

当第一侧细颈采用vs=9.42m/s，ap=3μm工艺参数进行磨削，磨削另一侧细颈分别采用vs=6.28m/s，ap=3μm以及vs=12.57m/s，ap=3μm时，并和采用和原有相同工艺参数vs=9.42m/s，ap=3μm的结果做对比，得到的残余应力分布如图8所示。

图8 细颈两侧不同工艺参数磨削对残余应力的影响

当第二侧磨削工艺参数采用高转速时，分布于细颈的残余应力极差减小。砂轮线速度从6.28m/s增加到9.42m/s时，应力极差减小了22%；砂轮线速度从6.28m/s增加到12.57m/s时，应力极差减小了40%。应力极差减小，对控制细颈变形有利。

3.3 细颈微细磨削仿真结果分析

在仅磨削一侧细颈下，如图5所示细颈表面和次表面为残余压应力分布，远次表面为残余拉应力分布，残余应力影响深度为0.034mm。当磨削两侧细颈后，如图6所示，距离原有一侧细颈的0.025mm深度范围内，残余应力变为拉应力分布；而距离新磨削一侧细颈的0.025mm深度范围内，残余应力为压应力。磨削第二侧细颈时，转速越高，可以使得整个细颈的残余应力极差更小，应力分布更趋于平衡稳定，对控制变形有利。

4 结论

基于Advantedge建立的微细磨削残余应力仿真模型，探索了不同工艺参数单侧与双侧磨削对细颈残余应力影响，可以依据零件质量要求、加工效率目标以及实际实验条件，进行微磨削工艺参数的优化设计，主要结论如下：

(1)对于首先磨削的一侧细颈，优先选用中、高速的砂轮线速度。考虑到东华大学自主研发的主轴最高转速为120000 r/min 的条件下，单侧磨削选择90000r/min，即砂轮线速度vs=9.42m/s，切深ap=3μm时磨削效率高，表面质量好，可实现质量与效率的完美统一。

(2)挠性接头细颈厚度只有50μm，难以抵抗应力的综合作用而极易变形，则可以采用适当的磨削工艺参数。在第二侧细颈磨削，优先选中、高速的砂轮线速度。如右侧细颈磨削采用vs=12.57m/s(ns=120000r/min)，ap=3μm的工艺参数，使存在细颈内部的应力大小、分布状态发生改变，达到调整应力的作用，使其适应结构，达到不产生变形或不超过希望变形量的目的。

[1] 邢文忠,张洪立,杨芸.挠性陀螺接头精密电加工技术研究[J].宇航材料工艺,2002,32(2):43-46.

[2] 刘春节,万德安. 一体式挠性接头及其制造技术[J].宇航学报,2007,28(2):475-478.

[3] 阎志强.挠性接头制造技术研究[J].航天工艺,1994(1):1-4.

[4] 于波.挠性陀螺的结构特点与制造技术[J].航空精密制造技术,1990(3):23-27.

[5] 程泽,徐九华. 单颗磨粒高速磨削镍基高温合金机理研究[D].南京:南京航空航天大学,2011.

[6] 华崇略,王贵成,刘菊东.磨削速度对工件磨削淬硬层表面残余应力分布的影响[J].机械设计与制造,2012 (4):177-178.

[7] 沈琳燕,李蓓智,杨建国.光学玻璃磨削机理的仿真研究[J].制造技术与机床,2010(2):104-106.

[8] 李蓓智. 高速高质量磨削:理论、工艺、装备与应用[M].上海: 上海科学技术出版社, 2012.

[9] 吴继华,王文奎. 微切削已加工表面残余应力预测[J].工具技术,2011,45(12):24-27.

[10] H Sasahara,T Obikaw,T Shirakashi. Prediction model of surface residual stress within a machined surface by Combining two orthogonal plane models [J] .International Journal of Machine Tool & Manufacture,2004,44(7):815-822.

[11] Jakus Adam. Modeling and simulation of the impact response of linear cellular alloys for structural energetic material applications[J].Georgia Institute of Technology,2009(4):1-30.

SimulationAnalysisforMicro-grindingFlexibleJointThinNeck

CHEN Jie, LI Bei-zhi, YANG Jian-guo

(College of Mechanical Engineering, Donghua University, Shanghai 201620, China)

The thin neck of inertial navigation key pieces flexible joints is size small and weak stiffness, the thin neck is easy to distort in the micro-grinding process, it quite difficult to control the accuracy. In order to know the relationship between process parameters and residual stress more clearly, cognitive well the structure of thin neck characteristics influence on residual stress distribution, and an accurate prediction of the residual stress of the interaction mechanism which is in line with the characteristics of the thin neck structure is obtained. Based on the theory of elastic-plastic mechanics, the residual stress distribution about the thin neck of flexible joint is obtained by using the professional cutting software Advantedge. Simulation model of residual stress about the unilateral and bilateral grinding process parameters on the thin neck of flexible joint are built up, and the residual stress distribution rule of two kinds of model are analyzed. Under the existing conditions, the first and more important is controlling the processing quality. Another one is improving the processing efficiency. All the results provide relevant theoretical basis for parameters selection in the real production.

flexible joints; thin neck; micro-grinding; simulation

1001-2265(2017)11-0116-04

10.13462/j.cnki.mmtamt.2017.11.030

2016-12-19

上海市军民融合专项(沪经信军[2016]381号)

陈杰(1989—)，男，江西宜春人，东华大学硕士研究生，研究方向为先进制造技术，(E-mail)jiechen1989@163.com；通讯作者：李蓓智(1954—)，女，上海人，东华大学教授，博士生导师，研究方向为现代集成制造技术与系统，先进制造加工、科学与技术。

TH162;TG58

A

(编辑李秀敏)