基于多目标规划算法的电梯群控系统

刘清，关榆君

( 1.华北理工大学 电气工程系，河北 唐山 063210；2.唐山学院 信息与工程系，河北 唐山 063210)

基于多目标规划算法的电梯群控系统

刘清1，关榆君2

( 1.华北理工大学 电气工程系，河北 唐山 063210；2.唐山学院 信息与工程系，河北 唐山 063210)

群控电梯；数学建模；多目标规划；最小乘梯时间；Matlab

在群控电梯设计中，算法的好坏直接影响着电梯的整体性能。算法多种多样，但各有优缺点，多目标规划算法优势明显。从时间、乘客满意度、能源消耗的角度出发，定义了包含4个评价指标的多目标评价函数，对每个评价指标进行数学建模。对多目标规划算法和最小乘梯时间算法进行程序设计，在Matlab中进行仿真分析，实验数据证明多目标规划算法综合性能优越、有很好地适应性。结果验证了多目标规划算法具有一定的实际应用性。

0 引言

电梯伴随着新算法、新技术、新思路的出现而不断升级。电梯群控系统具有多目标的特点，电梯的调度可以看作是一个寻找多目标最优解的过程。目前将群控算法结合起来分析是一大热点。例如参考文献[2]中的模糊神经网络算法，将模糊控制与神经网络两种算法结合起来应用到电梯系统中，能很好的适应交通流的变化，通过自学习来调整权值使系统优化。对多目标的群控电梯系统进行建模仿真分析，为多目标规划算法与其他算法的结合打下了基础。

1 2种电梯群控算法

1.1 群控电梯系统的多目标规划建模

初步建立以乘客的平均候梯时间AWT、平均乘梯时间ART、电梯的能源消耗ERC以及轿厢的拥挤度CRD，4个评价指标组成的评价函数如公式(1)所示。

S(i)=W1*AWT(i)+W2*ART(i)+W3*CRD(i)+W4*ERC(i)

(1)

(1) 乘客平均候梯时间AWT(i)。从乘客摁下呼梯信号开始计时到电梯到达召唤层且乘客进入电梯结束计时。包括轿厢运行时间Trun(i)和轿厢停靠时间Tstop(i)，如公式(2)所示。

AWT(i)=Trun(i)+Tstop(i)

(2)

平均候梯时间与电梯的初始状态、电梯的运行速度、停站次数和乘客进出时间及已分配的内召信号和外召信号有关。对于已分配的呼梯信号由于目的层不明确，因此统一不考虑已分配信号的目的层到站对新呼梯信号乘客候梯时间产生的影响。不再分别考虑轿厢全速及加减速运行的时间，而将运行时间简化为电梯平均通过每个楼层的时间Tr和到召唤层所经过的楼层数Nr(i)的乘积。

轿厢停靠的时间包括开关门时间和乘客出入时间，这里将总的停靠时间简化为轿厢平均停靠时间Ts和到召唤层期间停站的次数Ns(i)的乘积，如公式(3)所示。

AWT(i)=Tr*Nr(i)+Ts*Ns(i)

(3)

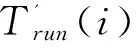
ART(i)=T'run(i)+T'stop(i)

(4)

ART(i)=Tr*N'r(i)+Ts*N's(i)

(5)

(3) 轿厢的拥挤度CRD(i)。轿厢的拥挤度可以用轿厢的乘客人数Q(i)与轿厢的容量Qmax之比来表示，其中Q(i)可以通过检测设备来获得，如公式(6)所示。

(6)

(4) 电梯能源消耗ERC(i)。电梯的能源消耗包括：起停耗能、开关门耗能、匀速运动耗能和加减速能耗等。另外，电梯轿厢运动是靠电机来拖动的，电机的起停阶段是最耗能的过程，因此主要用电梯的启停次数来衡量电梯系统的能源消耗。行梯过程中，尽量避免过多的停站。可根据电机类型，选取速度变化平缓的调速器既能满足乘客对舒适度的要求又能降低电梯的能源消耗。为了简化计算，电梯起停过程导致的启动能耗、加减速能耗、开关门能耗之和用起停能耗CS表示，电梯经过每个楼层产生的平均能耗用匀速能耗Cr表示，如公式(7)所示。

ERC(i)=Cs*Ns(i)+Cr*Nr(i)

(7)

其中，NS(i)为第i台电梯因响应内召、外召而停靠的层站数，Nr(i)为第i台电梯到达召唤层所要经过的层站数。

(5)为了方便分析和数据处理，将公式(1)中含有多种量纲的量进行无量纲化处理，如公式(8)所示。

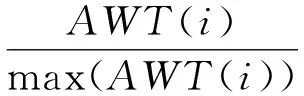
(8)

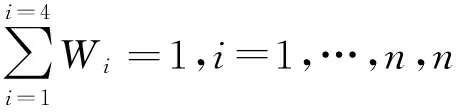
比如在空闲期，赋予W3和W4更大的权重来获得乘客的满意度和更少的能量消耗。最后比较每台电梯的评价函数值，选出最大值对应的那台电梯去响应如公式(9)所示。

S=max(S(i))

(9)

1.2 最小乘梯时间算法

最小乘梯时间算法，以时间为主要评价指标，是乘客等待电梯到来的时间和乘坐电梯到达目的楼层的时间之和。涉及到的计算公式如下所示：

T'(i)=min(T(1),T(2),…,T(n))

(10)

T(i)=Tr(i)+k(i)Toc+Tp(i),(i∈[1,n])

(11)

Tp(i)=m(i)*Te1+λδ(i)

(12)

其中，

T'(i)表示乘梯时间最小即时间最优的时间指标；

T(i)表示电梯响应召唤需要的时间；i为电梯号，n为大楼里的电梯总数；

k(i)为电梯的停靠次数；

Tp(i)表示电梯停站时乘客出入时间预测；m(i)为电梯轿厢内的乘客数；

Te为乘客进、出的平均时间；

Toc为开关门一次所需总时间；

Tr(i)表示电梯从当前层全速驶向召唤层所需的时间；

λ为调整因子；

δi为当前轿内人数与指令数之比(由数据特征化处理得到引入的目的是预测乘客进出电梯的储蓄时间，考虑乘客多，进出时间越多)。

2 仿真电梯基本运行策略

仿真电梯的运行模拟实际电梯的运行策略，首先为每台电梯设置轿厢所在位置、运行方向、已分配信号等初始数据，目的是仿真实际电梯的初始状态。

电梯根据信号指令自动行梯，到达目的层后自动停靠同时消除信号。电梯停靠时自动完成开门指令，待乘客上下完毕后立即响应乘客手动按下的关门指令，或者停靠了一定时间后电梯自动完成关门指令。停靠完毕后，若仍有未执行的召唤则继续运行，否则原地停靠待命。

不同的评价函数对应不同的性能指标导致不同的调度结果。最小乘梯时间算法实际上是时间最优算法，多目标规划算法是多种性能指标的综合考虑。

3 Matlab仿真

在Windows 7操作系统下，在matlab7.1中编写程序、对设定的两种召唤信息应用2种算法，并对仿真结果进行比较、分析。

(1)设定所有电梯的参数值如表1所示。

表1 电梯的参数值设置

(2)电梯的初始状态如表2所示。

表2 电梯初始状态

3.1 第1种情况的仿真

第1种新召唤信息：1层上行外召，目标层为12层进行仿真。

(1)多目标规划算法

(a)新外召的假设不考虑拥挤度和电梯耗能，设W1=0.5,W2=0.5,W3=0,W4=0，在第1种情况下，对应4台电梯的初始状态，获得每台的运行层数和停靠次数，利用公式得到4个评价指标的值以及综合评价函数值，得到的仿真图形如图1所示。

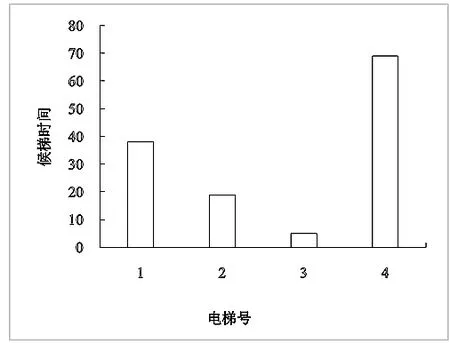
图1 多目标规划算法候梯时间仿真图

仿真结果：

S1=0.720 4，S2=0.584 4，S3=0.543 9，S4=0.948 5

乘客的平均候梯时间AWT=32.550 0，综合评价函数值S=0.543 9

(b)设置权系数为W1=0.5,W2=0.3,W3=0.1,W4=0.1。

仿真结果：

S1=0.681 8,S2=0.496 8,S3=0.497 8,S4=0.924 6

乘客的平均候梯时间AWT=32.550 0，综合评价函数值S=0.496 8

(2)最小乘梯时间算法

由于在实验条件下，乘客的拥挤度不太好预测，且实验环境客流密度相对适中，不再考虑轿内乘客人数对轿厢停靠时乘客进出轿厢时间产生的影响。并设电梯当前层上下行状态与新召唤上下行状态一致则当前层为正，反之为负。对应4台电梯的初始状态，获得每台的运行层数和开关门次数，利用公式求得每台电梯到达目的层的时间。图2所示为最小乘梯时间算法仿真图。

仿真结果：T=58.2 s

对比上面2种算法得出的结果可知，当多目标规划算法不考虑拥挤度和电梯能耗时，3号电梯的评价函数值最小，最小乘梯时间算法的仿真结果也显示3号电梯用时最短，均派3号电梯响应召唤。但是当考虑电梯拥挤度和电梯能耗时，改变了多目标规划算法的权系数时，2号电梯的评价函数值最小性能最优，宜派2号电梯响应召唤。

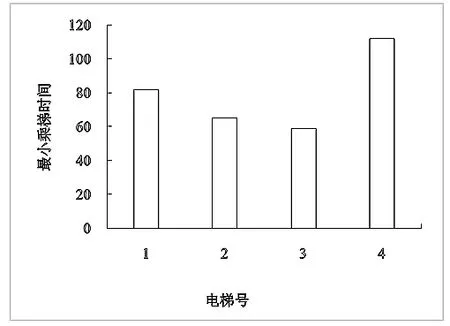
图2 最小乘梯时间算法仿真图

3.2 第2种情况的仿真

第2种新召唤信息：10层下行外召，目标层为1层

(1)多目标规划算法。设置W1=0.5,W2=0.3,W3=0.1,W4=0.1。通过计算得到各个评价指

表3 多目标规划算法下每台电梯响应召唤的数据

仿真结果：AWT=57.750 0，4号评价函数值最小。

(2)最小乘梯时间算法中得到的结果为T=62.4，4号电梯用时最少。

2种派梯结果和实际情况相吻合。

4 结论

(1)仿真情况与实际电梯运行情况保持一致，基本验证了多目标规划算法的可行性。多目标规划算法更能适应复杂环境和性能更加优越。

(2)不同的交通模式下，人们对于电梯的需求不同，可以通过改变评价目标的权重系数起到对电梯调度的目的。对于未来电梯综合性能的提升有一定的指导意义。

[1] Gu Y. Multi-objective Optimization of Multi-Agent Elevator Group Control System Based on Real-time Particle Swarm Optimization Algorithm[J]. Engineering, 2012, 04(7):368-378.

[2] 陈元琰, 邓宗明. 电梯群调度的模糊神经网络方法[J]. 计算机工程, 2003, 29(12):191-192.

[3] 杨成慧, 杨伟新, 王书文,等. 物流系统仿真研究(Ⅰ)时间最优和多目标规划算法的电梯控制[C]// The International Conference on Computational Intelligence and Industrial Application. 2010.

[4] 俞雯. 基于多目标规划算法的电梯群控系统[J]. 轻工机械, 2011, 29(5):64-67.

[5] 付丽君,周崇. 电梯群控系统的最优调度仿真[J]. 计算机仿真,2012,(04):263-267.

[6] 罗飞, 赵小翠. 新型电梯群控系统多目标优化调度策略[J]. 自动化与仪表, 2010, 25(9):28-31.

[7] 李天建. 基于多目标规划电梯群控算法的研究与设计[J]. 科学技术与工程,2010,10(28):6 883-6 888.

[8] 冯雷,张欣,张秀坤. 基于多目标进化算法的电梯群控优化调度仿真[A]. 2010系统仿真技术及其应用学术会议论文集[C].中国自动化 学会系统仿真专业委员会、中国系统仿真学会仿真技术应用专业委员会,2010:5.

[9] 邹莉. 多目标电梯群控系统的研究[J]. 自动化与仪器仪表,2010,(3):14-16.

[10] 张昆,段其昌,张从力. 基于模糊控制的多目标电梯群控技术[J]. 仪器仪表学报,2004,(s2):248-251.

[11] 王国萍,朱明富,雷科. 多目标的电梯群控系统算法分析[J]. 自动化技术与应用,2005,24(3):6-8.

ElevatorGroupControlSystemBasedonMulti-objectiveProgrammingAlgorithm

LIU Qing1, GUAN Yu-jun2

(College of Electrical Engineering, North China University of Science and Technology, Tangshan Hebei 063210, China; Department of Information and Engineering, Tangshan University, Tangshan Hebei 063210, China)

group control elevator; mathematical modeling; multi-objective programming; minimum travel time; Matlab

In the design of group control elevator, the algorithm has a direct impact on the overall performance of the elevator. The algorithm is different, but each has its own advantages and disadvantages. Multi-objective programming algorithm has obvious advantages. From the perspective of time, passenger satisfaction and energy consumption. The multi-objective evaluation function including 4 evaluation indexes is defined. Mathematical modeling and analysis of each evaluation target. The multi-objective programming algorithm and the minimum ride time algorithm are designed and simulated in Matlab. The experimental data show that the multi-objective programming algorithm has excellent comprehensive performance and good adaptability. The results show that the multi-objective programming algorithm has certain practical applicability.

2095-2716(2017)04-0088-06

2017-05-06

2017-09-16

TP273

A