基于离散和连续型算法的报废汽车拆解中心选址对比研究

文/符杰 周自强 黄艰生 应文豪（.江苏华宏科技股份有限公司，江苏江阴 443；.常熟理工学院，江苏常熟 5500江苏省重大成果转化项目；项目编号：BA04067）

基于离散和连续型算法的报废汽车拆解中心选址对比研究

Research on location for end-of-life vehicles based on disperse and continuous model.

文/符杰1周自强2黄艰生1应文豪2（1.江苏华宏科技股份有限公司，江苏江阴 214423；2.常熟理工学院，江苏常熟 215500江苏省重大成果转化项目；项目编号：BA2014067）

针对报废汽车拆解中心的选址问题，本文以江苏省报废汽车和公路运输的实际状况为算例，提供了离散型和连续型两种不同的建模思路，并分别进行了求解。对于连续型模型采用了Matlab优化工具箱中的非线性规划函数对模型进行了计算，两种模型的计算结果高度吻合，因此在基础数据不全的情况下，可采用连续式模型代替离散型模型进行选址规划，这对于物流企业优化选择具有积极意义。

报废汽车； 选址规划；离散型模型；连续型模型

1 引言

随着经济的快速发展,我国汽车的产、销量每年都在大幅度提高，根据国家统计局的统计，至2012年12月，我国汽车年产销量已达到1900万辆，保有量12089万辆,报废注销量达451.64万辆。按照我国《汽车报废标准》，我国报废汽车的数量也在快速增长，据相关机构预测，至2020年，我国的报废汽车数量将达到600万辆/年[1]。随着我国报废汽车处理政策不断加强和完善，必然引导拆解企业向规范化、专业化、规模化、集约化发展。由于报废汽车拆解回收基地投资高，年处理量大，业务辐射范围广，运输费在生产成本中占比较高，因此合理选址是保障基地高效运营的前提，决定了企业的发展前景。

李卫江[2]应用Matlab的优化函数求解了带有时效性约束的物流中心选址问题，魏光兴[3]通过对物流选址常用的连续型重心法自由度过多问题，提出了一种多权重的离散型算法。本文以江苏省报废汽车拆解基地为研究对象，通过基于现实的离散型模型和基于理想化的连续型模型的对比分析，为报废汽车基地选址规划提供借鉴。

储江伟[4]通过对年拆2万辆的报废汽车拆解厂测算，一年的运营成本为6815.9万元，每辆车的重量为1193kg，拆解后材料销售收入为8730万元，则拆解收益为957元/辆。

2 离散型选址模型的建立

报废汽车拆解基地的选址的目标为运营的收益最大。其数学模型如下：

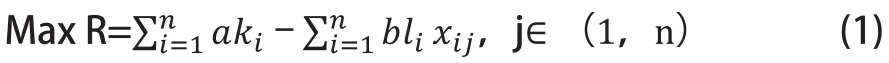
其中a为每辆车的拆解收益；ki为某个城市的回收量（辆）；b为运输单价，2011年5月份全国公路货物运输市场价格为0.303CNY/（t Km）；li为某个城市的回收量（t）；xij为某个城市到拆解基地的距离（Km）。

采用离散化模型进行分析计算，即根据实际情况，每个点作为现实中存在的城市，城市与城市之间的运输距离不是地图上的直线距离，而是来源于实际的公路体系，江苏省各城市的公路间距离和每个城市的汽车保有量的可通过《江苏统计年鉴》整理得到。

世界通用的报废汽车比率为保有量的6%，而我国现阶段依法报废的汽车最多只占到应报废汽车总量的40%。

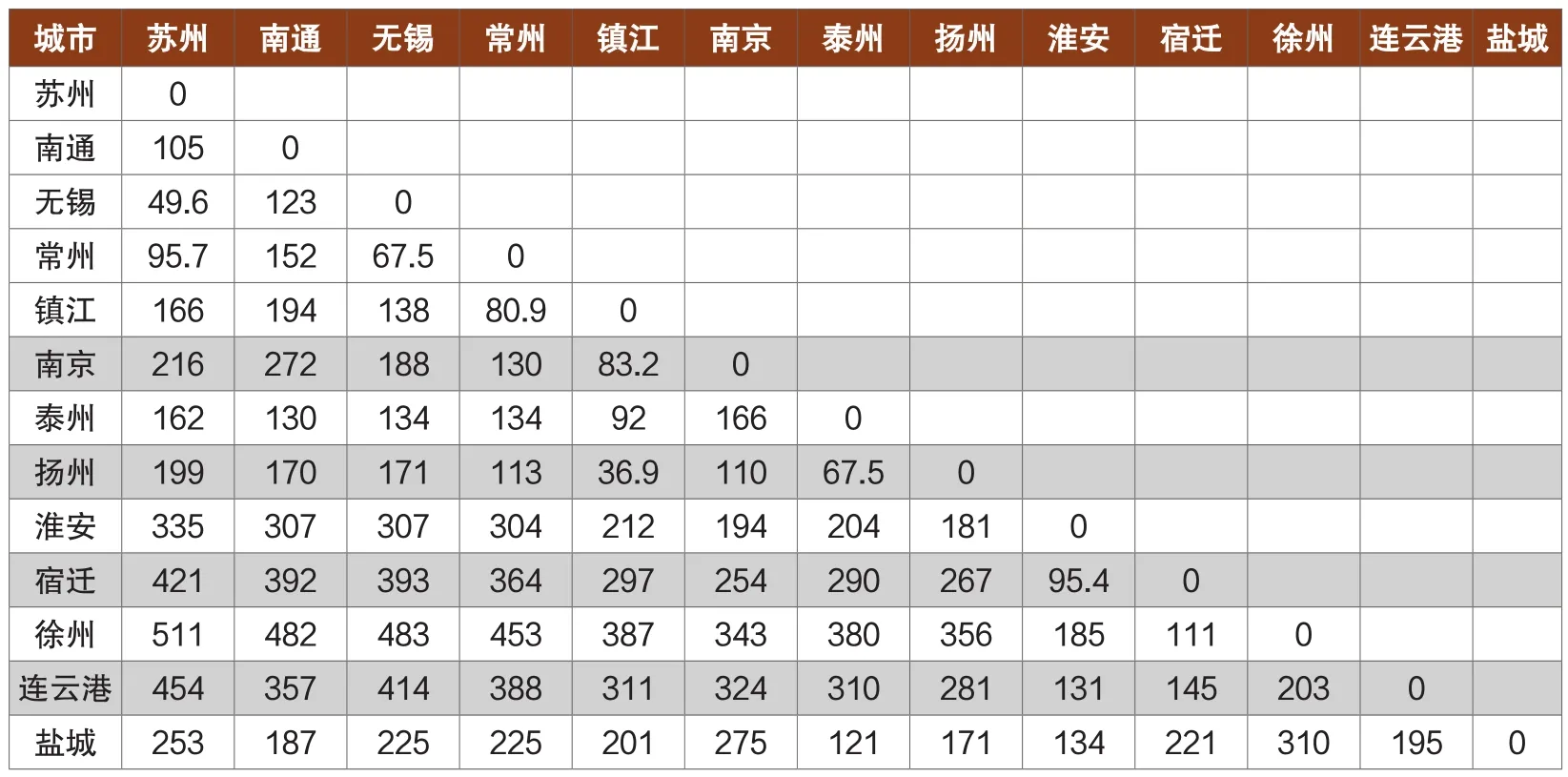
表1 江苏各城市公路之间的实际距离

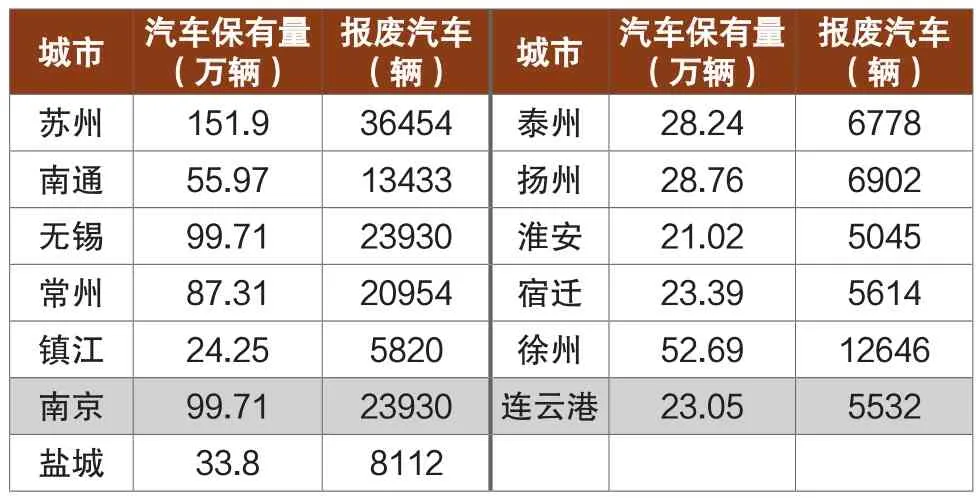
表2 每个城市的报废汽车数量

将基础数据代入式（1）计算，即可得到每个城市分部拆解基地的运营收益。

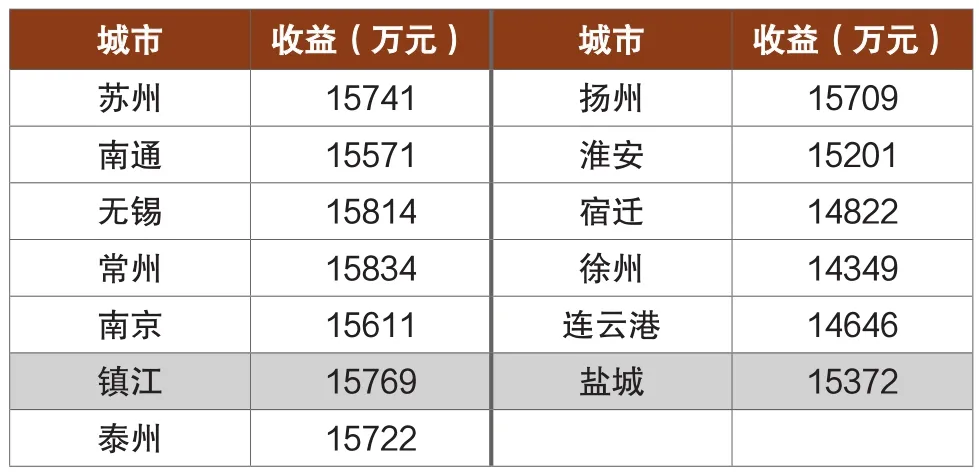
表3 报废汽车拆解基地分布在不同城市的运营收益

因此，将报废汽车拆解基地设在常州市，运营效益最大，为15834万元，将基地设置在徐州，运营效益最小，为14349万元，比常州低9.4%。

3 连续型选址模型的建立与分析

连续性选址一般做如下假设[5]：①选址目标区域是连续的，区域内任意一点都是候选地点；②用两点间的直线距离近似代替两点间的运算距离。因此本文直接以整个江苏省的地域为边界条件，在其内部连续的寻址，使得目标函数取得最大值。

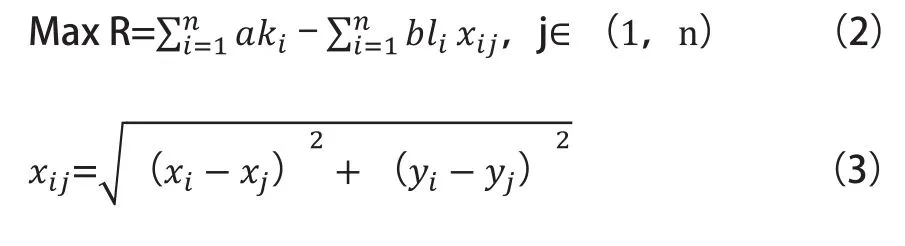
将实际模型转化为适合Matlab求解的优化函数：

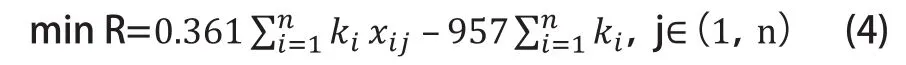
为了连续型模型的计算，需将其统一到一个二维的坐标系中，而每个城市在地理上均有其自己的GPS坐标，这是一个球坐标，对于本技术模型，需将其转化为统一的平面坐标系。为简化计算过程，本项目拟采用成熟的商用数字地图技术，城市间的距离直接采用地图自带的测距工具测量，然后以底部苏州市的纵坐标和徐州市的横坐标作为坐标原点，获得每个城市的相对坐标。

从式（4）可知，本选址模型是一个带边界约束的非线性规划的求最小值问题，可以利用Matlab优化工具箱中函数直接求解。fmincon( )函数是有约束的非线性最小化的函数，适用于本模型的优化计算。

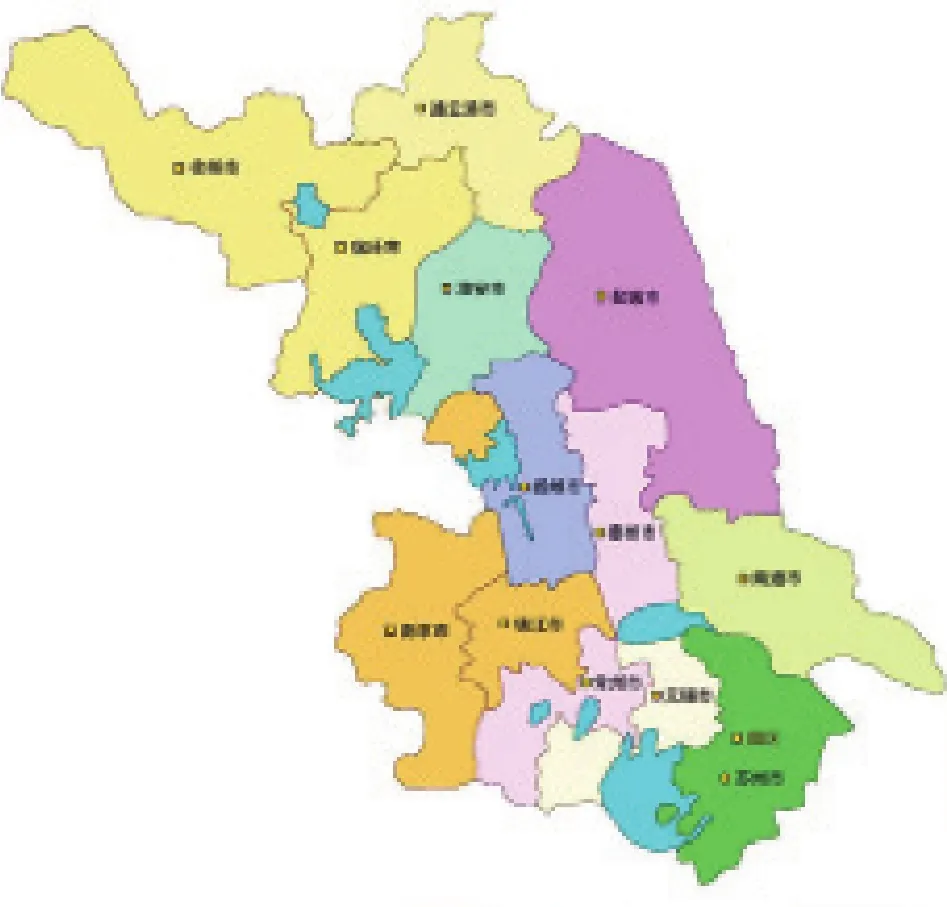
图1 江苏省城市地图

表4 每个城市的相对坐标

fmincon( )的标准数学模型为：

式中：x、b、beq、lb、ub为向量；A、Aeq为矩阵；c(x)、ceq(x)为函数[6]。因此连续型选址模型和fmincon( )的标准数学模型：

其中：输出函数中，x为选址结果，fval为函数目标值；fun为编写目标函数的M文件；x0为初值, A、b、Aeq、beq为线性约束，为空集,lb、ub为上下限。

初始点选用系统自动生成的随机数，即x0=100 rand(2,1)

经过Matlab优化计算，得到选址中心坐标为[250.4242,58.6810]，处于常州市的范围。此时运行效益达到最大，为16044万元。

4 结束语

将上述离散型和连续型选址模型的计算进行比较可知，连续型模型和离散型模型选址结果十分吻合，由于连续型模型计算距离时默认假设为两点的直线距离，因此其计算得到的运行效益比离散型模型的结果高1.3%，符合现实逻辑。由于离散型选址计算需要大量的基础数据支撑，而连续型选址模型只需要电子地图，随处可得，且本文中编写的M文件可以通用，十分便捷，为解决同类问题提供了一种十分有效的解决方案，具有十分积极的意义。

[1] 周自强,戴国洪,谭翰墨. 报废汽车拆解与回收技术的发展与研究现状 [J]. 常熟理工学院学报, 2011,10: 107-111.

[2] 李卫江,郭晓汾,张毅,等. 基于Matlab优化算法的物流中心选址 [J]. 长安大学学报, 2006,26（3）: 76-79.

[3] 魏光兴. 物流配送中心选址的一个离散模型研究 [J]. 重庆交通学院学报, 2006,25（4）: 124-127.

[4] 储江伟,夏秀清,强添纲,李洪亮. 报废汽车拆解厂建设投资案例的经济效益分析 [J]. 再生利用,2013，6（2）40-42.

[5] 蔡临林.物流系统规划—建模及实例分析[M].北京：机械工业出版社,2003.

[6] 苏金明,阮沈勇.Matlab6.1实用指南[M]. 北京：电子工业出版社,2002.

F224

A