有界单连通区域上解析逆紧映射的拓扑度

戴作科+董新汉

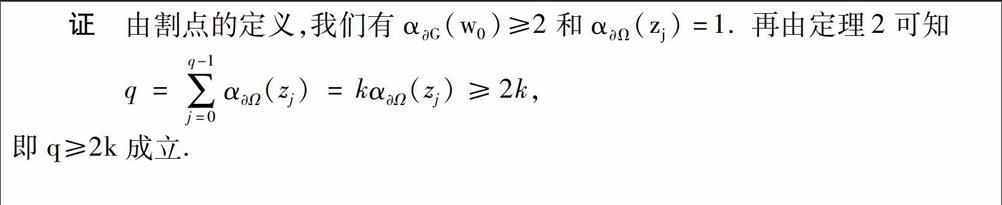
摘 要 设Ω和G都是边界局部连通的有界单连通区域，假设f是Ω到G的解析逆紧映射. 通过将单连通区域提升至单位圆盘，本文得到了G的边界点的分支数和其逆象点分支数之间的等式关系，并讨论了f的拓扑度和逆象点个数之间的不等式关系.

关键词 割点；拓扑度；分支数

中图分类号 G420； O174.5 文献标识码 A 文章编号 1000-2537（2017）05-0077-03

Topological Degree of Proper Holomorphic Mapping on Bounded Simply Connected Domains

DAI Zuo-ke， DONG Xin-han

（College of Mathematics and Computer Science， Hunan Normal University， Changsha 410081， China）

Abstract Letting Ω and G be two simply connected domains with locally connected boundary， letting f be a proper holomorphic mapping from Ω onto G， and lifting Ω and G onto unit discs， in this work， we have obtained the equality relationship between component numbers of the point on G and those of its different inverse image points on G. The inequality relationship between the topological degree of f and the number of the different inverse image points is also obtained and discussed.

Key words cut point； topological degree； component number

假設X和Y是两个拓扑空间，令Ω和G分别为X和Y中的两个子集，f：Ω→G为一个连续映射，如果G中每个紧子集的逆象集都是Ω中的紧集，则称f是Ω到G的逆紧映射[1]. 在分形几何与复分析的交叉研究中[2-6]，Cantor边界性质的专题研究必须借助全纯逆紧映射的性质. 对一般解析函数（非逆紧），其定义域边界的象集分全平面C为若干个连通分支，则相关连通分支的个数、拓扑度和判别点个数又紧密联系着. 著名的Riemann-Hurwitz公式阐述了这个联系[7]. 为了更深入揭示Cantor边界性质中Cantor集C的性质，我们需要边界上割点的重数[8]和连通分支上的拓扑度之间的联系. 本文的目的就是刻画这种联系，至于它的应用我们将另文给出.

多于一点的连通紧集称为连续统，它包含有不可数多个点. 令E为一个局部连通的连续统，对于a∈E，如果E＼{a}不连通，则称a为E的割点[8]. 令Ω为一个有界的区域，记由在Ω上解析且在上连续的函数构成的空间为A（Ω），赋予上确界范数，A（Ω）是一个Banach空间. 对于FΩ，记方程f（z）=w在F中的根的个数为nf（w，F），根的个数按重数计算.

参考文献：

[1] RUDIN W. Function theory in the unit ball of Cn [M]. New York： Springer Verlag， 1980.

[2] DONG X H， LAU K S. Cantor boundary behavior of analytic functions. Recent development in fractals and related fields[J]. Birkhuser， 2010，232（1）：283-294.

[3] DONG X H， LAU K S， LIU J C. Cantor boundary behavior of analytic functions[J]. Adv Math， 2013，232（1）：543-570.

[4] DONG X H， LAU K S， WU H H. Cauchy transform of self-similar measures： Starlikeness and univalence[J]. Trans Am Math Soc， 2017，369（7）：4817-4842.

[5] DONG X H， LAU K S. Cauchy transforms of self-similar measures： the Laurent coefficients[J]. J Funct Anal， 2003，202（1）：67-97.

[6] DONG X H， LAU K S. An integral related to the Cauchy transform on the Sierpinski gasket[J]. Exp Math， 2004，13（4）：415-419.

[7] TEINMETZ N S. The formula of Riemann-Hurwitz and iteration of rational functions[J]. Complex Variables Theory Appl， 1993，22（3）：203-206.

[8] POMMERENKE C. Boundary behaviour of conformal maps [M]. New York：Springer Verlag， 1992.endprint