模数转换器（ADC）性能对雷达系统的影响性分析∗

任圣君 陈少昌

（海军工程大学电子工程学院 武汉 430033）

模数转换器（ADC）性能对雷达系统的影响性分析∗

任圣君 陈少昌

（海军工程大学电子工程学院 武汉 430033）

在软件化雷达实现的过程中，模数转换器扮演着极其重要的角色，它是连接模拟世界和数字世界的唯一桥梁，是模拟电路和数字电路的分水岭，是雷达信号进入数字化处理的关键一步。因此，ADC的性能会对雷达的信号处理、检测估计等过程产生直接影响，对软件雷达的实现起到至关重要的作用。文章就针对模数转换器的速度、精度等性能对后续雷达信号处理的影响进行评估分析。利用Matlab软件进行数据仿真，模拟ADC在采样、量化过程中的一系列性能指标，着重分析模数转换过程中的量化噪声以及时钟抖动对雷达系统的影响，包括对信噪比的影响，雷达威力范围的影响等。最终通过仿真分析验证了理论的正确性。

模数转换器；量化噪声；时钟抖动；软件化雷达

1 引言

模数转换器是决定接收信号性能的最重要环节之一，它完成接收信号从模拟域到数字域的变换。它是连接模拟世界和数字世界的唯一桥梁。随着电子技术的飞速发展，高速高精度ADC的性能得到不断提升，使得雷达信号数字化处理的程度不断提高，软件化雷达的实现也成为可能。软件化雷达的思想是将模数转换器尽可能靠近天线，最理想的情况是将天线感应到的信号经过滤波、放大后直接转换成数字信号，即实现射频直接采样［1］。那么ADC的性能会怎样影响雷达信号的数据处理呢？

在目前的采样系统中，采样时钟的抖动问题是一个关键问题。文章研究了带通采样时钟抖动对系统的影响，分析采样时钟沿抖动对雷达性能的影响，并通过仿真验证了理论分析的正确性。

2 ADC的主要性能指标

实际应用时，由于ADC并不是理想的ADC，会存在不同的采样误差以及通道失配误差［2］。所以我们在使用时要根据不同的应用需要来选择不同的性能的ADC。首先介绍一下ADC各种性能指标，分别是：分辨率、转换速度、相对精度、量化误差、满刻度误差、偏移误差、线性度。还有一些其他的指标，例如：绝对精度、微分非线性、积分非线性、总谐波失真等。

2.1 分辨率

ADC的分辨率是指ADC输出数字量的位数，位数越高可以将信号量化的份数就越多，理论上的采样精度越高，是一种对输入信号的辨别能力。对于二进制的N位分辨率的ADC所能分辨的最小量化信号或量化电平的能力为2N个。如果ADC的输入范围是0-Vref，那么这个ADC能分辨的最小电平为Vref∕2N。

2.2 转换速度

转换速度是指ADC完成一次由输入信号完完全全转换到数字信号的时间的倒数。她也通常被称为采样速率，表示每秒钟对信号采样的次数。常用的单位是ksps和Msps。

2.3 量化误差

量化误差是由于采样过程中量化输入信号带来的误差，实际上是因为A∕D转换器做工等引起的有限分辨率，进而引起量化误差。

2.4 动态范围

ADC的动态范围是指ADC正常工作时可以接受的信号幅度的范围。ADC的最大幅度和最小幅度的比值，用dB表示。

3 采样时钟抖动与量化噪声对接收信号的影响的理论分析

采样时钟的抖动是时钟源的固有性质，是不可避免的，尤其是在高速射频采样时由于抖动给采样信号带来的影响就显得尤为明显［3］。下面将从抖动的产生以及对信号采样产生的影响两个方面展开。

3.1 时钟抖动的产生

时钟抖动可以理解为信号偏离了理想位置的短期变化程度，一般用时间单位来表示。当时钟边沿到来时刻偏离了理想时刻的时候，会造成采样点的不确定性［4～5］。如果仍然以标定的采样间隔对信号进行采样的话就必然会由于孔径抖动误差而产生噪声，严重情况下会引起系统信噪比的急剧下降。

由图1可以看到时钟抖动误差的存在，其中δt表示理想采样点与实际采样点之间的偏差，其值为可正可负，通常情况可以把δt看作一个服从N(0,δt2)的高斯分布的随机变量［6～7］。 e(t)表示由于时钟抖动偏差的存在而造成的采样值与理想值之间的采样误差。

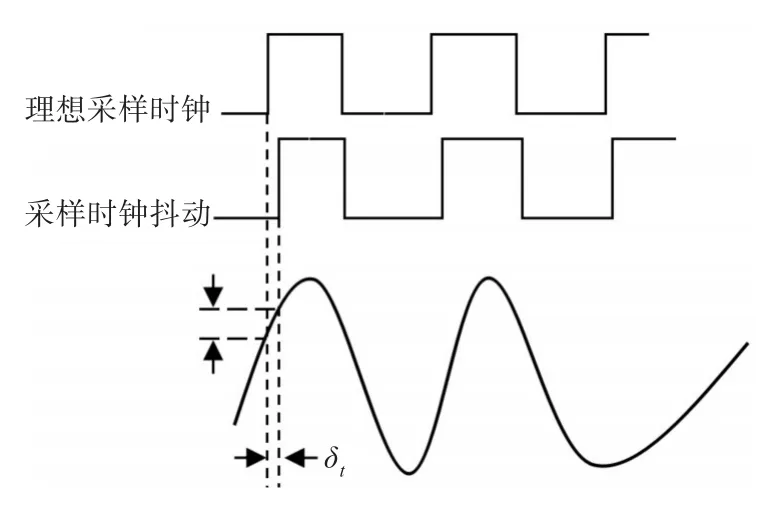
图1 时钟抖动误差示意图

3.2 时钟抖动误差分析

在ADC的采样中，由于时钟抖动产生的误差可以转化为相位噪声，即将采样过程中时钟的抖动看作是对窄带信号做相位调制。下面我们来探究相位噪声与时钟抖动之间的关系，假设在没有时钟抖动的情况下的采样相位为

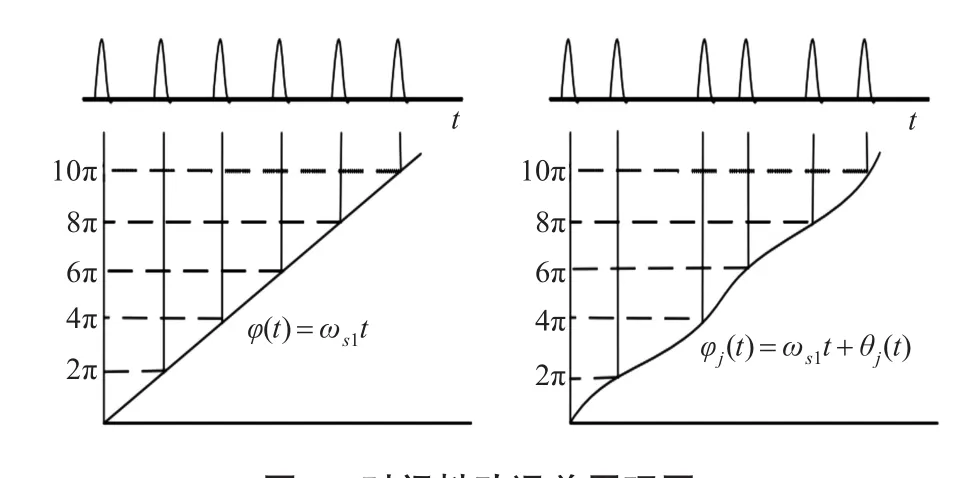
图2 时间抖动误差原理图

当t=kTs时，相位φ(t)以2π的整数倍出现。右图表示当采样时钟有抖动时采样得到的信号的相位调制信息，由于抖动的存在造成的采样点的采样时间变为t=kTs+δt。用θj(t)表示由于采样时钟的不稳定而造成的时钟相位的偏差［8］。相对于理想采样，抖动下的时钟相位调制多了个θj(t)部分，即

假设接收机接收到的射频信号为

如果没有抖动的存在，理想的采样后的输出信号y(t)较之原始信号相同，不同的只是载频发生改变，即

由于采样的过程会使得频谱以采样频率为周期进行搬移，所以采样后需要经过插值滤波器选频。其中，，表示采样后的插值滤波器选频出的采样信号中频位置。β=sgn(ωc-kωs1)，表示信号是否因奇偶奈奎斯特区间的不同而发生频谱反转。β=-1时代表信号的频谱发生了反转，而β=1则表示信号的频谱没有反转。kH=round(ωc/ωs1)为插值滤波器所选择的采样后信号谐波分量值，其大小为ωcωs1的四舍五入取整值。

但是在实际采样过程中由于采样时钟脉冲的抖动，导致采样输出信号与理想采样信号之间存在相位差 yj(t)为

式中，θj(t)表示由于采样抖动而使信号相位出现的扰动。。从上式中也可以看到输出信号的相位扰动大小也与抖动调制因子有关，即使射频输入信号下变频到中频时的采样时钟谐波分量有关。

用e(t)表示由于抖动引起的输出信号误差，则有：

由于一般情况下，由时钟抖动引起的相位误差θj(t)相对于信号原本的相位来说很小，所以有：

由以上的分析可以看出由于时钟抖动产生的信号误差e(t)与θj(t)是呈正比例的关系，并且误差的平均功率也随θj(t)方差的增大即抖动的剧烈而增大。

平均功率误差表示为

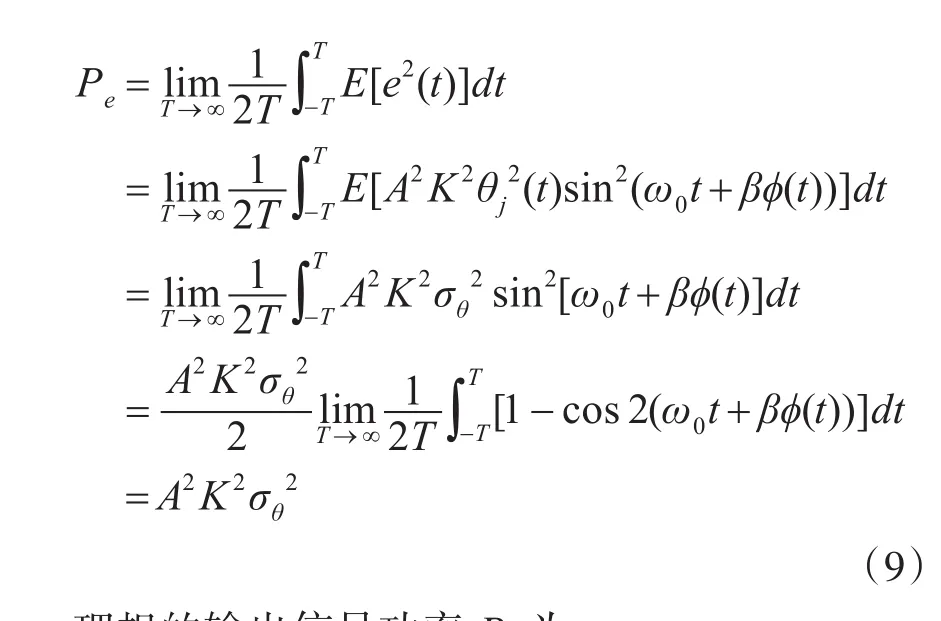
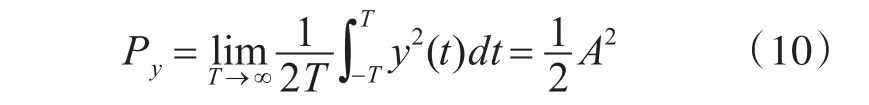
所以在只考虑由于射频采样时钟的抖动引起的信号信噪比可以表示为

理想的输出信号功率Py为

3.3 量化噪声与理论信噪比

理论上，由于ADC将信号的离散化处理导致在量化的过程中必然引入量化误差，又称为量化噪声。ADC的量化噪声将会对信噪比产生影响，对于N位精度的ADC，设它的量化噪声范围为(-Δ/2,Δ/2)，其中Δ=1LSB。则噪声总功率为

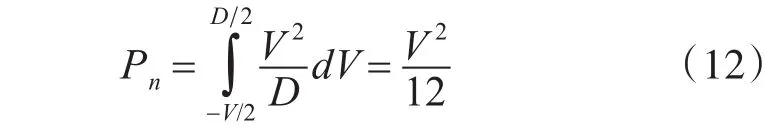
最大输入信号幅度为2N×Δ，则最大信号功率为

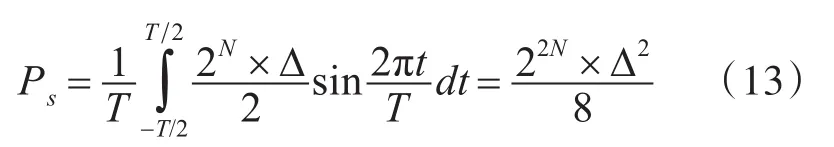
又因为

3.4 雷达测距的理论精度与信噪比的关系

根据雷达测距的原理，雷达的距离测量精度与许多因素有关，理论上和信号传播的速度，传播路径，传播时间都有一定的联系［9～11］。但是实际在信号处理中距离测量主要是对测量发射脉冲和接收脉冲的延迟时间精确测量。由于在实际信号的信号脉冲有一定的宽度，并且不是理想的，因此会有比较宽的上升沿和下降沿，加之信号的处理中无法消除的各类噪声的影响，判断信号的准确到达时间是十分困难的事情，大多需要根据统计规律在理论上进行估计［12］。由噪声引起的测量误差通常称为测量的理论精度或极限精度。

4 ADC性能仿真分析

利用Matlab软件对雷达信号处理过程进行仿真，分析ADC性能对信号处理与信号检测的影响。首先以单频信号为例，选取美军的AN∕SPS-6舰载对空搜索雷达［13］（世界海用雷达手册229-230），其主要性能参数如下。

雷达信号的载频为1250 MHz～1350MHz，脉冲重复频率为600Hz，即重复周期为1.67ms，脉冲宽度为1μs，中频频率为30MHz。以1.3GHz的余弦单频信号为基础进行时钟抖动采样的仿真分析，研究对信噪比影响。选取ADC采样频率为3GHz，分辨率为12位。

4.1 量化噪声对信号处理的影响

由于信号转换成数字信号的过程中经过采样量化，理论上会不可避免地产生量化误差，并且误差的大小和ADC的量化量化位数有关系［14］。文章选取12位的模数转换器进行分析，可以将2V的电压分成2^12=4096个量化单元，信号采集点上的信号幅度与哪一个更接近就取为该二进制数。

最小量化单元2∕4096=4.88e-04，也就是信号量化产生误差的最大值。信号量化前后的误差变化如图3所示。

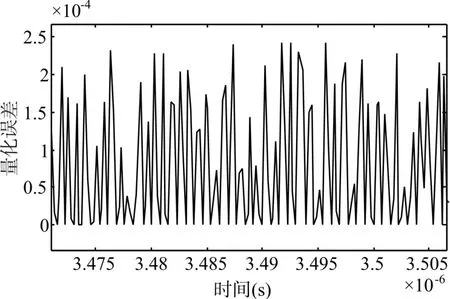
图3 量化误差

由于信号量化产生的误差均值为8.141e-05。通过计算信号的能量，与量化噪声的能量相比，得到量化噪声的信噪比为SNR=74.0061dB。

由式（15）可以得到12位ADC的量化噪声的信噪比为74dB，仿真结果与理论计算值吻合。下面改变不同的量化位数，观察信噪比的变化情况。

从图4中可以看到，仿真的结果图像体现了信噪比与分辨率位数的标准的线性关系。很好地印证了理论的正确性。

4.2 时间抖动引起的相位噪声对信号处理的影响

利用Matlab对时钟抖动进行仿真，在采样的时间点上加入高斯白噪声，噪声均值为零，方差为3ps，下面是加入时钟抖动后的信号的频谱。

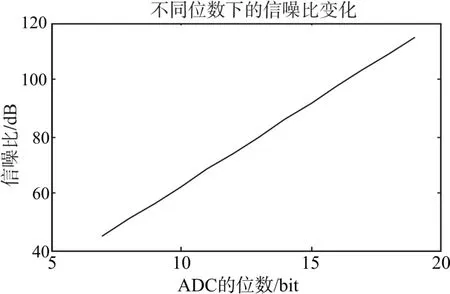
图4 ADC位数与信噪比的关系

图5 含有时间抖动误差的信号频谱

从频谱图中看信号的变化不是很明显，下面将信号的幅度归一化为dB值，可以清晰地看到加入时钟抖动前后的相位噪声的产生。

图6 时钟抖动误差归一化频谱对比

图6显示在时间抖动均方根在3ps的情况下在信号的频谱中能明显地看到相位噪声的存在。

下面我们将信号抖动前后的幅度相减，得到抖动产生的误差如下图7所示。

图7 时域和频域的量化误差

由图7中可以看出，时间抖动产生的随机误差在正负0.08以内，并且在频域上大致均匀的分布在各个频段。由此计算得到时间抖动引起的信噪比为32.23dB。改变不同时间抖动的大小，从0.1ps～20ps，观察信噪比的变化，如图8所示。

图8 时间抖动与信噪比的关系

在时钟抖动的理论研究中，我们理论证明了由于采样时钟抖动影响产生的噪声的能量和时钟抖动的方差成正比，即：

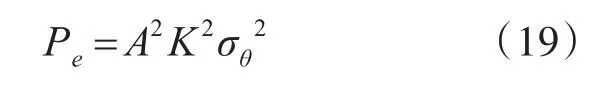
并且由此得到

这与仿真得到的图像相吻合。信噪比随时间抖动的方差呈对数函数变化。

4.3 ADC性能对雷达探测距离的影响分析

距离测量是雷达的首要任务，也是一切功能的基础，雷达的最大探测距离是雷达的基本方程，如下式：

式中，Pt为雷达的发射功率，G为天线增益，λ为信号的波长，σ为目标散射面积（RCS），k为波尔兹曼常数，T0为标准室温，一般取290K，B为接收机带宽，F为接收机的噪声系数，L为表示雷达其他各部分的损耗。(S/N)omin是最小输出信噪比，也成为识别系数或检测因子（Detectability Factor），用 D0表示。

给定雷达的发射功率，天线增益等重要参数，并且在其他条件都理想的情况下，只针对ADC的性能进行分析。ADC的参数变化能够影响接收机的性能，体现在雷达方程中，影响雷达的最大探测距离的因子就是检测因子D0，即接收机的输出信噪比［15］。

下面我们通过对雷达系统信号处理的方针，计算一部雷达的理论最大探测距离，并分析ADC的不同的参数设置对雷达探测距离的影响。对于脉冲雷达而言，设发射功率为1kw，载频为1.3GHz，脉冲宽度为2μs，天线增益取38dB，根据天线辐射能量的分布做出下面的雷达威力图，图9中表示了雷达在不同方向上的最大探测距离，由于天线在不同的方向上辐射的能量不同，因此雷达威力图一定程度上反映了天线的方向图。

图9 雷达威力示意图

如图9所示，黑色的曲线表示雷达在不同方位上的威力范围的大小，上面的点到原点的距离表示雷达在该方向上的理论最大探测距离。

在上面的讨论中我们得到了ADC的时间抖动和量化误差对信噪比的影响，这会影响接收的输出信噪比，即影响检测因子D0，从而会对雷达的探测距离造成影响，为了方便研究，我们取雷达威力图的最大值为雷达的最大探测距离。加入上述讨论中ADC的时间抖动以及量化误差对信噪比的影响，得到ADC性能对雷达最大探测距离的影响。

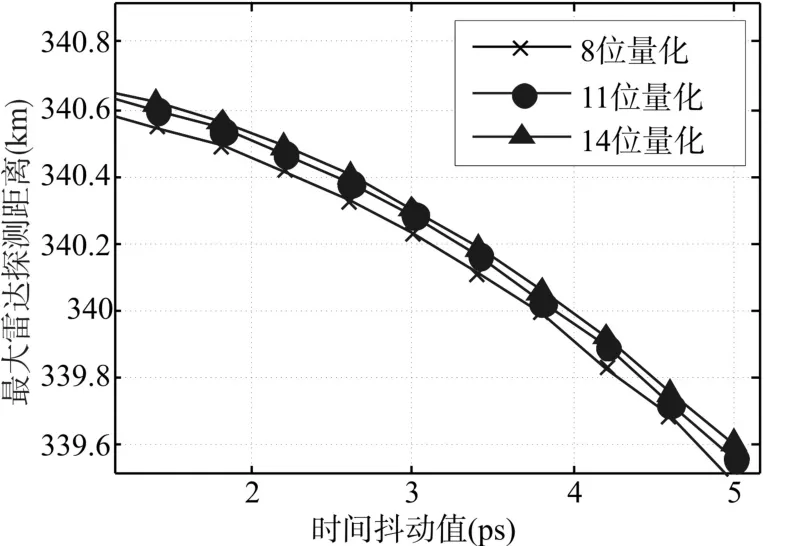
图10 不同量化误差下的雷达探测距离随时钟抖动的变化

由图10可以看出，随着时间抖动的增大，雷达的最大探测距离不断减小，并且随着ADC的位数的增大，雷达的最大探距离也在增大，但是位数对最大探测距离的影响较小。

5 结语

本文从理论上研究了ADC的采样量化以及采样时钟抖动引起的信号误差对信号信噪比和有效带宽的影响。分别对单频信号和Chirp信号进行了仿真分析。并由AD采样引起的雷达的测距理论误差进行了分析。在最后一节中，如何由ADC的动态范围的雷达性能的影响进行了讨论。

通过上述仿真研究，可以发现雷达信号处理与ADC性能直接相关。综上所述，ADC的采样率决定了雷达信号的最大带宽。同时，ADC的精度包括位和时间抖动误差不仅影响信号检测和雷达系统的性能，但也与给定的发射功率和天线增益的雷达探测范围。我们还发现，ADC的时间抖动对雷达最大探测距离有较大的影响。信号仿真结果与理论分析一致。

［1］Garenaux K，Merlet T，Alouini M，et al.Recent breakthroughs in RF photonics for radar systems［J］.IEEE Aerospace and Electronic Systems Magazine，2007，22（2）：3-8.

［2］王和国.高速高精度ADC的理论和实现［D］.西安：西安电子科技大学，2009：23-34.

［3］杨文波，陈祝明，朱晓章.时钟抖动对AD有效位数的影响［J］.电子科技大学学报，2008（s1）：3-6.

［4］方霞芳，杨文华.高速高精度AD变换器在雷达跟踪系统中的应用［J］.上海航天，2001，18（4）：38-41.

［5］Janssen E，Doris K，Zanikopoulos A，et al.An 11b 3.6 GS∕s time-interleaved SAR ADC in 65nm CMOS［C］∕∕2013 IEEE International Solid-State Circuits Conference Digest of Technical Papers.IEEE，2013：464-465.

［6］李辉，方天翔，姜俊.软件无线电在雷达信号处理中的应用［J］.战术导弹技术，2006（1）：92-96.

［7］张建志，张丽娜.带通采样时钟沿抖动对解调性能的影响分析［J］.无线电工程，2012，42（10）：10-12.

［8］高峰.跟踪雷达测距算法研究［D］.成都：电子科技大学，2013：21-32.

［9］Garmatyuk D，Schuerger J，Kauffman K.Multifunctional software-defined radar sensor and data communication system［J］.IEEE Sensors Journal，2011，11（1） ：99-106.

［10］Costanzo S，Spadafora F，Borgia A，et al.High resolution software defined radar system for target detection［J］.Journal of Electrical and Computer Engineering，2013：7.

［11］Anderson C R，Venkatesh S，Ibrahim J E，et al.Analysis and implementation of a time-interleaved ADC array for a software-defined UWB receiver［J］.IEEE transactions on vehicular technology， 2009， 58 （8） ：4046-4063.

［12］Rapuano S，Daponte P，Balestrieri E，et al.ADC parameters and characteristics［J］.IEEE instrumentationamp;measurement magazine，2005，8（5）：44-54.

［13］World Marine Radar Manual，National Defense Industry Peress，pp.229-230

［14］张志强，阮黎婷，倪涛，等.ADC模数转换器有效位计算［J］. 电子科技，2010，23（3）：84-85.

［15］LeRoy M R，Raman S，Chu M，et al.High-Speed Reconfigurable Circuits for Multirate Systems in SiGe HBT Technology［J］.Proceedings of the IEEE，2015，103（7）：1181-1196.

Analysis of the Influence of ADC Performance on Radar System

REN Shengjun CHEN Shaochang
（Electronic Engineering Institute，Naval University of Engineering，Wuhan 430033）

In the process of realizing software-based radar，digital-to-analog converter plays an important role.It is the only bridge connecting analog world and digital world.It is a vital step of radar signal entering digital processing.Therefore，the performance of ADC will have a direct impact on radar signal processing，the process of detection and estimation，and play an important role in software radar implementation.This paper analyzes and evaluates the effect of the speed and accuracy of the digital-to-analog converter on the subsequent radar signal processing.Data simulation using Matlab software to simulate ADC sampling，quantization process in a series of performance indicators，Focusing on the analysis of the impact of digital-to-analog conversion in the process of quantization noise and clock jitter on radar systems，including the impact on the signal to noise ratio，the impact of the range of the power of radar.Finally，the correctness of the theory is verified by simulation analysis.

ADC，quantization noise，clock jitter，software-based radar

TN95

10.3969∕j.issn.1672-9730.2017.10.014

Class Number TN95

2017年4月7日，

2017年5月28日

任圣君，男，硕士研究生，研究方向：电路与系统的电磁兼容性研究。陈少昌，男，教授，研究方向：电路与系统的电磁兼容性研究。