共享单车管理方案的研究

高晓红 宁静格 姚燕 陈兴 牟川林 周琪琳

三峡大学理学院

共享单车管理方案的研究

高晓红 宁静格 姚燕 陈兴 牟川林 周琪琳

三峡大学理学院

本文解决的是共享单车停放是否固定对居民生活的影响以及共享单车维修点的选取问题，针对相关问题我们建立了基于加权理想点法的综合评价模型和最优选址模型，对共享单车是否建立固定停放点进行了综合评价、选取了最优共享单车停车点。

赋值理想点法 熵权法 最小二乘法 遗传算法 综合评价模型

一、问题重述

（一）问题背景

2016年，随着OFO、摩拜等共享单车的兴起与巨大的成功，共享经济的发展模式受到了整个社会的广泛关注，共享单车得到了快速的发展。作为解决最后一公里的共享单车，其无桩式的设计，以及互联网和智能移动设备的运用，解决了以政府为主导的公共自行车的不便之处，使得自行车的寻找、使用、停放实现了随用随取、随停随放，真正体现了自行车的便利性。

（二）需要解决的问题

随着共享单车进入我们的生活，产生了诸多方面的影响，其中有正面的也有反面的，本文的意义就在于收集大量数据，探求一个合理的评价指标，分析是否固定共享单车的停放位置以及共享单车对社会经济效益的影响。

二、模型假设和符号说明

（一）模型假设

假设一：共享单车公司投放的共享单车不出现丢失情况；

假设二：共享单车在某个地区的总量保持不变，只是位置发生变化；

（二）符号说明

ta0：路段a在自由流条件下所需的行程时间

三、问题分析

首先设定多个与共享单车是否固定有关的评价指标，评价指标要与实际相结合，再根据各个评价指标对共享单车固定的影响程度大小和居民生活的贴近程度选择最佳的评价指标，根据此评价指标利用遗传算法计算共享单车固定前后与理想点的距离，根据此距离最终选择是否固定共享单车停放位置。

四、问题求解

（一）数据的去量纲化

求解步骤如下：

①假设Tn为优化目标函数，Un(Tn)为效用函数；②标记影响评价指标的关键点并确定值域内的点是否都是实际可取的，从而保证优化目标和效用函数的可比较性与效用函数的灵敏程度；③整理标记点并提供给决策者，用Bipolar尺度对每一个点的指标进行评分；④在一一对应的数组的基础上运用回归分析得到评价指标的效用函数。

运用SPSS17进行效用函数的拟合

运用SPSS进行回归分析，拟合后图像如下：

图1：运用SPSS进行回归分析的各个

指标拟合函数曲线

（1）选取R2=0.997的三次拟合曲线，得到扩展道路网络通行效率（平均阻抗）的效用函数为：

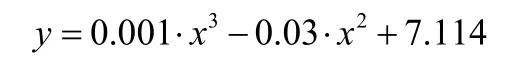
（2）选取R2=0.989的三次拟合曲线，得到安全隐患的效用函数为：

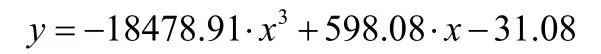
（二）综合评价模型的建立

假设求解出的理想点分别为(x1,y1,z1,g1)，即可通过比较共享单车位置固定前与固定后距离理想点的距离进行对周边道路影响的判断。

固定共享单车停车点前4个指标距离理想点的距离为：

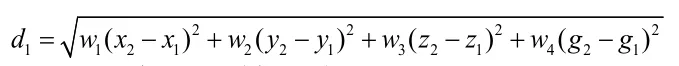
固定共享单车停车点后距离理想点的距离为：

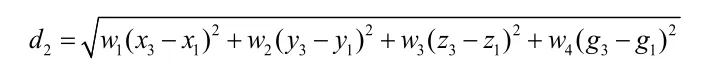
即可通过比较d1,d2的相对大小，来判断共享单车前后对周边道路的相对影响

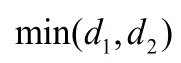
（三）模型的求解

对问题一建立的模型和综合评价指标，通过神经网络算法进行求解可以得出共享单车是否固定综合评价：

道路平均阻抗：固定前2.48，理想点3.81，固定后3.56；校容美观程度：固定前1.58，理想点2.97，固定后2.0；安全隐患：固定前2.51，理想点0.10，固定后0.15；用户满意度：固定前3.35，理想点5.27，固定后5.20；由所建立的综合评价模型中的公式可得：

共享单车位置固定后与理想点的距离为0.4849，固定前与理想点的距离为1.7030，因为距离理想点越近各个指标之间的协同程度越好，又因为固定后比固定前与理想点的距离小，所以选择固定共享单车的停放位置。

五、模型评价

（1）根据理论选择评价指标，并依据现实情况筛选出符合实际的最优评价指标，使结果更能反映出共享单车停车固定前后的影响。

（2）选择的评价指标相对较多，可以从各方面、不同程度的反映出共享单车位置的固定对周边道路通行的影响。

（3）效用函数没有确定的单位，所以在各个领域的使用都无限制，利用效用理论计算评价指标，充分发挥了效用函数理论的优势。

[1]李琨浩.基于共享经济视角下城市共享单车发展对策研究[J]. 城市,2017,(03)：66-69.

[2]李敏莲. 共享单车市场调研与分析[J]. 财经界(学术版),2017,(05)：121-123.