巧用勾股定理解决问题

朱华庆

巧用勾股定理解决问题

朱华庆

对于勾股定理,有3种常见用法：1.已知直角三角形两边，求第三边；2.已知直角三角形的两边或三边存在数量关系，可以用含同一个字母的代数式表示出来，再利用勾股定理建立方程解决问题；3.已知普通三角形三边存在某种联系，可转化为直角三角形，利用勾股定理建立方程或方程组解决问题.

一、方法回顾

对第三种较为复杂的情况，我们重点回顾一下：

例1如图1，在△ABC中，AD是BC边上的高，D为垂足，AB=15，AC=13，BC=14，求高AD.

【分析】直接用勾股定理求AD，条件不够，这里刚好有两个直角三角形，可利用两次勾股定理建立方程组.

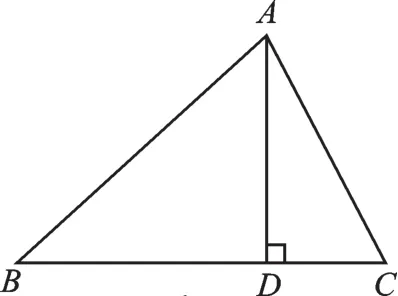
图1

【解】在Rt△ABD中，

AD2=AB2-DB2，在Rt△ACD中，AD2=AC2-CD2，则AB2-DB2=AC2-CD2，设 BD=x，CD=14-x，代入得：152-x2=132-（14-x）2.解得：x=9，代入 AD2=AB2-DB2，得AD=12.

【点评】此题是两次利用勾股定理建立方程组解决问题的典型例子.有个细节应该注意，AD虽然是两个直角三角形的公共直角边，但是直接设AD=x，计算就有很大困难，所以设未知量的时候要注意，不一定是要求什么就设什么.

二、小试牛刀

例2 如图2，在△ABC中，AE是BC边上的中线，AB=15，AC=13，BC=14，求中线AE的长.

【分析】我们应该找到以AE为边的直角三角形，如果没有，我们可以构建，这就需要作辅助线，基本上都是作垂线.

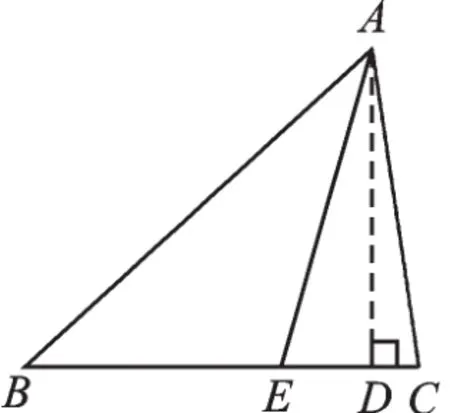
图2

【解】作AD⊥BC，垂足为D，有了例1的回顾，易求得BD=9，AD=12，由AE为中线可知，BE=7，∴ED=2，在 Rt△AED中，AE2=

【点评】在复杂问题中，如果没有合适的直角三角形，要尝试把非直角三角形转化为直角三角形来解决问题，即几何问题中“化斜为直”的思想.但要考虑好从哪个点开始作垂线，不同的作法，会导致解法的难易程度不同.

三、灵活应用

例3 如图3，某沿海城市A接到超强台风警报，在该市正南方向150km的B处有一超强台风中心正以30km/h的速度沿BC方向移动，已知城市A到BC的距离AD=90km.若在距超强台风中心的圆形区域内都受到台风的影响，问城市A是否会受到台风的影响，影响的时间有多久？（

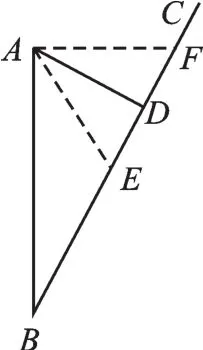
图3

【分析】只要探究台风中心距离城市A最近的情形即可.找到台风中心从开始到结束对城市A产生影响的两个位置，作出草图，利用勾股定理解决问题.

【解】当台风中心到达D处时，台风中心距离城市A最近，城市A距离台风中心，∴城市A肯定会受到台风的影响.当时，城市A刚好开始受到影响，当时，城市A刚好结束影响.在Rt△ADE中，ED2=AE2-AD2，所以DE=，所以EF=2DE=135，故t=135÷30=4.5h.

【点评】本题难点在于作图，找到台风中心对城市A开始影响和结束影响的位置.方法上与例2相同.

四、再攀高峰

例4 如图4，某沿海城市A正南方向150km处有一小岛B，有一艘旅游船以20km/h的速度从小岛出发，沿BC方向航行.已知城市A到航线BC的距离AD=90km.一艘巡逻船从城市A出发，以akm/h的速度沿直线去追赶旅游船（两船相遇以前都不停留）.（1）当a=15时，巡逻船能否追上旅游船，若能，则要几小时追上？（2）当a=20时，巡逻船能否追上旅游船，若能，则要几小时追上？

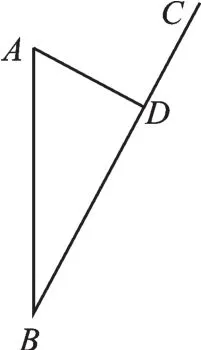
图4

【分析】当巡逻船走完最短距离AD，到达点D时，看看旅游船是否到达点D，如果没有到达，则巡逻船改变航行方向，一定可以追上旅游船，反之，则巡逻船不一定能追上旅游船.所以先判断相遇位置，再画出草图，是解决这类问题的关键.

【解】（1）在Rt△ABD中，BD2=AB2-AD2，代入得BD=120，t巡逻船=AD÷15=6，t旅游船=BD÷20=6，∴巡逻船6小时能够追上旅游船.（2）如图5，t巡逻船=AD÷20=4.5，t旅游船=BD÷20=6，所以巡逻船一定可以追上旅游船，假设巡逻船经过x小时在E处追上旅游船，则BE=20x，AE=20x，DE=120-20x，在Rt△AED中，ED2=AE2-AD2，代入得小时后，巡逻船追上旅游船.

【点评】对于这类问题，先判断能否一定追上，如果能，那么相遇点E一定在线段BD上，否则，相遇点也有可能在BD的延长线上，很容易就作出草图，然后利用勾股定理解决问题.最后，再次强调AD这条高，在复杂问题中没有给出，可以尝试作出.

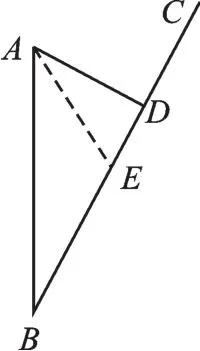
图5

五、终极挑战

例5 （2008·常州）如图6，港口B位于港口O正西方向120海里外，小岛C位于港口O北偏西60°的方向.一艘科学考察船从港口O出发，沿北偏东30°的OA方向以20海里/小时的速度驶离港口O.同时一艘快艇从港口B出发，沿北偏东30°的方向以60海里/小时的速度驶向小岛C，在小岛C用1小时装补给物资后，立即按原来的速度给考察船送去.（1）快艇从港口B到小岛C需要多少时间？（2）快艇从小岛C出发后最少需要多少时间才能和考察船相遇？

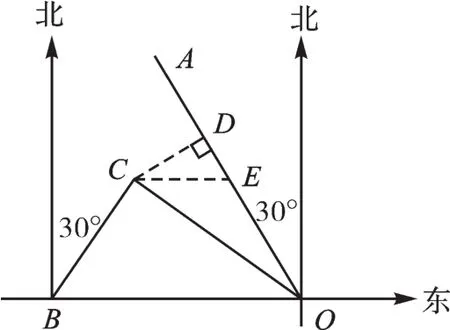
图6

【解析】题（2）当年得分率非常低，同学们利用刚才所学方法可轻松列出方程，如果方程不会解，没关系，那就到初三再解出来，正所谓“革命尚未成功,同志仍需努力”.关键是作CD⊥OA，再进行计算和判断（快艇到达点D小于1小时，而科学考察船到达点D需2.5小时），所以两船相遇点E在线段OD上，画出草图，设x小时快艇追上科考船，在Rt△CDE中用勾股定理列出方程，解决问题.参考答案：（1）t=1，（2）t=1.

（作者单位：江苏省常州市金坛区尧塘中学）