中国剩余定理和拉格朗日插值公式的关系探究

张启新

(华南师范大学 数学科学学院, 广东 广州 510631)

中国剩余定理和拉格朗日插值公式的关系探究

张启新

(华南师范大学 数学科学学院, 广东 广州 510631)

本文将中国剩余定理推广到多项式环上, 并用其推导出了拉格朗日插值公式, 以此说明拉格朗日插值公式是中国剩余定理的一个推论.

同余; 中国剩余定理; 拉格朗日插值公式

一、定义与引理

定义1 数环R上的三个多项式m(x),f(x),g(x)若满足m(x)|f(x)-g(x), 就称f(x)在模m(x)下与g(x)同余, 记作

f(x)≡g(x)(modm(x)).

比如x2+x+1≡x(modx2+1).

易知多项式环上的同余与整数的同余拥有相同的性质.

定义2 对任意a(x)∈R[x], 如果存在b(x)∈R[x]满足

a(x)b(x)≡1(modm(x))，

而且∂°(b(x))<∂°(m(x)), 那么称b(x)为模m(x)意义下a(x)的逆. 记作

b(x)=a-1(x)(modm(x)).

这里∂°(a(x))表示多项式a(x)最高次项的次数. 与整数环的情况相同, 逆存在的一个充分必要条件是原多项式和模多项式互素, 并且若逆存在, 其必是唯一的.

引理1 (余数定理)若f(x)=(x-a)q(x)+r, 则下面两个叙述等价:

(ⅰ)r=f(a)，

(ⅱ)f(x)≡r(modx-a).

证明略.

二、主要结论

类似于整数环上的中国剩余定理, 首先有

定理1 (中国剩余定理)若数环R上的n个非零次多项式m1(x),m2(x),m3(x)是两两互素的, 则方程组

有通解

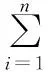
(1)

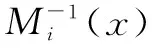
仿照整数环上的中国剩余定理的证明, 易证(1)式确是方程组的解. 在规定了解的次数后, 若存在另外的f1(x)满足上面的方程组, 且∂°(f1(x))<∂°(M(x))，那么会有

mi(x)|f(x)-f1(x),i=1,2,3,…,n.

各项相乘得

M(x)|f(x)-f1(x).

然而∂°(f(x)-f1(x))<∂°(M(x)), 所以只有f(x)-f1(x)=0, 即

f(x)=f1(x).

证毕.

下面由定理1来推导定理2.

定理2 (拉格朗日插值公式)设R上的多项式f(x)满足

f(ai)=bi,i=1,2,3,…,n+1,

(2)

其中所有ai互不相等, 且∂°(f(x))≤n, 则

证明由引理1, 条件(2)可以转变为

f(x)≡bi(modx-ai),i=1,2,3,…,n+1.

由于所有ai两两不相等, 所以所有的一次多项式x-ai是两两互素的.

由定理1,f(x)有通解

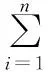
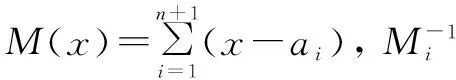
再次利用引理1, 有

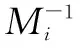
注意到∂°(f(x))≤n<∂°(M(x)), 所以f(x)是唯一确定的, 即

证毕.

我们得到结论: 拉格朗日插值公式是中国剩余定理的一个直接推论, 或者说是中国剩余定理的一种特殊形式.

[1]裴定一, 徐祥. 信息安全数学基础[M]. 北京:人民邮电出版社, 2007:17-18.

[2]孙智伟. 基础数论入门[M]. 哈尔滨:哈尔滨工业大学出版社, 2014:51-52.

[责任编辑：杨惠民]

G632

A

1008-0333(2017)27-0024-02

2017-07-01

张启新(1996.3-)，男，汉，广东省广州人，大学在读.