有源配电网中储能双层精细优化配置方法

余 涛, 袁 简， 晏 阳， 赵清源

(1. 国网江苏省电力公司常州供电公司, 江苏 常州 213003；2. 中国能源建设集团江苏省电力设计院有限公司，江苏 南京 211102)

有源配电网中储能双层精细优化配置方法

余 涛1, 袁 简2， 晏 阳2， 赵清源1

(1. 国网江苏省电力公司常州供电公司, 江苏 常州 213003；2. 中国能源建设集团江苏省电力设计院有限公司，江苏 南京 211102)

提出了一种储能的双层精细优化配置方法，结合运行与规划两个维度，实现储能容量和位置的精细配置；建立了双层规划模型，提出了对应求解方法，优化求解得到精细配置结果。精细配置模型以有源配电网成本收益为目标，针对不同的储能投资运营主体，制定了不同的成本收益模型，形成差异化目标优化配置。针对高渗透率分布式电源接入的配电网，提出的储能精细配置方法能够解决配电网电压合格率低、可再生资源浪费等问题，从而有效提高配电网可靠性和电能质量。

有源配电网; 储能配置; 精细优化; 双层模型；差异化目标

0 引言

随着清洁能源的推广和发展，具有间歇性、波动性特征的可再生能源在配电网中所占比例越来越高，带来了一系列不确定因素，影响了配电网的可靠性和电能质量。经探索，合理配置储能是目前最有效的解决方案之一，不仅能平抑可再生能源的波动特性，还能在配电网中实现能源缓存、再分配等多种功能。

储能在电力系统中的应用按功能分为三大类[1]：电网应用[2-4]、新能源应用[5-9]和用户侧应用[10，11]。文献[3]以配电网中蓄电池储能全寿命周期内总的净收益最大为目标，综合考虑了减少电能转运成本、政府电价补贴收益、储能套利收益、延缓电网升级收益及全寿命周期成本等因素，建立蓄电池储能系统配置的混合优化模型。文献[10]建立了主动配电网中储能的多目标优化配置模型，考虑电压质量、功率主动调节和削峰填谷能力3个目标，并使用带权极小模理想点法求解了该配置模型。可以看到，储能的配置研究方向正在从单点向多点、从单一功能向多功能[12-15]兼容过渡。然而，就目前储能产业的状况来看，仍有许多问题有待解决。

文章针对含高渗透率分布式电源的配电网，从两类业主角度出发，提出一种平衡功能和经济效益的储能精细配置方法。文章分为双层优化配置模型、双层模型求解方法和算例分析3个主要章节展开讨论。

1 储能双层优化配置模型

1.1 运行与规划相结合的储能配置模型

研究表明，储能的规划问题与运行策略相互影响，规划若脱离运行，会造成投资成本过高，储能设备利用率低的问题。而规划与运行时间尺度不同，混合考虑将导致建模和求解规模庞大、逻辑复杂。文章考虑将规划问题和运行问题分层优化，形成结构清晰、易于求解的双层优化模型。

外层模型为规划设计模型，以年为单位，内层模型则为运行控制模型，以天/小时/分钟为单位。如图1所示，外层模型的决策变量为安装位置X、安装额定功率S、容量E，目标函数为总投资费用fp最低；内层决策变量为影响运行控制的变量，目标为运行经济性fc，内层模型考虑所有特征运行场景，每个场景含m个运行点(LFn1～LFnm)。内外层模型通过变量X，S，E关联，求解结果满足投资成本最低、运行收益最高以及运行约束。

图1 储能优化配置双层模型示意Fig. 1 Double- layer model of Energy storage optimization configuration

1.2 规划设计层模型

规划设计层模型变量为储能的位置、额定容量、额定充/放电功率，目标为规划范围内储能的投资成本最低，约束为储能安装约束。

1.2.1 决策变量

1.2.2 目标函数

(1)

式中:cS，cE分别表示单位充/放电功率和单位容量成本。

1.2.3 约束条件

安装位置限定：

xes∈Xcap

(2)

额定容量上下限：

(3)

(4)

安装总容量限额：

(5)

(6)

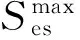
1.3 运行控制层模型

运行控制层用于对具体运行过程建模，该层反映出储能运行策略和配电网控制要求，由此计算出运行各阶段的经济成本和收益。因此，制定运行控制层的目标为运行总收益最大，变量为运行点状态变量。

1.3.1 决策变量

决策变量设计如表1所示，包含节点/支路、场景、运行点3个维度。表中：i表示网络节点；ij表示支路；Sc表示模拟场景；T表示总运行点数；t表示运行点。

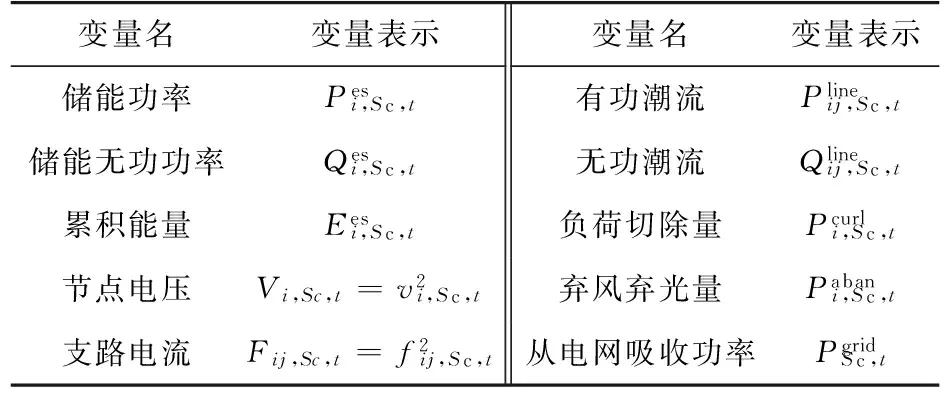
表1 决策变量Table 1 Decision variable table

1.3.2 目标函数

F(Pes,Qes,V,F,Pline,Qline,Pgrid,Pcurl,Paban)=minfc

(7)

式中：fc为成本收益函数。

此处分别针对两类业主建立2种成本收益函数。一类业主指有投资和运营可再生电源能力的公司，通过投资储能获取运行服务收益；二类业主是售电公司，其投资目的是延缓电网升级，获取运行收益及其他间接收益。

(1) 一类业主经济目标函数。

① 年运行维护成本[8]：

(8)

② 储能售电收益：

(9)

③ 储能辅助服务收益，表示储能在未满发时备用容量可提供辅助服务，即：

(10)

综上，针对一类业主的目标函数表示为：

fc=w1f1-w2f2-w3f3

(11)

式中：wi为各部分成本/收益的权重系数，通过层次分析法获得。

(2) 二类业主经济目标函数。

① 运行维护成本与一类业主相同。

② 从上级电网购电成本：

(12)

③ 向上级电网售电收益：

(13)

④ 网络损耗减小收益：

(14)

⑤ 停电损失减小收益，将减少用户停电次数和频率折算为收益：

(15)

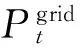
综上，针对二类业主的成本收益函数为：

fc=w1f1+w4f4-w5f5-w6f6-w7f7

(16)

1.3.3 约束条件

(1) 储能运行约束：

(17)

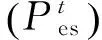
(18)

Ees(t+1)=Ees(t)+Pes(t+1)·1

(19)

(20)

式(19)中：Emin表示储能最小剩余容量的比值。

式(17)和式(18)[9]为储能运行功率限制，式(19)和式(20)为储能运行时的能量限制。

(2) 电网安全约束：

(21)

(22)

(23)

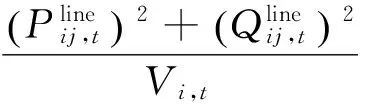
(24)

Vmin≤Vt≤Vmax

(25)

Fmin≤Ft≤Fmax

(26)

其中，式(21—24)为潮流方程约束，式(25，26)为节点电压、线路潮流幅值约束。

(3) 其他约束：

0≤Pcur≤λPD

(27)

0≤Paban≤θPdg

(28)

式中：λ和θ分别为负荷可切除量和可再生能源可舍弃量比值。式(27，28)分别为负荷可切除量和可再生能源可舍弃量约束。

1.3.4 分布式电源和负荷数据处理

分布式电源与负荷的数据采用聚类法，将历史数据聚类为有限个特征场景(Sc)带入计算。

2 双层模型求解方法

双层模型的外层是一个典型的组合优化问题，内层为最优潮流问题，拟采用启发式算法与求解器混合的方法来求解，平衡计算精度与计算速度。

2.1 内层模型求解方法

内层模型求解采用MATLAB-YALMIP工具进行模型的建立，调用GUROBI求解器[16]求解。

2.2 外层模型求解方法

外层规划模型采用模拟退火法，是局部搜索算法的扩展，可在多项式时间里给出近似最优解。

基本计算过程是：(1) 任选一个初始解x0；xi=x0；k=0；t0=tmax。(2) 若在该温度达到内循环条件，则到第(3)步；否则从邻域N(xi)中随机选一xj，计算Δfij=f(xj)-f(xi)，若Δfij≤0，则xi=xj；否则根据Metropolis准则，若e-Δfij/tk>random(0,1)时，则xi=xj；重复这一步。(3)tk+1=d(tk)；k=k+1；若满足停止条件，终止计算；否则，回到第(2)步。

模拟退火算法的退火过程用“冷却进度表”表示，包括控制参数的t的初值t0，即初始温度的选取；控制参数t的衰减函数，即温度下降的规则；马氏链的长度Lk，即每个温度马氏链的迭代长度；控制参数t的终值tf，即终止准则。最终，由GUROBI求解器和模拟退火算法组成的双层优化配置模型求解方法，其流程如图2所示。

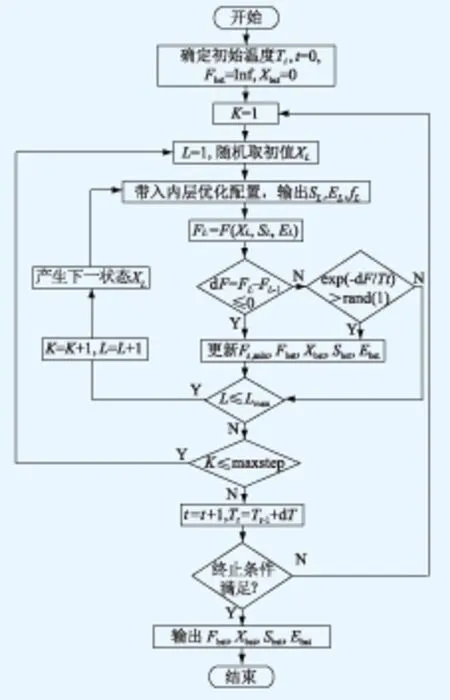
图2 储能系统优化配置模型求解流程Fig.2 Solving flow chart of energy storage system optimization configuration model

3 算例分析

3.1 算例

配置方法的验证系统采用IEEE 33节点配电系统，如图3所示。随机接入适当容量的分布式电源，作为含分布式电源的配电网系统，验证提出的储能配置方法。从分布式电源渗透率、储能配置数量和储能投资方三个维度划分算例场景，如表2所示。利用文中的优化配置方法对算例进行计算分析。

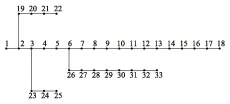
图3 33节点配电系统网络结构Fig.3 33 node distribution network system network structure diagram

场景划分渗透率/%配置数量投资方1501一类业主2501二类业主3505一类业主4505二类业主51001一类业主61001二类业主71005一类业主81005二类业主

3.2 配置结果分析

8个场景的储能优化配置结果如表3所示。结果表明，储能主要配置在线路末端，容量随分布式电源增加而增加，在有限的配置数量要求下，对分布式电源发出的电能实现了时间和空间上的迁移。

从配置位置和容量来看，配置集中式单个储能时，储能最优位置在线路末端；

配置分散式多个储能时，储能在接入分布式电源的线路上均匀分布，安装总容量低于集中配置容量。分布式电源渗透率越高，分散配置比集中配置的安装容量减少越多。因此，储能小容量分散配置效率更高。

从成本收益看，对一类业主，大部分收益来源于辅助服务，且集中配置时更高，说明集中式储能的容量利用率并不高，但能提供更多辅助业务，因此可根据不同场景选择不同的配置方式。

对二类业主，储能分散配置容量大于集中配置容量，而分散收益却明显较高，原因是其获利渠道更多，长期运营累积收益更高。因而，若只考虑一次性投资成本，建议配置集中式储能；若考虑运营收益则建议投入分散式储能。

从表3中还可看出，配电网从上级电网的购电成本接近或等于零，说明通过储能对分布式电源出力在时间和空间上进行了迁移，已经能够很好地为本地负荷服务，从而减少配电网从上级电网的购电量，并将余电传输至上级电网。

表3 储能优化配置结果Table 3 Energy storage optimization configuration results

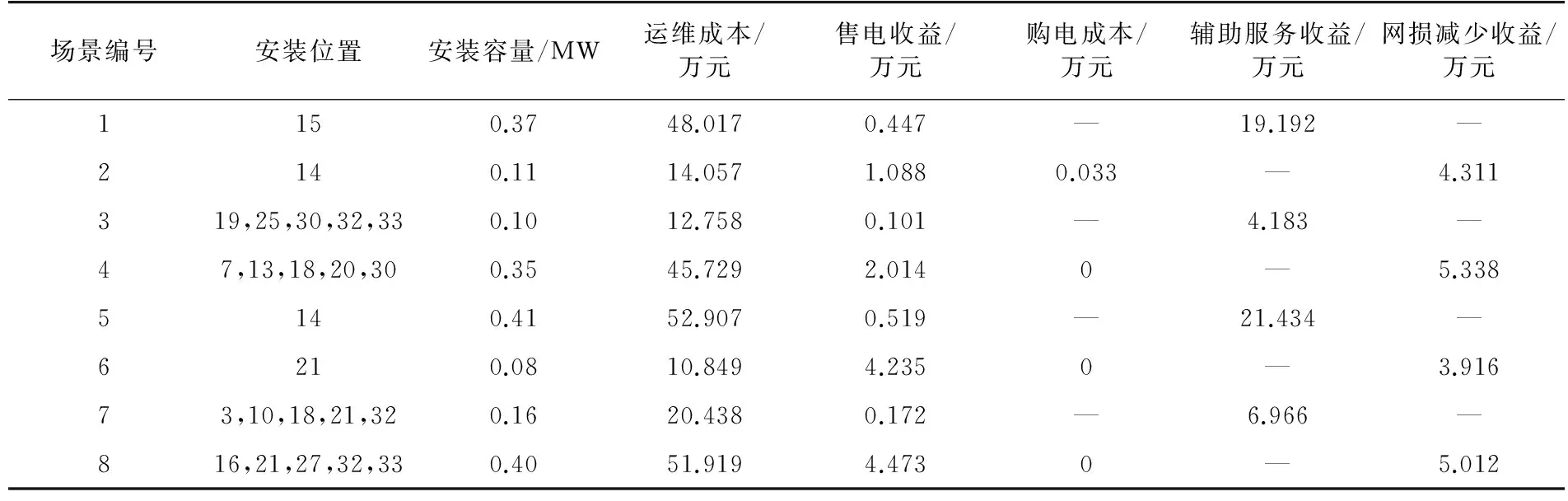
场景编号安装位置安装容量/MW运维成本/万元售电收益/万元购电成本/万元辅助服务收益/万元网损减少收益/万元1150.3748.0170.447—19.192—2140.1114.0571.0880.033—4.311319,25,30,32,330.1012.7580.101—4.183—47,13,18,20,300.3545.7292.0140—5.3385140.4152.9070.519—21.434—6210.0810.8494.2350—3.91673,10,18,21,320.1620.4380.172—6.966—816,21,27,32,330.4051.9194.4730—5.012

3.3 运行结果分析

运行结果采用分布式电源渗透率50%时，投资运营方为二类业主的场景为例进行分析。图4和图5分别表示某天充放电功率和系统能量曲线。图4中Pes为正表示充电，为负表示放电。可以看出储能的充放电规律，一天中00:00—07:00时和19:00—24:00时为储能的充电时段，通过分布式电源或上级电网充电，此时负荷较小，且能保证配电网白天的供电质量。在图5中也有所体现。08:00—18:00时为一天中负荷的用电高峰，储能基本处于放电状态，充电或不充不放的情况表示分布式电源发电功率较大，能够完全满足负荷需求。运行数据说明，储能设备的利用率较高，无长期闲置或过度充放电情况，也证明通过文中优化方法得到的储能容量符合运行需求。

图4 渗透率为50%时的储能充放电功率曲线Fig.4 Energy storage and discharge power curve when the penetration rate is 50%

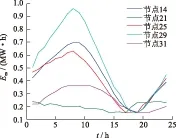
图5 渗透率为50%时的储能能量曲线Fig.5 Energy storage energy curve when the penetration rate is 50%

图6为某时刻投入储能前后的节点电压曲线，可以看出，储能的投入将被分布式电源抬高的电压拉回正常范围内，提高了电压合格率。

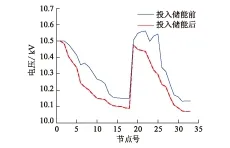
图6 某时刻投入储能前后节点电压曲线Fig. 6 The voltage curve of the node before and after the energy storage

4 结论

针对分布式电源对配电网的诸多影响，结合运行控制与规划设计两个不同时间尺度的优化配置储能方法，建立了包含运行和规划两个层面的精细优化配置模型，对两类投资主体分别建立了经济目标模型。同时采用模拟退火算法和商业求解器相结合的双层求解方法求解模型，保留了模型的双层特征，兼顾了精度与时间的要求，适合于大规模混合整数双层优化模型的计算。结论如下：(1) 储能分散配置较集中配置效率优、投资省；(2) 随着分布式电源渗透率增加，储能的配置容量并未同等增加，说明储能的一次投资可以应对远景分布式电源的增加；(3) 储能的运行策略可以保证储能充放有度，延长寿命。

[1] 王承民，孙伟卿，衣 涛，等. 智能电网中储能技术应用规划及其效益评估方法综述[J]. 中国电机工程学报，2013(7): 33-41.

WANG Chengmin, SUN Weiqing, YI Tao, et al. Review on energy storage application planning and benefit evaluation methods in smart grid[J]. Proceedings of the CSEE, 2013(7): 33-41.

[2] 杨玉青，牛利勇，田立亭，等. 考虑负荷优化控制的区域配电网储能配置[J]. 电网技术，2015(4): 1019-1025.

YANG Yuqing, NIU Liyong, TIAN Liting, et al. Configuration of energy storage devices in regional distribution network considering optimal load control[J]. Power System Technology, 2015(4): 1019-1025.

[3] 向育鹏，卫志农，孙国强，等. 基于全寿命周期成本的配电网蓄电池储能系统的优化配置[J]. 电网技术，2015(1): 264-270.

XIANG Yupeng, WEI Zhinong, SUN Guoqiang, et al. Life cycle ost based optimal configuration of battery energy storage system in distribution network[J]. Power System Technology, 2015(1): 264-270.

[4] 黎静华，文劲宇，程时杰，等. 基于p-有效点理论的含大规模风电电力系统最小储能功率配置方法[J]. 中国电机工程学报， 2013(13): 45-52.

LI Jinghua, WEN Jinyu, CHENG Shijie, et al. Method of minimum energy storage power allocation for electric power systems with large-scale wind power based on p-efficient point theory[J]. Proceedings of the CSEE, 2013(13): 45-52.

[5] 梅生伟，王莹莹，刘 锋. 风—光—储混合电力系统的博弈论规划模型与分析[J]. 电力系统自动化，2011(20): 13-19.

MEI Shengwei, WANG Yignying, LIU Feng. A game theory based planning model and analysis for hybrid power system with wind generators-photovoltaic panels-storage batteries[J]. Automation of Electric Power Systems, 2011(20): 13-19.

[6] 王成山，于 波，肖 峻，等. 平滑可再生能源发电系统输出波动的储能系统容量优化方法[J]. 中国电机工程学报， 2012, 32(16): 1-8.

WANG Chengshan, YU Bo, XIAO Jun, et al. Sizing of energy storage systems for output smoothing of renewable energy systems[J]. Proceedings of the CSEE, 2012, 32(16): 1-8.

[7] 严干贵，冯晓东，李军徽，等. 用于松弛调峰瓶颈的储能系统容量配置方法[J]. 中国电机工程学报，2012(28): 27-35.

YAN Gangui, FENG Xiaodong, LI Junhui, et al. Optimization of energy storage systems capacity for relaxing peak load regulation bottlenecks[J]. Proceedings of the CSEE, 2012(28): 27-35.

[8] 林少伯，韩民晓，赵国鹏，等. 基于随机预测误差的分布式光伏配网储能系统容量配置方法[J]. 中国电机工程学报，2013(4): 25-33.

LIN Shaobo, HAN Minxiao, ZHAO Guopeng, et al. Capacity allocation of energy storage in distributed photovoltaic power system based on stochastic prediction error[J]. Proceedings of the CSEE, 2013(4): 25-33.

[9] 孙承晨，袁 越，San Shing Choi，等. 基于经验模态分解和神经网络的微网混合储能容量优化配置[J]. 电力系统自动化，2015(8): 19-26.

SUN Chengchen, YUAN Yue, San Shing Choi, et al. Capacity optimization of hybrid energy storage systems in Microgrid using empirical mode decomposition and neural network[J]. Automation of Electric Power Systems, 2015(8): 19-26.

[10] 尤 毅，刘 东，钟 清，等. 主动配电网储能系统的多目标优化配置[J]. 电力系统自动化，2014(18): 46-52.

YOU Yi, LIU Dong, ZHONG Qing, et al. Multi-objective optimal placement of energy storage systems in an active distributionnetwork[J]. Automation of Electric Power Systems, 2014, 38(18):46-52.

[11] 颜志敏，王承民，连鸿波，等. 计及缺电成本的用户侧蓄电池储能系统容量规划[J]. 电力系统自动化， 2012(11): 50-54.

YAN Zhimin, WANG Chengmin, LIAN Hongbo, et al. Capacity plan of battery energy storage in user side considering power outage cost[J]. Automation of Electric Power Systems, 2012(11): 50-54.

[12] 李丹丹，苏小林，阎晓霞，等. 储能优化配置关键问题分析[J]. 电力建设，2016, 37(9):70-78.

LI Dandan, SU Xiaolin, YAN Xiaoxia, et al. Principal problems of energy storage optimization allocation[J]. Electric Power Construction, 2016, 37(9):70-78.

[13] 潘文霞，徐才华. 孤岛风光柴蓄系统配置仿真及分析[J]. 江苏电机工程，2008, 27(6):34-37.

PAN Wenxia, XU Caihua. The configuration simulation and analysis of hybrid diesel-wind-solar-battery power systems on isolated islands[J]. Jiangsu Electrical Engineering, 2008, 27(6):34-37.

[14] 张国玉，洪 超，陈杜琳，等. 面向储能电站调度的光储发电系统运行优化策略研究[J]. 电力工程技术，2017, 36(3)：50-56.

ZHANG Guoyu, HONG Chao, CHEN Dulin, et al. Operation optimization of photovoltaic-energy storage hybrid system based on scheduling of battery energy storage system[J]. Electric Power Engineering Technology, 2017, 36(3)：50-56.

[15] LEOU R. An economic analysis model for the energy storage system applied to a distribution substation[J]. International Journal of Electrical Power & Energy Systems. 2012, 34(1): 132-137.

[16] Gurobi Optimization，Inc. Gurobi optimizer reference manual，version 5.6[EB/OL]. [2013-01-01]. http：∥www.gurobi.com.

余 涛

余 涛(1972—)，男，江苏常州人，高级工程师，从事电力系统及其自动化系统生产技术管理工作(E-mail：yutao@js.sgcc.com.cn)；

袁 简(1991—)，女，江苏镇江人，硕士研究生，从事配电网规划研究工作(E-mail：yuanjian@jspdi.com.cn)；

晏 阳(1988—)，男，云南宣威人，工程师，从事配电网规划研究工作(E-mail：yanyang@jspdi.com.cn)；

赵清源(1989—)，男，江苏常州人，工程师，从事电力系统及其自动化研究工作(E-mail：731596683@qq.com)。

(编辑江 林)

ATwo-layerDetailedOptimizationAllocationMethodofEnergyStorageinActiveDistributionNetwork

YU Tao1, YUAN Jian2，YAN Yang2，ZHAO Qingyuan1

(1. State Grid Changzhou Power Supply Company, Changzhou 213003, China；2. China Energy Engineering Group Jiangsu Power Design Institute，Nanjing 211102, China)

A two-layer detailed optimization method is proposed for the allocation of energy storage capacity and location, combining the distribution network operation and planning. A two-layer planning model is established and the corresponding solution method is proposed. The configuration results are obtained by optimizing the solution. The allocation model takes the cost of active distribution network as the goal. Different cost-economic models were made for different energy storage investors, realizing differentiation goal optimization allocation. As for the distribution network with high penetration of distributed power, the proposed method can solve problems of low qualified rate of distribution network voltages and waste of renewable resources. Therefore, the reliability and power quality of the distribution network can be improved effectively.

active distribution network; energy storage allocation; detailed optimization; two-layer model; differentiation goal

TM727

A

2096-3203(2017)06-0111-06

2017-06-21；

2017-07-27

国家电网公司科技项目(SGTYHT16-JS-198)；中国能源建设集团科技项目(CEEC2015-KJ05)