浅析FFT算法中对称关系

李艳凤， 陈后金， 胡 健

(北京交通大学 电子信息工程学院, 北京 100044)

浅析FFT算法中对称关系

李艳凤， 陈后金， 胡 健

(北京交通大学 电子信息工程学院, 北京 100044)

本文通过分析比较时间抽取FFT算法以及频率抽取FFT算法的基本原理，揭示了FFT算法中存在的对称关系，同时也给出了任意基FFT算法系数矩阵的产生机理。上述的分析比较有助于学生更好地理解和实现FFT算法，同时也可借鉴该算法的思想设计其他算法。

时间抽取FFT；频率抽取FFT；对称关系

0 引言

离散傅里叶变换DFT (Discrete Fourier Transform)在数字信号处理中的重要性早已被人们所认识，但其得到广泛应用却经历了较长时间，其原因在于计算量太大难以实用[1]。快速傅里叶变换FFT(Fast Fourier Transform)是各种DFT快速算法的统称，目前较为普遍使用的算法是基于Cooly和Tukey提出的FFT算法[2]。本文通过比较分析时间抽取FFT算法以及频率抽取FFT算法的基本原理，揭示了FFT算法中存在的对称关系，同时也给出了任意基FFT算法系数矩阵的产生机理。上述的比较分析充分展现了FFT算法中蕴含的对称之美，有助于学生更好地理解和实现FFT算法，也有助于任意基FFT算法的学习和掌握。

1 时间抽取FFT

(1)基2时间抽取FFT：时域上将数据按照奇偶进行逐级拆分，最终得到多组两点时域数据，通过计算两点序列的DFT将时域变换到频域，然后利用两个短序列的DFT逐级合成长序列的DFT，该合成过程称为频域合成[3]。

两点序列时域(x[0]和x[1])到频域(X[0]和X[1])的矩阵表示式为

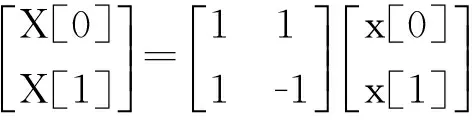
(1)

两个短序列DFT(X1[m]和X2[m])合成长序列DFT(X[m])的频域合成矩阵表示式为

(2)

式(2)中，等式右边第一个矩阵为系数矩阵，第二个矩阵为旋转因子矩阵。频域合成的蝶形图如图1所示。

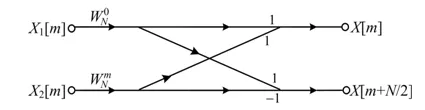
图1 基2时间抽取频域合成蝶形图

(2)基4时间抽取FFT：时域上将数据按照基4进行逐级拆分，最终得到多组四点时域数据，通过计算四点序列的DFT将时域变换到频域，然后利用四个短序列的DFT逐级合成长序列的DFT。

四点序列时域(x[0]、x[1]、x[2]和x[3])到频域(X[0]、X[1]、X[2]和X[3])的矩阵表示式为

(3)

四个短序列DFT(X1[m]、X2[m]、X3[m]和X4[m])合成长序列DFT(X[m])的频域合成矩阵表示式为

(4)

2 频率抽取FFT

(1)基2频率抽取FFT：时域上将一组长序列分解为两组短序列，经过多次分解得到多组两点时域序列，然后计算两点时域序列的DFT将时域变换到频域。

长序列时域数据(x[k])分解为两组短序列时域数据(x1[k]和x2[k])的矩阵表示如式(5)所示，时域分解的蝶形图如图2所示。

(5)

图2 基2频率抽取时域分解蝶形图

两点序列时域到频域的计算与基2时间抽取FFT中时域到频域计算相同，得到X1[m]和X2[m]。短序列DFT与长序列DFT的关系为：X[2m]=X1[m]，X[2m+1]=X2[m]。

(2)基4频率抽取FFT：时域上将一组长序列分解为四组短序列，经过多次分解得到多组四点时域序列，然后计算四点时域序列的DFT将时域变换到频域。

长序列时域数据(x[k])分解为四组短序列时域数据(x1[k]、x2[k]、x3[k]和x4[k])的矩阵表示式为

(6)

四点序列时域到频域的计算与基4时间抽取FFT中时域到频域计算相同，得到X1[m]、X2[m]、X3[m]和X4[m]。短序列DFT与长序列DFT的关系为：X[4m]=X1[m]，X[4m+1]=X2[m]，X[4m+2]=X3[m]，X[4m+3]=X4[m]。

3 对称性分析

对上述FFT算法进行分析，可以看到FFT算法蕴含的对称关系。

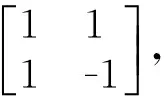
4 系数矩阵的机理

基2时间或频率抽取FFT算法的系数矩阵可用单位圆二等分(如图3(a)所示)生成。W2m的值为单位圆二等分的值，系数矩阵的每行都是以W20为起点顺时针等间隔采两个点，第一行间隔W20，第二行间隔W21，如图3(b)所示。

基4时间或频率抽取FFT算法的系数矩阵可用单位圆四等分(如图4(a)所示)生成。W4m的值为单位圆四等分的值，系数矩阵的每行都是以W40为起点顺时针等间隔采四个点，第一行间隔W40，第二行间隔W41，第三行间隔W42，第四行间隔W43，如图4(b)所示。

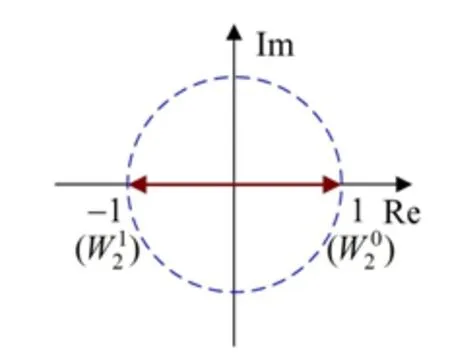
(a)单位圆表示

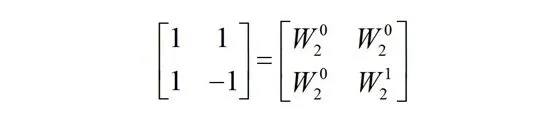
(b)系数矩阵图3 基2抽取FFT算法中系数矩阵的生成

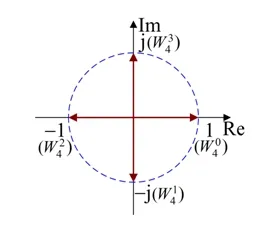
(a) 单位圆表示

(b) 系数矩阵图4 基4抽取FFT算法中系数矩阵的生成

可以证明，对于基r抽取FFT算法，其系数矩阵也可采用单位圆r等分方法得到。如基3抽取FFT算法，其系数矩阵如图5所示。

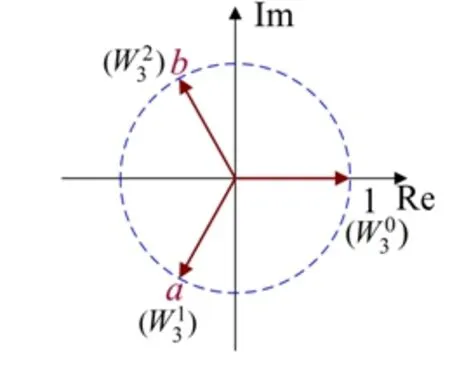
(a) 单位圆表示

(b) 系数矩阵

(李艳凤等文)

5 结语

本文给出了时间抽取FFT算法以及频率抽取FFT算法存在的对称关系，同时也给出了任意基FFT算法系数矩阵的产生机理。该分析过程有助于学生更好地理解和实现任意基FFT算法，同时也可借鉴该算法的思路设计其他算法。

[1] 陈后金, 薛健, 胡健. 数字信号处理(第二版)[M]. 北京: 高等教育出版社, 2008年11月.

[2] 吴镇扬. 数字信号处理(第二版)[M]. 北京: 高等教育出版社, 2010年4月.

[3] 陈后金, 李居朋, 姚畅, 李艳凤(译). 数字信号处理及MATLAB仿真[M]. 北京: 机械工业出版社, 2015年1月.

DiscussiononSymmetryinFFTAlgorithm

LIYan-feng，CHENHou-jin，HUJian

(SchoolofElectronicandInformationEngineering,BeijingJiaotongUniversity,Beijing100044,China)

This paper analyzes and compares the basic theory between the decimation-in-time FFT and decimation-in-frequency FFT. The symmetry in FFT algorithm is revealed. Moreover, the generation mechanism of the coefficient matrix in FFT under arbitrary base is given. The symmetry analysis can help student better understand and implement the FFT algorithm. Also, the idea of FFT can be applied when designing other algorithms.

decimation-in-time FFT; decimation-in-frequency FFT; symmetry

2017-10-11;

2017-01-03

国家级电子信息与计算机实验中心建设项目(No．274020529)

李艳凤(1988-)，女，博士，副教授，主要从事信号与信息处理以及模式识别教学与研究工作，E-mail：yf.li@bjtu.edu.cn 陈后金(1965-)，男，博士，教授，主要从事信号与信息处理教学与研究工作，E-mail：hjchen@bjtu.edu.cn 胡 健(1965-)，女，硕士，副教授，主要从事信号与系统以及数字信号处理教学工作，E-mail：jhu@bjtu.edu.cn

TN911.72

A

1008-0686(2017)05-0078-04