应用改进蚁群算法的同心分布喷丝孔检测路径规划
郭隽侠, 陶建峰, 刘成良
(上海交通大学 机械与动力工程学院, 上海 200240)
应用改进蚁群算法的同心分布喷丝孔检测路径规划
郭隽侠, 陶建峰, 刘成良
(上海交通大学 机械与动力工程学院, 上海 200240)
为提高微孔同心分布喷丝板的检测效率,提出一种基于改进蚁群算法的微孔检测路径规划方法。该方法针对传统蚁群算法收敛速度慢、易陷入局部最优等缺陷进行优化改进:重新定义微孔间的距离以适应典型喷丝板检测仪运动特点;采用最近邻法设定初始信息素浓度表,使蚁群算法在相同的迭代次数等参数下求得更优的路径结果;通过路径尖端去除处理对蚁群算法的结果进一步优化,得到了优化的微孔检测路径。为验证算法的有效性,以典型的微孔同心分布喷丝板为算例进行检测路径的规划计算。结果表明,所提出的算法具有较快的收敛速度,优化所得路径与传统逐圈检测路径相比缩短路径长度约18%,可显著提高对应喷丝板的检测效率。
喷丝板检测; 蚁群算法; 信息素浓度; 最近邻法; 最优化
喷丝板是化纤纺丝工艺中最为重要的部件,其质量在很大程度上决定了纤维质量的优劣以及纺丝能否顺利进行,因而喷丝板的质量检测是相关生产过程中必不可少的流程。喷丝板上的微孔数量多,孔径小,传统的人工检测方式普遍存在效率低、精度较差的缺陷[1]。随着工业自动化技术的不断发展,喷丝板自动检测技术越来越受到人们的重视。喷丝板自动检测仪的原理是由电动机带动镜头遍历每个微孔的正上方进行微孔图像采集,再传入计算机加以辨识。在硬件设施不变的前提下,镜头对每个微孔的遍历顺序是决定检测效率的重要因素,因此,寻找一种优化的镜头运动路径对于提高喷丝板检测速度具有重要的现实意义。
喷丝孔检测路径的设计可抽象为经典的旅行商问题(简称TSP),这是一个多项式复杂程度的非确定性问题(NP完全问题),其庞大的求解计算量使得精确求解难以实现。目前较为成熟的近似求解算法包括遗传算法[2]、模拟退火算法[3]、果蝇算法[4]等。蚁群算法是20世纪90年代由意大利数学家Dorigo等[5]率先提出的针对旅行商问题的求解算法,该算法受到自然界中蚂蚁通过信息素正反馈的方式寻找巢穴到食物最短路径的启示,采用加强较短路径的选择概率,达到逼近最优路径的目标。这种方法具有鲁棒性强、收敛速度易于控制、可灵活改进等优势,因而被广泛应用于飞行器路径设计[6]、军事目标打击顺序配置[7]、优化生产线中的缓冲容量配置[8]等诸多领域中。
目前,针对喷丝板微孔检测路径优化算法的研究极少,还没有关于以蚁群算法为基础规划喷丝板检测路径的文献报道。此外,传统蚁群算法存在算法时间长且易陷入局部最优的缺点,为此,近年来纷纷提出相关的改进算法。SONG等[9]改进了信息素的取值和更新方式,引入信息素上下限的概念,改善了陷入局部最优的情况但无法使收敛速度得到有效提高;GAN等[10]将人工蚂蚁的一部分分类为“侦察蚁”,减少了总运算量;YANG等[11]引入突变过程和局部搜索等概念,均对提高算法效率起到了一定的推进作用,但得到的优化结果仍有较大的改进空间。
本文研究针对喷丝板微孔检测路径缺乏合理设计导致检测效率低的现状,设计了一种基于改进蚁群算法的同心分布微孔检测路径规划方法,即在传统蚁群算法基础上重新定义微孔间的距离,采用最近邻法设定初始信息素浓度表,并通过路径尖端去除处理对蚁群算法的结果进一步优化,得到了优化的微孔检测路径。首先对于喷丝板微孔检测路径规划问题提出数学假设并建立数学模型;接着,介绍了蚁群算法的流程和重要改进点;然后,通过MatLab软件运行验证方案的可行性和收敛速度、路径长度等重要指标,与传统算法进行对比;最后,给出算法效果的评价并进行总结。
1 检测路径规划问题建模
1.1假设
图1示出典型的XY运动平台驱动的喷丝板自动检测仪。针对其检测路径规划问题,为建立相应的数学模型并确定算法适用范围,给出假设如下。
1)喷丝板上所有微孔都需被检测。
2)每个微孔只被检测1次。
3)带有检测镜头相机的X、Y两轴电动机最大运行速度相同,因而镜头从某一位置移动至另一位置的耗时取决于这2个位置中X和Y坐标差较大者。
4)喷丝板上微孔为同心圆或类同心圆形式分布。
5)电动机有足够的行程,即可装载镜头相机到达喷丝板任一微孔的正上方。
6)不考虑镜头在Z方向(竖直方向)上的移动。
7)假定电动机带动镜头从某一孔移动至另一孔的过程为匀速运动,忽略电动机的加速和减速过程。

图1 典型的喷丝板检测仪Fig.1 Typical spinneret detector
1.2数学模型
由于平面XY运动平台的特性,本文研究对于2个微孔间的距离不采用通常的欧氏距离,而由2个微孔在X、Y方向的坐标差较大值重新定义,即对于任何2个微孔Vi(xi,yi)和Vj(xj,yj),定义
dVi,Vj=max{|xi-xj|,|yi-yj|}
(1)
为微孔间距离,并由此建立目标问题的数学模型。
已知无向赋权图G=(V,E),求总权重最小的Hamilton圈。其中:V={V1,V2,…,Vn}为顶点集,表示n个微孔的集合;E={eij|i,j∈1,2,…,n}为各顶点组成的边集,表示两两微孔间连线的集合。
每条边都存在与之对应的权重dVi,Vj,表示微孔间的距离,由式(1)给出。
由于两两微孔间的距离具有对称性,因此可认为对任意的Vi、Vj,dVi,Vj=dVj,Vi。
设微孔的搜索顺序为P={P1,P2,…,Pn},Pi∈V,并规定P0与Pn+1均表示原点,则目标函数为
(2)
式(2)中dPi,Pi+1为点Pi与点Pi+1间的距离,其定义方式与式(1)相同。
这个数学模型具有易于描述但难以求解的特点,利用穷举法精确求出最优解要对所有可行路径进行逐一比较,这需要与(n-1)!/2相当的计算量级,如表1所示。这意味着当n=50时,需要约1.5×1064次运算,即使在计算机技术发展到相当高程度的当下,也是相当耗时的,这显然无法满足现实检测需求,因此,采用合理的优化算法在保证一定精度和效率的前提下求出该问题的次优解,是求解该数学模型的必然选择。

表1 不同微孔数量下的TSP穷举法计算量与耗时Tab.1 Compute and time-consuming of TSP exhaustive method under different micropore numbers
2 算法及其改进
2.1蚁群算法
蚁群算法是一种典型的求解TSP问题的概率型算法,其核心原理是建立若干代路径方案,通过合理改变后代路径规划时每个微孔前往其他微孔的概率逐渐逼近最优路径。这个概率受2个因素共同影响,即两两微孔间的距离与信息素浓度。
信息素浓度[12]是蚁群算法的重要概念,自然界中蚁群在寻找食物或寻找回巢路径过程中,会在所经过的路上释放一种化学物质,该物质浓度越高,其他蚂蚁选择其对应路径的概率就越大。对于长度较短的路径,在一定时间内通常会有更多的蚂蚁访问,因而积累的信息素浓度就越高,这种蚁群寻找最优路径中所释放的重要物质称为信息素。
图2示出蚁群信息素优化过程。如图2(a)所示为起点至终点的3条可行路径,初始状态下蚁群选择每条路径的概率相同,并沿途释放信息素。随着时间的推移,最优路径(路径2)上的信息素浓度逐渐高于另2条路径,后续的蚂蚁有更高几率选择路径2,并释放更多信息素形成正反馈,如图2(b)所示。最终,蚁群在路径2上堆积大量信息素,而另2条路径上的信息素几乎完全挥发,蚁群便得到了起点至终点的最优路径,如图2(c)所示。
人工蚁群算法的寻优过程较自然界蚁群的寻优方式进行了改进,其主要优势在于人工蚁群具有一定的记忆能力,可记忆已被访问过的节点,同时在寻找路径时也不像自然蚁群那样盲目,而是可有意识地根据一定算法规律寻找路径方案。
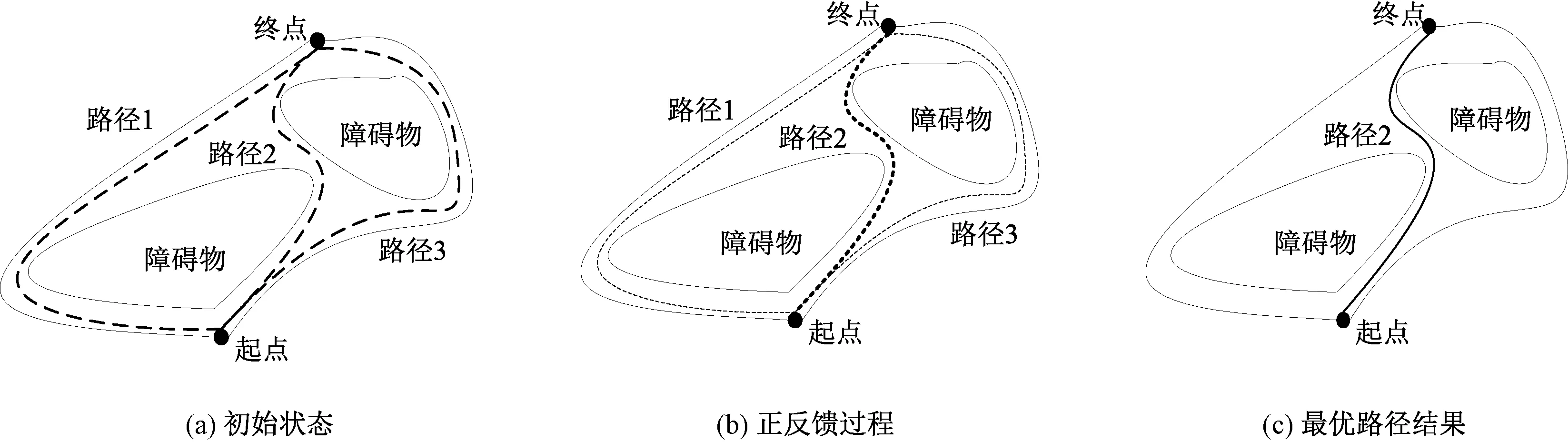
图2 蚁群信息素优化过程Fig.2 Optimization process of ant colony by pheromone. (a) Initial state; (b) Positive feedback process; (c) Optimal route result
2.2基于蚁群算法的微孔检测路径优化
就喷丝板微孔检测路径而言,设共规划k代路径方案,第k代路径规划过程中,对微孔Vi检测完毕后前往检测微孔Vj的概率pij(k)为
pij(k)=αEij(k)+βDij
(3)
式中,Eij为微孔Vi到微孔Vj中的信息素浓度,在每一代路径方案规划完毕后根据当前全局最优路径方案进行更新。迭代至第k代后的Eij(k)由式(4)得到。
(4)
式(4)中ρ称为挥发度,反映每次迭代后最优路径上的信息素浓度相对于其他路径上信息素浓度的增加程度。
式(3)中,Dij表示微孔Vi(xi,yi)到微孔Vj(xj,yj)距离的倒数,与迭代次数k无关,即

(5)
式(3)中:α为信息素影响因子,反映信息素浓度对于路径选择概率的影响程度;β为距离影响因子,反映微孔间距离对于路径选择概率的影响程度。
最终,取k代路径方案中的最优方案,即最短路径及对应的微孔检测顺序作为算法结果。
2.3算法改进研究
传统蚁群算法有其独特的优势,可利用逐代进化的方法不断逼近最优解,但也有一定的局限性。首先,为追求较高精度,往往需要设置较大的人工蚂蚁个数和迭代次数,这无疑增大了计算机的运算负担,消耗了大量的运算时间;其次,由于蚁群算法信息素采用正反馈方式不断更新,结果易陷入局部最优。针对这2个缺陷,本文研究所采用的算法在传统蚁群算法中作了如下改进。
2.3.1信息素浓度表初始化
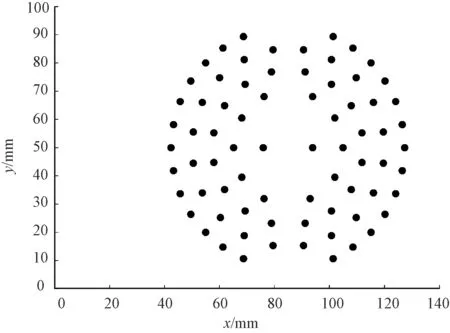
传统蚁群算法的初始信息素浓度矩阵中各元素相等,这会导致算法在初始迭代中缺乏目的性,使得收敛速度慢,效率低,故采用最近邻法对蚁群算法初始信息素浓度表的取值进行设置,由此提高算法效率。最近邻法是指从原点出发的微孔路径规划中,选择满足后一微孔是未检孔中距前一孔最近微孔的路径,例如对于图3所示随机微孔分布形式(横、纵坐标分别表示各微孔相对于电动机运动起点的x方向与y方向距离),图4示出其对应的最近邻路径。

图3 随机微孔分布Fig.3 Random micropore distribution
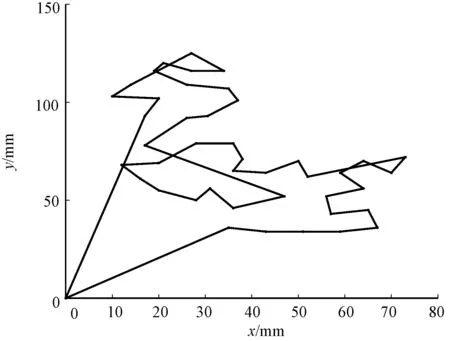
图4 最近邻路径及微孔遍历顺序Fig.4 Nearest neighbor method and traversal order
最近邻算法具有计算便捷但只能求得唯一次优解的特点,其本身作为一种路径规划算法是相对简单的,但非常实用,其结果常优于绝大多数可行解。将其结果作为蚁群算法初始全局最优路径,并相应调整初始信息素浓度,将使蚁群算法在前期若干代路径规划中的路径优化程度得到提升,从而在不增加迭代次数和人工蚂蚁个数的情况下提高算法效率。
同时,虽然可利用设置距离影响因子β与信息素影响因子α的比值调整微孔间距离对于路径点选择概率的影响程度,但若β与α比值较大,会导致在迭代过程的后期路径规划仍受微孔间距离的较大影响,无法发挥蚁群算法的优势;若β与α比值较小,在迭代初期又易导致路径选择的盲目性,使算法收敛速度过低。引入最近邻算法得到的结果作为蚁群算法初始信息素浓度设置的依据,不仅将使迭代初期的路径选择更具有目的性,也能避免迭代后期微孔间距离对路径选择概率的过大影响,同时也可分担信息素影响因子α和距离影响因子β的调节作用,从而为这2个参数的设置提供便利。
2.3.2算法结果的进一步优化
由于蚁群算法易陷入局部最优的缺点,有时得到的结果仍有一定的改进空间,故采用去尖端法对蚁群算法的结果进一步优化,其原理如图5所示。

图5 去尖端法原理Fig.5 Principle of path peaks removal method
设蚁群算法求得的最优遍历路径为O,P1,…,Pi-1,Pi,Pi+1,…,Pj-1,Pj,Pj+1,O,包含连线段Pi-1Pi,PiPi+1,PjPj+1。从图5中可看到,微孔Pi处的检测路径呈现“向内尖端”,可进一步优化。
如果满足:
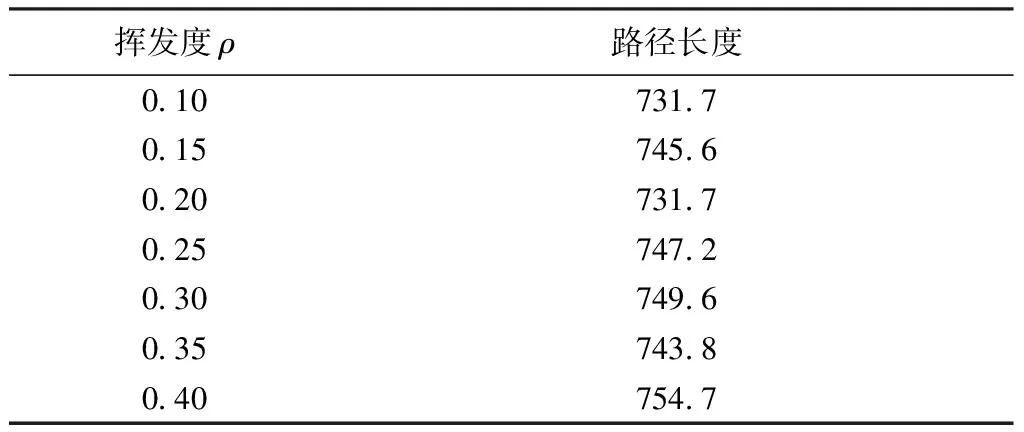
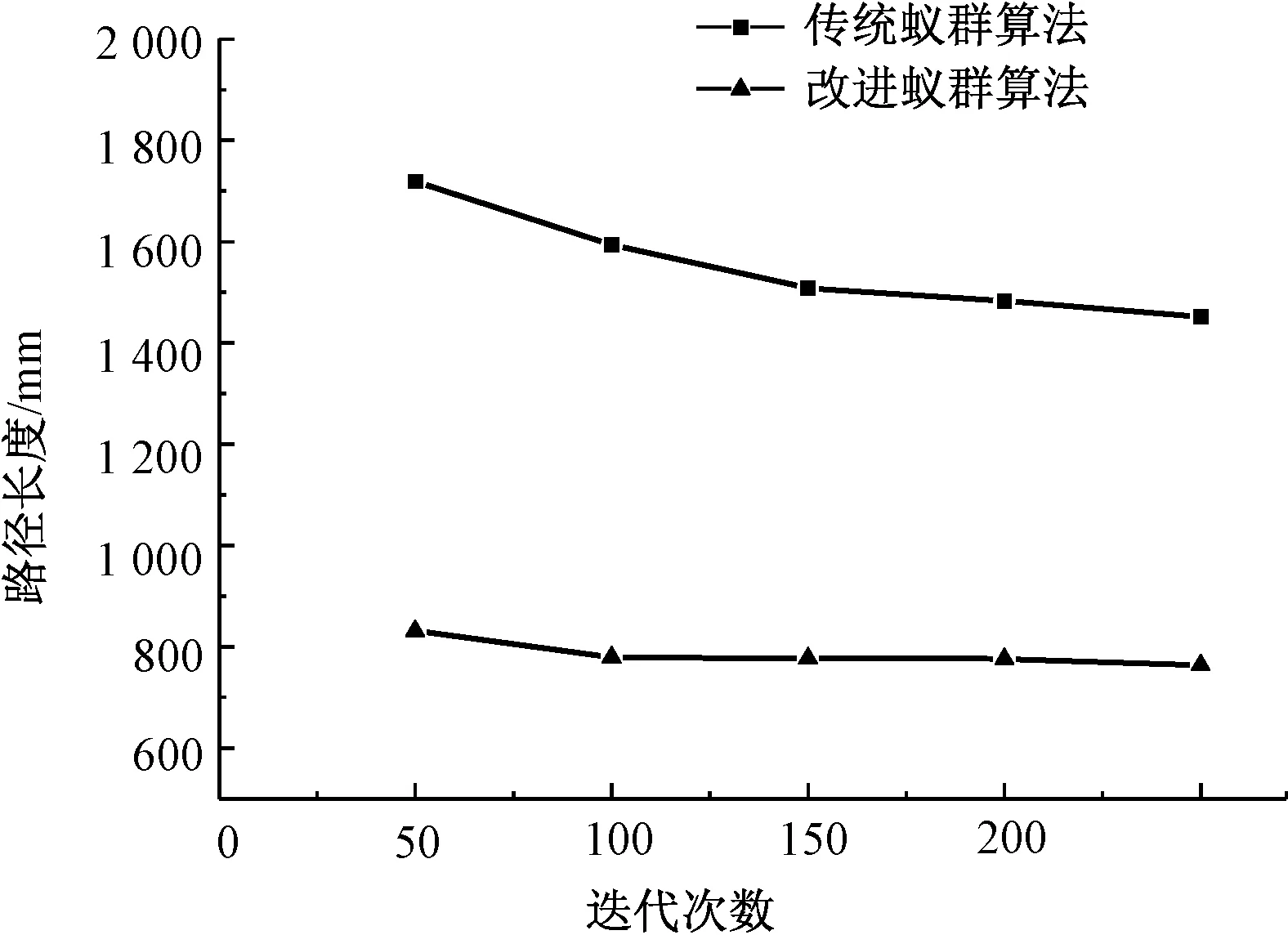
dPi-1,Pi+1+dPj,Pi+dPi,Pj+1 (6) 式中d为式(1)定义的微孔间距离,则去除原检测路径中的连线段Pi-1Pi、PiPi+1、PjPj+1,并替换为连线段Pi-1Pi+1、PjPi、PiPj+1。对整条路径上所有满足式(6)中对于Pi要求的点均做类似处理,从而实现总检测路径长度的降低。 2.4算法流程 本文研究设计的算法流程如图6所示。 图6 算法流程Fig.6 Algorithm flow 主要包括3部分:采用最近邻法求初始可行检测路径并初始化信息素浓度表;主体优化算法(蚁群算法);利用去尖端法对结果进一步优化。 为验证改进蚁群算法的优化效果,利用MatLab编程实现该算法。图7示出典型的微孔同心分布喷丝板,其上共有 74 个微孔,喷丝板的一端为入料端,边缘直径为104 mm,孔径约 3 mm,另一端为出料端,边缘直径为94 mm,孔径约为 0.4 mm。图8示出对应的微孔分布图(以电动机运动起点为坐标原点,固定喷丝板后,微孔坐标如表2所示)。 图7 微孔同心分布喷丝板Fig.7 Concentric spinneret. (a) Feed surface; (b) Discharge surface 图8 微孔分布形式Fig.8 Distribution of micropores 挥发度ρ是蚁群算法中的关键参数。若挥发度ρ取值较大,虽能使算法收敛速度提高,但极易导致陷入局部最优;若取值较小,需牺牲一定的算法时间,但可有效降低算法过早陷入局部最优的风险。为避免算法过早陷入局部最优,将ρ的取值范围初步限定在0.1~0.4之间。进一步,在α=2,β=1,人工蚂蚁个数m=100,总迭代次数K=500的条件下,利用MatLab计算不同ρ值对应的路径长度,结果如表3所示。由表可知,在该参数条件下,ρ值取0.1与0.2时算法结果较优。同时,挥发度ρ取0.2时,算法具有更高的收敛速度,因此,选择0.2作为验证算法中挥发度ρ的取值。信息素影响因子α与距离影响因子β决定了微孔间距离对于路径点选择概率的影响程度。由2.3.1小节可知,最近邻法设置初始信息素浓度使结果对于它们的敏感程度大大降低,经测试后在验证算法中取α=2,β=1。 表2 微孔位置坐标Tab.2 Micropore coordinates mm 表3 不同ρ值对应的路径长度Tab.3 Route lengths under different ρ values mm 对图8所示的微孔分布形式分别采用常规的逐圈向内检测路径[13]、最近邻检测路径、传统蚁群算法检测路径 (ρ=0.2,α=2,β=1,人工蚂蚁个数m=200,迭代次数k=1 000) 以及改进蚁群算法规划检测路径 (ρ=0.2,α=2,β=1,人工蚂蚁个数m=200, 迭代次数k=1 000),由式(1)定义的距离分别计算总路径长度,并按电动机30 mm/s的平均移动速度计算平均检测时间。其中,由于传统蚁群算法和改进蚁群算法属于概率型算法,其结果具有不确定性,故分别运行10次取平均结果和最优结果。同时,为切合实际检测需求,检测路径由原点出发并最终返回原点。图9分别示出逐圈向内、最近邻、传统蚁群算法、改进蚁群算法所对应的检测路径方案(横、纵坐标分别表示各微孔相对于电动机运动起点的x方向与y方向距离)。 图9 不同检测路径Fig.9 Different inspection routes. (a) Lap by lap inspection route; (b) Nearest neighbor inspection path; (c) Unimproved ant colony algorithm inspection route; (d) Improved ant colony algorithm inspection route 运算结果如表4所示。由表可知,所提出的基于改进蚁群算法的同心圆微孔分布喷丝板检测路径优化方案相比于传统方法在算法结果上有着较大的改进效果。算法平均结果相比于逐圈向内和最近邻路径方案,路径长度缩短约18%,在相同的算法参数和迭代次数下提出的改进蚁群算法,相比于传统蚁群算法在结果上得到了很大的优化。 表4 各检测路径方案结果Tab.4 Results of different route planning method 注:设v电动机=30 mm/s。 为进一步比较改进算法与传统蚁群算法对于喷丝板微孔检测路径方案规划问题的收敛性能,分别改变传统蚁群算法及改进蚁群算法的迭代次数,所得结果如图10所示。由图可知,改进蚁群算法不仅在结果上显著优于传统蚁群算法,且在收敛速度方面也有较大优势。 图10 算法性能比较Fig.10 Performance comparison of improved and unimproved ant colony algorithms 针对提高微孔同心分布喷丝板的检测效率问题,提出了一种基于改进蚁群算法的微孔检测路径规划方法。研究结果表明:1)最近邻法设定初始信息素浓度表可显著提高蚁群算法的收敛速度;2)路径尖端去除处理可进一步优化蚁群算法计算结果,缩短路径长度;3)改进的蚁群算法对于典型的微孔同心分布喷丝板检测路径规划是有效的,所得路径相比传统逐圈向内检测路径在长度上可缩短约18%。 FZXB [1] 谭志银. 非织造熔纺喷丝板自动化检测与加工技术的研究[D]. 上海: 东华大学, 2009: 1-3. TAN Zhiyin. Research on automated technologies inspecting and machining spinneret for melt-spun nonwoven[D]. Shanghai: Donghua University, 2009: 1-3. [2] SUN Lijun. Genetic algorithm for TSP problem[C]// Proceedings of 2015 International Industrial Informatics and Computer Engineering Conference. Xi′an: International Informazation and Engineering Associations, 2015. [3] GAO Ye, XUE Rui. An improved simulated annealing and genetic algorithm for TSP[C]// Proceedings of 2013 5th IEEE International Conference on Broadband Network & Multimedia Technology. Guilin:IEEI Beijing Section, 2013. [4] 邓义成, 任声策, 殷旅江. 基于改进果蝇算法的旅行商问题[J]. 兰州理工大学学报, 2016, 42(4): 109-114. DENG Yicheng, REN Shengce, YIN Lüjiang. Improved fruit fly optimization algorithm-based traveling salesman problem[J]. Journal of Lanzhou University of Technology, 2016, 42(4): 109-114. [5] DORIGO Marco, STUTZLE Thomas. Ant Colony Optimization[M]. Cambridge: MIT Press, 2004. [6] SUN Fanrong, HAN Songchen, QIAN Ge. Departure trajectory design based on pareto ant colony algorithm[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2016, 33(4): 451-460. [7] WANG Yanxia, QIAN Longjun, GUO Zhi, et al. Weapon target assignment problem satisfying expected damage probabilities based on ant colony algorithm[J]. Journal of Systems Engineering and Electronic, 2008, 19(5): 939-944. [8] ZHOU Binghai, YU Jiadi. Buffer allocation method of serial production lines based on improved ant colony optimization algorithm[J]. High Technology Letters, 2016, 22(21): 113-119. [9] SONG Jinjuan, BAI Yanping. An improved ant colony algorithm and its application in optimal routing problem[J]. Journal of Measurement Science and Instrumentation, 2013, 4(1): 23-29. [10] GAN Rongwei, GUO Qingshun, CHANG Huiyou, et al. Improved ant colony optimization algorithm for the traveling salesman problem[J]. Journal of Systems Engineering and Electronics, 2010, 21(2): 329-333. [11] YANG Jinhui, SHI Xiaohu, MAURIZIO Marchese, et al. An ant colony optimization for generalized TSP problem[J]. Progress in Natural Science, 2008(18): 1417-1422. [12] 吴华锋, 陈信强, 毛奇凰, 等. 基于自然选择策略的蚁群算法求解TSP问题[J]. 通信学报, 2013, 34(4): 165-170. WU Huafeng, CHEN Xinqiang, MAO Qihuang, et al.Improved ant colony algorithm based on natural selection strategy for solving TSP problem[J]. Journal on Communications, 2013, 34(4): 165-170. [13] 冯培, 刘家强, 裘大洪,等. 基于机器视觉系统对喷丝头微孔的自动检测[J]. 合成纤维工业, 2012, 35(1): 64. FENG Pei, LIU Jiaqiang, QIU Dahong, et al. Automatic detection of spinneret microhole by machine vision system[J]. China Synthetic Fiber Industry, 2012, 35(1): 64. Routeplanningforconcentricspinneretinspectionbasedonimprovedantcolonyalgorithm GUO Junxia, TAO Jianfeng, LIU Chengliang (SchoolofMechanicalEngineering,ShanghaiJiaoTongUniversity,Shanghai200240,China) In order to improve the inspection efficiency of concentric-distribution spinneret, an inspection route planning method based on improved ant colony algorithm was proposed. In order to overcome the shortcomings of conventional algorithm including low convergence speed and sinking into local optimum, this method redefined the distance between micropores to meet the characteristic of typical spinneret inspectors, set up the initial pheromone concentration table by the nearest neighbor method to obtain better results with other parameters unchanged, and further optimized the results by path peaks removal process. To verify the effectiveness of the proposed algorithm, calculation of the route planning for a typical concentric-distribution spinneret was carried out. The results show that the proposed algorithm has higher convergence speed, and it can shorten the route length by about 18% compared with the conventional inspection route and improve the inspection efficiency of matching spinneret. spinneret inspection; ant colony algorithm; pheromone concentration; nearest neighbor; optimization 10.13475/j.fzxb.20170201208 TS 173.8;TP 391 A 2017-02-10 2017-05-30 郭隽侠(1993—),男,硕士生。主要研究方向为机器人轨迹规划与机器视觉。陶建峰,通信作者,E-mail:jftao@sjtu.edu.cn。
3 算法验证




4 结 语

