过饱和状态下城市路网控制子区动态划分方法
,
(浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
过饱和状态下城市路网控制子区动态划分方法
沈国江,吴佳浩
(浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
过饱和状态下城市路网的控制子区划分是实施高效信号控制的必要基础.根据城市路网过饱和状态下交通流的特点,结合路口饱和度和车辆排队情况,提出了一种路口过饱和状态识别方法,并进一步将过饱和路口划分为三个不同的拥堵等级.在引入路段车辆容量比和路段交通需求影响度的基础上,采用模糊控制算法对相邻路口关联度大小进行计算.基于路口拥堵等级划分与相邻路口关联度提出一种子区分级动态划分策略,并给出一个完整的动态子区划分流程,最后通过算例说明了该控制子区划分方法的可行性.
过饱和;拥堵等级;关联度;模糊控制;动态划分
经济的快速发展和人民生活水平的不断提高带来了机动车保有量的高速增长,城市交通网络已经成为人们关注和研究的热点[1].过饱和交通流导致的车辆拥堵在大城市路网已成为常态.处于过饱和交通状态下的城市路网,其内部各区域有着不同交通特性(包括交通方式构成、交通量和流向等).为了取得更好的控制效果,需要将城市大规模路网划分为多个小范围的控制子区域[2].对此,国内外相关研究人员做出了许多研究:美国学者Walinchus[3]在1971年最先提出交通控制子区的概念,此后Yagoda[4]在子区划分指标问题上引入了“耦合度”的概念来判断两个路口是否需要进行协调,Chang[5]认为上游路口所采用的控制策略对下游相邻路口的关联度影响较大,并据此建立了关联度模型.随着控制要求的提高,研究内容从静态子区划分逐步转向对动态子区划分,王学堂[6]将整个区域复杂系统分解为若干个简单系统,再对各个子系统进行研究.尚德申等[7]以静态分区为出发点,实现了动态分区的过程.段后利等[8]提出了可协调度的概念并引进超图理论将其用于子区划分算法中.卢凯等[9]采用子区划分模型进行子区划分,并以遗传算法为基础,采用降维方法对划分方案的解进行快速寻优.以上研究主要针对非过饱和交通状态,随着交通堵塞现象变得越来越频繁,主要体现在城市出行高峰时主干道的车辆拥堵等.杨晓光等[10]对路网设定了消散、过渡、阻塞和常态四个控制区域,进而提出过饱和状态下交通控制小区的动态划分方法.李轶舜等[11]提出了以交通需求超过通行能力的关键路口为中心的多层边界控制策略,动态确定控制边界.
笔者主要依据路口饱和度和路段进口道车辆排队情况,提出了一种对路口过饱和状态的识别方法,并进一步给出了一种过饱和路口按拥堵等级分类的方法.在计算相邻路口关联度的过程中,提出路段交通需求影响度的概念,并结合路段车辆容量比,采用模糊控制算法完成对相邻路口关联度大小的计算.提出一种子区分级动态划分策略,并给出一个完整的动态子区划分流程,最后进行算例分析.
1 研究思路
路网中的区域拥堵一般是从单个路口的交通拥堵开始,路口长时间处于过饱和状态引起车辆排队长度不断增长,进而引起路段的阻塞,因此需要对路网中的路口进行过饱和状态识别,并且需要根据这种识别方法对路口拥堵等级进行分级.相邻路口关联度是定量描述相邻路口间交通流相关性的一个交通参数,反映了不同信号控制方案及路段交通状态对相邻路口间关联程度的客观影响[12].结合实时路段车辆容量比与路段交通需求大小来分析相邻路口关联度的高低.城市路网处于过饱和状态时交通流特性较为复杂,需要将区域内所有路口作为一个整体进行协调[13-14],各区域的拥堵程度各不相同,为取得较好的控制效果,考虑根据划分起点路口的拥挤度将路网划分为不同拥堵等级的控制子区,以便于在实施信号控制时采取不同的控制策略.
过饱和控制子区划分总体流程如图1所示.

图1 过饱和控制子区划分总体流程Fig.1 Overall flow of subarea division under oversaturated condition
2 路口过饱和状态识别与分级
2.1 基本判别指标定义
以往的研究[10-11]主要将识别路段过饱和状态作为子区划分起始步骤,而对路段的饱和状态识别主要基于排队长度,笔者将以对路口过饱和状态的识别作为子区划分的切入点,并结合路口饱和度与车辆排队长度对路口过饱和状态进行识别.单路口结构与部分排队车辆如图2所示,并假设:同一个流向不会在一个周期中不同的两个相位中出现.
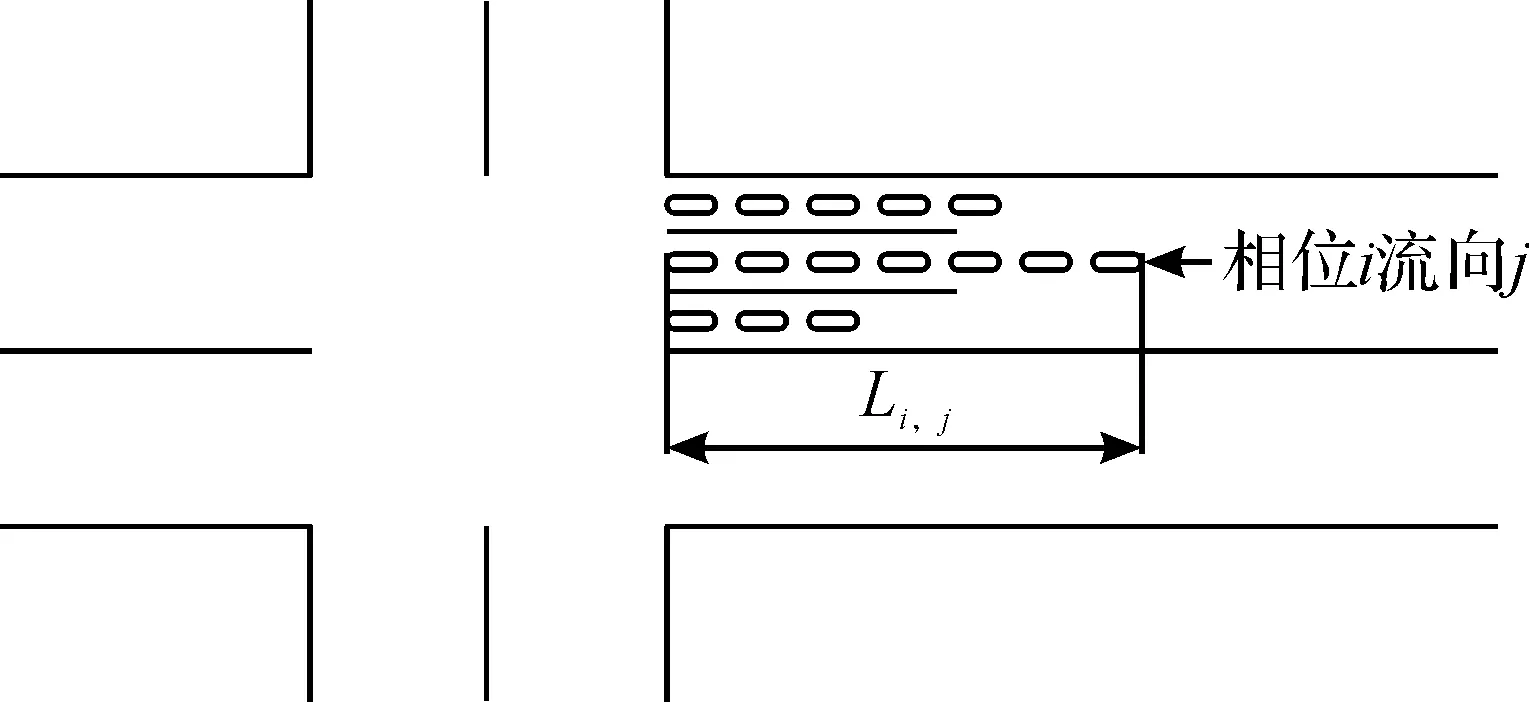
图2 路口饱和状态识别示意Fig.2 Recognition of intersection’s saturation
定义相位i流向j的饱和度为

(1)
式中:qi,j为相位i的流向j到达路口的交通流量,veh/h;Ci,j为相位i流向j的通行能力,veh/h;λi为相位i的绿信比;qs,i,j为相位i流向j的饱和流量,veh/h.
继而可以计算相位饱和度xi与路口饱和度x,即
(2)
(3)
式中:J为相位i的流向总数;I为路口信号方案的相位总数.
取绿灯结束时,相位i流向j对应进口道车辆排队比,即
(4)

2.2 路口过饱和状态识别方法与拥堵分级
对路网中所有路口进行过饱和状态识别,并进一步将路网中达到过饱和状态的路口按各自拥堵情况进行分类,主要将过饱和路口分为Ⅰ,Ⅱ,Ⅲ三个等级,拥堵级别依次降低,没有达到过饱和状态的路口不对其划分等级.

当路口饱和度x超过一定上限时,表明路口已经达到饱和状态.依据直接影响路口饱和度x的进口道车辆排队比的大小,将路口分为两个饱和程度不同的等级,假定:

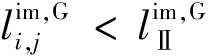
由此得判别路口等级大小的充分必要条件为




3 相邻路口关联度分析
路口关联度是子区进行扩散的重要指标,关联度计算直接影响子区划分效果,而路段中车流饱和程度反映了城市道路空间的使用情况,过饱和状态下路段中车流饱和程度较大,会造成较大范围的车辆延误[15].在此引入路段车辆容量比这个指标来衡量路段中车流的饱和程度,将其作为计算关联度的一个因子.此外,分析路口间关联度大小还需考虑短时内(1~2个周期)进入该路段的车辆数,在此引入路段交通需求影响度这个指标来衡量短时内即将进入路段的车辆数,并将其作为计算关联度的另一个因子.还应考虑路段过短或过长都对路口关联度有较大的影响.将路口间关联度记为D,路段车辆容量比记为C,路段交通需求影响度记为I.
3.1 关联度分析总体路线
首先判断路段长度LR是否小于一个路段长度极小值LR,min(通常为200 m),若小于则将关联度设为1;同时设定一个路段长度极大值LR,max(通常介于800~1 000 m之间),超过极大值则关联度设为零.当路段长度处于一般区间(LR,min,LR,max)之内,将路段车辆容量比C和交通需求影响度I作为输入,通过模糊算法得到输出值,作为路口关联度大小.总体路线如图3所示.

图3 关联度分析总体路线Fig.3 Overall path of correlation analysis
3.2 路段交通需求影响度计算
笔者将路段交通需求影响度I与其所有进口的排队车辆数与当前路段剩余容量相关联,如图4所示,路段交通需求影响度I分别定义为

(5)

(6)
I=maxI1→2,I2→1
(7)


图4 路段交通需求影响度分析Fig.4 Influence degree of traffic demand analysis
3.3 路段车辆容量比计算
路段车辆容量比反应了当前路段车流所达到的饱和程度,主要与路段当前车辆数以及路段车辆容量有关.
路段车辆容量比C定义为

(8)
式中:x,y为两个相邻路口的各自编号;Nx→y为路口x到路口y方向路段容量;Nx→y,V为路口x到路口y方向路段上已存在车辆总数.
为了凸显路段交通需求的重要性,计算路段车辆容量比之前需要参照上行和下行路段各自的交通需求影响度,若该路段I=I1→2,则在计算时令x=1,y=2,否则取反.
3.4 路口间关联度模糊算法
将3.2与3.3中得到的路段车辆容量比以及路段交通需求影响度作为模糊控制器的2个输入参数,其各自模糊分割如图5(a,b)所示.图5(a)中将路段车辆容量比分割为{很小,小,较小,中等,较大,大,很大}7个模糊语言,图5(b)将路段交通需求影响度分割为{很低,低,中等,较高,高,很高}6个模糊语言.将路口关联度作为模糊控制器的输出,分割为5个模糊语言:{低,较低,中等,较高,高},如图5(c)中所示.模糊规则如表1所示,C,I分别为路段车辆容量比和路段交通需求影响度.
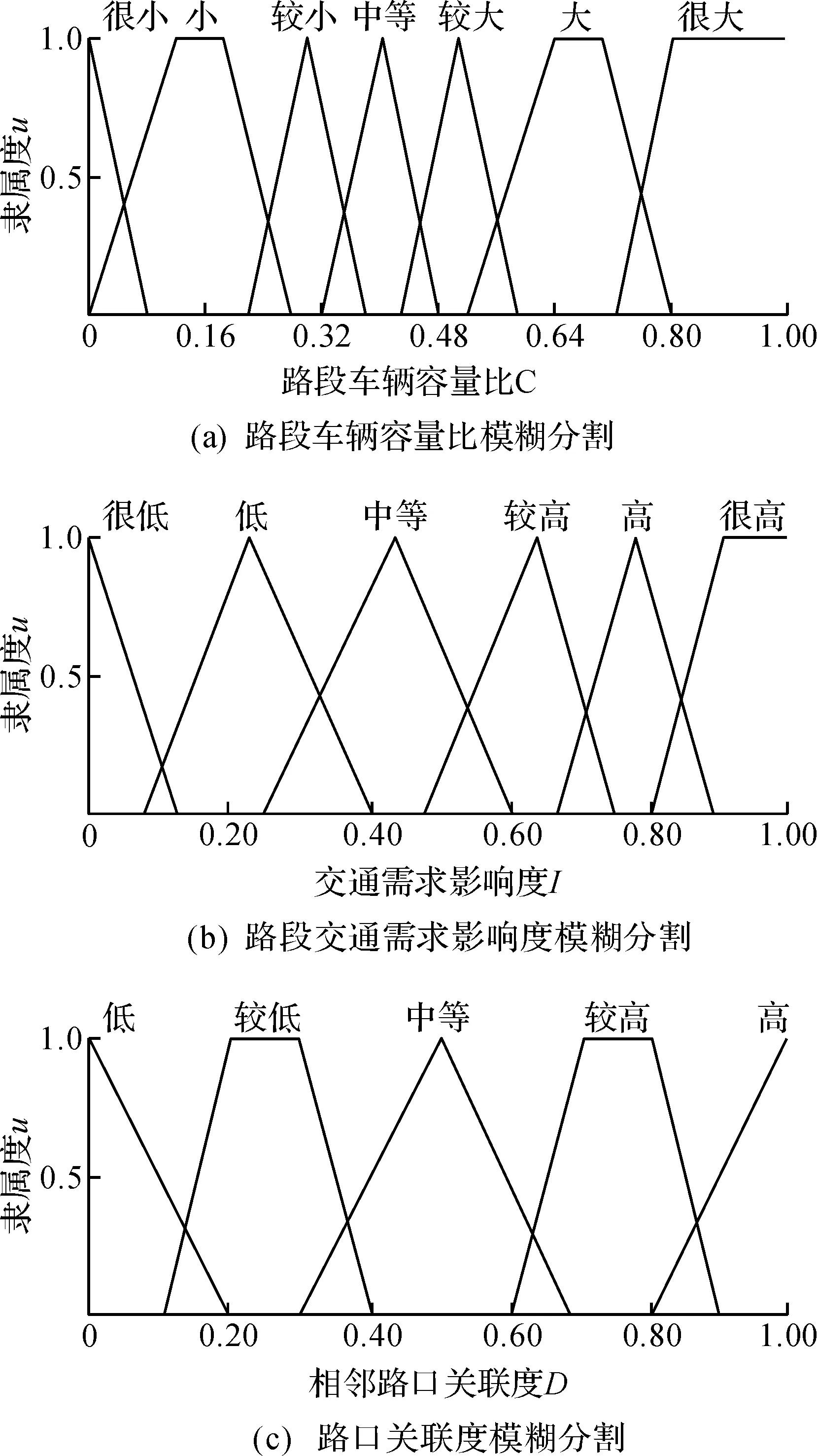
图5 模糊变量分割图Fig.5 Fuzzy variable segmentation

IC很大大较大中等较小小很小很高很高很高很高高较高中等中等高很高很高高较高中等中等中等较高很高高较高较高中等中等较低中等很高高较高中等中等较低低低高较高中等中等较低低低很低中等中等中等较低低低低
设定Dmax为路口关联度的一个临界值,一般取值为0.65.当D≥Dmax时,则认为对应两个相邻路口呈关联状态,继而在划分子区过程中将被无条件划分到同一个过饱和子区中.若D 4.1 过饱和控制子区划分基本原则 上述将过饱和路网中的过饱和路口划分为三个拥堵等级,拥堵等级由大到小为Ⅰ级,Ⅱ级,Ⅲ级.将这三个拥堵等级的路口作为子区划分的起点,划分的优先权大小与其拥堵等级成正比,即先以路网中的Ⅰ级路口为划分起点进行子区划分,且一个路口只能被进行一次划分,不可重复;当所有Ⅰ级路口都划入子区后,再以剩下的Ⅱ级路口为起点开始进行划分,最后以Ⅲ级路口作为起点进行划分.与以往过饱和子区划分不同的是:由于要以输出不同拥堵等级的子区为最终目标,笔者根据子区划分起点路口拥堵等级大小而采用适合自身的子区扩散阈值,即以Ⅰ级路口,Ⅱ级路口分别作为划分起点划分时,Dmax的取值可能各不相同,选用各自的路口关联度阈值作为子区扩散条件. 4.2 过饱和控制子区划分算法具体流程 具体流程如下: Step1获取路网实时数据,采用上述单路口过饱和状态识别方法分别识别路网中的Ⅰ,Ⅱ,Ⅲ级路口,放入到一个集合Mk中.对所有路段进行关联度分析,计算关联度值.令j=k=0. Step2令s=i=0. Step3取Mk中任意一个等级最高的路口mk作为划分起点,将mk放入集合Ai. Step4取Ai中任意路口ai,s的相连路口关联度的值. Step5将关联度超过阈值的路段的相连路口放入集合B. Step6判断Ai是否完成全部遍历,若没有,则s=s+1并回到Step 4,若已经遍历完毕,则进入Step 5. Step7令集合C=B-Ai∪Ai-1∪…∪A0,判断集合C是否不为空,若为空则进入Step 6,否则进入Step 7. Step8令i=i+1,将集合C中路口放入集合Ai,清空集合B,C,令s=0,回到Step 4. Step9令Tj=A0∪A1∪…∪Ai,再将A0,A1,…,Ai都置为空. Step10依据划分起点的拥堵等级判断Tj的等级. Step11k++,j++,令Mk=Mk-1-Mk-1∩Tj-1,判断Mk是否为空,如果不为空,则回到Step 2,如果为空,则子区划分结束,得到的子区分别为T1,T2,…,Tj-1. 基于过饱和子区划分基本原则,得出具体过饱和子区划分流程如图6所示,识别子区Tj等级的具体步骤:查找中拥挤度等级最高的路口,若最高属于Ⅰ级路口,则对应为高过饱和控制子区,若Ⅱ级路口则对应为中过饱和子区,若Ⅲ级路口则对应为低过饱和子区. 图6 过饱和控制子区具体划分流程Fig.6 Process of oversaturated control subarea division 5.1 算例描述 本算例采用VISSIM 4.3交通仿真软件,基于某市的部分路网及检测到的流量数据,路网内主要路段长度位于210~540 m之间,该路网结构如图7所示,划分子区前的信号方案为实际路网实时所用方案,所取用的是早高峰内30 min的流量数据.13个流量输入,q按下标1~13分别为1 101,804,1 249,783,1 588,847,1 500,1 139,1 454,1 607,1 433,1 128,1 440 veh/h,各个路口的车流转向比基本采用实际检测数据.此外用Matlab软件对子区划分算法进行编程实现. 图7 路网结构及流量输入Fig.7 Road network and the flow input 5.2 算例划分算法分析 在仿真过程中,从路口r6发生溢出状态时进行子区划分算法的分析,取出各路段在该时刻的道路容量比及交通需求影响度进行计算,分析所得各路段关联度如图8所示. 图8 路网关联度计算结果Fig.8 Result of the correlation analysis 图9 子区划分结果Fig.9 Result of the subarea division 记r1与r5之间的横向路段为D1,记r6与r9之间的横向路段为D2,实际情况中D1,D2都是所在区域的主干道,不同的是前者的道路较宽,在流量相差不多的情况下其整体的饱和度没有后者高,且路段D2的高饱和集中表现在流向q12所在流向,因此有必要将其整条路段划分在同一个子区内,而又因为高峰期期间,r1至r6与r2至r7之间的车流较多,实际上有必要将r1与r2划分为同一子区.综上,实际情况与研究所得划分结果一致,算法经仿真分析较为可靠. 提出的过饱和状态下交通控制子区划分方法主要考虑了过饱和路网各局部饱和程度的差异性,实现了过饱和状态下控制子区动态分级划分方法的量化与系统化.在设计路口过饱和状态识别策略以及对相邻路口间关联度的分析计算上有所创新,所用 算法简洁高效,能满足较高的实时性要求.但是若要在实际运用中更加高效合理,还需对子区划分阈值的选取进行更多理论与实践研究. [1] 杨旭华,李传告,陈光.基于K-最短路径的交通网络传输性能分析[J].浙江工业大学学报,2014,43(3):249-252. [2] SHU Lin,BART D S,YU G X,et al.Efficient network-wide model-based predictive control for urban traffic networks[J].Transportation research part C,2012(1):122-140. [3] WALINCHUS R J.Real-time network decomposition and subnetwork interfacing[M].Washington D C:Transportation Research Board,1971:20-28. [4] YAGODA H N, PRINCIPE E H, VICK C E, et al.Subdivision of signal systems into control areas[J].Traffic engineering,1973,43(12):42. [5] CHANG E C P.How to decide the interconnection of isolated traffic signals[C]//Proceedings of the 17th conference on winter simulation.New York:ACM,1985,445-453. [6] 王学堂.城市交通信号整体优化理论的概念与方法[J].长安大学学报(自然科学版),2002,22(5):92-94. [7] 尚德申,石建军.交通控制区域动态划分研究[J].道路交通与安全,2007(1):27-29. [8] 段后利,李志恒,张毅,等.交通控制子区动态划分模型[J].吉林大学学报(工学版),2009,39(S2):13-18. [9] 卢凯,徐建闽,郑淑鉴,等.协调控制子区快速动态划分方法研究[J].自动化学报,2012,38(2):279-287. [10] 杨晓光,黄玮,马万经.过饱和状态下交通控制小区动态划分方法[J].同济大学学报(自然科学版),2010,38(10):1450-1457. [11] 李轶舜,徐建闽,王琳虹.过饱和交通网络的多层边界主动控制方法[J].华南理工大学学报(自然科学版),2012,40(7):27-32. [12] 沈国江,钱晓杰.主干道动态协调控制技术[J].控制与决策,2013,28(12):1908-1911. [13] 沈国江,陈文峰.方案选择式区域协调控制方法及应用[J].浙江工业大学学报,2016,44(3):237-241. [14] 李澎林,张献力,李伟.基于双字Hash机制的交通信息分词算法研究[J].浙江工业大学学报,2014,42(6):596-600. [15] WANG Ping,JONES L S,YANG Qun,et al.Cell transmission model based traffic csignal timing in oversaturated conditions[J].Journal of central south university,2013,20(4):1129-1136. Dynamicdivisionmethodofurbantrafficnetworkcontrolsubareaunderoversaturatedstate SHEN Guojiang, WU Jiahao (College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China) The division of subarea is a vital base for implementing the control of traffic signal efficiently under oversaturated state. Based on the features of the oversaturated traffic flow, combining traffic saturation of intersection and the vehicle queue length, this paper proposed a method to recognize the oversaturated state of single intersection, and these oversaturated intersections are divided into three different congestion levels. By introducing the road traffic capacity and road traffic demand impact, the fuzzy control algorithm is used to, calculate the correlation of adjacent intersections. Based on three different congestion levels and the correlation of adjacent intersections, this paper proposed a dynamic division strategy and put out a complete dynamic subarea division process. Finally, the feasibility of the subarea division method is illustrated by an example. oversaturated state; congestion level; correlation; fuzzy control; dynamic division 2016-12-23 国家自然科学基金资助项目(61174174);浙江省科技厅公益技术研究工业项目(2015C31059);浙江省交通运输厅科研计划项目(2014T08) 沈国江(1975—),男,浙江绍兴人,教授,博士后,研究方向为城市道路交通建模、优化与控制技术等,E-mail:gjshen1975@zjut.edu.cn. TP273 A 1006-4303(2017)06-0591-06 (责任编辑:陈石平)4 过饱和控制子区划分方法
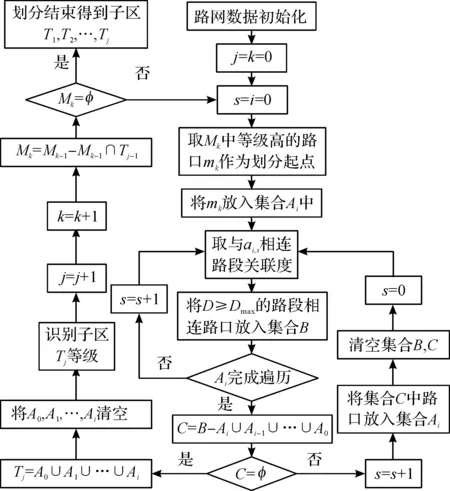
5 划分算法算例分析




6 结 论

