砾石土心墙堆石坝心墙孔隙水压力分析

倪 沙 沙， 迟 世 春

( 大连理工大学 建设工程学部 水利工程学院, 辽宁 大连 116024 )

砾石土心墙堆石坝心墙孔隙水压力分析

倪 沙 沙， 迟 世 春*

( 大连理工大学 建设工程学部 水利工程学院, 辽宁 大连 116024 )

土石坝的碾压施工会在大坝心墙中产生较高的超静孔隙水压力．对高土石坝，施工期心墙内产生的超静孔隙水压力难以有效消散，使得心墙内长期存在较高的孔隙水压力，导致其有效应力降低，影响心墙的工作性态和大坝稳定性．以某砾石土心墙监测资料为基础，分析了心墙填筑及水库蓄水对孔隙水压力及其变化的影响．提出了一种计算堆石坝心墙孔隙水压力消散的简化方法，即竖向受压而水平排水的一维固结方法．将其应用于心墙填筑完成后库水位保持不变时段的心墙孔隙水压力消散计算，通过计算值与实测值的比较，验证了心墙孔隙水压力简化计算方法的合理性；并进一步计算了心墙测点的固结过程，发现其固结度达到95%所需的时间长达10～30 a，其中前10 a各测点的固结度均已达到了70%．

砾石土心墙；孔隙水压力；监测；一维固结；固结度

0 引 言

压实后的砾石土防渗体强度高、压缩性低，可有效降低坝壳料对心墙的拱效应及水力劈裂的发生；可限制裂缝开展；对含水量不敏感，便于重型施工机械的运输和碾压．因此，国内外已建和在建的高土石坝越来越普遍采用砾石土作为防渗料．国外如苏联高300 m的努列克坝、印度高260 m的特里坝、美国高230 m的澳洛维坝等，国内如已建的高103 m的鲁布革堆石坝、高186 m瀑布沟堆石坝、高261.5 m糯扎渡堆石坝和在建的高314 m双江口堆石坝等[1-3]．

土石坝防渗料在上坝碾压时其饱和度通常达到90%以上，因此，在施工期心墙内容易产生较高的孔隙水压力，这会导致心墙中有效应力降低，进而影响坝体的稳定和强度．如挪威的海蒂朱维特坝，在施工过程中心墙内就产生了较高的孔隙水压力，而后虽变更设计将心墙宽度变小，仍在竣工1 a后因发生水力劈裂而出现了心墙破坏的事故[4]．因此，对高堆石坝施工期孔隙水压力的研究一直备受关注．陈立宏等[5]利用有限元固结程序计算并分析小浪底大坝心墙中的孔隙水压力，结果表明，大坝心墙在施工期内出现了较高的孔隙水压力，且实测超静孔隙水压力的消散比有限元计算预测的要缓慢．陈继平等[4]以瀑布沟堆石坝施工期的监测资料为基础，分析了上坝土料的含水量和施工进度对堆石坝心墙孔隙水压力的影响，并认为与施工速率相比，含水量是影响孔压的主要因素．郑俊等[6]分析了瀑布沟堆石坝心墙施工期孔隙水压力的特征与形成机制，认为对黏土心墙坝的认识和研究方法未必适用于砾石土心墙坝．

本文以某砾质心墙监测资料为基础，分析心墙填筑及水库蓄水对孔隙水压力及其变化产生的影响，提出一种计算堆石坝心墙孔隙水压力消散的简化方法，即竖向受压而水平排水的一维固结方法，应用于心墙填筑完成后库水位保持不变时段的心墙孔隙水压力消散的计算，并通过计算值与实测值的比较验证简化计算方法的合理性．

1 工程概况与监测布置

1.1 工程概况

某砾石土心墙堆石坝，心墙顶高程820.5 m，顶宽10 m，心墙基础最低建基面高程560.0 m，上下游坡度均为1∶0.2．为保护心墙土料，根据反滤设计原则，在心墙区上下游两侧均设置了Ⅰ、Ⅱ两层反滤料，在上下游反滤层Ⅱ与坝壳粗堆石料间设置了细堆石过渡料，以便保护Ⅱ层反滤料，同时可协调心墙与坝壳粗堆石体间的变形．根据粗堆石料分区优化的设计原则，将强度高、透水性好的优质堆石料布置在坝顶、坝壳外部及下游坝壳底部等对坝坡稳定及坝体抗震有重要影响的关键部位，而在坝壳内部采用强度指标稍低的次堆石料．心墙、反滤料Ⅰ、反滤料Ⅱ与基岩接触范围设置钢筋混凝土垫层，并在心墙下设置1～2排帷幕灌浆[7]．

大坝心墙自2009年开始填筑，经历3次雨季并在雨季暂停施工，2012年底填筑完成．大坝于2011年11月开始下闸蓄水，8个月后蓄水至死水位765 m附近并保持水位基本不变，2013年第二次蓄水．

1.2 心墙砾石土性状简介

心墙防渗土料为黏土质砂和含砂低液限黏土．天然土料颗粒级配细，黏粒含量偏高，防渗性较好，但力学性能特别是压缩性能难以满足高坝的筑坝要求，最终确定掺砾35%(质量比)．心墙掺砾料的设计指标为击实功2 690 kJ/m3，全料控制压实度不小于95%，含水率ω为(ωop-1%)～(ωop+3%)[8]．根据碾压试压，土料掺砾后碾压，掺砾土为天然含水，碾压后全料含水率ω为(ωop+2.7%)～(ωop+3.2%)，满足设计要求，无须调节土料天然含水率．根据心墙掺砾料的击实试验，在2 690 kJ/m3击实功下掺砾料最大干密度为2.01～2.15 g/cm3，平均为2.06 g/cm3，最优含水率为7.3%～9.6%，平均为8.8%．考虑到碾压后全料含水率大于最优含水率，则ρd<ρdmax，取干密度ρd=2.01 g/cm3．掺砾料的相对密度为2.68，可求得心墙压实后的孔隙比为0.33，饱和度为93.4%～97.5%．

由非饱和土力学知识可知，当土壤中的含水量很高时，土壤中的气相体积微小并被液体所包围，只能随液体一起流动，此时的土壤可视为一种挟气水的二相体系．该二相体系土壤气渗性极小，其有效应力表达式可视为与饱和土相同．通常认为饱和度高于95%的土可作饱和土处理．因此，该心墙料填筑后可近似看作处于饱和状态．

1.3 监测布置

心墙碾压填筑后近似饱和，而心墙填筑过程中由于其渗透系数很小，无法在短时间内将水挤出，从而在心墙内产生高孔隙水压力．为了监测心墙孔隙水压力变化情况，心墙填筑时在心墙3个断面内埋设了振弦式渗压计，如图1所示．

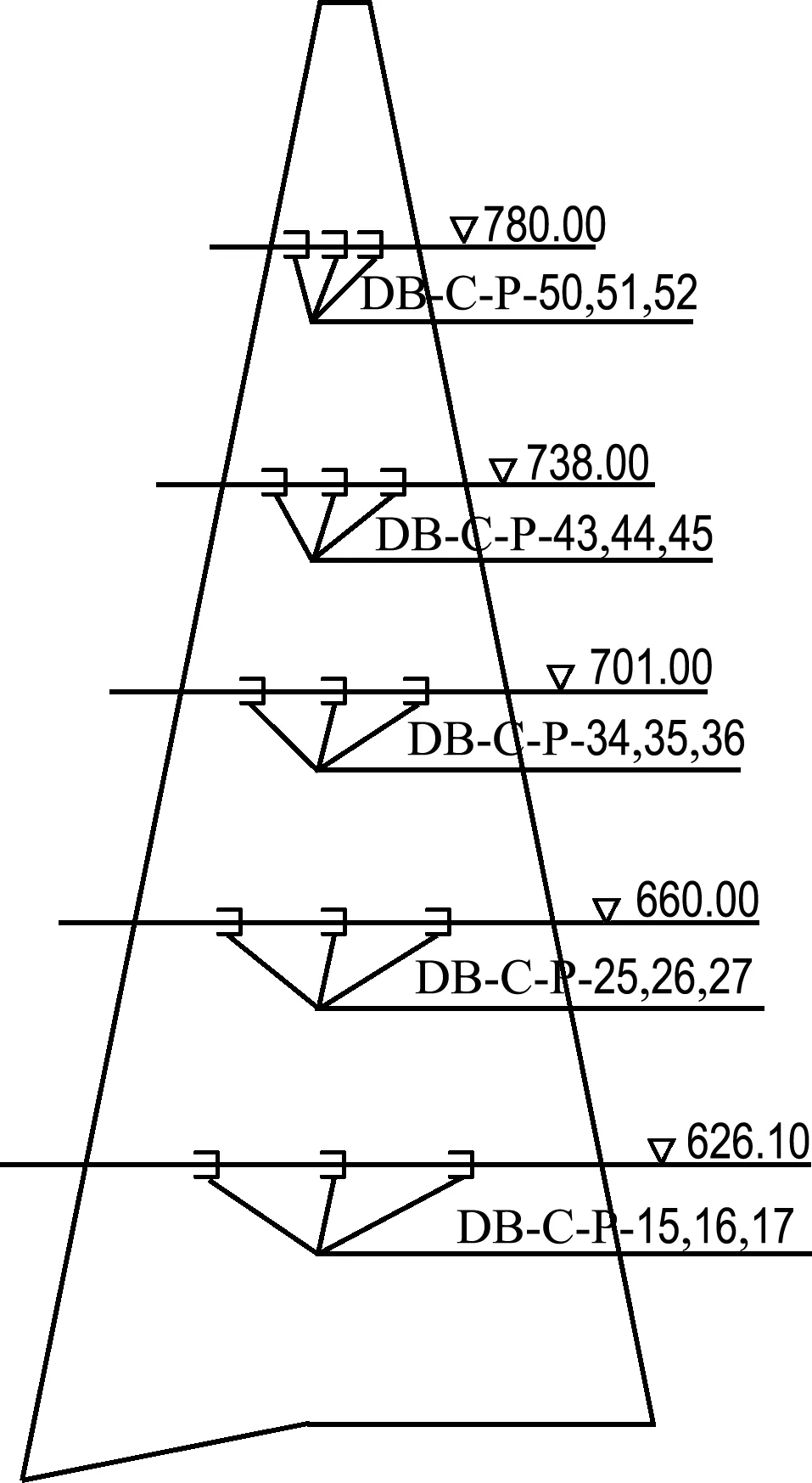
(a) C-C断面(0+309.60)

(b)A-A断面(0+169.36)

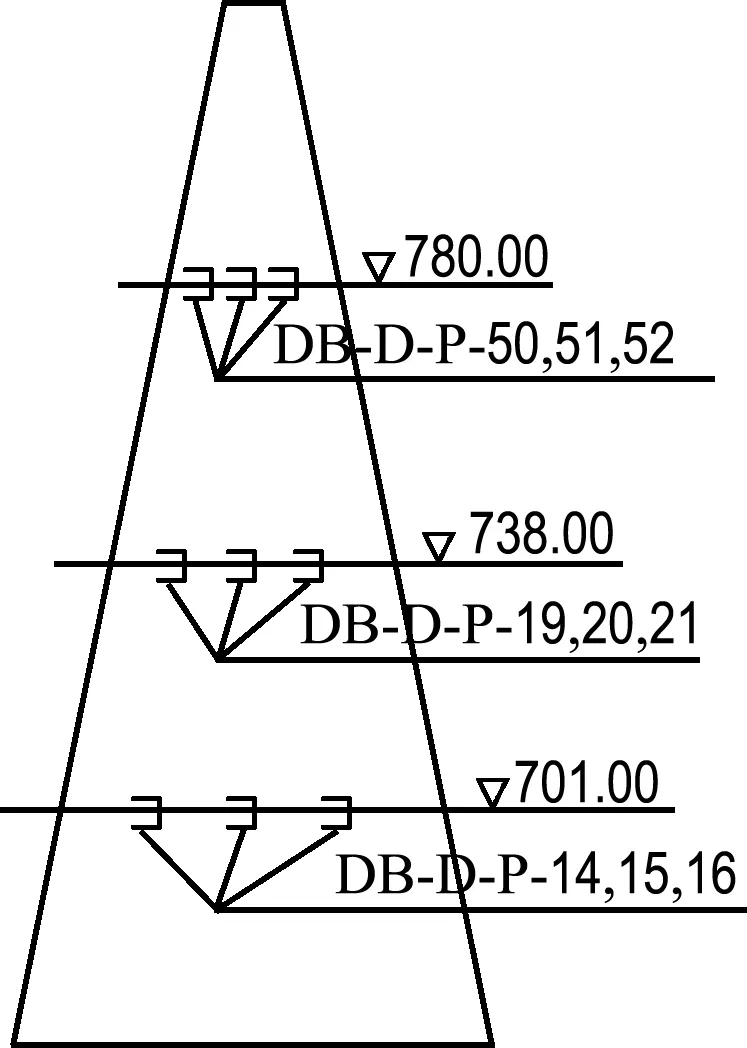
(c)D-D断面(0+482.30)

图1 心墙渗压计布置图

Fig.1 Layout of osmometers in core-wall

2 孔隙水压力变化与分析

3个断面内具有较完整观测数据的渗压计共计15个．为了分析心墙内孔隙水压力的变化规律，给出部分测点的渗压计实测水头-时间过程线，如图2、3所示．

由图2、3可以看出，渗压计埋设后孔隙水压力便开始增长，几乎没有滞后性，而后随心墙填筑及库水位变化而变化的规律相似．归纳如下：

图2 不同高程心墙内渗压计实测水头-时间过程线

Fig.2 Measured varying hydraulic head-time curves of osmometers at different heights in core-wall

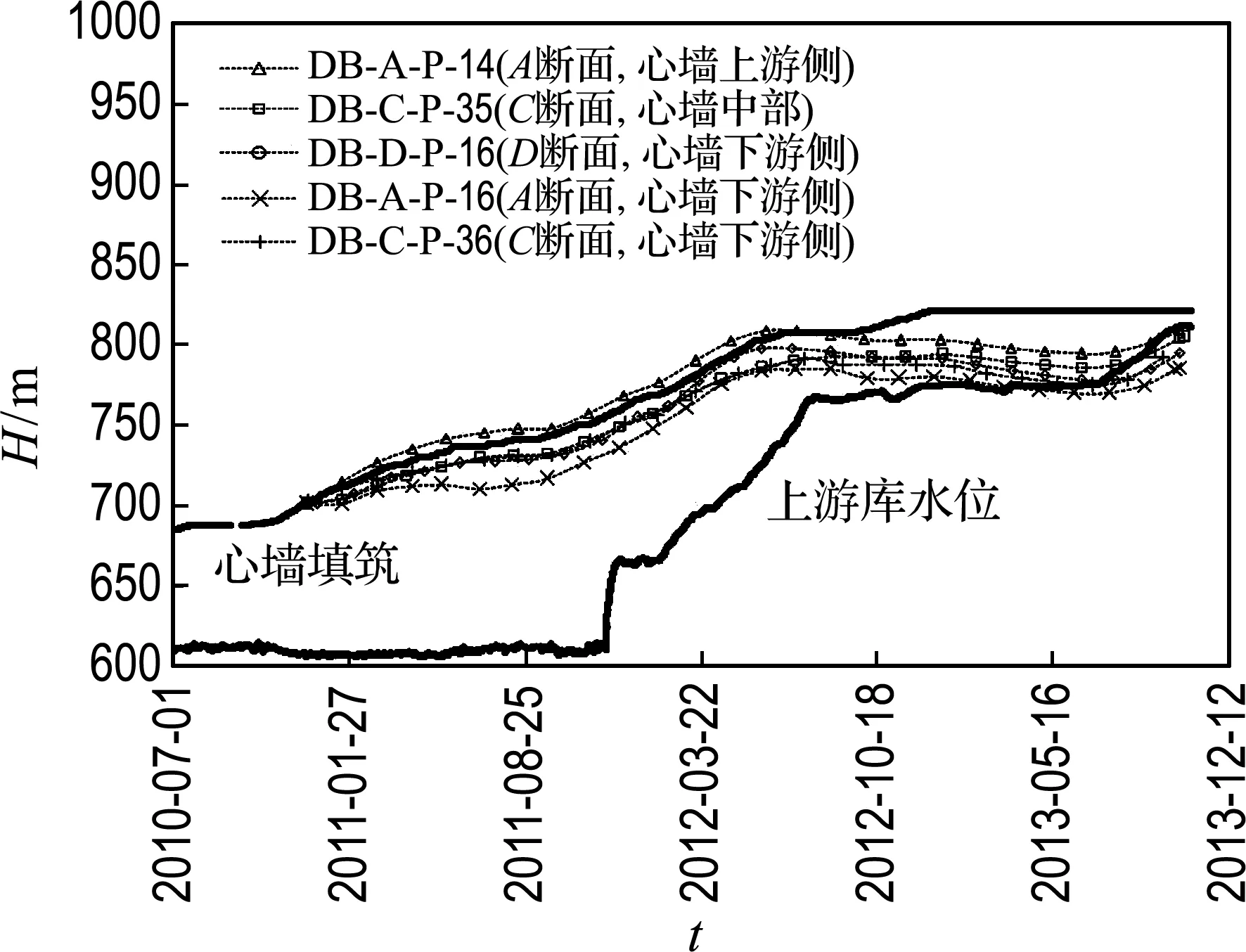
图3 701.00 m高程心墙内渗压计实测水头-时间过程线

Fig.3 Measured varying hydraulic head-time curves of osmometers at 701.00 m elevation in core-wall

(1)由图2不同高程心墙内部渗压计实测水头-时间过程线可以看出，测点高程越低，即上覆压力越大，心墙填筑完成时产生的孔隙水压力越高；由图2、3中同一高程心墙内部渗压计实测水头-时间过程线可以看出，相同高程不同位置测点的孔隙水压力，心墙上游侧>心墙中部>心墙下游侧．

(2)心墙填筑期，孔隙水压力随心墙填筑而增大，且增大速率与心墙的填筑速率有良好的相关性．当心墙填筑快时，孔隙水压力增长速率快；当心墙填筑慢或在雨季暂停填筑时，孔隙水压力保持不变或略有下降；在2012-07-01雨季来临大坝暂停施工(此时填筑高程约为807.68 m)时，孔隙水压力达到最大值．孔隙水压力随心墙填筑而增大的主要原因是在心墙填筑过程中，作用在土体上的总应力不断增大，使得土体骨架被压缩，土内孔隙体积减小，而孔隙内的水不能及时有效消散，导致原来由土体骨架承担的部分压力转由孔隙水承担．

(3)渗压计埋设后很快便能测得孔隙水压力，几乎没有滞后性，这主要是由于渗压计埋设时外面包裹一层渗透系数量级为10-4cm/s的细砂,其渗透系数远大于周围砾石土的渗透系数，使得细砂中的水可瞬间渗入渗压计内腔．

(4)大坝填筑完成后，心墙内孔隙水压力主要受上游库水位变化引起的作用在心墙上的荷载变化的影响，表现为上游库水位上升，作用在心墙上的荷载增大，心墙孔隙水压力的上升速度大于消散速度，从而使得心墙孔隙水压力上升．

3 竖向受压水平排水的一维固结微分方程

饱和土体的有效应力原理指出，由于水的压缩模量比土骨架高，当外载施加于土体后，土中水首先产生超静孔隙水压力，该超静孔隙水压力会使孔隙水沿着渗压梯度向低压区渗透，这就是超静孔隙水压力消散，同时作用于土骨架上的有效应力会增加以平衡外载．在孔隙水被挤出的同时，土体被不断压缩，直到超静孔隙水压力消散完毕，土体的压缩亦趋于稳定，这一过程称为固结．

固结过程中，孔隙水一定是沿着渗压梯度方向从孔压高处向低处渗透．具体到砾石土心墙，其填筑过程是竖向不断增加压力，竖向渗径也不断增长的过程．再加上当前的心墙施工碾压工艺使得心墙的竖向渗透系数比水平向小，一些坝水平渗透系数达到竖向的3～5倍．从心墙的剖面图(图1)可以看出，若考虑心墙外围的反滤为全透水，则每个测点的水平方向几乎是最短渗径．

因此，可以近似认为超静孔隙水压力形成的渗流场的渗径接近水平．即心墙在竖向承受荷载，孔隙水主要沿水平方向向上、下游两侧渗透系数较大的反滤料排出．也就是心墙超静孔隙水压力是竖向承压水平排水的单向固结问题．

3.1 基本假定

大坝心墙在自重作用下超静孔隙水压力消散问题基本符合太沙基单向固结理论的基本假定．只不过太沙基单向固结的承压方向与渗流方向一致，而大坝心墙的超静孔隙水压力消散问题的承压方向与渗流方向垂直．需要特别说明的是，由于坝体心墙体积庞大，上部土体和底部土体的应力条件差别巨大，其渗透系数和压缩系数自然因高程而异．但同一高程上，同一测点心墙在竣工期间的外部条件变化不大，可以近似认为其渗透系数和压缩系数为常数．特别是研究同一观测高程心墙在某一时间段内的超静孔隙水压力消散问题时，认为心墙的渗透系数和压缩系数为常数是可以接受的．

3.2 微分方程的建立与求解

在心墙中深度z处取一断面积为1×1，厚度为dx的微元体，如图4所示．

图4 一维渗流固结过程

该微元体固体体积为

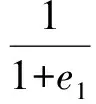
(1)

孔隙体积为

(2)

式中：e1表示固结前土的孔隙比．

在dt时间内，微元体中孔隙体积的变化等于同一时间内从微元体中流出的水量，即

(3)

式中：q表示单位时间内流过单位横截面积的水量．

将式(2)、(3)联立，得

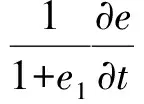
(4)

由土的压缩系数公式和饱和土体有效应力原理可得

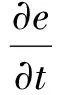
(5)

式中：a表示土的压缩系数；∂σ′z表示粒间有效应力；u表示孔隙水压力．

达西定律：

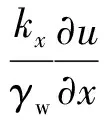
(6)

将式(5)、(6)代入式(4)得

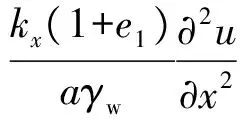
(7)

定义土的固结系数为

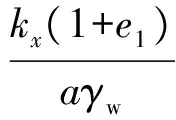
(8)

式中：kx为水平渗透系数，cm/s；a为压缩系数，kPa-1．

得一维固结微分方程

(9)

求解该微分方程的初始条件和边界条件如下：

初始条件

t=0，0≤x≤l，u=u0=φ(x)

(10)

边界条件

00t=∞,0≤z≤H，u=0

(11)

由分离变量法可求得该问题的解为

(12)

式中，叠加系数

(13)

对于心墙内的某一点A，其初始孔隙水压力为已知的某一值p，其叠加系数可由式(13)求得，即

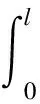
(14)

心墙内某一点孔隙水压力消散问题的解答为

(15)

4 竖向受压水平排水固结方程的应用

为了验证心墙一维固结计算公式的合理性，进行孔压消散计算值与实测值的拟合．选择孔压消散计算的起始时间为2012-07-01(心墙填筑至807.68 m)，此时进入雨季，心墙暂停填筑，心墙内测点孔隙水压力达到填筑期的最大值．直至2012-09-23重新开始填筑，2012-12-18填筑至坝顶．选取心墙填筑完成且库水位保持相对稳定时段(2012-12-18～2013-07-08)测点的实测数据与一维固结计算值进行对比．

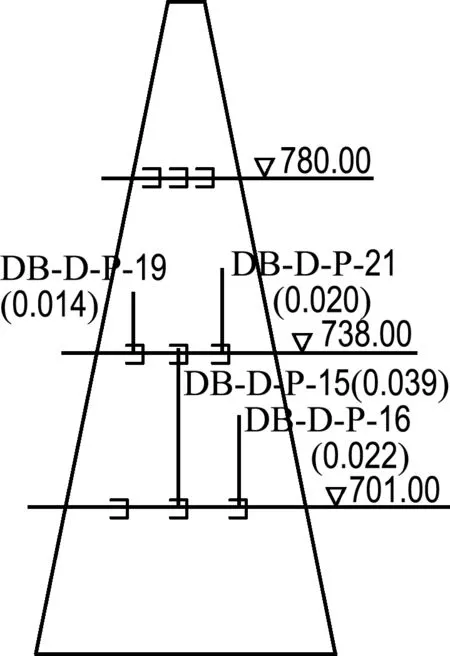
由式(8)可知，固结系数与kx、e1和a有关．本文在基本假定中已经说明同一观测点在选取的某一时间段内渗透系数、压缩系数可近似视为常数，即同一观测点在某个固结过程中的固结系数视为常数．已知心墙填筑压实后的孔隙比为0.33，根据掺砾心墙土料固结试验成果可知，孔隙比为0.30～0.36的处于饱和状态的掺砾料的固结系数范围为0.011～0.040 cm2/s．本文在该范围内取合适的固结系数，使得孔压实测值与一维固结计算值拟合得更好．布置有渗压计的3个断面A-A(0+169.36)、C-C(0+309.60)和D-D(0+482.30) 中有15个测点观测数据有效，进行一维固结计算所需参数l和x见表1，不同测点固结系数取值如图5所示(柱状图旁括弧内的数值为固结系数，单位为cm2/s)，测点孔压实测值与一维固结计算值拟合情况如图6～8所示．

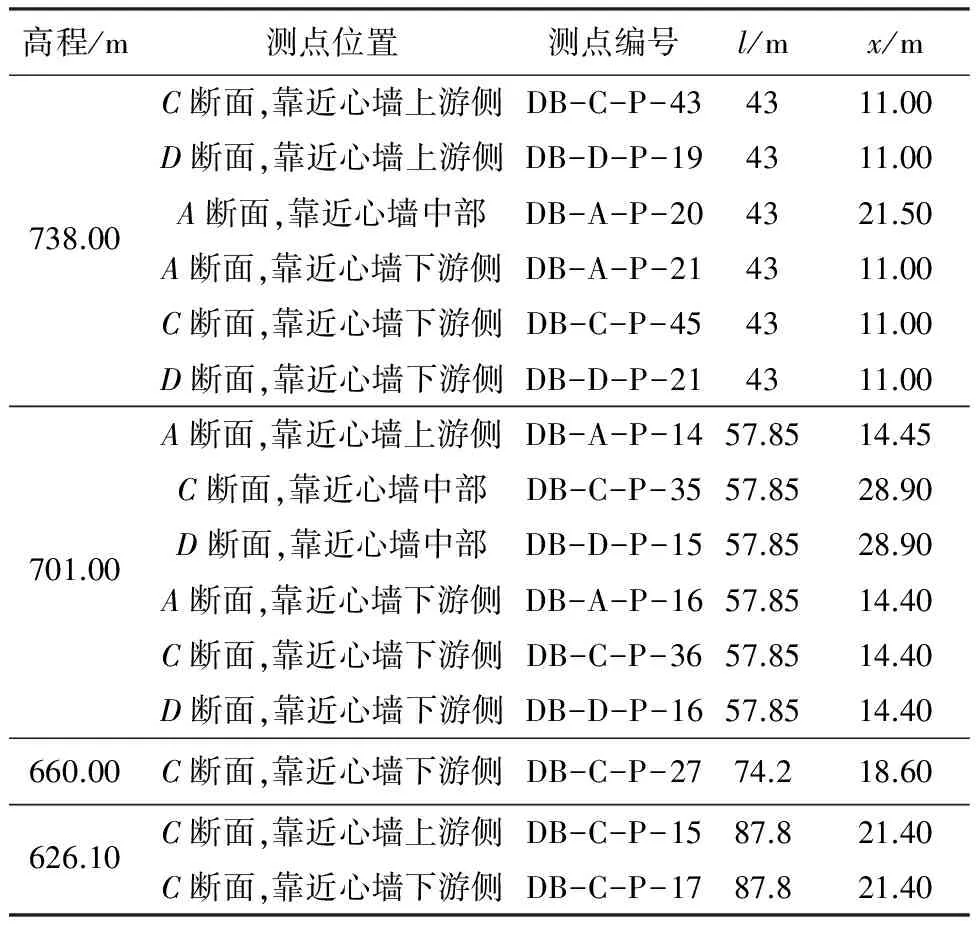
表1 参数统计表

由图5可知，心墙内15个渗压计测点的固结系数取值均在孔隙比为0.30～0.36(心墙填筑压实后的孔隙比平均值为0.33)的处于饱和状态掺砾料固结试验成果范围内，即0.011～0.040 cm2/s，从试验的角度讲，所取的固结系数是合理的．固结系数的分布总体为不同断面同一高程心墙中部固结系数>心墙下游侧固结系数>心墙上游侧固结系数，这主要是由于大坝竣工蓄水后心墙大主应力分布特征为心墙中部最大，距心墙中部相等距离的下游测点大于上游测点，而大主应力越大，心墙压得越密实，与固结系数相关的a、kx和e1越小，但压缩系数a相对渗透系数kx和初始孔隙比e1的变化更大，最终导致大主应力大的地方固结系数大．

由图6～8可知，测点渗压计水头计算值与实测值最大绝对误差均小于2 m．相对误差(相对误差=绝对误差/(坝顶高程-最低建基面高程)×100%)最大值出现在测点DB-A-P-20，该点绝对

(a) C-C断面(0+309.60)

(b)A-A断面(0+169.36)

(c)D-D断面(0+482.30)

图5 心墙测点固结系数柱状图

Fig.5 Bar chart of consolidation coefficient in core-wall

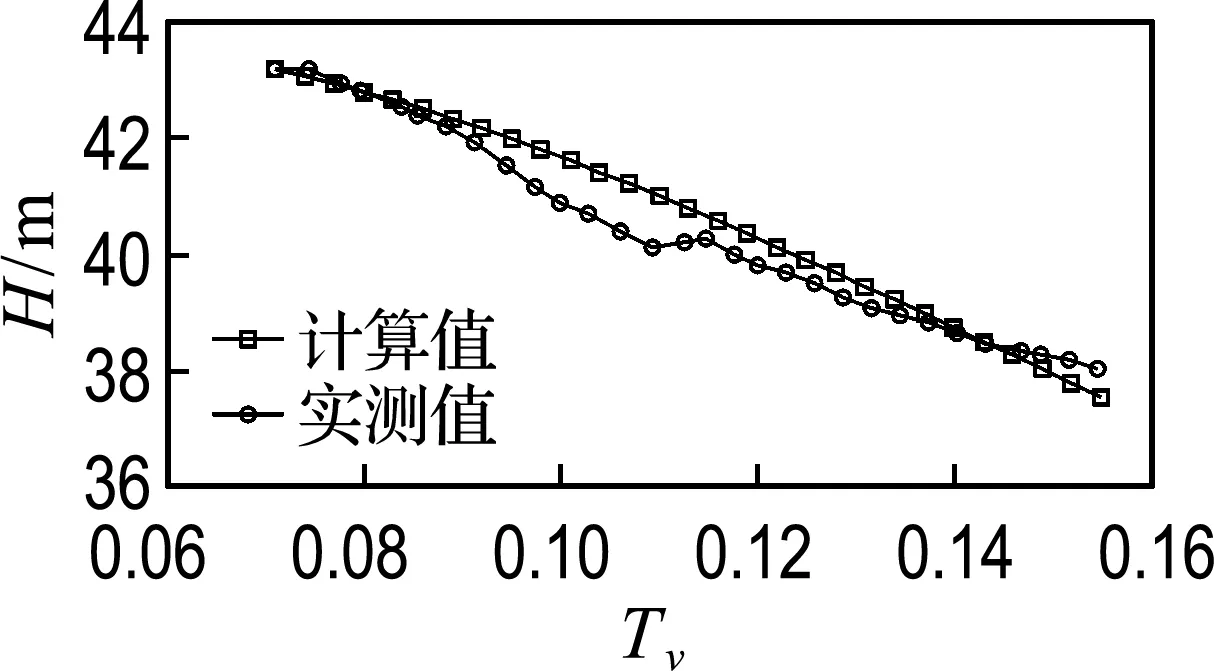
(a) DB-A-P-20 (A断面，心墙中部)

(b) DB-D-P-19 (D断面，心墙上游侧)

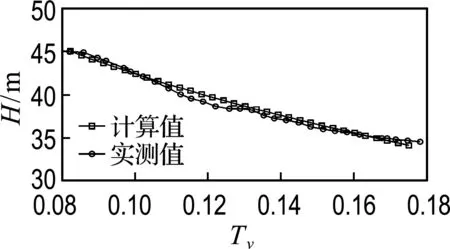
(c) DB-C-P-45 (C断面，心墙下游侧)

图6 738.00 m高程心墙渗压计水头计算值与实测值对比

Fig.6 Comparison between measured and simulated hydraulic heads of osmometers at 738.00 m elevation in core-wall

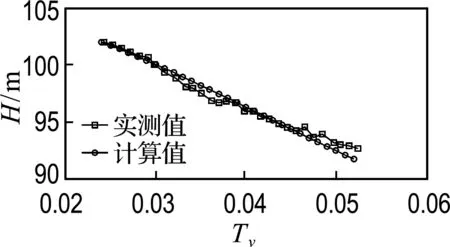
(a) DB-A-P-14 (A断面，心墙上游侧)

(b) DB-D-P-15 (D断面，心墙中部)

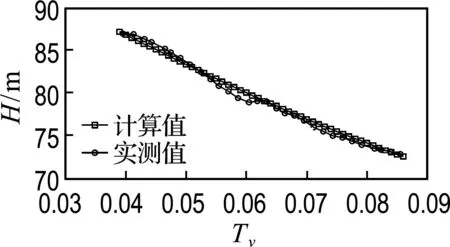
(c) DB-C-P-36 (C断面，心墙下游侧)

图7 701.00 m高程心墙渗压计水头计算值与实测值对比

Fig.7 Comparison between measured and simulated hydraulic heads of osmometers at 701.00 m elevation in core-wall

(a) DB-C-P-15 (C断面，心墙上游侧)

(b) DB-C-P-17 (C断面，心墙下游侧)

图8 626.10 m高程心墙渗压计水头计算值与实测值对比

Fig.8 Comparison between measured and simulated hydraulic heads of osmometers at 626.10 m elevation in core-wall

误差最大值约为1.9 m，所处断面最低建基面高程为642.00 m，求得相对误差为1.1%．较好的拟合结果说明将大坝心墙填筑完成后孔隙水压力消散问题简化为一维固结问题是可行的，文中将实测数据与一维固结计算值进行拟合时所取的固结系数是合理的．

5 孔隙水压力消散时间

经某一时间t后，土体内孔隙水压力消散的程度称为固结度．对某一深度z处经过时间t后，测点的固结度U可用下式表示：

(16)

式中：p表示测点的初始孔隙水压力；u表示t时刻该点的孔隙水压力．

将式(15)代入式(16)，可得到

(17)

由表1及图5给出的各测点l、x和Cν的取值，以各高程不同位置的8个测点为例，将各测点的固结度U与时间t的关系绘制成曲线，如图9所示．

图9 固结度与时间关系曲线

由图9可知，固结初期，相同高程位于心墙中部的测点因距排水边界较远，固结速率较距排水边界近的测点慢．固结时间t=10 a的时间段内，各测点的固结度达到了70%～95%．当固结度U≥95%后，不同测点的固结速率均趋于很小(接近零)，各测点固结度与时间的关系曲线趋于重合．该现象可从式(16)得到解释，即当U→100%时，t→+∞．本文近似认为当测点的固结度达到95%后，测点的固结基本完成．将3个断面不同测点固结度达到95%所需的时间列于表2．

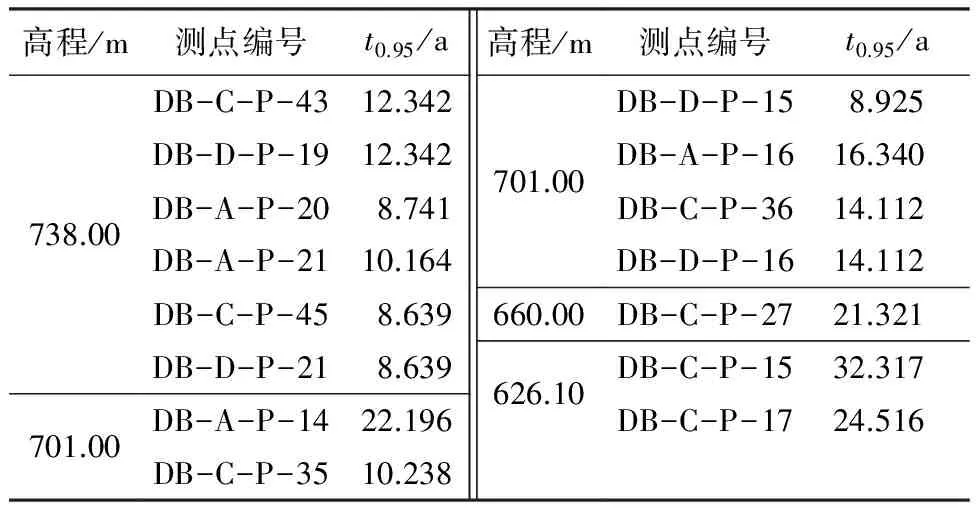
表2 固结度95%各测点所需固结时间

由表2可知，在不考虑上游库水位影响的情况下，不同高程测点固结度达到95%所需的时间：738.00 m高程测点所需时间平均为10.14 a，701.00 m高程测点所需时间平均为12.99 a，660.00 m高程测点所需时间为21.32 a，626.10 m高程测点所需时间平均为28.42 a．可见，由心墙填筑引起的超静孔隙水压力消散所需时间长达10～30 a．但在大坝填筑完成的前2 a内，心墙内的超静孔隙水压力较高，会导致其有效应力降低及易产生水力劈裂，应引起足够的重视．

6 结 论

(1)心墙填筑期，渗压计埋设后很快便能测得孔隙水压力，几乎没有滞后性，说明心墙料填筑时接近饱和；超静孔隙水压力随心墙填筑而增大，且增大速率与心墙的填筑速率有良好的相关性，当心墙填筑慢或在雨季暂停填筑时，超静孔隙水压力增长慢并趋于零增长甚至逐渐消散；心墙填筑完成时，测点高程越低，(超静)孔隙水压力水头值越高；相同高程不同位置测点的孔隙水压力，心墙上游侧>心墙中部>心墙下游侧．

(2)心墙内15个渗压计测点的固结系数取值范围为0.014～0.039 cm2/s，从固结试验的角度讲，所取的固结系数是合理的；固结系数的分布大体呈现不同断面同一高程心墙中部固结系数>心墙下游侧固结系数>心墙上游侧固结系数的规律．

(3)3个断面15个测点渗压计水头计算值与实测值最大绝对误差均小于2 m，相对误差最大值为1.1%．较好的拟合结果说明将大坝心墙填筑完成后的孔隙水压力消散问题简化为一维固结问题是可行的，测点所取的固结系数是合理的．

(4) 由心墙填筑引起的超静孔隙水压力消散所需时间长达10～30 a，尤其在大坝填筑完成的前一两年内，心墙内超静孔隙水压力较高，会导致其有效应力降低及易产生水力劈裂，应引起足够的重视．

[1] 中华人民共和国行业标准编写组. 碾压式土石坝设计规范: DL/T 5395—2007 [S]. 北京:中国电力出版社, 2008.

The Professional Standards Compilation Group of People′s Republic of China. Design Specification for Rolled Earth-rock Fill Dams: DL/T 5395-2007 [S]. Beijing: China Electric Power Press, 2008. (in Chinese)

[2] 王柏乐. 中国当代土石坝工程[M]. 北京:中国水利水电出版社, 2004:1-2.

WANG Baile.ChineseContemporaryEarthandRockfillDam[M]. Beijing: China Water Power Press, 2004:1-2. (in Chinese)

[3] 屈智炯. 宽级配砾质土在土石坝防渗体中的应用及渗流控制的进展[J]. 水电站设计, 1992,8(3):46-53.

QU Zhijiong. Application of wide grading gravelly soil in the embankment dam seepage and progress of seepage control [J].DesignofHydroelectricPowerStation, 1992,8(3):46-53. (in Chinese)

[4] 陈继平,曹林曦,刘明华,等. 砾石土心墙堆石坝施工期孔隙水压力分析[J]. 岩土力学, 2008,29(z1):176-180.

CHEN Jiping, CAO Linxi, LIU Minghua,etal. Pore water pressure analysis during construction of gravelly soil corewall rockfill dam [J].RockandSoilMechanics, 2008,29(z1):176-180. (in Chinese)

[5] 陈立宏,陈祖煜,张进平,等. 小浪底大坝心墙中高孔隙水压力的研究[J]. 水利学报, 2005,36(2):219-224.

CHEN Lihong, CHEN Zuyu, ZHANG Jinping,etal. Study on high pore pressure in clay core wall of earth dam in Xiaolangdi Project [J].JournalofHydraulicEngineering, 2005,36(2):219-224. (in Chinese)

[6] 郑 俊,邓建辉,杨晓娟,等. 瀑布沟堆石坝砾石土心墙施工期孔隙水压力特征与分析[J]. 岩石力学与工程学报, 2011,30(4):709-717.

ZHENG Jun, DENG Jianhui, YANG Xiaojuan,etal. Characteristics and analysis of pore water pressure in gravelly soil corewall of Pubugou rockfill dam during construction period [J].ChineseJournalofRockMechanicsandEngineering, 2011,30(4):709-717. (in Chinese)

[7] 张宗亮. 糯扎渡水电站工程特点及关键技术研究[J]. 水力发电, 2005,31(5):4-7.

ZHANG Zongliang. The project characteristics of Nuozhadu Hydropower Station and its key technology research results [J].WaterPower, 2005,31(5):4-7. (in Chinese)

[8] 袁友仁,张宗亮,冯业林,等. 糯扎渡心墙堆石坝设计[J]. 水力发电, 2012,38(9):27-30.

YUAN Youren, ZHANG Zongliang, FENG Yelin,etal. Design of Nuozhadu core rockfill dam [J].WaterPower, 2012,38(9):27-30. (in Chinese)

[9] 李广信. 高等土力学[M]. 北京:清华大学出版社, 2011.

LI Guangxin.AdvancedSoilMechanics[M]. Beijing: Tsinghua University Press, 2011. (in Chinese)

Analysisofporewaterpressureingravellysoilcore-wallofrock-filldam

NIShasha,CHIShichun*

(SchoolofHydraulicEngineering,FacultyofInfrastructureEngineering,DalianUniversityofTechnology,Dalian116024,China)

High excess static pore water pressure will rise in the core-wall of earth dam during the rolling construction period. For the high earth dam, the excess static pore water pressure produced in the core-wall of earth dam during construction can not be effectively dissipated, and the existing high pore water pressure will lead to the reduction of effective pressure in the core-wall, which influences the performance of core-wall and stability of the dam. Based on the monitoring data of a gravelly soil core-wall, the influences of core-wall filling building and reservoir storage on the pore water pressure formation and variation are analyzed. The calculation of pore water pressure dissipation in the core-wall is simplified to one-dimensional consolidation method of vertical compression and horizontal drainage, and it is applied to the calculation of pore water pressure dissipation in the core-wall under the condition that the core-wall filling building is completed and reservoir water level keeps constant. The reasonability of simplifying calculation is verified through the comparison of the tested and calculated data. It is found through the consolidation process of the core-wall that it will take 10 to 30 years when the degree of consolidation achieves 95%, and at each monitoring point achieves 70% at 10 years.

gravelly soil core-wall; pore water pressure; monitoring; one-dimensional consolidation; degree of consolidation

1000-8608(2017)06-0593-08

TU443

A

10.7511/dllgxb201706007

2016-10-10；

2017-07-17．

国家自然科学基金资助项目(51379029).

倪沙沙(1985-)，女，博士生，E-mail:548899337@qq.com；迟世春*(1964-)，男，教授，E-mail:schchi@dlut.edu.cn.